伪目标迭代生成的机器人误差补偿算法

叶伯生 金雄程 黎晗 邵柏岩 李晓昆 李思澳

摘要：针对机器人误差模型建立后的误差补偿问题，提出一种改进的伪目标迭代算法。该算法用每次迭代中生成新的伪目标来修正关节角，从而不断减小机器人实际误差。完善了伪目标迭代算法流程，提出了5种新的不同的伪目标生成方法，分析了各种方法的特点和适用场景。结合多种伪目标生成方法提出了一种集成算法，进一步提高误差补偿精度。使用HSR-JR612机器人进行仿真实验，仿真结果表明，算法耗时在毫秒级别，补偿效果好，集成算法能进一步提高位姿补偿效果。最后使用UR10机器人与激光跟踪仪进行实验，实验结果表明，补偿后机器人末端位置误差可以减小到0.06 mm以内，姿态误差可以减小到0.025°以内。

关键词：机器人；误差补偿；定位精度；伪目标

中图分类号：TP242.2

DOI：10.3969/j.issn.1004132X.2024.01.013

Robot Error Compensation Algorithm by Pseudo Target Iterative Generation

YE Bosheng JIN Xiongcheng LI Han SHAO Baiyan LI Xiaokun LI Siao

School of Mechanical Science and Engineering，Huazhong University of Science and Technology，

Wuhan，430074

Abstract： Aiming at the problems of error compensation after robot error modeling， an improved algorithm was proposed based on pseudo target iteration. This algorithm generated a new pseudo target in each iteration to correct the joint angles， thereby continuously reducing the actual errors of the robot. The pseudo target iterative algorithmic process was improved to mature the algorithm flow， 5 new and different false target generation methods were proposed， and the characteristics and applicable scenarios of each method were analyzed. An ensemble algorithm was proposed combining multiple false target generation methods to further improve the accuracy of error compensation. Using the HSR-JR612 robot to carry out simulation experiments， the simulation results show that the algorithm takes milliseconds and the compensation effectiveness is good， and the integrated algorithm may further improve the pose compensation effect. Finally， the UR10 robot and the laser tracker were used for experiments. The experimental results show that after compensation， the position errors of the robot end may be reduced to less than 0.06 mm， and the attitude errors may be reduced to less than 0.025°.

Key words： robot； error compensation； positioning accuracy； pseudo target

0 引言

工業机器人末端位置误差主要分为几何参数误差和非几何参数误差［1］，几何参数包括关节角、连杆长度、连杆偏置等［2］，可以先进行几何参数辨识，再直接修正控制器内部的对应参数来补偿几何参数误差。ZENG等［3］和CHEN等［4］在计算合理的位置误差后，直接修改机器人控制命令中的位置坐标来实现补偿。但是许多机器人的控制器没有开放底层修改权限，而且非几何参数误差不能通过直接修改控制器参数来补偿。

为了提高机器人末端精度，需要准确的补偿技术对辨识出来的误差进行补偿。ANGELIDIS等［5］设计了一种能够直接预测指令位置的神经网络，在此指令位置下机器人实际输出的位置接近期望位置。但这类算法没有直接计算实际误差然后补偿，对数据集的依赖性大，即数据采集成本高。倪华康等［6］采用微分误差补偿法来补偿几何参数误差和基坐标系误差造成的末端误差。此类方法较为常用，但这种方法只进行一次补偿，补偿效果有进一步的提高空间。陈宵燕［7］基于误差模型提出了一种笛卡儿空间摄动补偿算法，原理是基于最小二乘法最小化残余误差，补偿效果较好，但算法运算量大。何庆稀等［8］将激光跟踪仪测出的位姿偏差直接附加到指令位姿实现在线位姿补偿，此类方法原理简单但补偿精度有限。预测补偿法是一种输入运动规划法［9］，能将笛卡儿空间的位置误差映射到关节空间中，通过修正关节角来实现末端误差补偿。NGUYEN等［10］使用逆雅可比矩阵将位置误差转换为关节角补偿值，但可能存在矩阵奇异性问题。奚陶［11］基于Newton-Raphson法根据末端位置误差来修正关节角。DEVLIEG等［12］提出采用关节空间补偿法对关节间隙引起的位置误差进行在线补偿。上述几种预测补偿算法补偿精度高，但没有对算法耗时进行具体的量化讨论。尹仕斌［13］提出了一种基于伪目标位姿迭代的算法来补偿实际输入的关节角，该算法每个位置点的平均迭代次数在3～5次，效率较高。

针对建立误差辨识模型后的误差补偿环节，本文提出一种改进的基于伪目标迭代的误差补偿算法，通过修正关节角实现位置或位姿的误差补偿。关于算法中的逆运动学，提出使用数值迭代法来代替解析法，另外提出5种新的伪目标生成方法，并综合多种生成方式来提高补偿精度。最后使用HSR-JR612机器人进行仿真实验，验证算法的有效性。

1 误差补偿算法介绍

如果不考虑机器人实际存在的几何误差及非几何误差，在每次作业中，机器人会通过逆运动学由目标位姿Td（相对于机器人基坐标系）得到机器人的理论输入关节角θd，并将其输入控制器，二者关系如下：

θd=IK（Td）（1）

其中，目标位姿Td∈SE（3），SE（3）表示三维特殊欧氏群（special Euclidean group），IK（·）为机器人的逆运动学函数。本文的讨论对象是六自由度关节机器人，因此关节角向量θd∈R6。

实际上机器人受几何误差、关节柔性误差等各种因素影响，其末端存在一定的误差，为此，需要准确的误差辨识模型（或称误差预测模型）去预测不同关节角下的末端误差。本文的算法根据预测或测量得到的误差，对输入关节角进行修正，得到修正的关节角θa，使得实际机器人末端位置在关节角为θa时尽可能地逼近目标位置。

建立误差辨识模型后，将预测实际末端位姿的函数（actual pose predictor）设为AP（θ），输入为一组关节角，输出为预测的实际末端位姿。该函数可针对不同机器人选用准确的误差预测模型进行实现，比如可以使用分级误差预测模型［2，10］或其他误差预测模型［5］。

將修正关节角度θa通过理论正运动学得到的位姿定义为伪目标（pseudo target，PT）位姿点Tp。算法的最终目的是使该修正关节角θa对应的实际末端位姿Ta逼近目标位姿Td。综上，有如下关系成立：

Tp=FK（θa）（2）

θa=IK（Tp）（3）

Ta=AP（θa）（4）

其中，FK（·）为机器人理想模型的正运动学函数，修正关节角θa∈R6，位姿Ta、Tp均属于SE（3）。

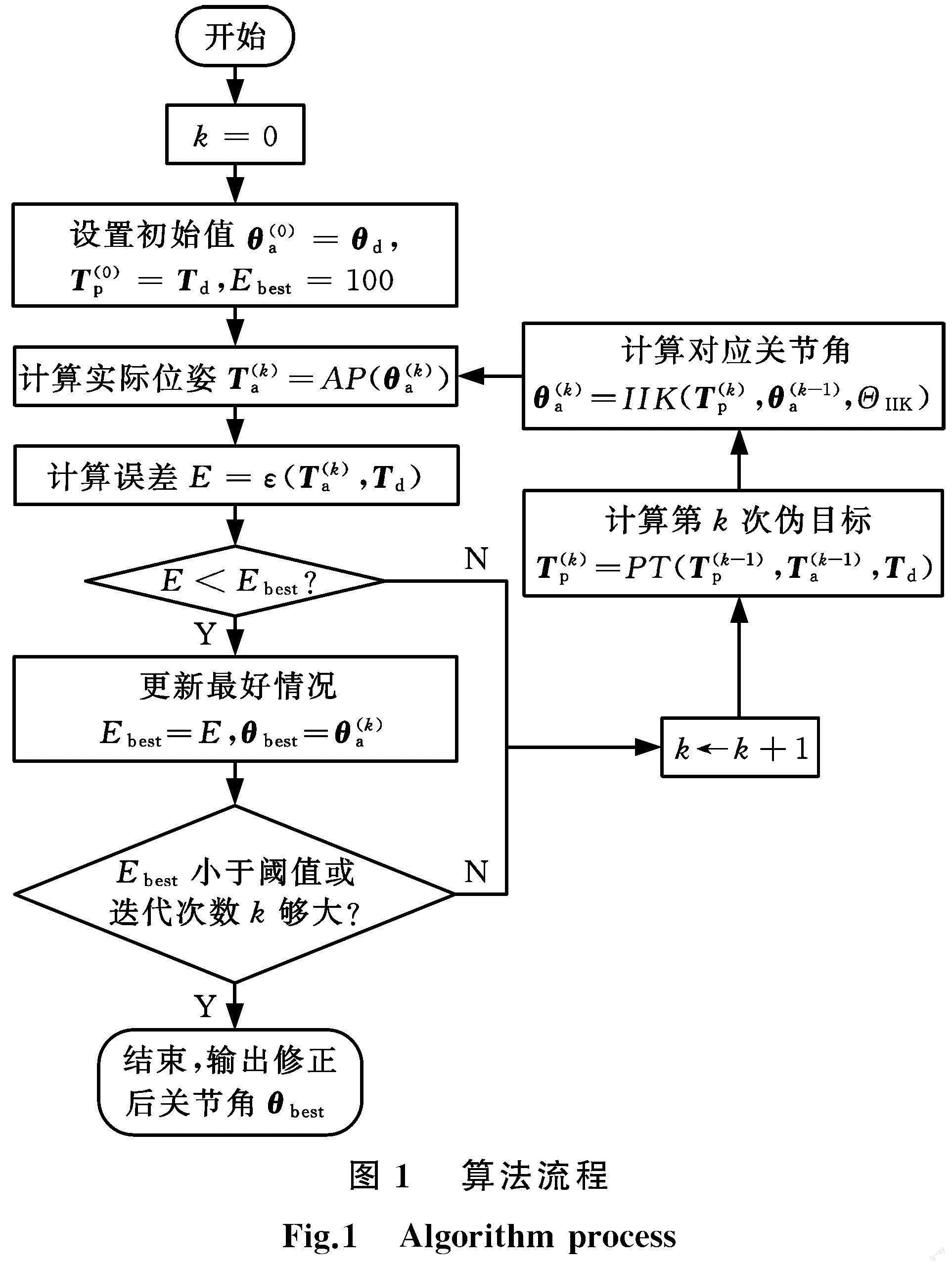
基于文献［13］提出的“伪目标位姿”迭代补偿算法，本文进一步拓展和改进，采用不同的逆运动学函数，提出多种新的伪目标生成方式。改进的伪目标生成迭代算法主要流程如图1所示。

主要过程描述如下：

（1）迭代开始。迭代次数k=0，将修正关节角的初始值θ（0）a设为θd，将初始伪目标T（0）p设为目标位姿Td，二者关系如式（1）所示。设置变量Ebest来记录最小的末端误差，变量θbest记录最小误差对应的修正关节角，Ebest的初始值设为一个较大数即可，如图1中将其设为100。

（2）根据式（4）计算θ（k）a对应的末端实际位姿：

T（k）a=AP（θ（k）a）（5）

（3）计算第k次迭代中θ（k）a对应的末端实际位姿及其与目标位姿Td间的误差：

E=ε（T（k）a，Td）（6）

式中，函数ε（·）用来计算两个位姿之间的误差，根据不同的需求，可以用不同的误差计算函数。

当只关心末端位置精度时，误差计算可以使用下式所示的笛卡儿空间位置误差公式：

式中，P（k）ax、P（k）ay、P（k）az为T（k）a在3个笛卡儿坐标轴上的位置分量；Pdx、Pdy、Pdz为Td在3个笛卡儿坐标轴上的位置分量。

同时考虑位置精度和姿态精度时，误差计算可以采用文献［13-14］中所使用的位姿误差计算公式：

其中，E的计算结果单位为mm，xe、ye、ze、r（1）e1、r（2）e2、r（3）e3由下式求得：

（4）计算误差E后，若E＜Ebest，则更新Ebest和θbest；否则继续迭代，更新迭代次数k←k+1。若更新了Ebest，同时Ebest小于阈值或迭代次数k大于预设值，则停止迭代，输出θbest作为最终修正关节角输出；否则继续迭代，更新迭代次数k←k+1。

（5）根据上一次迭代生成第k（k>0）次迭代的伪目标位姿：

T（k）p=PT（T（k－1）p，T（k－1）a，Td）（10）

式中，PT（·）为伪目标生成函数。

（6）通过迭代逆运动学（iterative inverse kinematics，IIK）算法计算伪目标对应的关节角：

θ（k）a=IIK（T（k）p，θ（k－1）a，ΘIIK）（11）

其中，IIK（·）为迭代法逆运动学函数，这类算法除了要输入姿态，一般还需要输入一组关节角初值和标志迭代结束的误差阈值；ΘIIK为标志迭代结束的误差阈值。

如式（11）所示，迭代逆运动学将上一个伪目标对应的关节角θ（k－1）a作为迭代初始值，由于每次生成的伪目标和上一次迭代生成的伪目标比较接近，所以选用该初值能够提高逆运动学算法效率，同时保证算法稳定性。经过比较，本文以及后续的仿真中将使用文献［15］中的迭代算法，该算法在迭代后期有较好的稳定性。

（7）返回步骤（2）并重复之后的步骤。

2 多种伪目标生成方式

伪目标生成的原则为：伪目标加上其对应误差后的末端实际位姿能够逼近目标位姿Td，下面将讨论式（10）中伪目标生成函数PT（·）的具体实现。文献［13］提出的伪目标生成函数已经被验证有较好的补偿效果，其具体实现如下式所示：

T（k）p=T（k－1）p（T（k－1）a）－1Td（12）

由于算法思想是类似的，因此伪目标生成方式的流程应该为：参考目标位姿Td和实际位姿T（k－1）a间的偏差，在上一个伪目标位姿T（k－1）p的基础上生成下一个伪目标。机器人末端位姿可以表示为

其中，姿态部分R∈SO（3），SO（3）为三维特殊正交群（special orthogonal group），位置部分P∈R3。

在伪目标生成方法中，本文将位置和姿态分别进行处理。

2.1 位置部分生成方法

伪目标生成的重点在于找到合适的方法去衡量伪目标位姿与目标位姿间的偏差，并靠生成新的伪目标来补偿这个偏差，其中位置部分的差距使用坐标相减的差来衡量。本文提出的伪目标生成算法中，位置部分均采用下式进行计算：

P（k）p=P（k－1）p－ΔP=P（k－1）p－（P（k－1）a－Pd）=

P（k－1）p+Pd－P（k－1）a（14）

其中，P（k）p为第k次迭代生成的伪目标的位置，P（k－1）a为上一次迭代中关节角θ（k－1）a对应的实际位置，Pd为目标位置。三者均属于R3。

2.2 姿态部分生成方法

伪目标生成算法的姿态部分可采用多种方式处理，本文将对比讨论这几种方法。下文提到的R（k）p表示第k次生成的伪目标的姿态，R（k－1）a为第k－1次迭代中关节角对应的实际位置，Rd为目标位姿的姿态部分，三者均属于SO（3）。

（1）固定姿态法。若只考虑位置误差而不关心姿态误差，则可以一直选择目标姿态Rd作为伪目标的姿态，即选择如下策略更新伪目标的姿态部分：

R（k）p=Rd（15）

式（15）的优点在于运算量小，效率高，缺点在于没有考虑位姿部分的误差，最终可能会出现末端位置误差小但姿态误差大的补偿结果，所以不适用于对位姿精度要求高的情况。

（2）直接加減法。将姿态误差定义为相减，通过加减来实现伪目标更新，此时更新策略如下：

R（k）p=R（k－1）p+Rd－R（k－1）a（16）

式（16）明显的缺点在于不能保证R（k）p∈SO（3），所以生成的伪目标不一定是有效的姿态矩阵，在逆运动学求解时可能会无解。但本文提出使用的迭代逆运动学属于数值求解法，能在一定程度上缓解这种情况，只要设置合适的迭代结束阈值ΘIIK，也能够使整体算法迭代收敛，并使结果有效。式（16）的优点在于运算简单，相比于固定姿态法多考虑了姿态误差，理论上能够进一于步提高姿态精度。

（3）直接相乘法。为了保证生成的伪目标的姿态R（k）p∈SO（3），定义如下的姿态更新策略：

R（k）p=Rd（R（k－1）a）－1R（k－1）p=Rd（R（k－1）a）TR（k－1）p（17）

文献［13］提出的式（12）中的矩阵相乘需要进行128次实数乘法，而式（17）与式（14）总共只需54次实数乘法，同时基于SO（3）的性质，矩阵逆运算转变成了运算简单的矩阵转置运算，所以直接相乘法理论上有更高的运算效率。

（4）三角度转换法。机器人轨迹插补领域中有一种经典方法是先将姿态转换成三角度表示法（如欧拉角形式、导航角形式）进行处理，再将姿态转换回SO（3）的形式。所以可以考虑在欧拉角空间或导航角空间进行如同式（16）的操作，更新策略如下：

R（k）p=EtoR（RtoE（R（k－1）p）+RtoE（Rd）－RtoE（R（k－1）a））（18）

其中，EtoR（·）是将姿态从SO（3）形式转换为三角度表示法形式的变换函数，RtoE（·）是其逆变换，可调用现有的相关函数实现。

三角度表示法可以采用Z-Y-Z序列形式（即欧拉角形式），也可采用X-Y-Z序列形式（即导航角形式）。三角度转换法提出了一种新的处理角度方法，但缺点是这类姿态表示方法可能存在万向节死锁问题，虽然是极少数情况，但这可能会导致算法无法求解。

（5）单位四元数转换法。姿态还可以使用单位四元数（unit quaternion）描述，四元数不存在万向节死锁问题，同时四元数、SO（3）矩阵和欧拉角之间能进行无信息损失转换［16-17］。一个单位四元数q满足：q∈Q且其模|q|=1，其中，Q为四元数集合。

在本方法中，首先将姿态R（k）p、R（k－1）a、Rd转换为对应的单位四元数形式q（k）p、q（k－1）a、qd，可以使用文献［16］中的方法或直接调用相关函数实现。根据单位四元数性质，得到如下更新伪目标公式：

q（k）p=q（k－1）p（q－1dq（k－1）a）－1=q（k－1）p（q（k－1）a）*qd（19）

式中，（q（k－1）p）*表示q（k－1）p的共轭四元数，共轭运算即四元数所有虚部取反。

最后需要将q（k）p转换为SO（3）形式。本方法的创新在于效仿了球面线性插补（spherical linear interpolation）算法［17］的思想，提出在单位四元数空间中生成伪目标的姿态，优点在于没有万向节死锁问题，缺点是有两次形式转换的过程，运算成本会稍微高一些。

3 多算法集成

基于上述多种伪目标生成算法以及文献［13］的算法，结合其各自的优缺点，本文提出对多个算法进行集成使用的思路，即对于某个待补偿的目标点，使用多个算法求解补偿后的关节角，最后对比各自的补偿效果，选择效果最好的关节角作为最终输出关节角，流程如图2所示。

考虑到不同生成算法对不同目标点的误差补偿效果不同，采用这种有效的策略可发挥各个生成算法的优势。

4 算法验证

4.1 仿真验证

本节将使用HSR-JR612机器人及文献［2］中的误差模型进行仿真实验，通过补偿仿真出来的误差来验证所述算法的有效性，并计算各个算法的耗时。机器人运动学模型的D-H参数如表1所示。

机器人通过D-H建模得到的正运动学模型用f（a，d，α，θ）来表示，其中，a为包含各连杆长度的向量，d为包含各连杆偏置的向量，α为包含各连杆扭曲的向量，θ为各关节角角度向量。上述变量均属于R6。

参考文献［2］，本次仿真实验中主要对几何参数误差以及受机器人自重等影响造成的关节柔性误差进行仿真。此时式（5）中计算实际位姿的AP（·）函数应该是根据正运动学模型进行修正后得到的模型，可以表示为

AP（θ）=f（a+Δa，d+Δd，α+Δα，θ+Δθ+δθ）（20）

δθ=（δθ1，δθ2，δθ3，δθ4，δθ5，δθ6）T

式中，Δa、Δd、Δα、Δθ为机械臂的几何参数误差；δθ为关节柔性误差，即机械臂自重等原因造成的额外关节角误差。

本次仿真中，机器人几何参数误差的取值如表2所示。

关节柔性误差主要考虑受机械臂自重影响明显的关节2和关节3，其他柔性误差视为0，即δθ1=δθ4=δθ5=δθ6=0。δθ2和δθ3的计算如下式所示：

δθ2=k1sin θ2+k2sin（θ2+θ3）+k3cos（θ2+θ3）（21）

δθ3=k4sin（θ2+θ3）+k5cos（θ2+θ3）（22）

其中，θi（i=1，2，…，6）为第i个关节的关节角；本次仿真中其他常数选取较小值k1=1×10－3，k2=k3=k4=k5=5×10－4。

伪目标生成算法的迭代过程中误差计算函数使用式（7），该公式用于计算末端位置误差，表示优先以最小化位置误差为补偿目标。本文还将计算位姿误差来方便对比，位姿误差使用式（8）进行计算。

逆运动学函数IIK（·）选用文献［15］中改进的Levenberg-Marquardt（LM）算法，该逆运动学算法需要如下几个参数：标志迭代结束的阈值参数ΘIIK、最大迭代次数、防止计算过程中雅可比矩阵出现奇异值的极小偏置值ω-N。本次仿真中的相关参数取值和关节角数据采集范围选取如表3所示。

在关节角范围内随机选取1000组关节角，使用本文算法求解修正后的关节角，并记录对应的误差，结果如表4所示。

结果表明，本文提出的算法均能够有效地通过修正关节角来补偿位置误差，并且耗时短，算法效率高。其中，值得注意的是：

（1）固定姿态法的耗时最短，因为其运算量最小，同时该算法的位置误差补偿效果也最好。不足之处在于位姿误差的补偿效果相对较差。

（2）其他方法的补偿效果和耗时都相近。由于欧拉角法和导航角法有两次转换过程，故耗时相对较长。考虑到第2节关于直接加减法、三角度法的局限性分析，建议优先使用直接相乘法和单位四元数法这两种方法。

（3）虽然几种方法的误差补偿效果的整体平均值相近，但各种方法在各个位置点上的补偿效果并不相同，所以为了发挥各种方法的补偿优势，需要考虑使用集成算法。

现比较文献［13］方法、单位四元数法以及综合以上两种方法的集成算法三者的补偿效果，结果如图3所示。

经过统计，集成算法在1000组修正关节角的选择中，有521组选用的是单位四元数的修正结果。结果表明，集成算法能非常有效地提高位姿误差补偿效果，所以在需要位姿补偿的场景可以优先考虑使用集成算法。

为了验证本文算法的轨迹修正效果，在工作空间内指定一条如图4所示的圆周轨迹，末端姿态是固定值，轨迹规划使用梯形速度法，共使用2000个采样点。

首先对期望轨迹上每个末端点进行逆运动学运算，得到一组关节角序列，并将其代入式（20）得到修正前的轨迹；然后使用基于直接相乘法和单位四元数法的集成算法对每个轨迹点对应的关节角进行修正，将修正后的关节角代入式（20）得到修正后的轨迹，效果如图4所示，轨迹上每隔80个采样点作一个标记。

仿真结果中，修正前轨迹的平均位置误差为14.21 mm，修正后轨迹的平均位置误差为0.002 mm。结果表明，本文所提算法能很好地通过修正关节角对连续的轨迹点进行修正，修正后的轨迹表现稳定且贴近期望轨迹。

4.2 实验验证

本节通过实验来验证算法的有效性，实验中直接使用实际采集到的末端位姿数据作为第1节误差补偿算法步骤（2）中的实际末端位姿，即该步骤变为每次将关节角θ（k）a输入机器人，测量得到实际末端位姿T（k）a。本次实验的操作对象为UR10机器人（重复定位精度为±0.03 mm），测量设备使用Leica AT901-MR激光跟踪仪系统（测量精度为±15 μm+6 μm/m），在机器人末端安装3个靶球用于位姿测量，实验现场如图5所示。

在机器人工作空间内随机选择若干位姿作为目标位姿Td，实验过程按照第1节补偿算法流程进行，并测量记录实际位姿误差。图6展示了某个目标位姿的误差补偿过程，姿态表示使用Z-Y-Z序列欧拉角，伪目标生成方式选用欧拉角法。

由图6可知，第一次补偿已经能够大幅度降低误差，多次补偿后位姿精度得到明显提高。位置误差从0.8756 mm降低到0.0359 mm，姿态误差从0.3930°减小到0.0084°（取三个分量平方和的开方）。下面选取多组不同目标位姿进行实验，每次实验进行2次补偿，伪目标生成法使用欧拉角法，记录补偿前后的误差，结果如图7所示。为了更好地观察补偿效果，图中补偿前误差均取绝对值。

经过统计，平均位置误差从1.1257 mm减小到0.0262 mm，最大位置误差减小到0.0577 mm。平均姿态误差从0.3155°减小到0.012°，最大姿态误差减小到0.0247°。实验结果表明本文提出的误差补償算法能够有效地补偿机器人末端位姿误差，并且补偿效率高。

5 结论

本文提出的误差补偿算法能够通过修正关节角来补偿辨识出的误差，误差补偿仿真和实验结果表明：

（1）算法误差补偿效果很好，实验中能使机器人的末端位置误差最大值保持在0.06 mm以内，并且算法耗时短、效率高。仿真结果表明算法能有效减小轨迹的平均位置误差，且修正后的轨迹表现稳定。

（2）本文算法可以用于任何形式的误差辨识后的误差补偿步骤，有较广的应用前景。不同的伪目标生成算法各有特点，可以根据实际应用场景和具体需求来进行选择。在只考虑位置误差的情况下，应该优先考虑使用计算量少的固定姿态法；在考虑位姿误差的情况下，可以优先使用单位四元数法和直接相乘法；在时间允许的情况下，可以选择集成多种算法进一步提高补偿效果。

（3）如果机器人在点位控制中可以实时测量反馈末端实际位姿并允许迭代补偿，那么可以将实际测量的位姿替换算法中通過函数预测的实际位姿，实现更精确的实时补偿功能。

参考文献：

［1］ 付鹏强， 姜晓灿， 苗宇航， 等. 工业机器人绝对定位误差补偿技术研究进展［J］. 科技导报， 2021， 39（13）：93-107.

FU Pengqiang， JIANG Xiaocan， MIAO Yuhang， et al. Summary of Absolute Positioning Error Compensation Technology for Industrial Robots［J］. Science and Technology Review， 2021， 39（13）：93-107.

［2］ 张文彬. 六自由度串联工业机器人定位误差分级补偿方法研究［D］. 武汉：华中科技大学， 2021.

ZHANG Wenbin. Research on Hierarchical Compensation Method for Positionning Error of 6-DOF Series Industrial Robot［D］. Wuhan：Huazhong University of Science and Technology， 2021.

［3］ ZENG Y， TIAN W， LIAO W. Positional Error Similarity Analysis for Error Compensation of Industrial Robots［J］. Robotics and Computer-integrated Manufacturing， 2016， 42：113-120.

［4］ CHEN D， YUAN P， WANG T， et al. A Compensation Method for Enhancing Aviation Drilling Robot Accuracy Based on Co-Kriging［J］. International Journal of Precision Engineering and Manufacturing， 2018， 19（8）：1133-1142.

［5］ ANGELIDIS A， VOSNIAKOS G C. Prediction and Compensation of Relative Position Error along Industrial Robot End-effector Paths［J］. International Journal of Precision Engineering and Manufacturing， 2014， 15（1）：63-73.

［6］ 倪华康， 杨泽源， 杨一帆， 等. 考虑基坐标系误差的机器人运动学标定方法［J］. 中国机械工程， 2022， 33（6）：647-655.

NI Huakang， YANG Zeyuan， YANG Yifan， et al. Robot Kinematics Calibration Method Considering Base Frame Errors［J］. China Mechanical Engineering， 2022， 33（6）：647-655.

［7］ 陈宵燕. 工业机器人多模式标定及刚柔耦合误差补偿方法研究［D］. 无锡：江南大学， 2020.

CHEN Xiaoyan. Research on Multi-mode Calibration and Rigid-flexible Coupling Error Compensation Method for Industrial Robot［D］. Wuxi：Jiangnan University， 2020.

［8］ 何庆稀， 游震洲， 孔向东. 一种基于位姿反馈的工业机器人定位补偿方法［J］. 中国机械工程， 2016， 27（7）：872-876.

HE Qingxi， YOU Zhenzhou， KONG Xiangdong. Positioning Error Compensation Method of Industrial Robot Based on Closed-loop Feedback of Position and Orientation［J］. China Mechanical Engineering， 2016， 27（7）：872-876.

［9］ 焦国太， 李庆， 冯永和， 等. 机器人位姿误差的综合补偿［J］. 华北工学院学报， 2003，24（2）：104-107.

JIAO Guotai， LI Qing， FENG Yonghe， et al. A Compensation Method of the Robot Pose Error［J］. Journal of North China Institute of Technology， 2003，24（2）：104-107.

［10］ NGUYEN H N， ZHOU J， KANG H J. A Calibration Method for Enhancing Robot Accuracy through Integration of an Extended Kalman Filter Algorithm and an Artificial Neural Network［J］. Neurocomputing， 2015， 151：996-1005.

［11］ 奚陶. 工业机器人运动学标定与误差补偿研究［D］. 武汉：华中科技大学， 2012.

XI Tao. Research on Kinematic Calibration and Error Compensation of Industrial Robot［D］. Wuhan：Huazhong University of Science and Technology， 2012.

［12］ DEVLIEG R， SZALLAY T. Improved Accuracy of Unguided Articulated Robots［J］. SAE International Journal of Aerospace， 2009， 2（1）：40-45.

［13］ 尹仕斌. 工業机器人定位误差分级补偿与精度维护方法研究［D］. 天津：天津大学， 2015.

YIN Shibin. Research on the Graded Calibration and Accuracy Maintenance Technique for Industrial Robot［D］. Tianjin：Tianjin University， 2015.

［14］ 温秀兰， 崔俊宇， 芮平， 等. 轴线测量与迭代补偿的机器人几何参数标定［J］. 计量学报， 2018， 39（4）：449-454.

WEN Xiulan， CUI Junyu， RUI Ping， et al. Robot Geometric Parameters Calibration Based on Axis Measurement and Iterative Compensation［J］. Acta Metrologica Sinica， 2018， 39（4）：449-454.

［15］ SUGIHARA T. Solvability-unconcerned Inverse Kinematics by the Levenberg-Marquardt Method［J］. IEEE Transactions on Robotics， 2011， 27（5）：984-991.

［16］ 董贵荣， 张富强， 侯丕鸿， 等. 基于四元数的工业机器人逆运动学避障求解［J］. 数字印刷， 2022（3）：49-56.

DONG Guirong， ZHANG Fuqiang， HOU Pihong， et al. Inverse Kinematics Obstacle Avoidance Solution for Industrial Robot Based on Quaternion［J］. Digital Printing， 2022（3）：49-56.

［17］ 谢文雅. 基于四元数的工业机器人姿态规划与插补算法的研究［D］. 武汉：华中科技大学， 2017.

XIE Wenya. Research of the Orientation Planing and Interpolation for Industrial Robots Based on Quaternion［D］. Wuhan：Huazhong University of Science and Technology， 2017.