考虑齿形误差影响的摆线针轮承载特性分析

李天兴,夏鑫博,吴 丹,姚 建,代 震,张 阳

(1.河南科技大学 机电工程学院,河南 洛阳 471003; 2.慈溪技师学院 机械工程系,浙江 宁波 315327)

0 引言

旋转矢量(rotate vector,RV)减速器是工业机器人最核心的零部件[1-2],而摆线针轮副的承载特性决定了RV减速器的承载能力和传动精度[3-4]。受加工设备和生产工艺的限制,摆线轮的齿形误差无法根除,因此探究摆线轮齿形误差对摆线针轮副承载特性的影响十分重要。

许多学者在摆线轮齿形误差及其承载啮合特性方面进行了研究。文献[5]利用消隙法分析了摆线针轮副的承载特性,解决了传统方法难以判别啮合区间的不确定性问题。文献[6-7]综合考虑了摆线轮的齿廓误差,提出了RV摆线针轮副真实啮合侧隙和啮合点的确定方法,解决了真实啮合位置和理论啮合点不一致的难题。文献[8]依据啮合原理对摆线轮真实齿面进行了啮合分析,获得了考虑齿廓误差的摆线针轮副真实传动误差。文献[9]同时考虑了摆线针轮的侧隙和齿廓误差,发现齿廓误差会导致摆线针轮副的真实啮合齿数减少,摆线针轮负载集中。文献[10]考虑了摆线轮齿廓误差,利用有限元构建了摆线轮真实齿廓误差模型,分析了齿形误差和啮合接触力之间的关系。文献[11-12]考虑了摆线轮齿廓误差,分析了摆线针轮副的啮合特性,空载传动误差较理论状态增加了近百倍。文献[13-14]结合摆线轮的齿廓误差与修形量,构建了真实状态下的摆线针轮啮合模型,探究了齿形误差与啮合应力和传动误差的关系。文献[15]考虑了摆线轮磨损状态下的齿廓误差,提出了摆线针轮真实传动误差与扭转刚度的计算方法。综上所述,摆线针轮副的负载啮合特性分析大多是在不考虑齿形误差的理想情况下进行的,与工程应用中的实际状况差异较大,而关于齿形误差影响下的实际承载特性的研究相对不足。

鉴于此,本文综合考虑了摆线轮的齿形误差,提出了1种能够反映实际啮合状态的摆线针轮副承载特性分析方法,探究了摆线轮齿形误差对其承载特性的影响,期望为RV减速器承载性能的提升和预控提供有效的保证。

1 摆线针轮副误差齿廓接触分析

1.1 摆线轮误差齿廓

为确定摆线轮的齿廓误差,本文以摆线轮齿根点为测量起点,根据离散点接触跟踪测量方法对摆线轮进行单齿廓测量。摆线轮误差齿廓模型如图1所示,以设计齿廓R上P0点为例,过其法矢n,确定与P0对应的实际齿廓R*上的点P*,两点间的偏差为齿廓误差δ′:

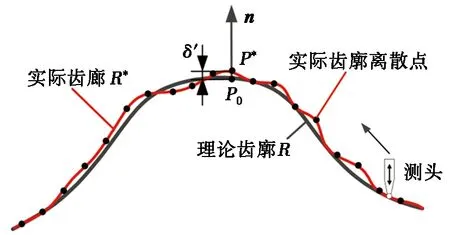
图1 误差齿廓模型

δ′=(R*-R)n。

(1)

(2)

其中:(xc(αi),yc(αi))为摆线轮设计齿廓坐标,nxc(αi),nyc(αi)为单位法矢量在x、y上的分量。

由式(2)得到的摆线轮齿面离散点无法表征摆线轮的连续齿廓,因此需要对离散点进行拟合。三次非均匀B样条曲线对摆线轮真实齿廓具有较高的拟合精度,故本文选用该方法重构摆线轮实际齿廓。摆线轮的齿宽为常数,故可忽略其齿宽误差,将其简化为二维模型,此时摆线轮误差齿廓方程为:

(3)

其中:n为控制顶点数;Ni,3(u)为三次B样条基函数;Pi为控制顶点矢量;参变量u的取值为0≤u≤1。

1.2 摆线针轮齿面接触分析

为直观表述摆线针轮的啮合形态,在保证其啮合特性不变的情况下,通过坐标转换原理建立了摆线针轮啮合坐标系,如图2所示:(xf,yf)为定坐标系,Of为坐标原点;动坐标系(xp,yp)和(xc,yc)分别与针轮和摆线轮固连,Op、Oc为对应坐标系原点;原点Of与Op重合,φ1和φ2分别为针轮和摆线轮的转角;Op和Oc之间的距离为偏心距a;β是针齿参量角。

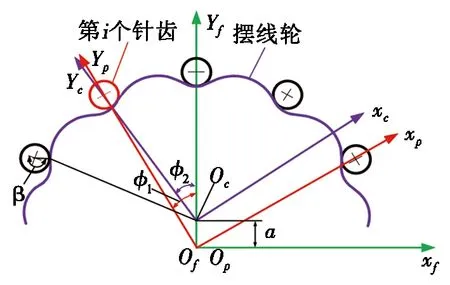
图2 摆线针轮副啮合坐标系

根据轮齿啮合原理可知,摆线轮和针轮在啮合位置处的位置矢量和单位法矢分别相等,则E-TCA方程组可表示为:

(4)

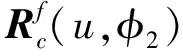
方程组(4)中有3个非线性方程,4个未知量,无法求解。假定主动轮转角φ1初始值为φ10,以Δφ为增量,以初始啮合点为起始点,利用牛顿迭代法求解E-TCA方程,可得到一系列对应的啮合参数,直至针齿脱离啮合。

分析摆线针轮接触模型要先明确初始啮合点位置,齿形误差导致使用节点确定摆线针轮初始啮合点位置的常规方法不再适用,本文利用针轮转角来确定其初始啮合点。将摆线轮保持固定不动,依次滚动所有针齿,直至接触摆线轮,对比各针齿转角,其中转角最小的针齿与摆线轮的啮合点即初始啮合点位置。

由于摆线轮存在齿形误差,传统的啮合间隙计算公式无法真实表达其啮合间隙,文献[16]给出了包含摆线轮齿形误差的啮合间隙di(i为针齿号):

(5)

其中:(xpi,ypi)为针齿中心坐标;(xci,yci)为摆线轮距针齿中心最近的齿廓坐标;rrp为针轮曲率半径。

2 考虑齿形误差的承载模型及分析策略

空载时,摆线针轮副仅有1对齿啮合,其他轮齿均存在不同的侧隙。当施加载荷后,摆线针轮会出现弹性变形,初始啮合位置的弹性变形最大。将E-TCA模型得到的啮合间隙和最大弹性变形量进行对比,以此判断摆线针轮的可能啮合齿数与区间,结合能量最低原理确定其真实承载特性。

2.1 考虑齿形误差的承载分析模型

尽管摆线轮存在齿形误差,但在承载特性分析时仍满足Hertz接触理论、变形协调关系和力矩平衡原理。基于此,构建包含齿廓误差的摆线针轮承载分析模型。

摆线针轮副的接触印痕在空载时是1条线段,但随着施加载荷的增大会逐渐变形为矩形。摆线针轮接触模型如图3所示。

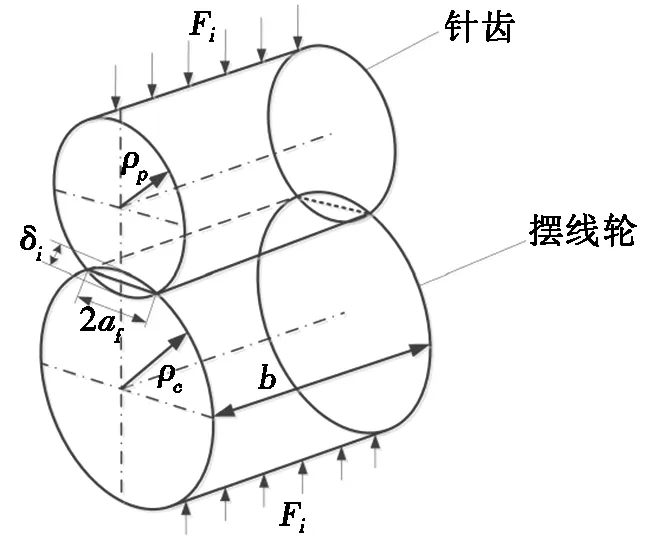
图3 摆线针轮接触模型

根据Hertz接触理论[17],摆线针轮的接触半宽ai与弹性变形量δi可表示为:

(6)

(7)

其中:ρi为摆线针轮综合曲率半径;Fi为接触力;b为摆线轮齿宽;μ1和μ2分别为摆线轮与针轮的泊松比;E1和E2分别为摆线轮与针轮的弹性模量;δci和δpi分别为摆线轮与针轮的弹性变形量;ρci为摆线轮接触点的曲率半径;rrp是针轮曲率半径。

摆线针轮副完成多齿同时啮合的条件是啮合点处的误差转角si满足变形协调关系。转角误差si是由接触力臂Li、变形量δi和啮合间隙di共同导致,且处处相等,变形协调关系可表示为:

(8)

由力矩平衡原理可知:当摆线传动系统达到平衡状况时,摆线轮所承载的全部力矩T之和为零。在不考虑力的正负号时,力矩平衡方程可表示为:

(9)

其中:n为啮合齿数;Fi为接触力;Li为接触力臂。

江西省水资源的一个不利特点，是时空分布不均、水资源分布与需求不匹配。全年降雨量的60%左右集中在主汛期4—6月，而用水量的60%则集中在主汛期后的7—9月，由于控制性水利工程少，往往出现汛期洪水成灾、汛后无水可用的局面。水资源开发利用能力不足，特别是水资源调蓄能力不足、供水保证率不高、水资源开发利用率偏低等问题仍然比较突出。一些水问题逐渐显现，甚至成为经济社会发展的制约因素。

2.2 能量最低原理及承载分析策略

由于摆线轮齿形误差的存在,导致摆线针轮副的真实啮合齿数及区间难以确定,但其满足能量最低原理。依据能量最低原理可知,当系统处于平稳状况时的总能量最低[18-19]。摆线针轮副的系统总能量NE是n个啮合齿对的啮合接触力Fi与弹性变形量δi的乘积之和:

(10)

根据考虑摆线轮齿形误差时的初始啮合参数确定方法和承载接触分析模型,结合能量最低原理,其承载特性分析流程如图4所示。

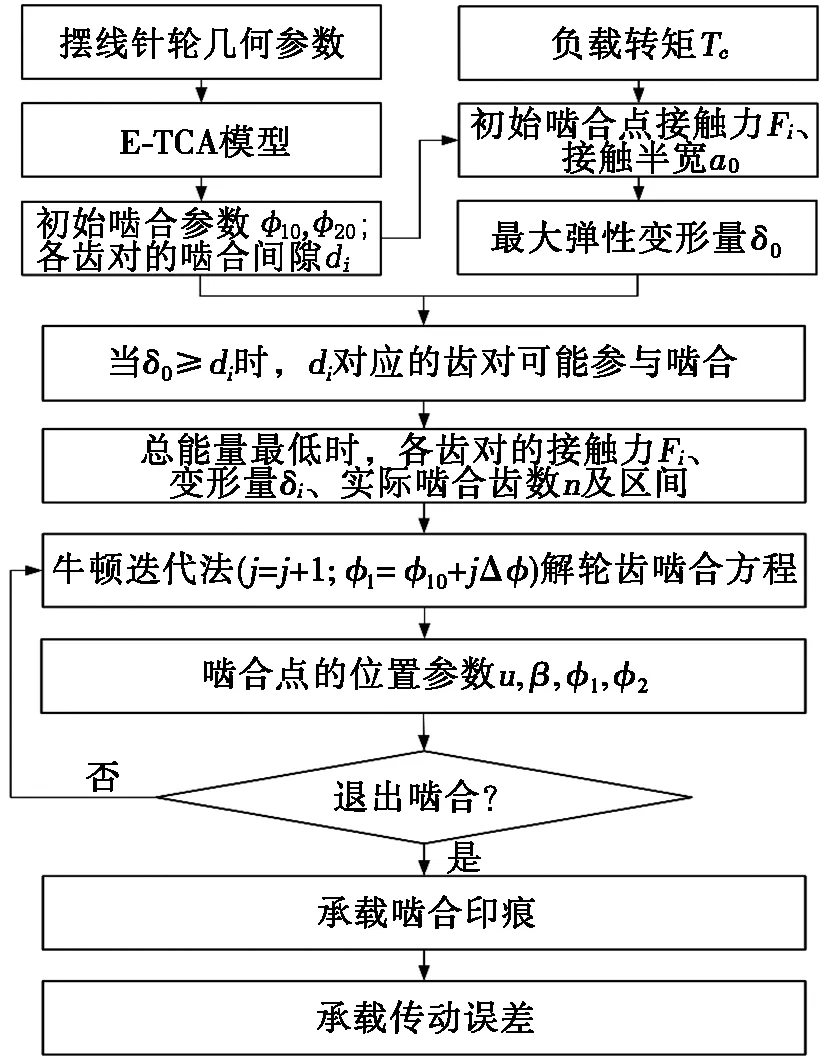
图4 摆线针轮副承载分析流程

(Ⅰ)利用E-TCA模型确定其初始啮合点位置参数及各啮合点间隙。

(Ⅱ)负载后,根据初始啮合点处的接触力和接触半宽的非线性关系计算出最大弹性变形量。

(Ⅲ)对比各齿对啮合间隙和初始啮合点的最大弹性变形量,判断可能的啮合齿数及区间。

(Ⅳ)根据承载啮合模型,分别计算不同啮合齿数时各啮合点处的接触力和弹性变形量。

(Ⅴ)分析各可能啮合状况下的系统总能量,能量最低时的啮合齿数与区间即真实啮合状态。

(Ⅵ)给定针轮初始转角,利用牛顿迭代法计算E-TCA方程组,获取各啮合点的位置参数,直至脱离啮合。

(Ⅶ)根据摆线针轮啮合参数,确定承载下的接触印痕;利用摆线针轮副的真实输出转角和理论输出转角之差确定承载传动误差。

3 齿形误差对承载特性的影响分析与验证

本文以RV-40E型减速器中的摆线针轮为例,其基本参数如表1所示。如图5所示,利用JD45+测量机在摆线轮齿廓上测量了1 200个点,获取了如图6所示的摆线轮齿形误差,齿形误差中存在1个突异点0.021 mm,为避免该突异点影响摆线轮齿廓重构,对齿形误差进行了均值滤波处理,此时摆线轮齿形误差幅度为-0.013～0.011 mm。

表1 摆线针轮基本参数

图5 摆线轮齿形误差测量

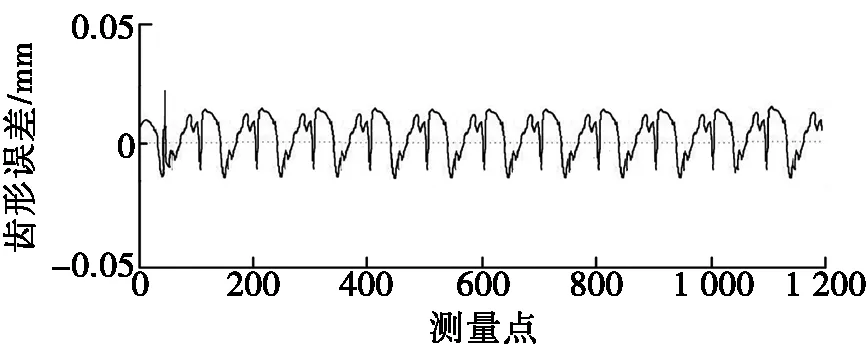
图6 摆线轮齿形误差

利用三次非均匀B样条曲线对摆线轮实际齿廓进行重构,最大重构偏差为8.6×10-10mm,满足精度要求,因此可用拟合得到的数字化齿廓探究摆线轮齿形误差对承载特性的影响。同样以RV-40E型减速器中的摆线针轮副为例,对其施加T=50 N·m的转矩进行承载特性分析。

同时为了验证承载特性分析方法的正确性与可行性,进行了有限元分析。根据表1中的摆线针轮基本参数,结合摆线轮误差数据,在UG软件中构建了包含齿形误差的摆线针轮三维模型,将其导入ABAQUS有限元分析软件中。采用Free对摆线轮和针轮进行网格划分,并在接触面上进行网格加密,网格数分别为216 973和186 769个。将摆线针轮副定义为摩擦因数为0.05的面面接触。在摆线轮上施加T=50 N·m顺时针负载转矩,在针轮上施加0.02 rad/s的逆时针转速,施加完全约束来模拟摆线轮的偏心运动。

3.1 承载啮合区间

根据式(5)计算出摆线针轮副的啮合间隙分布趋势,如图7所示。由图7可知:2种情况下的第5号齿对处的啮合间隙均为0,即二者的初始啮合点均发生在第5对齿。2种情况下的啮合间隙对比承载后,根据式(7)计算出2种情况下的初始啮合点处的最大变形量,如图7所示,红色和黑色横线分别表示考虑齿形误差与不考虑齿形误差的最大变形量。当齿侧间隙小于等于最大变形量时,对应齿对可能参与啮合,则2种情况下的可能啮合齿数为1～21。利用能量最低原理分析得出考虑齿形误差和不考虑齿形误差的系统最低总能量分别为289.5 J、307.6 J,二者对应的啮合区间分别为1～15齿和1～16齿,啮合齿数减少了1对。

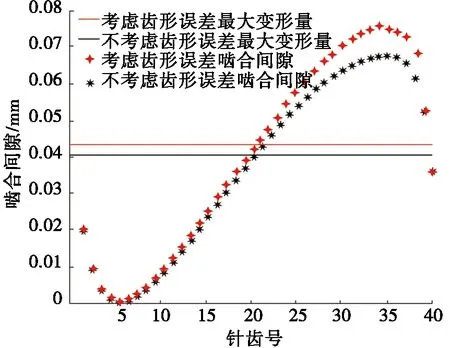
图7 两种情况下的啮合间隙对比

有限元分析完成后,在可视化功能模块查看摆线轮啮合印痕,如图8所示。蓝色线段代表啮合痕迹,啮合区间为1～15齿,齿数为15,第5号针齿的啮合印痕最宽,代表初始啮合点发生在第5号针齿处,初始啮合点、啮合齿数和啮合区间与理论结果完全一致。

图8 摆线轮啮合印痕

3.2 承载啮合印痕

利用摆线针轮副的承载接触模型,分别计算出2种情况的啮合点位置αi与接触半宽αi,如表2所示。为便于观察,将其承载接触印痕集中于同一齿面上,2种情况下的承载啮合印痕如图9所示。由图9可知:二者啮合印痕的最宽处与最大差值均在第5号齿对,不考虑齿形误差时,啮合印痕由0.144 mm增至0.492 mm,再逐渐减小至0.252 mm;考虑齿形误差时,啮合印痕由0.139 mm增至0.518 mm,随后减至0.247 mm。啮合印痕峰值增大了0.026 mm,最大差值为5.2%,第4齿到第10齿的啮合印痕宽度增大,其余齿的啮合印痕宽度变小,导致受力更加集中。

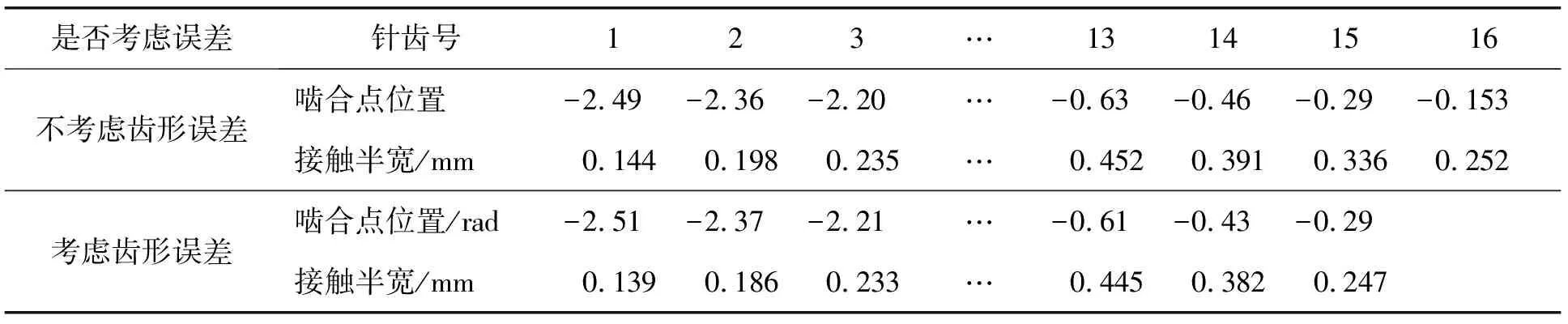
表2 啮合点位置及接触半宽

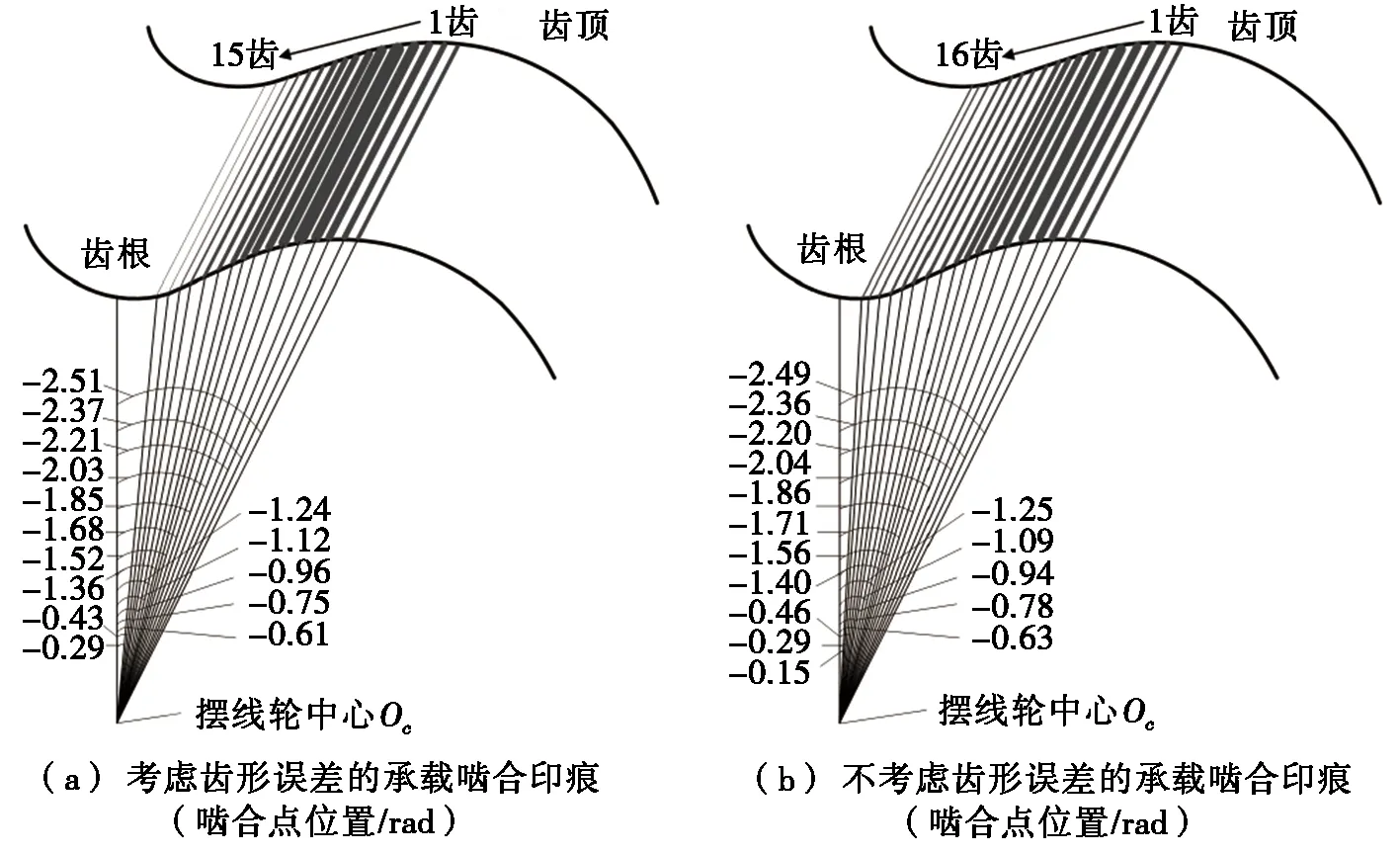
图9 摆线轮负载啮合印痕

3.3 承载啮合应力

根据赫兹接触理论可知接触应力σi的公式为[20]:

(11)

根据式(11)得到了2种情况下的啮合应力,如图10所示。由图10可知:二者变化趋势均为随针齿号增大先增至峰值,随后逐渐减小。不考虑齿形误差时,最大应力值494.37 MPa出现在第8号齿对处;存在齿形误差时,最大啮合应力值520.68 MPa出现在第9号齿对处,峰值应力相差5.3%。这是因为摆线轮齿形误差导致啮合点处的接触力和综合曲率半径均发生了变化。

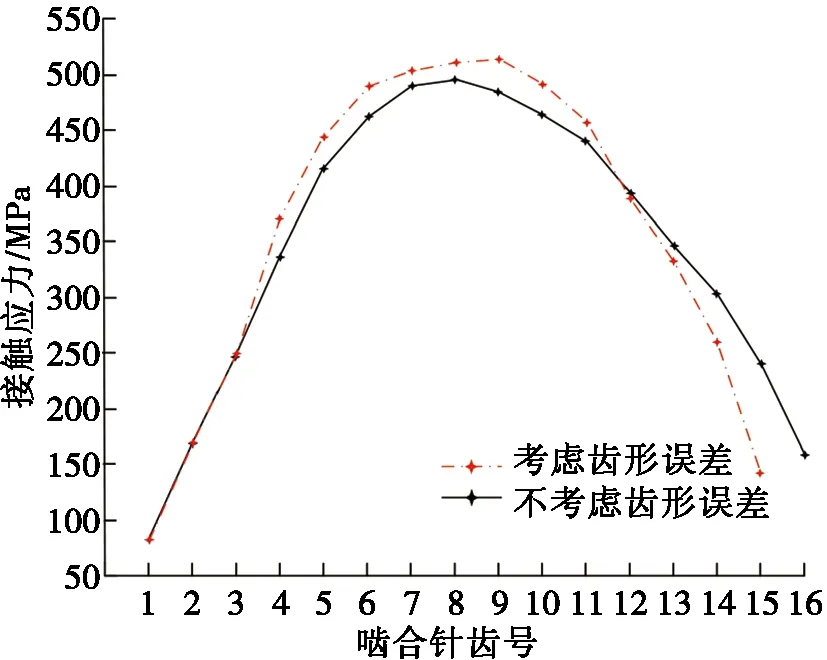
图10 啮合点处的接触应力

在有限元可视化模块中导出摆线轮的啮合应力,如图11所示。由图11可知:最大啮合应力为509 MPa,与理论结果相差2.2%,均小于GCr15轴承钢许用应力,满足其强度要求,且变化趋势相同。

图11 摆线轮的啮合应力云图

3.4 承载传动误差

传动误差Δφe是指传动装置的实际输出转角与理论输出转角的差值[21]:

Δφe=Δφi/i-Δφo,

(12)

其中:i为传动比;Δφi为输入转角;Δφo为输出转角。

不断改变针轮输入转角,求解得到对应摆线轮输出转角,结合式(12)得到了2种情况下的加载传动误差,如图12所示。由图12可知:二者呈周期性变化且趋势一致。不考虑齿形误差时,随针轮转角增加,传动误差先逐渐减至最小值-6.489′,再缓慢增至峰值-6.559′,随后进入到下个周期,传动误差曲线的波动幅度为0.07′。考虑齿形误差时,随着针轮转角的逐渐增加,承载传动误差先不断减小至最小值-6.617′,随后增至最大值-6.691′,承载传动误差波动幅值为0.074′,但在进入下个周期时有明显跳动。考虑齿形误差时的波动幅度增大了5.7%,使得传动精度和平稳性恶化。

图12 承载传动误差曲线

将有限元分析得到的摆线针轮副的输入转角和输出转角代入式(12),得到了摆线针轮副在旋转1周内的传动误差,如图13所示。与图12中的包含齿形误差的传动误差曲线对比,二者均呈周期性变化,在同一周期内均是先逐渐减小至最小值,再逐渐增大,趋势基本一致,有限元分析的承载传动误差幅值为0.071′,略小于理论结果。这是因为有限元结果受网格划分精度、边界约束、接触对设置等因素的影响,但二者的误差仅为4%,满足精度要求。因此仿真分析验证了理论模型的可行性。

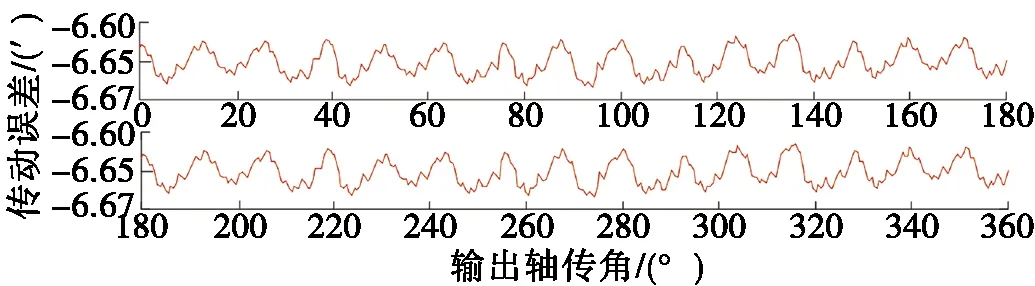
图13 有限元承载传动误差

4 结论

(1)本文综合考虑了摆线轮的齿形误差,采用三次非均匀B样条拟合出摆线轮真实齿廓,基于此,建立了E-TCA分析模型,得知齿形误差的存在导致实际啮合间隙增大。

(2)建立了包含齿形误差的承载接触分析模型,利用能量最低原理确定了实际承载啮合区间和负载状况。

(3)利用有限元模型验证了理论模型的正确性。由于齿形误差的影响,同时啮合齿数减少了1对,啮合应力和传动误差增大了5.3%和5.7%。