基于MPC的智能车辆路径规划与跟踪控制

张丽霞,田 硕,潘福全,严涛峰,李宝刚

(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)

0 引言

智能车辆是聚集了先进感知系统、规划决策系统、跟踪控制系统、执行系统、多辅助驾驶系统的1个综合体[1]。目前,对路径规划与跟踪控制已经进行了很多研究,但是在面对复杂工况和曲率较大的路况时,跟踪控制的效果仍然不理想。

研究路径规划算法,实现智能汽车在不同环境下的精准避障,可为车辆提供一条安全、可靠的避障路径[2-3]。文献[4]在结合智能汽车动力学约束条件的基础上,提出一种基于蚁群算法优化的最佳路径设计,经过仿真验证,该算法可以提高全局搜索能力,减少节点数量,有效地降低汽车行驶能耗。文献[5]提出一种基于模糊控制的避障路径规划器,通过超声波测距传感器测出左、右、前三方的距离,将其作为模糊控制的输入,以车辆转向角作为输出,建立模糊控制规则。文献[6]在人工势场基础上建立目标点引力函数,并引入障碍物约束和车辆动力学约束,建立改进的人工势场模型。文献[7]在人工势场模型中引入道路边界斥力势场来进行转向避障路径的规划,并用椭圆形势场代替了原来的斥力势场。通过仿真试验,证明了采用该方法可获得安全的局部避障路径。文献[3]针对传统人工势场(artificial potential field,APF)算法易陷入局部极值的问题,引入Bug算法。通过搭建智能车实验平台证明了改进的APF-Bug混合算法可以有效提高智能车在行驶过程中的安全性。

路径跟踪控制主要通过控制车辆的前轮转角和油门/刹车踏板,使车辆的行驶路径与规划路径间的横向偏差与横摆角偏差尽可能小[8]。文献[9]以期望航向和实际航向的偏差作为反馈,通过设计鲁棒比例积分微分(proportional-integral-derivative,PID)控制器计算控制量。经过验证,所提出的路径跟踪横向控制策略跟踪效果较好。文献[10]建立14自由度车辆模型,提出了一种以8自由度车辆模型作为预测模型的模型预测控制(model predictive control,MPC)方法。从MPC控制器中生成最优车轮转向角序列,并以曲率连续变化的曲线作为参考轨迹。文献[11]建立了线性时变路径跟踪预测模型,并在目标函数中引入向量松弛因子,将路径跟踪问题转化为带软约束的二次规划问题。文献[12]提出一种基于滑膜变结构的控制方法,分别引入积分滑膜项和模糊自适应项,用于车辆转向时的车速和转向角速度的控制。

综合国内外研究发现,针对避障路径规划,多数使用单个规划算法,得到的规划效果不是很理想,如:蚁群算法的搜索效率不高,易受到局部最优解的影响[13];模糊控制在复杂的环境下,规则库难以建立[14];人工势场法具有效率高、适应性好等优点,但也存在局部最优等缺陷[15]。针对路径跟踪控制,PID控制虽然易于实现,但其抗干扰能力和鲁棒性不强,存在对扰动敏感、误差计算不合理等问题[16]。MPC控制方法虽然能够补偿模型误差,控制较为精确,但MPC的权重系数为固定值,无法满足某些工况对其精度和稳定性的要求[17]。综上,本文采用基于MPC和改进的APF算法,既解决了传统APF的缺陷,又在考虑车辆动力学特性下,有效地进行动态避障路径规划。同时根据车辆横向偏差和参考路径曲率,引入模糊控制对MPC横向路径跟踪控制器权重系数进行优化,提高了跟踪精度及稳定性。

1 车辆动力学模型

建立三自由度车辆动力学模型,如图1所示。图1中,坐标系X-O-Y为大地坐标系,坐标系x-o-y为车辆坐标系,x轴沿车辆纵轴向前为正,y轴垂直于车辆纵轴指向驾驶员左侧为正。

根据图1可得车辆动力学方程:

(1)

其中:m为整车质量,kg;vx为车辆纵向速度,m/s;vy为车辆横向速度,m/s;φ为车辆横摆角速度,rad/s;Fxf、Fxr为车辆坐标系下x轴方向前、后轮胎受到的力,N;Flf、Flr为前、后轮胎受到的纵向力,N;δ为前轮转角,rad;Fyf、Fyr为车辆坐标系下y轴方向前、后轮胎受到的力,N;Fcf、Fcr为前、后轮胎受到的侧向力,N;Iz为车辆绕z轴的转动惯量,kg·m2;a为前轴到质心处的距离,m;b为后轴到质心处的距离,m。

轮胎的纵向力和侧向力可用线性函数近似表示为:

(2)

其中:cli为轮胎纵向刚度,N/m;cci为轮胎侧偏刚度,N/rad;si为轮胎滑移率;αi为轮胎侧偏角,rad。

通过对以上各式进行简化和推导,可得到基于小角度和线性轮胎模型假设条件下的车辆非线性系统动力学模型:

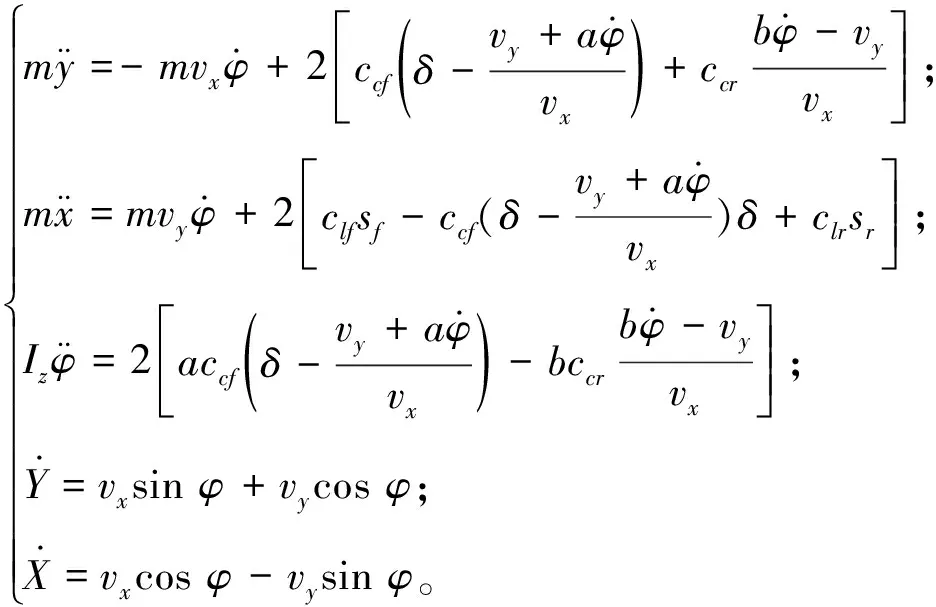
(3)

2 基于MPC和改进APF的避障路径动态规划器设计

针对传统APF中存在的目标不可达、局部最优等缺陷,本文改进障碍物斥力势场,添加道路边界约束、速度斥力约束、车道引力约束等多个约束条件,建立改进APF;同时考虑到车辆动力学特性,结合MPC,设计了基于MPC和改进APF的避障路径动态规划器。

在路径规划过程中,将车辆简化为质点。车辆行驶环境状况中的目标点位置、障碍物位置和车辆自身位置均由感知层确定。车辆的位置为q(x,y)T,障碍物的位置为qob(xob,yob)T,目标点的位置为qg(xg,yg)T。

引力势场函数可表示为:

(4)

其中:κ为引力势场尺度因子;d(qg,q)为车辆与目标点间的欧几里德距离,方向为车辆指向目标点,m。

在路径规划过程中,不仅考虑躲避障碍物,还要考虑车辆驶出道路边界影响安全的因素。故建立道路边界斥力势场为:

(5)

其中:ηedge1、ηedge2为道路边界斥力势场增益系数;yl、yr分别为左右车道中心线的横向位置,m;L为道路宽度,m。

在传统人工势场法中,障碍物处于其对车辆产生作用的最大距离区域d0内时,行驶车辆才受到斥力作用,但障碍物形状多样,固定的参数无法满足实际行驶的场景,所以改进为椭圆形斥力势场。因此本文建立改进的障碍物斥力势场函数为:

(6)

在车辆的整个行驶环境中,不仅有静态障碍物,还存在动态障碍物,在建立障碍物斥力势场时,不仅要考虑被控车辆距障碍物的距离,还应考虑障碍物速度影响。图2为被控车辆与障碍物的速度方向示意图。

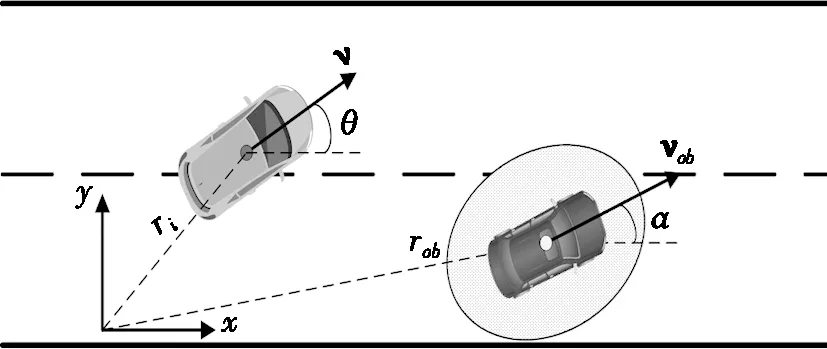
图2 速度方向示意图

速度斥力势场函数可表达为:

(7)

其中:ηvel为速度斥力势场尺度因子。

车辆在行驶和转向避障时,主要沿着车道中心线行驶。本文以车道中心线为引力点建立车道引力势场模型,以前方车道中心线上各点为引力点,构建车道引力势场函数,其表达式为:

Ulane=kroad(|y-y0|2+|x-xd|),

(8)

其中:kroad为车道引力势场增益系数;y0为车辆起始横向位置坐标,m;xd为车辆转向区域的最大纵向距离,m。

综合上述分析,车辆在合力势场作用下的势能为:

Uall=Urep+Uroad+Uvel+Ulane+Uatt。

(9)

将改进APF建立的势场模型函数引入到MPC的目标函数和约束中,建立基于MPC和改进APF的避障路径动态规划器。

首先将式(3)转换为状态空间方程:

(10)

设计的目标函数如下:

(11)

其中:λφ为输出量权重矩阵;λU为环境势场权重矩阵;λu为控制增量权重矩阵。

各约束条件的取值参考文献[18]。基于MPC和改进APF的路径规划问题可转化为以下带约束问题:

(12)

通过对式(16)进行求解,可得到当前时刻的控制增量,进而确定当前时刻的控制量,如此循环迭代,得到预测时域内的最优路径点序列。

3 基于模糊MPC的车辆横向路径跟踪控制器设计

3.1 MPC控制器设计

根据文献[19],建立如下目标函数:

(13)

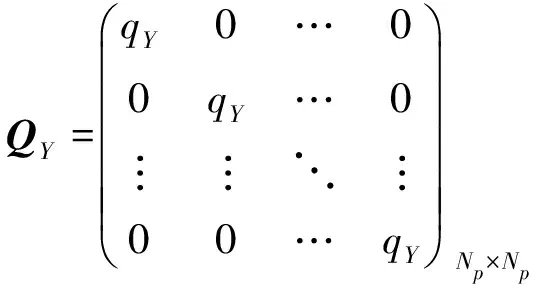
结合目标函数与约束条件,路径跟踪控制问题转化为求解如下带约束的二次规划问题:

(14)

最后通过对路径跟踪控制器的目标函数取最小,在每个控制周期内,可得到控制时域内一系列的控制增量序列,并将这一序列的第1个元素作为实际的控制输入增量作用到系统上。如此循环迭代,实现车辆对期望轨迹的跟踪。

3.2 模糊控制器设计

将横向偏差和参考路径曲率作为模糊控制的输入量,权重系数qφ和Ru的修正量Δqφ和ΔRu作为模糊控制的输出量,建立模糊规则。同时对于输入量选择三角形隶属度函数,输出量选择高斯隶属度函数,进而对MPC横向路径跟踪控制器的权重系数进行优化。

首先,需对模糊控制输入量进行归一化处理,有:

(15)

(16)

其中:eY,max、eY,min为最大、最小横向路径偏差,m;kmax、kmin为最大、最小参考路径曲率。

定义权重系数的调整算式为:

qφ=qφ0×100Δqφ;

(17)

Ru=Ru0×10ΔRu,

(18)

其中:qφ、Ru为模糊MPC控制器当前阶段计算出的权重系数;qφ0、Ru0为MPC控制器的权重系数,Δqφ、ΔRu为权重系数当前阶段的修正量。

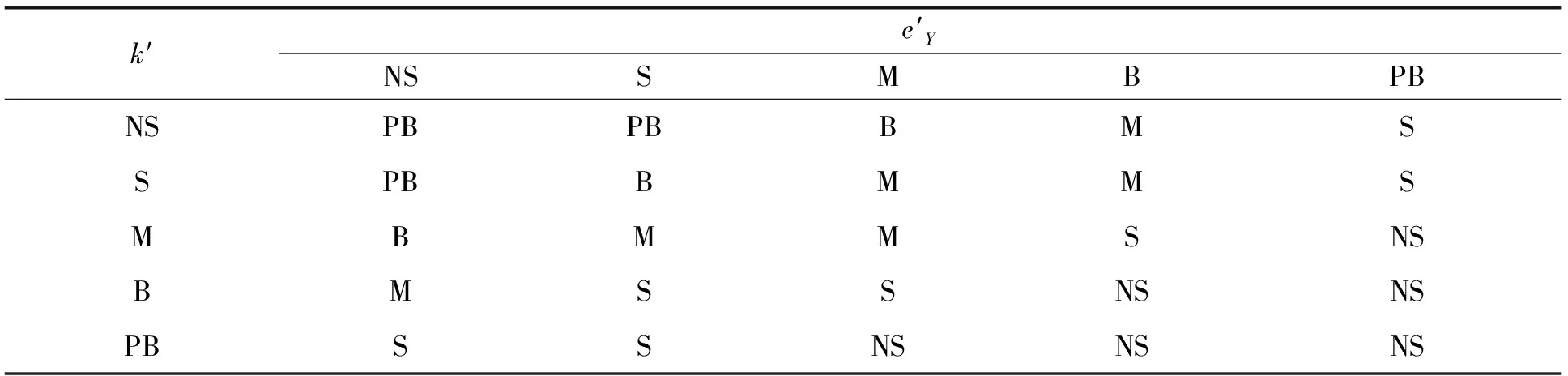
表1 Δqφ模糊控制规则表

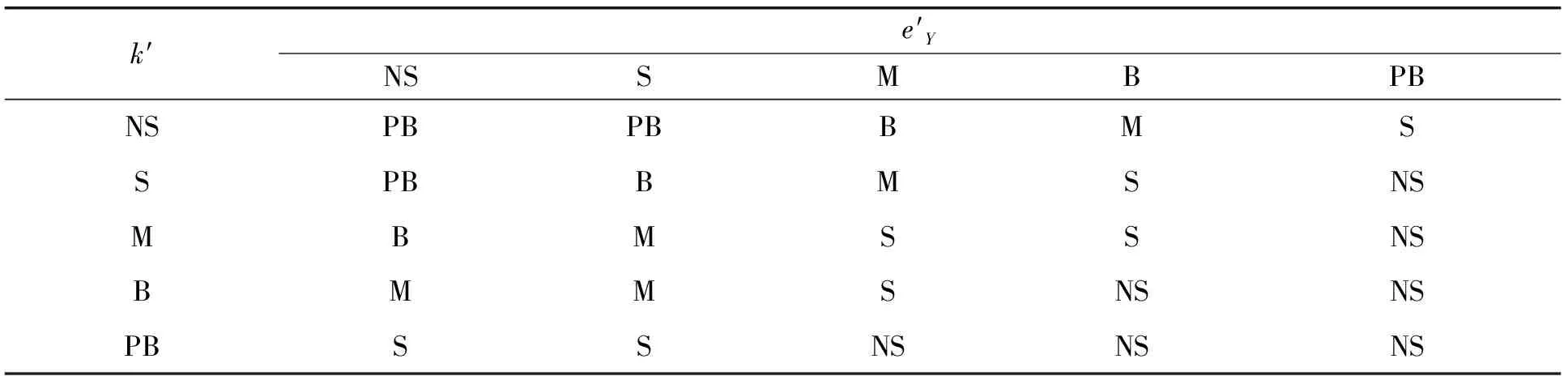
表2 ΔRu模糊控制规则表

经过模糊推理得出的结果不能直接作用于被控车辆,需经过反模糊化输出精确值,从而对权重系数进行调节。考虑到控制稳定性、抗干扰性和灵敏性的要求,本文采用面积重心法进行解模糊处理[20]。

为验证模糊MPC路径跟踪控制器的控制性能,选择权重系数为常量的MPC路径跟踪控制器和模糊MPC路径跟踪控制器进行仿真对比。选择双移线工况作为参考路径,车速设定为60 km/h。不同附着系数的路面会提供轮胎不同的侧向力,直接影响车辆的控制性能,因此本文分别选择μ=0.85 的干燥路面和μ=0.40的湿滑路面2种不同工况进行仿真实验,MPC路径跟踪控制器参数设置如表3所示。

表3 MPC路径跟踪控制器参数

测试工况一:车速60 km/h,路面附着系数0.85。

图3为路面附着系数0.85,60 km/h车速下2种控制器的跟踪结果对比。由图3a可以看出:2种控制器控制的车辆都能够较为精确地跟踪参考路径,但车辆在曲率较大的路段时,MPC路径跟踪控制器的最大横向偏差约为0.350 m,而模糊MPC路径跟踪控制器的最大横向偏差约为0.283 m,最大横向偏差减少19.14%,这是由于曲率较大的路段难以跟踪,模糊MPC路径跟踪控制器中的权重系数qφ和Ru变小,减小在该路段的横向偏差,使得车辆能够跟踪参考路径。由图3b可知:在 40 m的纵向范围内MPC控制器的横摆角轨迹跟踪最大偏差为 0.031 rad,模糊MPC控制器的最大偏差为 0.009 rad,因此模糊MPC控制器的轨迹跟踪更准确。从图3c和图3d可以看出:模糊MPC路径跟踪控制器的最大横摆角速度和前轮转角虽然比MPC路径跟踪控制器的最大值略有增加,稳定性有所降低,但保证了车辆的行驶安全性;同时整个轨迹跟踪过程中变化平缓,而且都处于约束范围内,说明此时车辆的稳定性良好。

(a) 车辆行驶路径

测试工况二:车速60 km/h,路面附着系数0.40。

图4为路面附着系数0.40,60 km/h车速下两种控制器的跟踪结果对比。由图4a和图4b可以看出:由于轮胎与地面摩擦力的下降,MPC路径跟踪控制器和模糊MPC路径跟踪控制器的轨迹跟随都存在一定的滞后性,在50 m的纵向范围内MPC控制器的横向偏差为0.651 m,模糊MPC控制器的横向偏差为0.1 m,相比较减少了0.551 m。同时在40 m范围内MPC控制器的横摆角轨迹跟踪最大偏差为 0.021 rad,模糊MPC控制器的最大偏差为 0.005 rad,由此模糊MPC控制器轨迹跟踪精度更高。从图4c与图4d可以看出:模糊MPC路径跟踪控制器的横摆角速度与前轮转角变化范围都因地面附着系数的减小而变大,但是没有发生突变,曲线变化始终平顺光滑,从始至终一直处于约束范围之内,车辆行驶稳定性良好。

(a) 车辆行驶路径

4 避障路径动态规划与跟踪控制试验验证

将设计的路径规划器和路径跟踪控制器进行联合,搭建避障路径规划与跟踪控制联合仿真模型,并进行动态障碍物不同速度下的避障路径规划与跟踪试验。

搭建的避障路径规划与跟踪控制联合仿真模型如图5所示。

图5 避障路径规划及跟踪控制联合仿真模型

基于MPC和改进APF的避障路径动态规划器参数如表4所示。

表4 基于MPC和改进APF的避障路径动态规划器参数

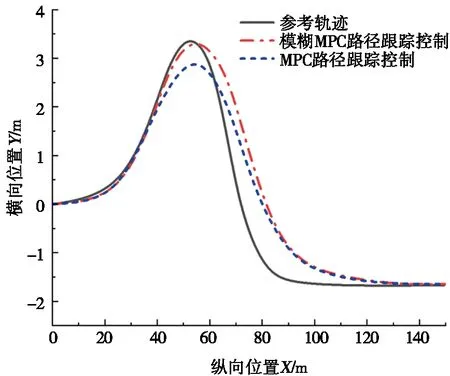
第1种工况距智能车辆约90 m处设有10 km/h的动态障碍物;第2种速度工况距智能车辆约130 m处设有20 km/h的动态障碍物;第3种工况距智能车辆约200 m处设有40 km/h的动态障碍物,沿着车道中心线行驶。动态障碍物不同速度下的避障路径规划及跟踪行驶曲线见图6,车辆行驶路径与规划路径的横向偏差见图7。智能车辆先沿着车道中心线行驶,检测到动态障碍物后,路径规划器规划出向左换道的路径,控制智能车辆开始向左侧换道避障,此时3种速度工况下的动态障碍物位置分别为图中红色、黑色、绿色矩形框位置;避障换道后,系统规划出沿着车道中心线,控制车辆沿着该车道中心线继续行驶,而动态障碍物继续沿着原车道车辆中心线继续行驶。

图6 动态障碍物不同速度下的避障路径规划及跟踪行驶曲线

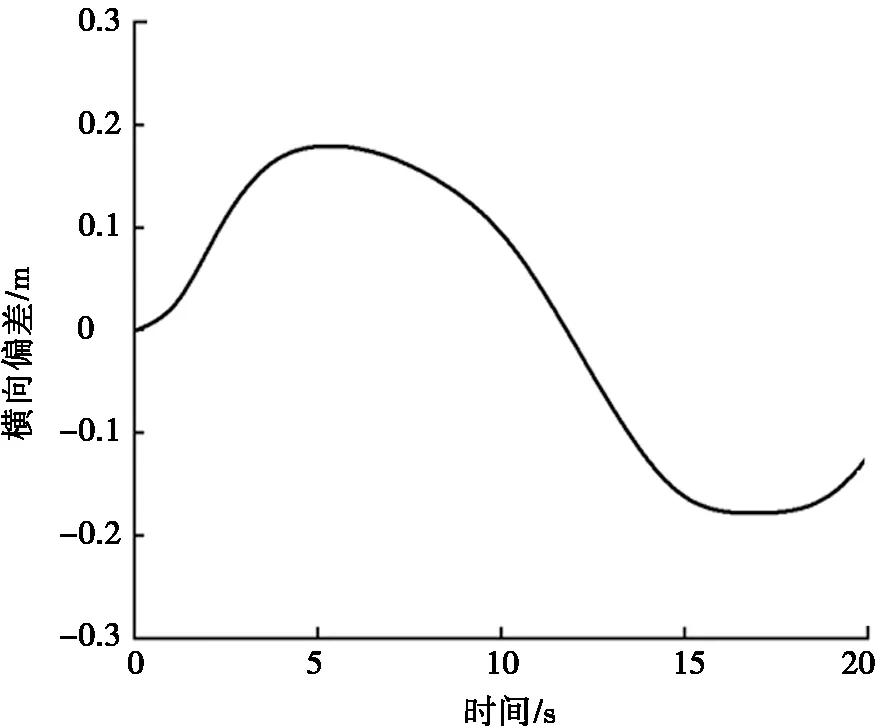
图7 车辆行驶路径与规划路径的横向偏差

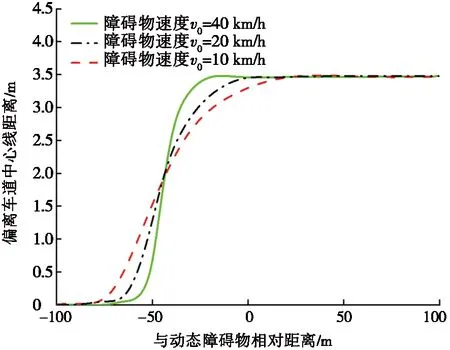
图8为智能车辆与动态障碍物的相对距离与偏离车道中心线、横摆角的关系曲线图。从图8a和图8b可以看出:随着动态障碍物速度的增加,智能车辆与障碍物间的相对速度越来越小,此时系统控制车辆跟踪所规划路径的横摆角也在减小。

(a) 偏离车道

图9为动态障碍物不同速度下的路径跟踪结果图。从图9可以看出:障碍物速度为10 km/h时,车辆前轮转角、横摆角速度、质心侧偏角、侧向加速度的最大值分别为0.026 1 rad、0.071 7 rad/s、0.002 4 rad、0.518 m/s2;障碍物速度为20 km/h时,车辆前轮转角、横摆角速度、质心侧偏角、侧向加速度的最大值分别为0.023 8 rad、0.069 1 rad/s、0.023 9 rad、0.473 m/s2;障碍物速度为40 km/h时,车辆前轮转角、横摆角速度、质心侧偏角、侧向加速度的最大值分别为0.022 9 rad、0.062 7 rad/s、0.001 9 rad、0.404 m/s2,各参数曲线变化平稳,没有出现较大波动,其值均处于合理范围内,并且随着障碍物速度的增加,车辆的前轮转角、横摆角速度、质心侧偏角、侧向加速度的值在减小。因为障碍物速度的增加,智能车辆与障碍物间的相对速度在减小,进而智能车辆受到的势场作用减弱,致使系统规划的路径更为平滑,系统能够平稳、精确地控制车辆进行路径跟踪。

(a) 前轮转角

5 结束语

本文考虑智能车辆的路径规划,将改进APF建立的势场模型函数引入到MPC的目标函数和约束中,设计了基于MPC和改进APF的避障路径动态规划器。经过仿真验证分析,避障路径规划器在跟踪规划路径过程中最大横向偏差约为0.170 m,证明改进的APF和MPC能够在动态障碍物环境下合理规划出安全的避障路径。同时随着障碍物速度的增加,车辆的前轮转角、横摆角速度、质心侧偏角、侧向加速度的值在减小,因此基于MPC和改进APF的避障路径动态规划器规划的路径更为平滑,系统能够平稳、精确地控制车辆进行路径跟踪。

本文针对智能车辆的跟踪控制,建立了基于模糊MPC的车辆横向路径跟踪控制器,与传统MPC相比,模糊MPC路径跟踪控制方法可使控制输出平滑,更加满足车辆的稳定性,同时模糊MPC控制器在干燥路面时最大横向偏差减少19.14%,在湿滑路面下横向偏差减少0.55 m,因此在不同路面下模糊MPC能更有效协调路径跟踪准确性和横向稳定。