基于剪切稀化模型的三通减阻数值模拟

张志，张浩，2，∗，李茂林，石若冉

(1.山东建筑大学热能工程学院， 山东 济南 250101；2.山东省绿色建筑协同创新中心，山东 济南 250101)

0 引言

在当今环境污染与能源危机的大背景下，节能减排已经成为了我国实现“双碳”目标的重要方式，近年来有学者认为节约能源已经成为了继煤炭、石油、天然气和电气之后的第五大能源[1]，从侧面反映了节约能源对于解决能源危机的重要性。 我国建筑能耗在总能耗中占比约为45%，其中在供热管路中，管道输运阻力约占供热量的30%。 为了减少碳排放、降低能源消耗，有必要减少供热管路的输运阻力[2]。 三通作为供暖管路主要的分流和汇流部件，对于增加管道阻力有着重要的影响。 当流体流经三通处时，由于不同速度流体的冲击混合、流量变化以及壁面影响，会形成弯曲的流线和涡旋区，进而导致流体流动过程中的压力和能量损失，增加了输运过程中的能耗[3]。

供热管道中的减阻方式，可以分为非光滑表面减阻(如沟槽减阻、凹坑减阻、仿生表面减阻)、疏水表面减阻以及添加减阻剂减阻[4]。 其中，以添加减阻剂减阻最为方便、减阻效率最高。 Toms 发现在管道中添加少量的高分子聚合物可以起到减阻效果(称之为Toms 效应[5])，后来有研究人员发现在管道中添加表面活性剂同样可以起到减阻的效果。 高分子聚合物具有添加微量便可减阻的特点，对环境影响小，但由于其易降解、不耐剪切，在空调及供暖管路中难以发挥作用，而表面活性剂抗剪切能力强，即使失效再次满足条件仍可恢复减阻效果，可以更好地适应空调/供热管路的减阻。 Kotenko 等[6]开展了减阻表面活性剂在区域供冷的实验研究，选用了针对不同温度范围的水溶液开发的两种减阻产品进行实证，发现两种减阻率工作温度范围在5 ～55 ℃时，其最大减阻率在60%～80%之间。

为了探究表面活性剂溶液减阻机理，不少学者针对其流变特性展开研究。 谢程程等[7]测量分析了混合比例为1 ∶1 的十六烷基三甲基氯化铵(Cetyltrimethyl Ammonium Chloride，CTAC)和水杨酸钠(Sodium Salicylate， NaSal)溶液流变特性，发现减阻溶液黏度变化与质量浓度及剪切率大小相关。 莫伟南等[8]对CTAC 溶液进行了流变实验测量，发现减阻溶液剪切黏度随剪切率变化过程大致分为剪切稀化、剪切增稠和二次剪切稀化3 个阶段，剪切稀化模型Carreau－Brid 和黏弹性模型Giesekus 均能较好地拟合形成剪切诱导结构之后的流变特性曲线。

文章以汇流三通为研究对象，采用非牛顿流体模型中的剪切稀化Carreau－Bird 模型，模拟添加表面活性剂CTAC/NaSal 溶液后三通管内的流动现象，对比纯水与CTAC 溶液不同雷诺数下模拟结果，通过对减阻率、速度、湍动能变化及涡旋结构变化探究管内减阻特性。

1 数值计算方法

1.1 物理模型

汇流三通几何模型如图1 所示，D 为管径；Inlet1 和Inlet2 分别为两个进口，Outlet 为出口；a－a、b－b、c－c 分别为进口1、2 及出口上的截面；x、z 为坐标轴方向。 管径D 设置为20 mm，为了使流动进入充分发展阶段，并且出口不影响汇流后的流动，设置Inlet1 进口段距离为6D，Inlet2 进口段距离为4D，Outlet 出口段距离为6D。

图1 汇流三通几何模型图

1.2 数学模型

流体流动的连续性方程、动量方程[9－10]分别由式(1)和(2)表示为

式中ρ 为流体密度，kg/m3；t 为流动时间，s；ui、uj为不同方向的速度，m/s；p 为压力，N/m2； xi、xj为不同方向的位移，m；μ 为流体黏度，N·s/m2；fi为流体质点的单位质量力，N。

汇流三通中的流动特性比较复杂，存在流线弯曲、涡旋及二次流现象。 相比k 模型以及k－ε 模型，雷诺应力模型(Reynolds Stress Models， RSM)更细致地考虑了流动过程中流线弯曲、旋转、剪切应力快速变化及局部涡旋现象，可以更加精准地预测复杂流动。

RSM 湍流方程由式(3)表示为

湍动能k 的方程和耗散率ε 的方程分别由式(4)和(5)表示为

式中Pij为剪应力产生项；Gij为浮力产生项，对于不可压缩流体，其值为零；μt为湍动黏度，N·s/m2；δij为克罗内克函数符号，当i 和j 两个指标相同时，δij＝1，当指标不同时，δij＝0；经验常数取默认值，C1＝1.8、C2＝0.6、C1ε＝1.44、C2ε＝1.92、C3ε＝0.09、σk＝0.82、σε＝1。

表面活性剂CTAC/NaSal 溶液黏度模型采用非牛顿流体模型中的Carreau－Bird 模型。 表面活性剂的剪切稀化特性是其减阻的重要特性之一，李恩田[11]、张红霞[12]分别通过验拟合出CTAC 溶液部分浓度及温度下Carreau－Bird 模型参数，并验证了数值模拟与实验结果。

Carreau－Bird 模型由式(6)表示为

1.3 参数设置及边界条件

模拟选择稳态求解器，采用压力修正(Pressurebased)的求解方法，通过压力耦合方程组的半隐式方法(Semi － Implicit Method for Pressure Linked Equations， SIMPLE)耦合压力及速度，对于收敛残差值设置，连续性方程设为10－5，其耦合方程设为10－6，并监测截面a－a、b－b、c－c 上的总压值，当总压值稳定不变时认为模拟结果满足要求。

边界入口条件为速度进口(Inlet)；出口为压力出口(pressure-outlet)，其值取默认值0；壁面采用无滑移壁面(wall)条件。

计算域中的流体分别采用采用牛顿流体纯水与表面活性剂CTAC/NaSal 溶液，其中纯水的物性参数为ρ＝998.2 kg/m3、μ ＝1×10－3N·s/m2。 溶液中CTAC 的浓度较小，除黏度变化外，其他物性参照水的物性，黏度大小通过Carreau－Bird 表征，文章假定表面活性剂流动已经进入稳定剪切黏度状态下，模型相关参数根据文献[11]得到，取η0＝7.392 2 mPa·s、η∞＝0.586 1 mPa·s、λ＝0.0147 1、n＝0.312 3，描述质量浓度为200 mg/L 的CTAC 溶液。

1.4 网格无关性与模型验证

网格质量和数量直接决定了数值计算的时间和精度，理论上网格越密，计算结果越精准，但所需计算资源、时间也越多，所以在进行网格划分时不可能无限制加密网格。 为了确定对计算结果影响最小的网格密度，文章选取了4 种不同尺寸的网格方案，网格数量分别为65 万、207 万、309 万、404 万(分别对应方案1、2、3、4)。

选取雷诺数为20 001.2 时，CTAC/NaSal 溶液在以上4 种网格方案中的模拟结果，如图2 所示，网格数较少的方案1 与其余方案相比，在中轴线上静压值变化相差较大，方案2、3、4 基本吻合，方案2(207 万)已满足计算精度要求。 选取网格方案2，划分三通的结构化网格，通过O－Block实现对圆柱结构的更好适应，加密管壁边界层处的网格，边界层第一层网格厚度大小设置为0.01 mm，网格增长率为1.15，得到的网格数的207 万，而网格质量则在0.86～1之间。 网格划分如图3 所示。

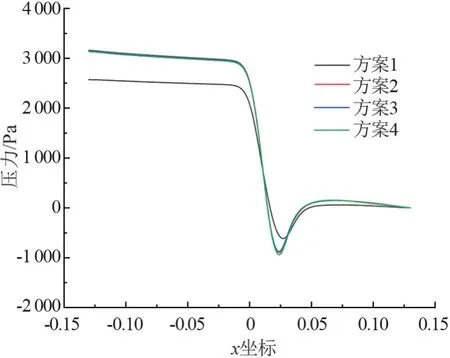
图2 网格无关性验证图

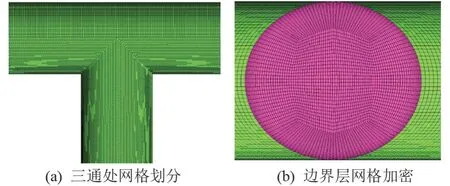
图3 方案2 局部网格图

为了验证所采用的Carreau－Bird 模型参数是否合适，选取管径D 为20 mm、长度为13D 的直管模型，模拟雷诺数为20 000 时纯水和CTAC 溶液的管内流动，通过比较纯水与CTAC 溶液在湍流近壁面流场参数变化来判断是否发生减阻效应。

采用无量纲离壁距离与无量纲平均轴向速度表达方法，其中无量纲离壁距离y＋的计算公式由式(7)和(8)表示为

式中y 为距离壁面长度，m；uτ为摩阻流速，m/s；τw为壁面平均剪切应力，Pa； Δp 为进出口压差，Pa；L为直管长度，m。

无量纲平均轴向速度U＋由式(9)表示为

式中U 为直管内流速，m/s。

无量纲平均轴向速度与无量纲离壁距离关系曲线如图4 所示。 对于牛顿流体，迪恩(Dean)平均轴向速度分布曲线计算式由式(10)和(11)表示为

图4 无量纲平均轴向速度分布曲线图

对于减阻溶液，高分子聚合物在对数区的Virk平均轴向速度渐近线计算式[13]由式(12)表示为

由图4 可知，纯水的平均轴向速度在边界层上的变化，比较符合Dean 曲线，在黏性底层与对流区轨迹基本吻合，CTAC 溶液在黏性底层区域的变化和纯水变化相同，随着y＋的增加，CTAC 溶液的无量纲平均轴向速度上升变缓，略小于Virk 曲线，位于Virk 曲线与Dean 对数区曲线之间。 在黏性底层和对数区，CTAC 溶液无量纲平均轴向速度曲线斜率大于纯水，在对数区曲线向上偏移，与添加剂减阻规律一致，因此可以认为该模型参数能够模拟出表面活性剂在管道内的减阻效应。

1.5 关键参数计算

根据伯努利方程，可以得到不同管路之间的局部阻力系数计算公式，分别由式(13)和(14)表示为

式中ξ01、ξ02分别为a、c 管段之间与b、c 管段之间的局部阻力系数；p1、p2、p3为在截面a、b、c 的平均静压，Pa；u1、u2、u3为a、b、c 管段的平均流速，m/s；λ1、λ2、λ3分别为a、b、c 管段的摩擦阻力系数[14]；L1、L2、L3分别为截面a、b、c 到原点的距离，mm。

牛顿流体纯水的主管雷诺数Re 由式(15)表示为

对于表面活性剂溶液，黏度取决于剪切速率，无法直接应用牛顿流体的计算方法，因此采用文献[15]的方法，通过特征剪切速率下的黏度计算，由式(16)和(17)表示为

减阻率RD的计算由式(18)表示为

式中ξ、ξ′分别为纯水和CTAC 溶液的局部阻力系数。

2 结果与分析

2.1 减阻率规律

三通管路与直管路在结构上相差较大，在加入CTAC 减阻溶液之后可能存在不同的减阻规律，比如两者减阻变化过程不同、减阻最值的不同以及减阻最值发生的雷诺数不同。 通过模拟同等管径及长度下的三通与圆直管，得到减阻率随Re 的变化规律，如图5 所示。 可以发现三通与直管的减阻率变化趋势是一致的，呈现随雷诺数先增大后减小的规律。 但两者的最大减阻率以及发生最大减阻的雷诺数范围存在差异，直管最大减阻雷诺数约在40 000，最大减阻率＞45%，这个结果与实验数据[9]是一致的；三通减阻最大值雷诺数约在10 000，并且仅能达到约30%。 相对于直管，三通中可能存在部分区域，而添加CTAC 溶液可能无法完全发挥其减阻效果，因而导致减阻效果不佳。

图5 CTAC 溶液减阻率随Re 数变化图

根据减阻率的变化情况，可以将减阻过程分为3 个区域，分别为不完全减阻区Ⅰ(Re＜第一临界雷诺数Re1，减阻率＜0)、完全减阻区Ⅱ(Re1≤Re≤第二临界雷诺数Re2，减阻率＞0)以及过减阻区Ⅲ(Re＞Re2，减阻率＜0)。 圆直管在雷诺数＜12 000，减阻溶液即处于不完全减阻区Ⅰ，此时减阻率＜0，对于整个管路来说，添加减阻剂增加了阻力，随着雷诺数的减小，管道增阻明显。 这主要是由于处于此雷诺数区间，剪切应力很小，没有形成剪切诱导结构，无法发挥其减阻效应。 三通管不存在不完全减阻区Ⅰ，由于三通流体间的冲击与壁面分离，即使是在较小的雷诺数下，仍能形成剪切诱导结构。 在稍微增加雷诺数的情况下，便达到最大的减阻效果，随雷诺数增加，达到过减阻区域Ⅲ，溶液中的剪切诱导结构被破坏，导致不再减阻。

2.2 流速变化规律

2.2.1 轴向速度分布

雷诺数为20 001.2 时，主管中轴线上的纯水和CTAC 溶液轴向速度变化如图6 所示，其中横坐标x通过管道直径D 做无量纲化，纵坐标轴向速度U 通过断面平均流速Ub做无量纲化。

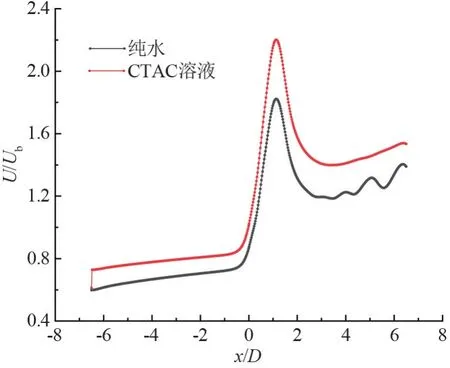
图6 Re＝20 001.2 时轴向速度变化图

随着进口距离不断增加，速度值逐渐增加，直至三通支管处，主、支管发生汇流，流量增加，导致区域内速度急剧上升；同时由于两股流体合并，伴随着剧烈的湍流运动，能量耗散，流动阻力增加，在汇流之后形成涡旋区域，导致速度不断降低，速度下降到一定值后稳定在原始速度的2 倍。 比较纯水和CTAC溶液可以发现，CTAC 溶液的无量纲化速度始终处于纯水之上，这表明CTAC 溶液起到了提高流动速度的作用；在出口段的无量纲速度值，纯水处于上下波动，表现为较强的湍流状态，CTAC 溶液较为恒定，表现为稳定的层流状态。 出口段速度分布，CTAC 溶液相比于纯水的出口速度分布较为均匀，并未出现速度波动分布现象，表明添加CTAC 溶液可以促使出口段流动从湍流状态向层流状态转变。

2.2.2 流速等值线分布

Re＝6 000.2 时，三通管路对称中心面(y ＝0)上纯水和CTAC 溶液的速度分布云图如图7 所示。 汇流三通主要阻力来源于两股不同流速的流体混合紊流冲击产生的损失，以及汇流之后在内管壁分离形成的回流区，该回流区通常伴随着强烈的涡旋现象。在进口1 和2，流体以0.5 m/s 的速度进入管路，在汇合处左侧靠近壁面区域，产生一个低速区，这是流体偏转的向心力导致的。 在汇合处，两股流体相遇，速度增加，分层明显。 在汇合后管道内侧壁面(以靠近支管侧为内侧)附近产生了一个涡旋区，在外侧壁面处产生一个高速流动区，这主要是由于流体偏转脱离壁面所引起的，涡旋区的大小在一定程度上反映了三通的阻力。

图7 Re＝6 000.2 时，y＝0 平面上的速度分布云图

从整体的流速分布来看，CTAC 溶液减小了低速区的范围，增大了管道外侧高速流动区的范围，改变了三通管内流速分布，减少了能量耗散，实现了减阻，但也增大了涡旋中心区的速度，提高了该区域的湍流运动，可能会使阻力增加。

2.3 湍动能变化规律

2.3.1 沿程湍动能变化规律

为了研究三通内沿程湍动能变化规律，分析不同雷诺数下纯水与CTAC 溶液在主管轴线上各断面的沿程湍动能变化，结果如图8 所示。 可以看到，在相同雷诺数下，多数截面CTAC 溶液的湍动能更小，并且在减阻率较大的雷诺数下(20 000～40 000)，两者湍动能差值更大。 在进口段(x ＝－0.15 ～0 m)CTAC 溶液相对于纯水湍动能降低约为50%～75%，说明减阻溶液实现了对湍流的较好的抑制作用，处于更好减阻雷诺数的流动中，对湍流运动的抑制越明显。 而在图8(a)较小雷诺数和图8(d)较大雷诺数下，纯水和CTAC 溶液的湍动能差别较小，在进口段湍动能仅降低了10%～25%，这正好与CTAC 溶液在三通管路的减阻率随雷诺数变化相对应，较大或较小的剪切力都会降低减阻剂的减阻效果。

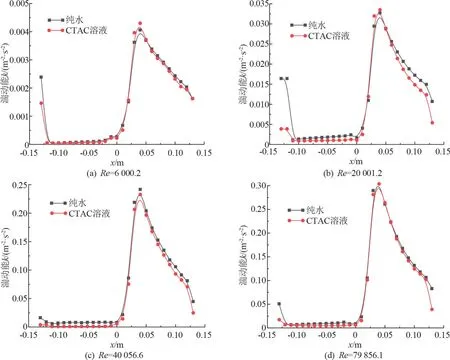
图8 不同雷诺数下纯水和CTAC 溶液沿程湍动能分布图

由图8(b)可以看出，在x ＝0 m 处湍动能急剧增加，此时CTAC 溶液湍动能相对于纯水湍动能提高约8.5%，由于汇流与壁面分离效应，流动的剪切应力较大，超出CTAC 溶液减阻范围，添加减阻剂导致湍动能增加，随着流动的发展，远离涡旋区后，减阻剂逐渐恢复减阻效果。

2.3.2 径向湍动能分布规律

由于在轴向湍动能分析时，x ＝0 m 处(流动涡旋区)CTAC 溶液的湍动能值大于纯水湍动能值，因此选取Re＝20 001.2 时纯水和CTAC 溶液分别在截面x ＝0.02、0.03、0.04、0.05 m 处径向湍动能分布图，分析径向湍动能变化及在不同截面上径向湍动能发展，如图9 所示，其中d 为径向方向上的坐标。 由图9(c)可以发现湍动能最大值时发生在管道中心靠内侧的位置(d/D ＝－0.1 处)。 外侧壁面(d/D ＝0.5 处)纯水的湍动能大于CTAC 溶液；随着离壁面距离增加，湍动能不断降低，此时纯水和CTAC 溶液的湍动能相差较小；接近涡旋区(d/D ＝0 附近)时，湍动能急剧增加，此时CTAC 溶液的湍动能是大于纯水的；离开涡旋中心区后(d/D＜－0.2)，湍动能大小表现为CTAC 溶液小于纯水。 由此可知，在高速流动区(d/D≥0.2)，CTAC 溶液起到了减阻的效果，并且减阻主要发生在近壁面附近；在涡旋中心区(－0.2≤d/D＜0)，表现为增阻，此时加入CTAC 导致流动的湍动能增加，涡旋区的剪切应力过大，CTAC分子无法形成剪切诱导的网状结构，而是无序的分布在溶液中起到阻碍作用。

图9 Re＝20 001.2 时纯水和CTAC 溶液径向湍动能分布图

在内侧壁面处(d/D＜－0.2)，CTAC 溶液与纯水的湍动能处于发展阶段，随着流动的进行，CTAC 溶液的湍动能逐渐小于纯水，减阻剂恢复减阻效应。由此可知，添加CTAC 时，减阻主要发生在壁面和远离涡旋中心区的近壁面，而涡旋中心区增加了阻力，由于整个流动中涡旋中心区的范围较小，且增阻效果不明显(湍动能增值仅为8.5%)，因此添加CTAC整体表现为减阻效果，但达不到直管段中的减阻率。

2.4 涡旋结构分析

2.4.1 涡量云图

流体流动过程中，涡旋结构的产生会增加流动阻力和能量耗散，向纯水中添加表面活性剂溶液进行减阻，同样会对流动过程中的涡旋结构产生影响。通过分析涡旋结构变化，可以对添加CTAC 减阻机理有更深的理解。 因此，文章采用第二代涡识别方法中的Ω 准则[15]，计算了当Re＝20 001.2 的纯水和CTAC 溶液的涡量，得到的涡量云图如图10 所示。

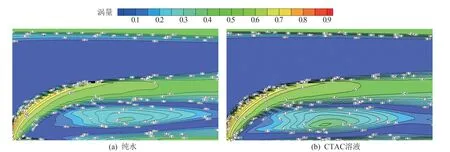
图10 纯水和CTAC 溶液局部涡量云图

比较分析轴向及径向湍动能大小，可以发现位于汇流之后的涡旋区，CTAC 溶液减阻效果并不好，因此涡量云图选取的是三通管内流动的下半段区域。 通过对比涡量分布，可以发现相比于纯水，CTAC溶液的较大值涡量在外侧(上)壁面与内侧(下)壁面区域范围变小，在涡旋区与高速流动区交界处附近变化不大，而在涡旋中心区域范围增大，这种变化与之前所分析的径向湍动能变化是一致的。

2.4.2 Q 准则涡旋结构

湍流结构通常通过具有旋转运动的涡旋结构表示。 涡旋结构的旋转大小可以通过Q 准则表示[15]。Q 准则能较好的表达涡大小，但容易受到壁面剪切层影响，同时Q 阈值的选取也会影响结构的显示。根据Q 值特征及三通管内流动特性，选择了Q 分别为200、500、1 000 的等值面，用速度云图体现，得到的Re＝20 001.2 下的纯水与CTAC 溶液局部涡旋结构如图11 所示。

图11 Q＝200 等值面下流体速度分布图

两种溶液的速度分布都比较符合汇流之后的流动轨迹，选择Q＝200 的等值面来代表涡旋结构是可行的。 从图11 可以得到，在三通管内流动的下半段，涡旋结构主要出现在内侧壁面(靠近支管侧)。外侧壁面流动主要以剪切为主，旋转为次，因此在管道外侧壁面处并未出现或少量出现涡旋。 大的涡旋结构出现于流动汇流后，尤其是靠近内侧壁面附近。汇流初始涡旋结构较大，随着流体流动发展，大尺度涡旋结构逐渐破碎分离，形成小尺度涡旋结构，最终在靠近出口处涡旋结构几乎消失。 通过对应速度可以发现，涡旋结构较大的区域有着较大的速度。 与CTAC 溶液相比，纯水整体涡旋结构范围更大，同时发展长度更长，涡破碎过程中，纯水中涡破碎分离距离更远，并且小尺度涡的数量下降显著。 在涡旋中心区，两者的涡旋结构差别不大，管内加入CTAC 溶液在此处并未起到抑制涡旋大小的作用，因而在较大剪切力的涡旋中心区，CTAC 溶液表现的特性与牛顿流体纯水并无差异。

图12(a)是当Q 值为500 时的流体速度分布，其整体涡旋结构范围小于Q ＝200 的结构(如图11所示)，这说明的旋转强度有所下降。 在涡旋中心区，图12(a)中纯水及CTAC 溶液涡旋结构大小与图11 差异不大，这是由于流动汇流区整体剪切力较大，在强剪切力下，Q 值选取具有更大的范围，其对阈值变化敏感度降低。 而在涡破碎分离区，图12(a)中纯水及CTAC 溶液涡旋结构大小与图11 呈现较大差异，比较纯水涡旋结构变化，可以发现其密集程度明显降低，流向涡与展向涡数量在一定程度上减少。 对于低剪切力的小尺度涡旋，Q 准则捕捉能力较弱，对阈值的依赖性更大。 同样的，图12(b)在选取Q 值为1 000 时，涡旋结构更小且更加分散。

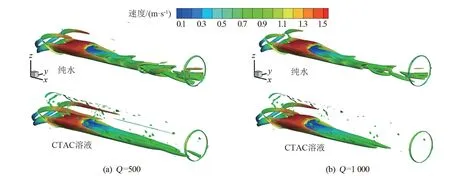
图12 Q＝500 及Q＝1 000 等值面下流体速度分布图

尽管对于小尺度涡旋显示的范围不同，但通过对比相同Q 值下纯水和CTAC 溶液涡旋结构大小，3 种Q 值等值面图也呈现了相同的规律。 由此可知，加入CTAC 溶液影响了管内涡旋结构，降低了小尺度涡旋的产生和涡发展长度，尤其对于出口段的涡旋结构，有效地起到了抑制作用，使其朝层流方向转变。

3 结论

文章通过CFD 软件模拟了CTAC 溶液的剪切稀化特性在三通管内产生的减阻效应，通过将CTAC 溶液与同工况纯水模拟结果相比较，得到以下结论:

(1) 与直管相比较，三通最大减阻率较低，在低雷诺数以下不存在减阻率＜0 的区域，随雷诺数增加减阻率在达到峰值后，很快降至接近零。

(2) 添加CTAC 会改变三通管内流速分布。CTAC 溶液中的低速区范围变小，高速流动区范围变大，同时涡旋中心区存在速度增加的现象。 相同雷诺数下CTAC 溶液的主管轴向无量纲速度大于纯水，在流动出口段CTAC 溶液的速度更加稳定，出口段湍流流动趋近于层流化。

(3) 湍动能降低并非发生在整体区域，对于涡旋中心区，CTAC 溶液湍动能是增加的，在远离涡旋区及近壁面处小于纯水的，在涡旋区内侧不同截面处呈现不同的变化。

(4) CTAC 溶液涡旋结构发生改变。 溶液中整体涡旋结构变小，小尺度涡数量下降，壁面以及近壁面处涡量减少，涡旋中心区的涡量增加，其减阻效应主要发生在壁面附近和远离涡旋中心区的近壁面。