基于动态投资的鲁棒契约设计与应用研究
甘 柳,夏 鑫
(1.闽江学院 新华都商学院,福州 350108;2.中南财经政法大学 金融学院,武汉 430073)
在公司金融中,企业投资效率是学术界和实务界共同关注的核心问题之一。经典理论分析表明,在完美资本市场假设下,企业仅对净现值为正的项目进行资本投资。然而,现实中外部金融市场摩擦会扭曲企业投资决策,其中委托代理问题就是市场摩擦的一个重要来源。由于所有权和经营权分离,外部投资者往往会怀疑高管的谋私(或努力不足)动机,导致企业不能像预期那样以足够低的成本获得资本,从而导致非效率投资。而委托人通过薪酬契约使代理成本最小化,这为研究代理问题对企业投资效率的影响机制提供了渠道。对此,国内外学者从最优薪酬契约的角度进行了大量研究。
近年来,随着契约理论的发展,学者们基于连续时间金融模型探讨了不同市场摩擦因素下的动态代理问题。这些理论将外部融资成本视为内生因素,构建了动态薪酬契约影响企业非效率动态投资决策的理论分析框架,其中代表性成果主要有De Marzo等[1]和Ai等[2]。前者结合新古典投资q理论构建了内生投资的动态契约模型;后者引入管理者与股东双方的有限承诺,构建了小企业与大企业差异化投资策略的动态契约模型。已有文献主要从3个方面对文献[1-2]的研究进行了推广:①通过引入不同的市场摩擦因素构建动态契约模型。Chi等[3]引入资本存量的随机冲击,构建动态代理模型并研究不同规模企业的投资行为;Li等[4-5]通过引入指数型生产函数,构建了基于投资的动态契约模型;Bolton等[6]研究了动态契约模型与动态投资q理论模型的对偶问题1)实际上,企业动态投资q 理论模型研究始于Jorgenson[7],随后的拓展研究包括文献[8-11]等系列研究,国内的研究主要有刘琦等[13]以及甘柳等[14]。②同时考虑高管努力和冒险的双重控制权构建动态契约模型。甘柳等[14]研究了动态契约下长期动态投资的跳风险问题。③通过融入高管短期和长期努力行为构建多重任务下的动态契约模型。这一方面以Gryglewicz等[15]的研究为代表。
上述动态代理契约研究都遵循传统理性预期假定2)国内学者[16-18]从静态投资的角度考虑动态契约,即认为委托人和代理人对企业收益流的不确定性拥有共同信念。然而,Ellsberg[19]悖论以及Gilboa等[20]的研究都指出决策是否有效取决于两个方面:参数估计误差导致决策模型的参数不确定性问题和资产价值分布函数设定误差导致决策模型的不确定性或误设问题。Hansen等[23]也指出,决策者对市场的模糊性是模型不确定性产生的根源,而模糊性的出现是由于决策者对信息掌握不足。在现实中,决策者往往是模糊厌恶的[24],模糊信念的存在限制了委托人对信息处理的时效性,同时对信息获得的容量也产生了约束。
鉴于此,近年来,结合鲁棒最优化[21]和随机动态规划[22]等方法的鲁棒决策模型及其在企业经营决策中的应用发展较迅速。代表性的有文献[25-27],通过引入委托人对企业单位产出平均增长率的模型不确定性,分别从不同视角构建了鲁棒契约模型,并分析了相应的企业经营决策问题。随后,Zhao[28]在Gryglewic等[15]的基础上研究了两个布朗运动下的鲁棒契约设计问题。与这些文献相区别,本文基于De Marzo等[1]的理论分析框架,考虑委托人对企业资产波动率的模糊厌恶,对鲁棒契约设计及企业动态投资决策问题进行研究。具体地,从委托人不相信代理人报告的收益流的概率测度出发,将委托人波动率模糊厌恶视为内生因素。同时,引入代理人的努力成本,进而通过代理成本最小化来设计鲁棒契约。传导机制表明,委托人会通过薪酬契约设计将模型不确定性转移给代理人,从而对企业最优动态投资决策产生影响。在此基础上,进一步分析委托人波动率模糊对企业证券定价、托宾q、股权溢价以及信用价差的影响。
本文数值分析结果表明,波动率模糊下的鲁棒契约在委托人和代理人之间产生异质信念,使得委托人认为企业现金流的波动率高于真实波动率。特别地,当企业处于财务困境时(现金流接近清算边界),模糊厌恶的委托人认为波动率相对更高,并由此形成更严重的投资不足。同时,当企业面临较高的不确定性时,处于财务困境的企业进行投资产生的边际价值较小,这与Eisdorfer[29]的实证结论相符。此外,波动率模糊的存在会降低股东价值、契约规定的投资率以及企业平均q。最后,通过融入波动率模糊性厌恶,本文发现股权溢价和信用价差正相关,且两者都与企业的投资率呈负相关,这与Hou等[30]和Chordia等[31]的实证研究结论一致。
本文可能的贡献主要体现在3个方面:
(1) 首次从动态投资视角分析了波动率模糊的鲁棒契约问题。作为公司金融领域的重要问题之一,动态契约研究已经产生了丰富的研究成果,但已有研究主要基于理性预期这一前提假设。本文考虑委托人波动率模糊厌恶3)由于我国上市公司普遍存在“一股独大”、股权分割等现象,故考虑股东(委托人)的异质信念假设更合理,利用连续时间金融模型对企业动态投资决策、证券估值等进行分析。同时,给出了异质信念下波动率的时变效应,为后续相关研究提供了理论借鉴。
(2) 为理解企业非效率投资(特别是投资不足)问题提供新的可能性分析机制。已有研究从不同角度分析企业的非效率投资决策问题,包括委托代理理论、信息不对称理论、资本结构理论以及公司治理等[32]。但是,鲜有文献在委托代理理论框架中,从决策者的模糊信念角度进行分析。如前文所述,委托人的异质信念会扭曲企业资产的波动率,从而导致其投资扭曲,这为理解企业非效率投资问题提供了新的思路。
(3) 本文分析了波动率模糊厌恶对股权溢价和信用价差的影响,并进一步分析了他们与企业投资率的相关性。这拓展了相关理论研究,也能对相关实证分析提供更丰富的理论基础[33-34]。
1 基本假设与鲁棒契约
1.1 企业生产与波动率模糊
本文基于新古典投资q理论框架构建基本模型[1-2]。假定企业采用实体资本进行生产,其中,记{K t}t≥0为在任意时刻t企业的资本存量水平,{A t}t≥0表示企业单位资本存量的累积产出。由于所有权和经营权的分离,委托人(股东)授权管理者(代理人)行使企业的经营决策权。因此,为刻画代理冲突对企业产出的影响,记a={a t}t≥0为管理者的努力水平,其中,a t∈{0,1}。令Pa表示由a引致的概率测度[14],在Pa下,假设单位时间内企业单位资本存量的产出水平{dA t}t≥0,其服从如下扩散过程:
进一步,假设企业资本积累过程满足如下动态方程[1]:
式中:常数δ(≥0)为资本折旧率;随机过程{I t}t≥0为在任意时刻t企业的投资水平,所产生的资本调整成本为G(I,K)4)该成本包括买入/卖出资本的基础价格成本和投资摩擦成本。参照文献[1],假设G(I,K)是投资水平I与资本存量K的一阶齐次函数,即G(I,K)=g(i)K,其中,i=I/K为投资资本比,g(i)为单调递增的凸函数。在本文模型中,设g(i)=i+θi2/2,其中,θ刻画了资本调整成本的摩擦强度[1]。假设企业在任意单位时间内的运营收入与资本存量成比例,其单位时间内的运营净收入{dY t}t≥0可表示为
假设委托人不相信代理人汇报的收益流概率分布Pa,因此,委托人会扭曲Pa然后进行最优契约设计。参考Maccheroni等[35]的研究,本文给出基于生产模型的波动率模糊鲁棒契约问题。定义可测过程v={v t}t≥0,将式(1)改写为
决策者通过选择v来最小化自身效用,但同时付出成本Ψ(v,K),其中Ψ(·,K)是一个非负凸函数。由此,委托人将概率测度Pa扭曲为概率测度Pv,在概率测度Pv下是一个布朗运动。结合文献[23,35]中关于相对熵罚函数的讨论,考虑如下相对熵罚函数:
式中:log(·)为自然对数;Ψ(v,K)的形式类似于文献[23]中的稳健控制偏好;参数π控制决策者的模糊厌恶程度。
1.2 波动率模糊下的鲁棒契约
假设委托人是风险中性的,其无风险贴现利率为r。委托人基于概率测度Pv进行决策,通过设计合理的投资水平I、薪酬支付水平C以及企业清算时机T,使得代理人在追求自身利益最大化的同时,还能符合委托人的利益,进而确保代理成本的最小化。另外,在引入模糊信念后,委托人寻找最优的测度Pv,使得因概率扭曲引起的惩罚费用最小的同时,还要在最坏概率测度Pv下重新计算企业收益流。外部最优化问题表明,在给定模糊厌恶Ψ(v,K)的程度下,当最坏情形概率Pv发生时,在初始时刻委托人拟定契约Γ=
问题1鲁棒契约问题表述为:
式中,代理人的目标函数包括薪酬的现值及其付出的努力成本两个部分。参考相关文献[27],本文将代理人的努力成本设置为关于的一次函数,并与资本存量K成比例,即根据这一设置,参数λ(>0)可直观地理解为代理人努力成本的大小[27]。如果是问题1的解,则鲁棒契约Γ=
2 鲁棒契约模型的求解
2.1 鲁棒契约的解
对于任意契约Γ=
不难得到V t(Γ,X t)是一个鞅,从而由鞅表示定理可得存在一个可测过程{βt}t≥0,使得对于任意t>0,有
此时,代理人在单位时间内的增量薪酬等于现金支付dC t和未来支付价值的增量dW t之和。考虑到代理人付出的努力成本,同时为补偿其时间偏好,这个增量补偿必须平均等于(γW t+λμK t)dt。βt越大,表明薪酬支付水平越高,因而委托人会给出最低的薪酬支付水平来形成激励相容契约,此时有βt=λ5)此处隐含假设当代理人努力而付出的成本和得到的收益相等时,代理人会选择努力成立。
接下来给出委托人值函数以及最优契约的结果。将契约问题1 中委托人的连续价值函数记为F(K t,W t),该值函数与状态变量K和W有关。参考Miao等[36]的方法,可以导出F(K t,W t)满足如下汉密尔顿-雅克比-贝尔曼 (HJB)方程:
式中,F函数的下标分别表示关于对应变量K或W的一阶或二阶偏导数。借鉴文献[1]中的研究,根据委托人值函数F(K t,W t)的齐次特性,有F(K t,W t)=K tf(w t)成立,其中,w t=W t/K t。通过求导计算可得:
进一步,假定dC t/K t=c tdt,同时注意到βt=λ。将上述结果代入式(10),并去掉时间下标后可得f(w)满足如下常微分方程:
定理1在代理人最大的努力水平下,委托人的值函数在区间上满足F(K,W)=Kf(w),其中,f(w)满足如下常微分方程:
另外,最坏情形密度算子为
契约规定的最优投资率为
证明参见Miao等[36]的研究。证毕
2.2 最优情形与参数选择
本节先给出没有代理冲突(最优情形)时模型的解(下文记为FB),然后给出本文数值分析时模型参数的取值。在没有代理冲突时,委托人也需要付出努力成本λμK。根据Hayashi[9]的研究,可得最优情形下的投资-资本比iFB=I/K满足
与De Marzo等[1]的最优投资情形相比,式(17)中多了努力成本参数λ。为保证投资率是大于0的实数,参数要求保证μ(1-λ)<g(r+δ)。另外,由齐次特性,单位资本下的企业价值为pFB(w)=qFB-w,其中,qFB=1+θiFB表示最优情形下的托宾q。
参考De Marzo等[1]的研究,本文模型参数的取值如下:无风险利率r=4.6%,代理人的贴现利率γ=5%,波动率σ=0.26,单位资本清算回收率l=0.97,资本调整参数θ=2,资本存量的折旧率δ=12.5%,努力成本参数λ=0.2,单位产出的最大平均增长率μ=0.25。上述参数均为年化后的取值。将模糊厌恶参数取为π={0.1,1,∞},分别表示波动率模糊厌恶程度较高、较低和没有3种情形。
2.3 鲁棒契约的性质
图1 展示了定理1 的结果。图1(a)表明,委托人的价值函数f(w)是关于w的上凸函数,这一结论对存在与不存在波动率模糊都是成立的。而随着参数π的增加,f(w)的值是增加的,即波动率模糊程度的增加会降低委托人的价值函数,因为此时财富转移效应更加明显。此外,随着参数π的增加,契约规定的薪酬支付上边界递减,这意味着波动率模糊厌恶程度上升会导致薪酬支付时机的延迟。当f(w)的值较低时,薪酬支付上边界较高,此时推迟补偿时间是最优的,可以减少契约的终止概率。

图1 最优鲁棒契约与投资率Fig.1 Optimal robust contract and investment rate
图1(b)表明,ν*(w)2>1(π→∞时对应ν*(w)2=1),因此,在委托人模糊厌恶下认为的波动率总会大于真实波动率σ。另外,模糊厌恶产生的波动率是时变的,当企业接近清算边界时,委托人模糊波动率相对较高,这一扭曲同样会影响委托人的价值函数,使得接近清算边界时委托人的价值降低幅度较大,而远离清算边界时委托人的价值降低幅度较小。图1(c)表明,契约规定的最优投资水平i*(w)低于没有代理冲突下的最优投资水平,表现为投资不足。而随着参数π的减少,i*(w)会进一步降低,即委托人的波动率模糊会降低企业投资水平。另外,随着波动率模糊的增强,投资率对薪酬w的敏感度i*'(w)也是降低的(见图1(d))。
在波动率模糊厌恶的情况下,最优合约会在委托人和代理人之间产生异质信念。代理人完全相信基准概率模型,而委托人则认为波动率是随时间变化的,并且严格高于基准情形下的波动率。当接近清算边界时,委托人的模糊波动率相对更高,企业经营状况变得对基本业绩的冲击更加敏感,同时导致其价值和投资率降幅最大。从委托人角度来看,当企业面临更高不确定性时,其在困境情形下进行投资产生的价值较小,这与Eisdorfer[29]的实证分析一致。另外,本文的波动率模糊模型可以得到如下两个一般性的推论。
推论1定理1给出的值函数f(w)关于π是严格递增的。
证明应用Dynkin公式将价值函数写成一个积分微分算子,然后在积分符号下进行微分,并应用包络定理得到
最后利用F(K,W)=f(w)K即可得推论。证毕
推论2薪酬支付上边界关于π是严格递减的。
证明给定任意投资水平i下有
3 鲁棒契约的应用与数值分析
3.1 比较静态分析
图2(a)和2(b)给出了在π=0.1情形下代理人的努力成本λ对契约规定的最优投资率i*(w)以及最坏情形密度算子ν*(w)2的影响。首先,努力成本增加会降低鲁棒契约的最优投资率,同时使得薪酬支付边界降低(支付时机提前)。其次,努力成本对最坏情形密度算子ν*(w)2的影响是不同的。当企业接近清算边界时,较低的努力成本对应较高的密度算子ν*(w)2,意味着委托人模糊波动率相对较高;反之,当企业远离清算边界时,较低的努力成本对应较低的密度算子ν*(w)2,意味着委托人模糊波动率相对较低。因此,当代理人的努力成本较低而使得企业陷入经营困境时,委托人对代理人的怀疑程度会更高,形成更大的模糊波动率。另外,在代理人努力成本较高的情形下,随着企业远离清算边界,最坏情形密度算子ν*(w)2的下降相对缓和。
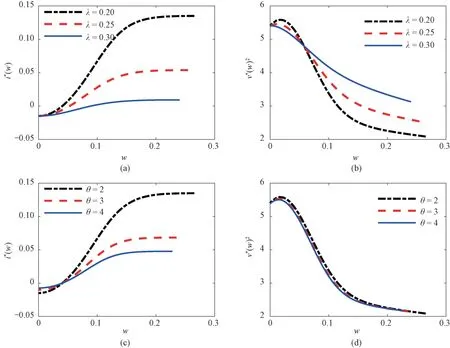
图2 努力成本和投资成本的影响Fig.2 Effects of effort and investment costs
图2(c)~2(d)给出了投资成本θ对契约规定的最优投资率i*(w)以及最坏情形密度算子ν*(w)2的影响。当远离清算边界时,投资成本增加会降低鲁棒契约的最优投资率;当接近清算边界时,较高的投资成本使得企业出售资产的速率减缓。此外,投资成本增加也会降低最坏情形密度算子ν*(w)2。
3.2 企业证券定价与托宾q
在鲁棒决策模型中,委托人所获取的信息量及精确程度往往会影响其预先确定的不确定集。而信息约束一方面会影响企业投融资等经营决策,另一方面也会直接影响企业证券的价值评估。在动态模型中,由于模糊信念变化导致信息的不断修正,故其如何影响委托人或代理人主观的企业证券价值评估? 为此,记B t、S t和M t分别为企业债务、股权和现金储备的市场价值。采用m t=M t/K t表示在区间内每单位资本的现金储备,其中,表示内生的支付边界。根据De Marzo等[1]的研究,在内部区域的演化方程为
记{U t}t≥0为股东得到的分红过程,注意到在内部区域股东分红为0。由于波动率模糊厌恶性的投资者能较好地分散风险,故企业的股权价值满足以下表达式:
对于企业债务,单位时间的债息支付为
同时,当企业清算时,债权人得到企业剩余价值l K T。于是,债务价值可以表示为
利用伊藤引理,不难得到b t=B t/K t在区间[0,]满足如下常微分方程:
根据经典的投资q理论文献,托宾平均q定义为企业市场价值与账面价值之比[1],即q t=V t/K t,其中,V t为企业总价值。因此,不难得到q t=s(m t)+b(m t)-m t,其中,s(m t)和b(m t)分别由常微分方程式(20)和(22)给出。虽然托宾边际q更准确地反映了企业未来的投资机会,但由于边际q一般是不可观测的,因而实证检验中大多采用平均q作为其代理变量。Bolton等[11]认为,在企业面临融资约束时,平均q测度投资机会具有较强的稳健性。
图3给出了不同情形下的托宾q(平均q)与现金储备m之间的关系。图中水平直线表示最优情形下的平均q,其值大小均与m无关。在代理人存在道德风险的情形下,平均q随着m的增加而增加,表现为正相关关系。根据代理人薪酬价值的演化方程式(9)和每单位资本现金储备的演化方程式(18),可以发现,企业现金储备随着过去利润的增加而增加,同时动态契约下的平均q随m的增大而增加[27]。最后,在本文的鲁棒契约模型中,随着委托人的波动率模糊变得更加严重,导致企业价值降低,从而使得平均q下降。

图3 鲁棒契约下的平均qFig.3 Average q under robust contract
3.3 股权溢价与信用价差
本节给出委托人波动率模糊厌恶下的股权溢价和信用价差分析。借鉴Miao等[36]的研究,条件预期股权溢价被定义为
式中,s(m)由微分方程式(20)及其边界条件给出。注意到当不存在波动率模糊时(即ν*(w)2=1的特殊情形),股权溢价为0;但本文模型中由于委托人的模糊厌恶产生了内生的模型不确定性(即ν*(w)2>1),由此导致了正的股权溢价。
另一方面,使用债券的信用价差CS来衡量违约风险。根据Miao 等[36]的研究,CS满足如下等式:
记D t为在违约时合同持有人得到1美元的市场价值,定义为
利用式(24)和(25)可得信用价差与债务价值的关系为
图4给出了最优鲁棒契约下模糊厌恶参数选取为π={0.1,1}时的股权溢价和信用价差分析。从图中可以看出,股权溢价和信用价差随着代理人模糊厌恶程度的增加而增加,并随现金储备m t的增加而减少。直观地,委托人的模糊厌恶使得内生信念Pv下的股权价值低于信念Pa下的股权价值。因此,委托人需要股权的预期收益溢价进行补偿,从而使得本文模型与Miao等[36]的研究不同,股权溢价和信用风险都与投资决策及平均q有关。

图4 最优鲁棒契约下的股权溢价和信用价差Fig.4 Equity premium and credit spread under optimal robust contract
此外,本文模型预测的股权溢价和信用价差都与企业的经营状况有关。当企业接近违约边界时,股权溢价和信用价差都更高,这与标准的资产定价文献是一致的[37-38],即他们发现公司的股权溢价和信用价差正相关。从经典理论模型角度,通常需要用一个高的风险厌恶系数来解释现实中较高的股权溢价。但是较高的股权溢价可能是由于模糊厌恶而不是高风险厌恶系数导致的[39]。在本文模型中,委托人是风险中性的,但是模糊厌恶激发了其与代理人模型不确定性的动机,故与风险厌恶引起的风险分担不同,模糊厌恶分担是由委托人和代理人之间的内生信念异质性引起的[40]。
本文的鲁棒契约模型预测投资较多的公司往往有较低的股权溢价、较低的信用价差和较高的现金储备。这些结果基本与文献[30-31]中的实证研究一致。本文还发现股权溢价和信用价差都与企业的投资率呈负相关关系,该结论与文献[33-34]中的实证结果一致。
4 结论
本文基于连续时间金融模型框架,构建了包含动态投资决策的鲁棒契约模型,并描述了波动率模糊下的鲁棒契约特征。鲁棒契约在委托人和代理人之间产生信念异质性,即委托人内生地认为企业现金流的波动率高于真实波动率,由此导致更严重的投资不足问题。同时,基于企业债务、股权和现金进行了模型的应用及数值模拟分析,通过参数校准,模型产生了非零的股权溢价和信用价差。研究发现:
(1) 委托人的波动率模糊厌恶降低了企业的托宾q、平均投资率和股权价值。
(2) 由于委托人波动率模糊厌恶,股权溢价和信用价差正相关,且两者都与企业的投资率呈负相关关系。
未来进一步研究可以从以下几方面进行拓展:本文仅考虑了委托人的模糊厌恶,实际上还可以进一步考虑代理人的模糊厌恶。另外,由于企业存在三级代理现象,即委托人雇佣高管,而高管雇佣工人,因而可以考虑三级代理问题中的模糊厌恶问题。

