考虑设备转换成本的MRI检查预约调度优化

林 晖,王 杉

(1.上海交通大学 安泰经济与管理学院,上海 200030;2.中山大学 管理学院,广州 510275)

核磁共振成像(MRI)检查是医生确诊患者病情的重要手段[1],目前MRI检查的等待时间长达16～36天[2],是患者得到确诊和治疗的瓶颈环节。一方面,MRI设备昂贵,平均500万元一台,最高可达2 000万元,是医院的稀缺资源,无法简单地通过增加设备数量来应对快速增长的MRI检查需求[3]。另一方面,MRI检查需针对检查部位使用特定的线圈,一般最常用的线圈就有近10种[4]。当前后两名患者检查部位不同时,更换线圈会产生较长的装卸时间和线圈损耗[3]。2018年的一项研究[5]显示,更换MRI线圈的平均时间长达13.4 min,占平均检查时间的55%,减少线圈更换次数可显著提高MRI设备的利用率。另外,一台MRI设备的线圈成本高达32万美元[6],而装卸线圈需要医务人员十分严格且精细的操作[4]。已有文献表明,频繁更换线圈会加速线圈损耗,导致线圈故障,带来高昂的维修甚至重新购置的费用[4,7]。在实践中,许多医院采用先到先服务的预约规则[8-9],但由于患者检查需求的异质性,大大增加了线圈的装卸次数,产生了非常高的转换成本。目前,已有医院通过建立MRI预约规则来减少更换线圈的次数[4],如使用固定的日期或时间段来检查特定部位[2,4],从而降低更换线圈带来的转换成本。但这又会影响患者预约的灵活性,使得MRI设备空置、患者长时间等待,导致医疗资源浪费、患者满意度降低。因此,如何对MRI检查预约进行合理的调度,在及时满足患者需求的同时,降低更换线圈带来的转换成本,是一个亟待解决的重要问题。

关于医院预约调度的文献大多以尽快满足患者需求为目标,同时考虑所消耗的资源成本。许多文献考虑了患者爽约[10-14]、患者到达不及时[15]、未预约患者[16]、随机服务时间[17]、医患匹配度[18]等因素,但很少考虑到MRI设备的特殊性,即服务不同类型患者时会产生转换成本[3]。潘兴薇等[9]根据某三甲医院的实际调研数据,建立了MRI检查预约仿真模型。Geng等[19]对MRI预约调度建立了马尔可夫决策过程模型。但都没有考虑MRI设备的转换成本。Qiu等[3]考虑了MRI设备在不同类型患者间的转换成本,在一个工作日内优化患者的检查次序和检查时间。但没有考虑跨工作日的预约排程,而现实中患者很少能在预约当天进行MRI检查[2]。其他与MRI设备调度相关的文献则通过仿真方法对调度规则进行检验,没有通过数学建模的方式对问题进行分析和求解[2,20]。因此,已有的研究成果并不能被应用于MRI检查的日间预约调度问题,同时实现降低MRI设备转换成本和及时满足患者需求两个目标。

考虑到MRI检查预约给理论和实践带来的挑战,本文将研究如何对MRI检查需求进行预约调度,以最小化更换线圈产生的转换成本以及患者等待或被拒绝的成本。针对该问题,本文建立了马尔可夫决策过程模型[8,21-22],通过策略迭代算法[23]得到医院的最优排程。为了方便医院实际应用,本文提出了3种预约调度规则:单日规则、开放获取规则和短视规则。但由于转换成本的引入,即使给定调度规则,该问题仍是一个复杂的组合优化问题。因此,本文分析了各调度规则下的问题性质,设计并证明了最优解算法。除此之外,本文还依据分而治之的思想提出了忽略容量约束的分解算法[21]。通过数值实验发现,在MRI设备的检查能力紧张或患者等候成本高,即单日容量较小或等待成本较大时,最优解倾向于不开放未来工作日的预约,以避免增加等待成本,此时采用单日规则可实现最优调度。当医院希望尽快满足患者的检查需求或MRI设备转换耗时较短,即拒绝成本较高或转换成本较低时,开放获取规则与最优解的性能差距仅为1.29%。在患者等待成本较低时,可以采用短视规则算法将部分患者安排到后续工作日,从而降低MRI设备转换成本和拒绝成本,此时与最优解的性能差距为10.75%。在MRI设备的检查能力紧张或非常充足时,医院可以忽略检查能力约束,对每个类型的病人单独通过策略迭代算法进行调度,再通过本文提出的分解算法来构造符合检查能力约束的排程,此时与最优解仅有不超过1.5%的性能差距。通过使用上海某大型综合医院的实际数据进行模拟,并对比医院的实际运营情况,本文发现,使用本文设计的规则和算法,能在检查容量配置、患者拒绝比例、患者平均等待天数、日平均患者类型数等指标上取得显著改善。

本文的贡献主要有:

(1) 所建立的模型具有较强的一般性,如仅需假设需求具有马尔可夫性、转换成本和等待成本单调递增,能广泛应用于不同环境和场景。

(2) 设计了易于应用的调度规则与算法,对不同规则的应用效果及其所适用的场景进行了比较和分析,为医院MRI预约调度提供了管理洞见。

(3) 过往文献在模型建立时没有考虑MRI设备的转换成本,本文同时考虑了设备转换成本、患者等待成本和被拒绝成本,除了直接用于MRI检查场景,还可用于其他具有类似转换成本的预约调度问题,填补了预约调度文献在这方面的空白。

1 模型构建与求解

1.1 数学模型

符号及含义:

T——可预约的时间范围

J——检查类型的数量

M——医院每日检查能力上限

St=——第t期初的排程表

Dt=}——第t期的检查需求

At=}——对第t期需求的排程表

fc——转换成本函数

fw——患者等待成本函数

cr——患者拒绝成本

gt(St,Dt,At)——医院在第t期的成本

NN——医院的总经营周期

δ——折现率

π={μ1,μ2,…,μNN}——医院选择排程表的策略

SDP——单日规则(Same Day Policy)

OAP——开放获取规则(Open Access Policy)

MP——短视规则(Myopic Policy)

DA——分解算法(Decomposition Algorithm)

由于MRI设备检查不同类型患者时需要更换线圈,这会造成一定的时间损耗,从而产生转换成本。如果不能及时安排MRI检查,则又会降低患者满意度,甚至导致患者病情恶化。因此,医院需权衡转换成本与患者等待或被拒绝的成本。

本文对成本函数做出以下假设:

假设1若在同一个工作日内有n种不同的检查类型,则产生转换成本fc(n),是n的一般性单调递增函数;若一个患者从提出需求到接受检查需等待m天,则产生患者等待成本fw(m),是m的一般性单调递增函数;每拒绝一位患者产生拒绝成本cr1)医院可通过成本函数fc、fw 和参数cr 来体现对不同成本的重视程度。例如考虑线性函数fc(n)=cr n 和fw(m)=cw m,则:cw ＜cc,cr ＜cc,表示医院非常重视MRI设备使用效率,反之则表示更重视患者就医体验。

在实践中,每天能进行的检查数量受MRI设备检查能力的限制,假设每天最多进行M个检查。这里,采用每天检查数量的上限,而非每天检查总时长的上限,有以下两点原因:①在实践中,MRI检查所耗费的时间一般是固定的,因此控制检查数量,近似于控制检查总时长;②本文主要考虑转换成本与延迟检查之间的权衡,避免对检查时长进行建模,能让模型更清晰地捕获问题的实质。此外,在数值实验中,本文将问题拓展为给定每天检查总时长的上限,考虑不同类型检查耗费时间不同的情况,能得到相似的结论(见3.4节)。

给定第t期的初始预约表St、检查需求Dt和排程表At,可以计算医院在第t期产生的成本,即

式中:第1部分表示排程表At产生的患者等待和拒绝成本;第2部分表示在第t期产生的转换成本,其中,0-范数‖x‖0的取值为向量中非零元素的数量,即安排在第t期的患者类型的数量。

第t期结束后,医院根据当前预约表St和排程表At更新预约表:删除当期已经完成的预约,保留未被服务的预约,得到第t+1期开始前面临的预约表St+1。则预约表的更新过程为

假设医院考虑NN期的总成本2)当NN 充分大时,可以视为考虑无穷长时间上的总成本,即医院整个经营周期的(折现)总成本,折现率为δ,给定初始预约表S1、检查需求D1和策略π={μ1,μ2,…,μNN},其中,μt表示在第t期对每种可能的预约表St及检查需求Dt,执行怎样的排程At,即μt是预约表St及检查需求Dt的函数,则医院从第1～第NN期的总成本为

因此,医院面临的优化问题(P1)为:

其中:式(4)为正整数约束,即MRI设备的预约排程以每个检查需求为单位;式(5)为检查需求约束,即每个检查需求都需要被安排或拒绝;式(6)为MRI设备检查能力约束,即安排在同一期的检查数量之和不超过M。

优化问题(P1)求解的难度来自3个方面:①决策变量有时间和检查类型两个维度,而过往的预约调度文献只有时间一个维度;②由于安排的检查日期和患者类型都是整数变量,所以这是一个组合优化问题;③由于0-范数的引入,导致目标函数是非线性的,无法将DP问题改写为整数规划问题。

1.2 最优解求解

针对中小规模问题,可采用策略迭代算法得到最优解。策略迭代算法可以用来求解包含有限种状态和有限种控制的动态规划问题。首先选择初始策略π1,该策略规定了每种状态下执行的控制。其次计算在策略π1下每种状态的性能势(Potential),即在策略π1下每种状态的长期成本。最后进行策略改进:对每种状态,选择使执行控制产生的当前成本与执行控制后新状态的性能势之和最小控制。若改进后的策略与原策略不同,则计算新策略下每种状态的性能势,并继续进行策略改进。曹希仁[23]证明了策略迭代算法能收敛到最优策略(应用策略迭代算法求P1最优策略的伪代码见附录A)。

2 近似算法

2.1 单日规则

虽然策略迭代算法能得到最优解,但由于计算复杂度高,无法求解大规模问题,故参考医院在MRI预约调度上的管理实践,本文提出3种预约调度规则。

在实践中,许多医院为了方便管理,对每个检查需求,只能选择当天检查或拒绝,不开放未来日期的预约,本文将该排程规则记为“单日规则”。在单日规则下,第t+1期初的预约表St+1不受第t期的决策At的影响。因此,动态规划问题(P1)转换为在每期初求解整数规划问题(P2):

虽然通过Gurobi等求解器可以得到P2的最优解,但在大规模问题中依然需要较长的求解时间。因此,根据P2最优解的性质,设计了求解P2最优解的多项式时间算法,记为“单日规则算法”(SDP algorithm)。单日规则算法伪代码如下所示:

证明见附录B。

由于在单日规则下只允许当天检查或拒绝,医院一旦选择接受一个j类检查,则多接受一个j类检查不会增加转换和等待成本,只会降低拒绝成本。因此,一旦接受一个j类检查,医院应尽可能多接受j类检查,直到达到需求或容量约束。

命题2给定当前预约表St、检查需求Dt和可行排程At,若At满足

其中:nr为排程At中被拒绝的检查需求数量;c1=为排程At中第1天的剩余容量;nc为在排程At下第t期服务的检查类型数量,则增加第t期服务的检查类型数量会增加总成本。

若从拒绝全部检查需求开始,逐渐增加当期检查的检查类型,则命题2提供了这个过程的停止条件。为可能降低的拒绝成本的最大值,fc(nc+1)-fc(nc)为增加一个检查类型所产生的转换成本。若降低的拒绝成本小于增加的转换成本,则不再增加当期的检查类型。

则接受j0类检查会增加总成本。

命题3提供了增加的检查类型的条件,若

则接受j0类检查所降低的拒绝成本,无法覆盖其带来的转换成本的增加,因此不应该接受j0类检查。

定理1单日规则算法能得到P2的最优排程,计算复杂度为O(J),其中J为检查类型数量。

2.2 开放获取规则

尽管单日规则简单方便,但不开放未来工作日的预约会导致许多检查需求被拒绝,损害患者就医体验。同时,在检查需求波动很大的情况下,也会导致产能的浪费。为了尽可能减少患者被拒绝的情况和产能的浪费,本文提出“开放获取规则”,即只有在前一期安排的检查数量达到容量上限时,才开放下一期的预约,当T期全部约满时,才允许拒绝患者。由于开放获取规则要求尽可能将患者往前安排,故考虑未来成本而调整排程的空间很小,因此,在开放获取规则下忽略未来成本,得到整数规划问题(P3),即:

其中,式(10)衡量了排程At在第t期产生的等待成本、拒绝成本和转换成本。式(4)～(6)分别为正整数约束、检查需求约束和医院服务能力约束。式(8)、(9)保证了可准确衡量医院当期服务的检查类型数量,其中为充分大的正整数。式(11)～(13)为开放获取规则约束。式(12)保证当排程表的第i行有安排检查时,r i=1;式(11)保证当r i+1=1时,第i行安排的检查数量达到容量约束M。通过研究,得到P3最优解的性质:

由于开放获取规则要求只有在前一期排满时才开放下一期预约,故任一可行排程At都满足:

换言之,对给定的预约表St和需求总量当期产生的等待成本与拒绝成本是确定的,只需要选择使转换成本最小的排程。

命题5给定当前预约表St和检查需求Dt,将所有满足的检查类型记为集合JJ1,则存在最优排程At满足

若在当前预约表St中,已经安排了j类检查在当期进行检查,则在当期安排更多j类检查不会增加转换成本,因此,医院的最优选择是优先安排在集合JJ1中的检查类型,直到达到容量或需求约束。安排满当期检查后,将剩余检查安排到后续工作日不会在当期产生转换成本,根据命题4,所有符合开放获取规则的排程都产生相同的等待成本与拒绝成本。若集合JJ1中的检查需求无法填满当期容量,类似命题4,本文将不在集合JJ1中的检查需求按照从大到小的顺序安排在当期,直到达到容量或需求约束。根据命题4与命题5,设计了求P3最优解的多项式时间算法。

定理2开放获取规则算法(OAP algorithm)能得到P3的最优解,计算复杂度为O(TJ)。开放获取规则算法伪代码如下所示:

开放获取规则算法

2.3 短视规则

虽然开放获取规则能避免医院产能浪费,但会增加医院成本。如当天剩余1个检查名额,但有10个j类检查尚未分配时,按照开放获取规则,医院要在当天进行其中1个j类检查,再将剩余9个检查安排在下一期,产生两次转换成本。显然,当患者等待1天的成本小于转换成本时,将10个检查都安排在下一期更好。为了避免过度增加转换成本,考虑短视规则(Myopic Policy),即忽略未来成本,在每期初最小化等待成本、拒绝成本与转换成本之和,将P1转换为整数规划问题(P4),即:

P4与开放获取规则下的问题(P3)基本相同,只是删除了确保“只有在前一期安排的检查数量达到容量上限时,才开放下一期的预约”的约束式(11)～(13)。同样,本文也通过探究P4最优解的性质来设计多项式时间的求解算法。

由于安排在第2～T+1行的检查不在当期产生转换成本,故最优选择是尽量把检查往前安排。可以预见,短视规则应该在检查需求不超过检查容量太多的情况下使用,否则与开放获取规则的差异不大,但在检查需求不太大时,短视规则可以通过转移部分需求到下一期来降低转换成本。基于命题6,寻找P4 最优解等价于找到排程表第1 行的最优解。

命题7与命题5相同,增加已被安排在当期的检查类型不会增加转换成本。在开放获取规则下,若集合JJ1中的检查没有填满排程表的第1行,需继续填入其余类型的患者,直到达到容量上限。但在短视规则下,需要通过比较接受多一类检查增加的转化成本与降低的等待成本来决定。

命题8与命题4类似,说明了应优先接受需求量更大的检查类型。由于,故只有当接受j类检查降低的等待成本超过增加的转换成本时才选择接受,而检查需求量大的检查类型有更大的机会实现该条件。

定理3短视规则算法(MP algorithm)能得到P4的最优解,计算复杂度为O(TJ)。短视规则算法伪代码如下所示:

短视规则算法

2.4 分解算法

在单日规则、开放获取规则和短视规则下,医院能快速为新抵达的需求安排检查时间,却没有考虑当期排程对未来成本的影响。而考虑未来成本的策略迭代算法在求P1最优解时,控制的维度是时间×类型,算法复杂度非常高。根据分而治之思想,将原问题按照检查类型分解为J个子问题,每个子问题的控制只有时间维度,算法复杂度大大降低。据此,本文设计了忽略容量约束的分解算法(Decomposition Algorithm),可在考虑未来成本的情况下近似求解P1。其每个子问题(P5-j)为:

衡量了j类检查在第t期的等待成本、拒绝成本与转换成本。式(15a)～(15c)分别为对j类检查的整数约束、需求约束和容量约束。若M=+∞且f(n1)+f(n2)=f(n1+n2),则求解J个子问题(P5-j)等价于求解原问题(P1)。若M＜+∞,则J个子问题的最优解不一定能组合为原问题的可行解。在分解算法中,优先接受检查数量大的类型,将检查数量少的检查类型往后推,能在降低转换成本的同时,把J个子问题的最优解转换为原问题(P1)的可行近似解。分解算法伪代码如下所示:

分解算法

3 数值实验及案例分析

为检验上述4种算法的效果,本文设计了两组数值实验,分别比较了小规模问题中4种算法与最优解的性能差距以及大规模问题中各算法在不同参数条件下的表现。最后,通过医院实际数据分析比较各算法的效果。

3.1 小规模数值实验

为了控制问题规模,使最优解可以通过策略迭代算法得到,设置预约时间范围T=2,即只能将患者安排在当期、下一期或拒绝;检查类型数量J=2;检查需求服从均值为λ=1的泊松分布,且限制最大值为2。在这种问题规模下,最大需求为8人,因此将检查容量按1～8均匀取值,即M∈{1,2,…,8}。方便起见,成本使用线性函数,即:fw(t)=cwt,fc(n)=ccn。将cw(1位患者等待1天的成本)的均值标准化为1;拒绝1位患者的成本应大于让1位患者等待多日,因此将cr的均值设为6;将转换成本cc的均值设为3,使其略大于将一类患者推迟一天产生的等待成本。在实验中,cw、cr和cc根据其均值按均匀分布取值,即:cw∈{0,0.5,…,2},cr∈{2,4,…,10},cc∈{0,1,…,6}。

基于上述参数设置,根据策略迭代算法、单日规则算法、开放获取规则算法、短视规则算法和分解算法求解最优策略π,并使用值迭代计算各参数组合下的长期平均成本,所得结果如表1 与图1 所示。其中,性能差距为各算法下长期平均成本超出最优解的百分比,即

图1 小规模数值实验结果Fig.1 Results from small-scale numerical experiment

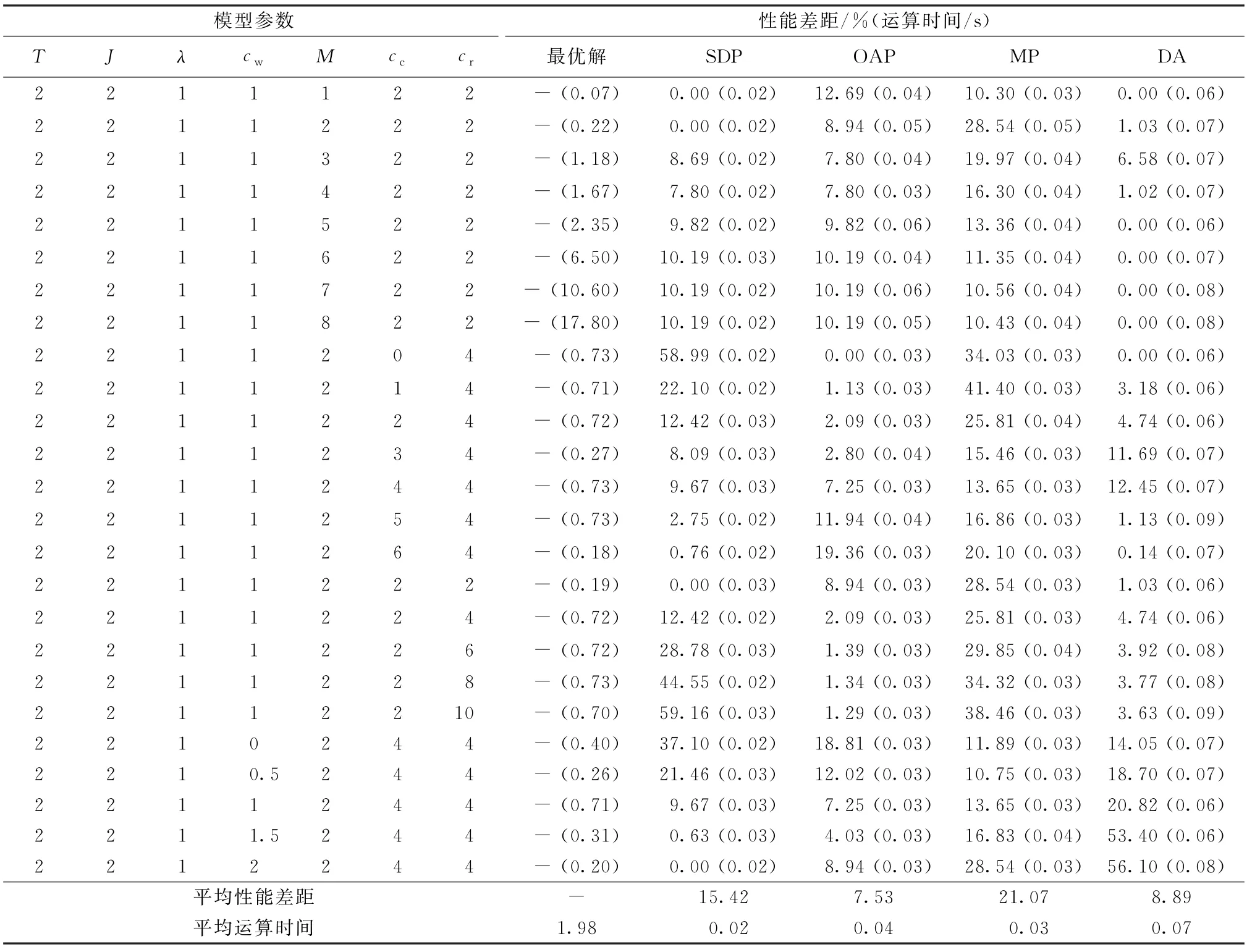
表1 小规模数值实验结果Tab.1 Results from small-scale numerical experiment

由表1可以看出,每种近似算法的计算时间都远低于策略迭代算法。随着MRI检查单日容量M的增加,策略迭代算法的运算时间从0.07 s快速上涨到17.8 s,而其他近似算法的运算时间始终不超过0.1 s。换言之,与策略迭代算法相比,本文提出的近似算法不存在维数灾难问题。由表1和图1可以看出,每个近似算法适用的情形不同,且在每种参数组合下,都存在至少一种表现优异的算法。

在医院检查能力紧张时,单日规则算法与分解算法表现最佳,长期平均成本达到了最优。这是因为在医院检查能力紧张时,几乎每天新抵达的检查需求都超出检查能力限制,所以最佳选择是不开放未来预约,在每期达到容量限制后拒绝剩余需求,这与单日规则一致。同时,在检查需求大大超出检查能力时,通常存在只需挑选一个类型的检查,其需求就能填满当天的检查容量,因此将原问题按照检查类型分解为J个子问题不影响最优解。

随着医院检查能力的提高,会出现需求时而大于容量、时而小于容量的情况,因此,最佳选择是将当期抵达的需求安排到未来工作日,以抚平需求波动,这与单日规则存在较大差异,因此,其性能差距增大。同样,在医院检查能力提高时,分解算法由于没有考虑不同类型检查间的相互影响,导致其性能差距增大,但其表现依然优于其他算法,性能差距小于6.6%。当医院检查能力充分大时,排程不受检查能力的限制,且由于数值实验考虑的是等待成本与转换成本线性增加,所以分解算法能得到最优排程。

在拒绝成本较低时,最优排程倾向于拒绝患者而非让其等待并增加下一期的转换成本,这与单日规则相似,此时单日规则的表现最好。当拒绝成本变大时,最优排程倾向于不拒绝患者,这与开放获取规则类似,故开放获取规则的表现最好。

在MRI设备转换成本较低时,最优排程更有可能通过增加检查类型来降低患者等待和拒绝成本,这与开放获取规则类似,因此,其表现最佳。在转换成本较高且某类检查数量较多时,才为该类检查花费转换成本。在单日规则中,只有在接受某类检查所降低的拒绝成本超过其增加的转换成本时,才接受该类检查,而降低的拒绝成本随检查数量递增,因此,单日规则在此情形下表现良好。在分解算法中,求解每个子问题时,都权衡了该类检查带来的拒绝成本和转换成本,因此,分解算法在此情形下也表现良好。

在等待成本较低时,由于短视规则受等待成本的影响较小,且比单日规则能通过让患者等待来降低拒绝成本、比开放获取规则能考虑到转换成本的影响、比分解算法能考虑到不同类型检查间的相互作用,故性能表现最好。在等待成本适中时,由于等待成本增加,短视规则比前一种情形更难通过让患者等待来降低拒绝和转换,并由于等待成本不够高,故让患者等待而非直接拒绝的开放获取规则表现最佳。在等待成本较高时,最优排程倾向于不让患者等待,与单日规则较为相似,因此,其表现最佳。

通过小规模问题的数值实验可以看出,在不同参数情况下,都能找到效果较好的近似解,因此,医院可以根据MRI检查能力的紧张与否,拒绝成本、等待成本及转换成本的高低来选择合适的算法为患者预约检查日期。尽管单日规则算法和短视规则算法在某些情况表现极佳,但从平均性能差距来看,它们的总体表现劣于开放获取规则算法和分解算法,因此,医院在采用单日规则和短视规则时需要仔细辨别适用的场景。

3.2 大规模数值实验

通过小规模问题证明了近似算法的有效性,本文对更方便应用的单日规则、开放获取规则和短视规则进行规模较大的数值实验,以探究3种规则在大规模情形下的表现。

大规模数值实验的参数设置如下:一般医院可预约时间范围为一周,即T=7;在实践中,一般会用到7种MRI线圈,即J=7;上海某三甲医院日均MRI检查需求约为100,故假设每类检查需求服从均值λ=15的泊松分布;每日检查能力设为M∈{85,105,125},分别对应检查能力紧张、均衡和充分的情况;患者单位等待成本的均值标准化为1,故设cw∈{0.5,1,1.5};将拒绝成本设为等待成本的10倍(略大于将患者安排在最后一天的等待成本),故设cr∈{5,10,15};转换成本应略大于将某类需求全部推迟一天的等待成本,故设cc={10,20,30}。基于上述参数,使用Matlab进行仿真求解,部分结果如图2所示(详细结果见附表B1)。

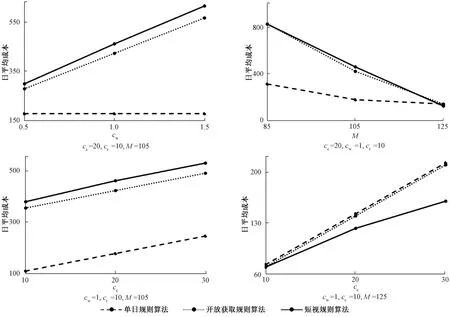
图2 大规模数值实验结果Fig.2 Results from large-scale numerical experiment

由此可见,单日规则的效果几乎不受患者等待成本的影响,但开放获取规则和短视规则下的日平均成本随等待成本的增加而显著增加,并且等待成本越大,3种规则的表现效果差异越大。此外,随着医院检查能力的增加,所有近似算法的日平均成本都会下降。在医院检查能力紧张和均衡时,单日规则表现最佳。在医院检查能力充足时,短视规则表现更好,三者差异不大,但随着转换成本的增加,3种规则的性能差异越发明显。这说明,转换成本对系统性能的影响非常显著。在转换成本较大时,即使医院检查能力充足,3种规则的性能差异也十分明显。总之,在患者等待成本越大、医院检查能力紧张、转换成本较大时,医院需要仔细选择所使用的预约规则。

3.3 医院实际案例分析

为了验证现实中近似算法的效果,本文搜集并整理了上海某大型综合医院198 天共21 585 次MRI检查的申请日期、检查日期及检查类型的数据,对单日规则算法、开放获取规则算法和短视规则算法的效果进行评价。

医院案例数据中,患者检查需求可按使用线圈的不同分为7种类型,而日均检查类型为5.82种,检查类型最少时为1种,可以看出,医院在有意控制每天检查类型的数量,但效果不佳。从每日产生的检查需求来看,均数为108.43次,方差为3 119;从每日实际检查数量来看,均值为100.36次,最大值为241次,方差为3 310。这说明,MRI的预约调度并没有起到平滑需求波动的效果,每天的检查工作量极不平衡,同时存在着设备的闲置和加班。从患者的就医体验来看,平均每个患者等待2.40天,最长等待时间为27天,并且还有7.47%的检查需求被拒绝,就医体验不佳。

在案例分析中,将可预约的时间范围设为一周,即T=7;根据MRI线圈类型,将J设为7;将实际数据中每日检查数量的中位数设为检查容量,即M=118;将每位患者等待1天的成本标准化为1,即cw=1;拒绝1名患者的成本应稍大于将患者安排到最后一天,故设cr=10;转换成本应稍大于将某类需求全部推后一天产生的等待成本,故设cc=20。根据单日规则算法、开放获取规则算法和短视规则算法,对实际历史数据中的检查需求求解预约调度,并计算各个算法下拒绝率、平均等待天数、日平均检查类型数、日平均检查量、日检查量的方差等指标,并与医院实际情况进行对比(见表2)。

表2 实际案例分析结果Tab.2 Analysis from real case

开放获取规则和短视规则在每项指标上都优于医院实际情况,在降低医院成本的同时提高了患者就医体验。单日规则通过减少日平均患者类型数降低了医院成本,但提高了患者拒绝率,可能会损害患者的就医体验,更适合在检查需求远超于检查能力的医院中使用。

3.4 拓展模型数值实验

前文使用“每天最多检查的患者数量”来衡量医院MRI设备的检查能力,但实践中可能出现不同类型检查耗费的时间不同的情况,而相同的设备可能每天能进行10个I类检查,但只能进行5个II类检查。因此,通过简单的数值实验说明使用“每天最多检查的患者数量”或“MRI设备总运行时间”来衡量医院检查能力并不会显著影响本文的主要结论。

参考小规模数值实验中的参数设置,进一步区分两类检查耗费的时间:假设II类检查的耗费时间为1个单位时间,I类与II类检查的耗费时间之比为{0.7,0.8,…,2},最后得到图3所示结果。

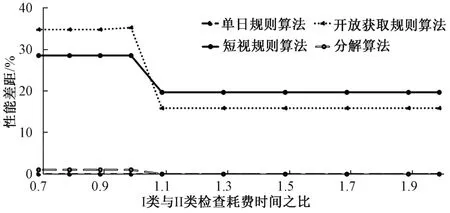
图3 拓展模型数值实验结果Fig.3 Results from extended numerical model

由图3可以发现,3种算法的性能差距都在检查时间之比为1时发生跳转,在其他情况下保持稳定。这是由于本文设置了检查总时间M=2,即每天MRI设备最多运转2个单位时间,在检查时间之比小于1时,相当于检查容量M=2;在检查时间之比大于1时,相当于检查容量M=1,所以性能差距发生改变。可见,本文所提出近似算法的表现与检查容量有关,而与检查时间之比几乎无关。

4 结论

本文考虑了医院核磁共振检查(MRI)在扫描患者不同部位时产生的转换成本,以及未能及时满足患者就医需求而产生的等候及拒绝成本,对MRI设备的预约调度问题建立了马尔可夫决策过程模型,以最小化医院长期总成本,并通过策略迭代算法得到最优排程。为了降低计算复杂度,本文考虑了单日规则、开放获取规则和短视规则,但由于转换成本的引入,即使在给定调度规则下,该问题仍是一个组合优化问题。因此,本文分析了各调度规则下的问题性质,设计并证明了各求解规则下最优解的多项式时间算法。在单日规则、开放获取规则和短视规则下,最优解算法的计算时间与患者总量无关,只随患者类型数量J和预约时间范围T线性增长,大大降低了计算复杂度。本文还依据分而治之的思想设计了分解算法,得到原问题的近似解。从数值模拟结果来看,本文提出的方法均能有效近似最优解。从上海某大型综合医院的实际案例可以看出,本文设计的近似算法在检查容量配置、患者拒绝率、平均等待天数、日平均检查类型数等指标上取得显著改善。

本文提出的算法对医院MRI设备预约调度具有实践指导意义。

一方面,本文提出的多项式时间算法计算复杂度低,能快速得到对应调度规则下的最优排程;另一方面,本文只要求成本函数递增,没有对设备转换成本和等待成本之间的关系做出假设。因此,医院可以根据实际情况灵活选择适合的调度规则及算法。

当MRI设备检查能力紧张时,应采用单日规则,因为无法通过开放后续工作日预约来抚平需求波动,反而会增加转换成本与患者等待成本。当医院不希望拒绝患者的检查需求或MRI设备转换成本低时,可以采用开放获取规则,充分利用MRI设备的检查能力。当MRI设备检查能力充足且患者检查类型多、可预约时间范围长时,应采用短视规则,通过将部分检查需求移动到后续工作日来降低MRI设备的转换成本,从而降低总成本。当MRI设备的检查能力非常紧张或非常充足时,医院可以忽略检查能力约束,采用分而治之的方法,对每个类型单独通过策略迭代算法进行排程,再组合为可行的排程表,此时与最优解仅有不超过1.5%的性能差距。

从直觉上看,MRI设备的检查能力越紧张,容量约束的影响越大。但在MRI设备的预约排程问题中,为了降低患者等待和拒绝成本,医院应尽量将患者排在靠前的日期,而为了降低转换成本,在每期应尽量先处理完一个类型的检查后再考虑下一个类型的检查,这与分解算法的思想是类似的,可以很好地近似最优解。当MRI设备的检查能力非常充足时,容量约束冗余,因此,分解算法也表现良好。

虽然本文研究的是MRI设备的预约排程问题,但提出的模型、算法和管理内涵同样能应用于存在转换成本的其他预约排程问题。例如,在场地出租企业中,若前后预约场地的顾客都用于开会,则无需重新布置场地;若前一位顾客预约场地用于开会,而后一位顾客预约场地用于演出,则产生了场地布置成本。

本文的研究有许多可拓展方向。例如考虑MRI设备的检查能力存在硬性约束,规定了每天患者检查数量的上限,未来研究可以考虑软检查能力约束,允许超出MRI设备检查能力,但产生超时工作成本。另外,本文假设不同检查需求的患者的等待成本函数一致,但在现实中,特定类型患者的就医需求可能更为迫切。本文的模型、排程规则及算法可以作为未来更多相关问题的研究工具。

附录A

策略迭代算法假设每个工作日的患者检查需求Dt相互独立,且所有可能的检查需求Dt包含于有限集合DD,即Dt∈DD。假设第t期检查需求为Dt的概率为P(Dt),且由于预约表St需满足正整数约束与医院服务能力约束,故存在有限集合SS包含所有可能的预约表St。同理,由于排程At需满足正整数约束、检查需求约束和医院服务能力约束,故给定St∈SS,Dt∈DD,存在有限集合AA(St,Dt)包含所有满足约束式(4)～(6)的排程At。通过如下所示伪代码,求解优化问题(P1)的最优策略。

策略迭代算法

附录B

大规模数值实验详细结果见附表B1。

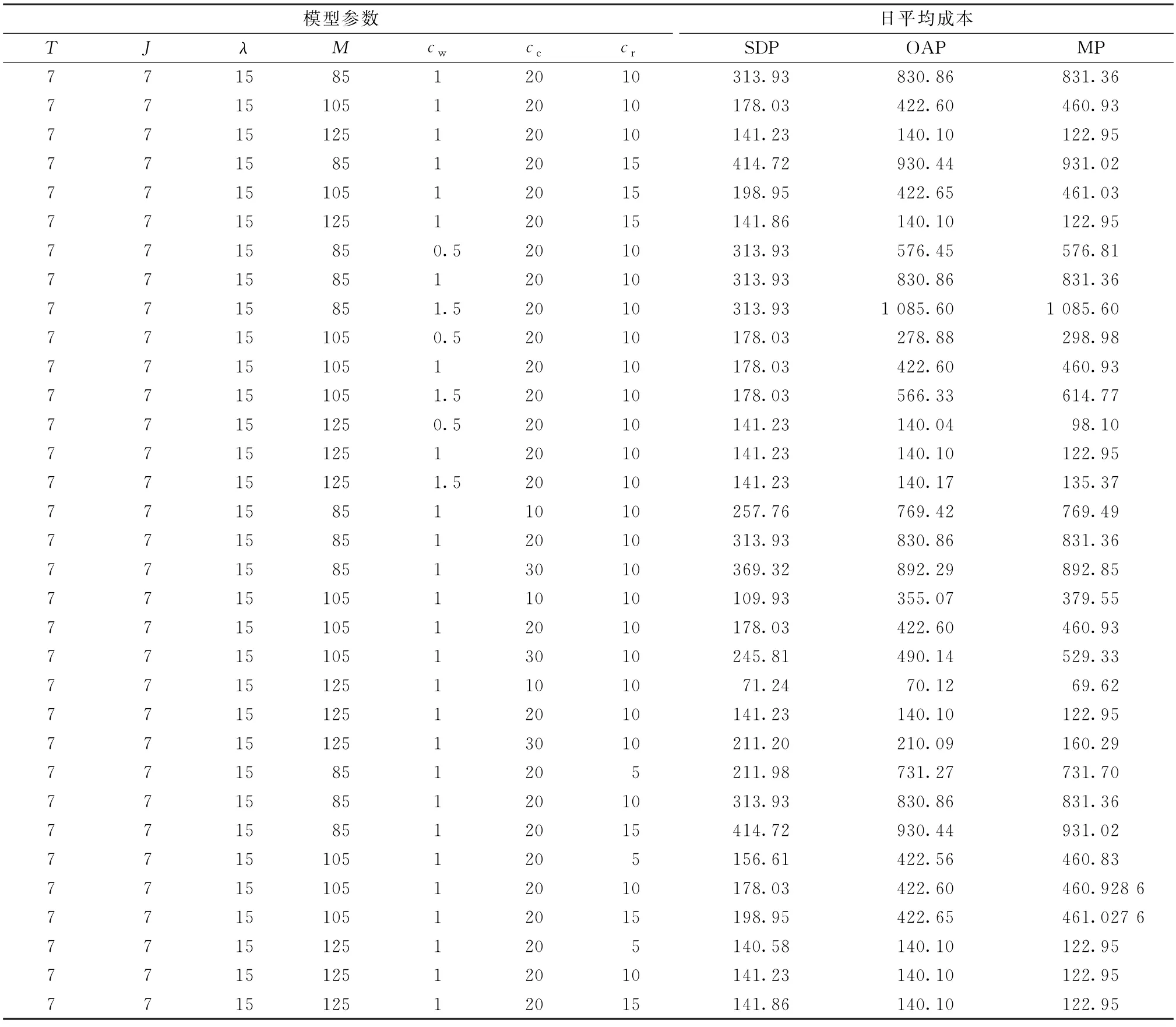
附表B1 大规模数值实验结果Tab.B1 Results from large-scale numerical experiment

附录C

因此,当期需求总量相同的排程At1和At2安排在每期的检查/拒绝总数相同,则

命题8的证明同命题6的证明。

命题9的证明同命题4的证明。

综上可知,无法通过修改排程At得到成本更低的可行排程,因此,At是最优排程。