车辆荷载对公路隧道结构及围岩动力响应研究★

张志强，王小敏

(1.山西省交通规划勘察设计院有限公司,山西 太原 030032; 2.山西能源学院,山西 晋中 030600)

0 引言

21世纪以来,我国水下隧道广泛建设,2001年—2010年建设了77条水下隧道,2011年—2020年建设了154条水下隧道,主要穿越长江、黄浦江、钱塘江,其中地铁、公路隧道居多[1]。近20年,随着大量的过江隧道投入运营,众多学者持续关注结构稳定、环境影响和安全性等方面的问题。车辆荷载会对隧道结构产生冲击振动,在车辆荷载的长期作用下,容易导致路基破坏,路基中应力集中分布有可能引起隧道结构破坏。因此水下盾构隧道动力响应关乎安全的问题,有重要的研究意义。

目前国内外学者已针对此问题进行了一系列研究。刘卫丰等[2]采用有限元法模拟隧道结构,采用边界元法模拟隧道周围土体自由场,通过建立三维周期性有限元-边界元耦合的数值模型,对地铁列车运行引起的隧道及自由场动力响应进行预测。高盟等[3]研究了饱和半空间中地下衬砌结构在突加均布荷载作用下的瞬态响应解答,并分析了隧道结构埋深对衬砌土体交界面处动应力分布的影响。王建炜等[4]通过建立三维动力有限元模型,对公路和轨道交通载荷单独作用及共同作用时的隧道动力响应进行了分析,获得了公铁两用隧道的动力响应规律。刘雪珠等[5]研究了埋置无限长圆形隧道内一系列等距移动点荷载作用下饱和土体中的动力响应,并通过数值模拟,分析了系统的临界速度及系列等距移动荷载作用下的共振与消振现象。

上述文献中作用在隧道上的荷载从均布荷载发展到移动荷载,但主要以列车荷载为主。目前隧道动力响应研究的主要对象是铁路及地铁隧道,国内外针对车辆随机荷载作用下的公路隧道振动响应研究较少。

本文以南京应天大街隧道软土地层段为工程实例,将Simulink仿真计算出车辆随机动荷载加载于隧道模型上,从行车数量角度分析越江公路隧道在车辆随机动荷载作用下产生的振动在路面板和隧道围岩土体中传播与衰减特性。

1 车辆随机动荷载计算

1.1 车辆随机动荷载模型

道路表面相对于理想平面的偏离指的是路面不平度,用来描述路面的起伏程度。在路面不平度的激励下,行驶的汽车会对路面产生随机的动荷载[6]。

在道路工程中,路面不平度的统计特性用功率谱密度函数来表示:

(1)

其中,Gd(n)为路面不平度功率谱密度;n为空间频率,m-1;n0为参考空间频率,n0=0.1 m-1;Gd(n0)为参考空间频率n0下的路面功率谱密度,即路面不平度系数,m2/m-1;W为频率指数,决定路面功率谱密度的频率结构。

已知在空间频率n的路面上当车辆以恒定速度v行驶时,时间频率f=vn,可将空间功率谱转换为时间功率谱:

(2)

本文采用基于滤波的白噪声激励模拟作为路面不平度的时域数值模拟方法。由式(1),式(2)可得时间频率下的路面功率谱密度(频率指数W取2):

(3)

考虑路面功率谱在低频范围内近似水平的情况,在路面高程时域模型中引入下截止频率f1,则滤波白噪声表达的路面功率谱密度Gd(f)为:

(4)

其中,f1为下截止时间频率,Hz;p(f)为传递函数;σ2为随机白噪声W(t)的方差,值取1。

引入角频率ω表示,其中ω=2πf,同时频率响应函数经过傅里叶及拉普拉斯变换,可得路面高程时域表达式:

(5)

本文采用自由度的1/4车辆模型用以模拟计算车辆动荷载,如图1所示。

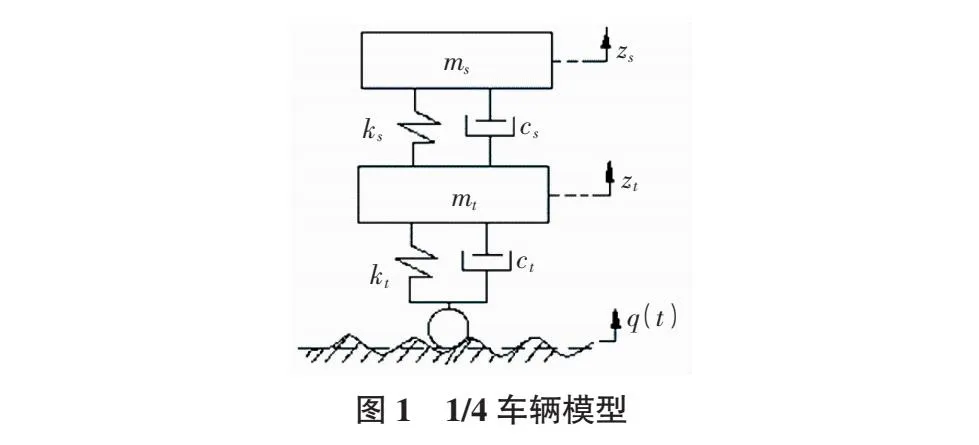
根据牛顿第二定律可得图1模型动力方程:

(6)

其中,ms,mt分别为悬挂和非悬挂部分质量;ks为悬挂刚度系数;kt为轮胎刚度系数;cs为悬挂缓冲阻尼系数;ct为轮胎阻尼常数;zs,zt分别为悬挂部分质量、非悬挂部分质量垂向振动位移;q(t)为路面高程时域模型激励。

由上述分析确定了路面不平度激励模型和1/4车辆模型,联立式(5),式(6)可得轮胎对地面的附加动荷载为:

(7)

作用于路面的车辆随机动荷载包含车辆静荷载和附加随机动荷载:

Ft=G+Fd

(8)

其中,Ft为随机动荷载;G为车辆静荷载,G=(ms+mt)g,g为重力加速度;Fd为轮胎对地面的附加动荷载。

1.2 车辆随机动荷载求解

采用MATLAB/Simulink软件编制随机动荷载计算程序,根据上述路面不平度激励模型和1/4车辆模型,仿真计算求出车辆随机动荷载。通过设置包括车辆、车速、路面等级等不同参数来实现随机动荷载的模拟。

车辆随机动荷载仿真计算时要保证车辆行驶长度相同,则仿真时间t需要根据车速v进行调整。采样时间ts(Sample time)初设定值为0.001 s。

隧道车辆荷载按照城-A级标准,此外调取隧道监控录像,对三车道路面板上通过的车型进行统计[7],隧道中有重型车辆通过,从最不利因素考虑,车辆随机动荷载计算时选用的重型汽车进行分析,车辆参数如表1所示。

表1 车型及参数表

通过设置MATLAB/Simulink程序中相应参数及其取值来求解路面不平度激励时双自由度1/4车辆模型的振动响应,最终得到不同车型作用于路面各点的随机动荷载。

2 隧道有限元模型

2.1 工程背景

南京应天大街长江隧道地处地形较为开阔且平坦的长江河床及高河漫滩地区。勘察揭露地层上部均为第四系松散沉积物,工程范围内的表地层为第四系全新统冲积层,岩性以粉质黏土、淤泥质粉质黏土、粉细砂为主,下伏白垩系基岩。场地地下水水位埋深为0.4 m～1.4 m,平均0.7 m,局部因地势埋深偏大,江中段隧道的最大水压可达0.65 MPa左右。

江中段盾构隧道长度约为3 020 m,圆形隧道外径为14.57 m,行车道宽度为2×3.5 m(小型车)+3.75 m(大型车),行车道限界高4.5 m,路缘带宽度0.5 m(左、右侧同),侧向净宽0.25 m,设计车速为80 km/h,车辆荷载按照城-A级标准计算。

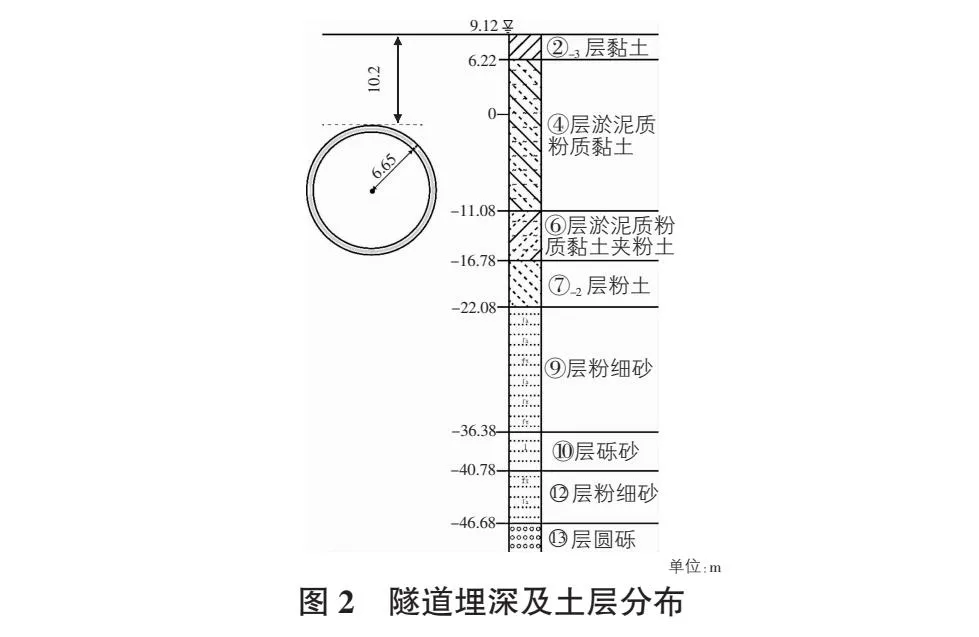
本文主要选取南京应天大街长江隧道软土层典型断面K3+700为研究对象。隧道埋深、各土层的分布及土层物理力学参数如图2所示。

2.2 模型参数及边界条件

根据工程资料,设置模型中隧道结构外径14.57 m,管片厚度为0.6 m。路面板宽度为3.75 m×3,厚度为0.6 m,箱涵侧壁高度为3.7 m,厚度为0.25 m,路面板和箱涵简化后固定在隧道结构上。隧道管片选取线弹性本构模型,侧壁管片采用C60混凝土浇筑,隧道内部结构、箱涵、路面板材料采用C40混凝土。隧道结构材料参数取值如表2所示。

表2 隧道结构材料参数

隧道ANSYS有限元模型中简化土层水平成层土,振动响应分析中非线性性质将被忽略,选择线弹性本构模型作为土体动力本构模型。由于断面K3+700土层处于长江汛期水位之下,并且在短时振动响应分析中不考虑排水作用,因此土的泊松比按照饱和土体取0.45。土层的物理力学参数见表3。

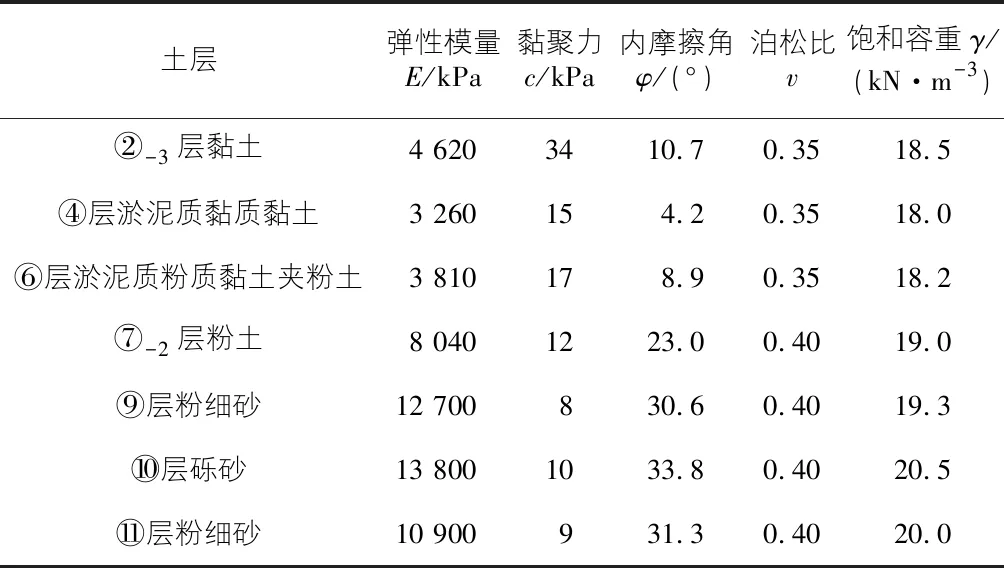
表3 土体材料参数

根据蒋英礼等[8]的研究,土体瑞利阻尼参数取值为α=0.030,β=0.002。隧道管片混凝土结构比例阻尼系数ε取常用值0.05,因此隧道结构瑞利阻尼参数的取值为α=0.085,β=0.004 5。

采用ANSYS中三维实体Solid185单元模拟隧道结构与周围的岩土层。模型中接触面的设置,将隧道结构定义为目标面,周围土层定义为接触面。行驶中的车辆距离较远处无振动影响,因此在垂直于隧道延伸方向的边界两侧设置X和Z方向约束。下部土体为黏弹性地基,采用三维弹簧元进行约束设置。模型前后设置Z方向约束。

根据上述参数及边界条件建立左线隧道三维有限元模型如图3所示,隧道延伸方向长度为150 m,宽度100 m,高度为55 m。

3 模型验证

3.1 测试方案

已有学者对车辆动力荷载作用下隧道内多测点的振动加速度进行了现场测试,隧道内各测点的布设如图4所示。

3.2 测试结果

选取快车道以下管片内侧的C测点加速度进行对比。将一辆车驶过快车道路面板时的实测激励荷载,施加在ANSYS隧道模型的快车道上,将模型中C测点的加速度时程曲线与实测加速度曲线进行对比,结果如图5所示。

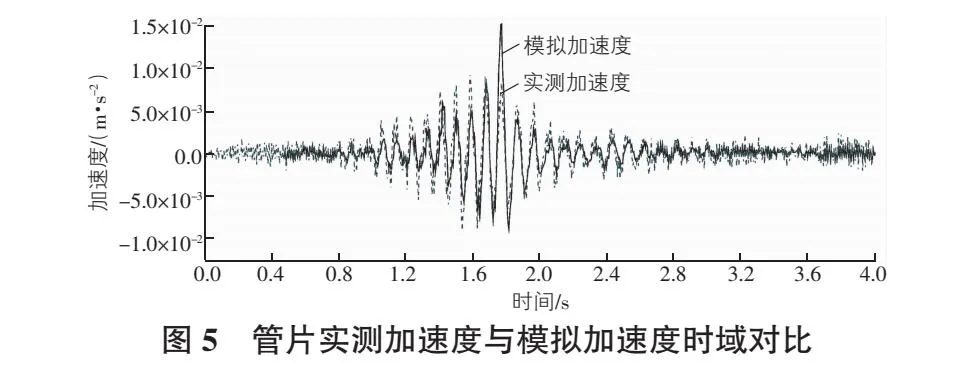
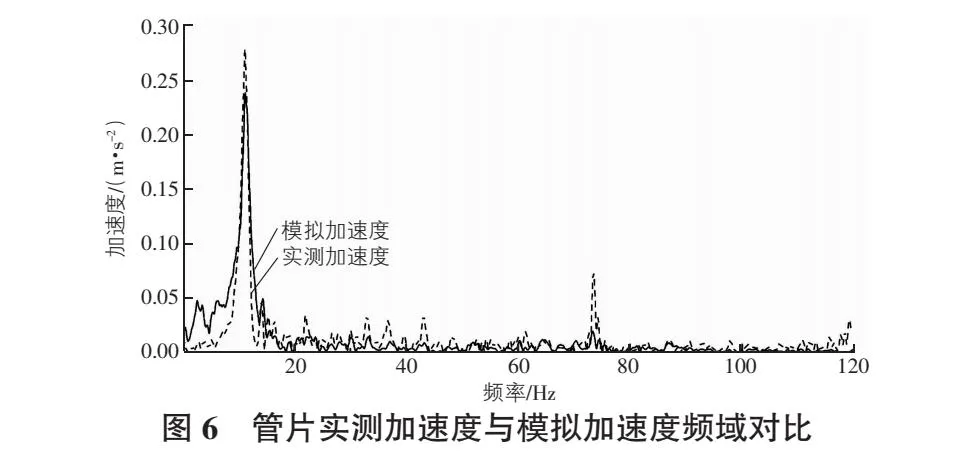
图5中,模拟获得的加速度曲线的整体振动趋势和加速度峰值变化与实测加速度基本保持一致。经过傅里叶变换得到其频域曲线,如图6所示。对比分析可得,模拟加速度在低频部分的峰值与趋势均与实测频域有很好的一致性。证明文中参数选取及隧道有限元模型的准确性。

4 单辆车隧道围岩动力响应分析

南京应天大街隧道设计车速为80 km/h,因此仿真计算中设置车速为80 km/h。车辆荷载仿真计算中路面等级设置为B。ANSYS隧道模型中,路面板长度为150 m,因此车辆行驶时间为6.75 s。单辆车荷载工况设置如表4所示。

表4 单辆车荷载工况设置

ANSYS模型中选取路面板应力响应最大的节点所在截面,分析隧道周围的土体节点应力响应。

4.1 隧道底部土层振动响应

图7为隧道底部不同深度土层的应力时程曲线。由图7分析可得,隧道底部土层承受的是竖向压应力,土层深度越深,出现的振动应力响应时间越滞后,幅值越小。最靠近隧道结构底部的粉土层应力响应最大值为115 Pa。粉土层之下的振动响应幅值非常微弱,最远处粉细砂层应力响应幅值仅为4.3 Pa。

4.2 隧道侧边土层振动响应

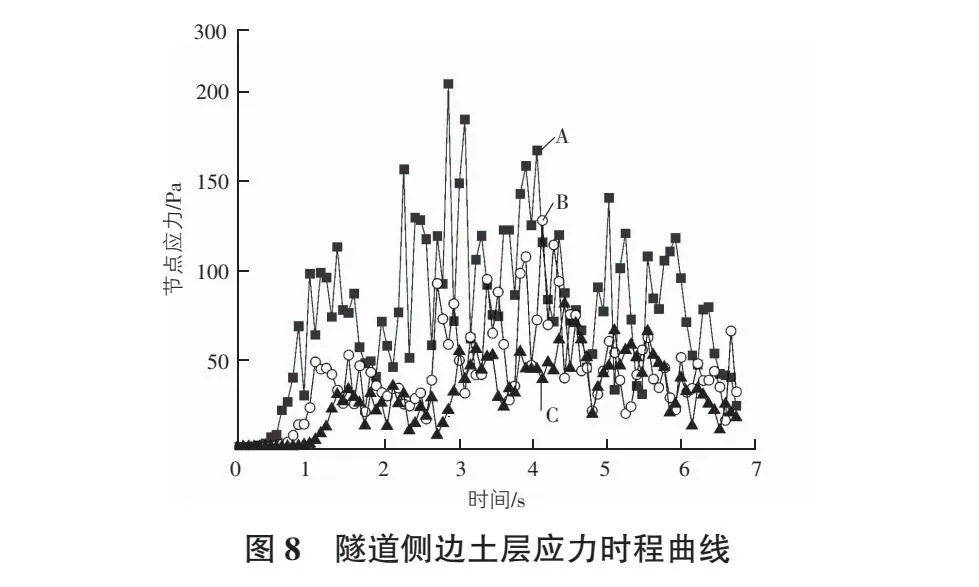
模型中,隧道路面同一水平面上,选取其与隧道中心线距离分别为10.88 m,19.78 m,26.45 m的A,B,C三个监测点。绘制三个监测点应力时程曲线,如图8所示。车辆作用于车道路面板的荷载会引起隧道侧边土层的振动响应。与路面板距离越远,最大应力响应出现的时刻越滞后、幅值越小。与路面板中心线最近的A点应力响应最大值为214 Pa,C点最大应力响应幅值仅为74 Pa。

4.3 隧道顶部土层振动响应

模型中,隧道顶部中心线上,选取不同土层中三个节点D,E,F作为监测点。三点与隧道顶部管片距离分别为2.01 m,4.49 m,7.30 m。图9为D,E,F的应力时程曲线。图中曲线显示,顶部土层的应力响应峰值较小,并且随着与顶部管片的距离增大,应力响应幅值减小,响应峰值出现的时间越滞后。距离管片7.30 m 处的F点最大应力响应幅值仅为29 Pa。

对比分析隧道底部、侧边、顶部土层的振动响应。距离隧道管片底部2 m处的最大振动应力响应幅值为115 Pa,距离隧道侧壁管片10.88 m处最大应力响应幅值为204 Pa,距离隧道顶部管片2.01 m处的最大应力响应值为66.6 Pa。对比可得:隧道同一截面处,在车辆随机荷载的激励下,隧道侧边土层的振动响应最强,顶部土层的响应最弱。

5 三辆车工况下隧道动力响应分析

南京应天大街隧道在早晚车流量高峰时段,3车道均有车辆行驶,因此,模型中设置三车道同时施加车辆随机动荷载,工况车型及车速设置如表5所示。

表5 三辆车荷载工况设置

5.1 隧道底部土层应力响应对比分析

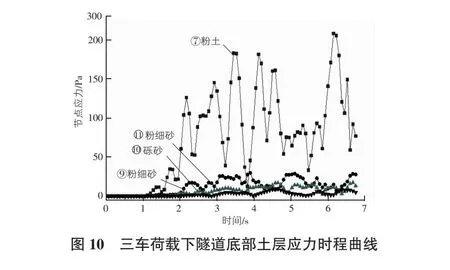
三车道同时作用车辆随机荷载的工况下,应力传递及反弹更加复杂,隧道周围土层的响应因此而更加复杂。图10为三车道车辆随机荷载均施加的情况下,隧道底部土层的节点应力响应时程曲线。由图10中分析得,紧挨隧道结构底部的粉土层中出现多个应力响应峰值,这是由于车辆荷载数量的增加,导致隧道土层中应力传递和反弹更加强烈,因此,反弹后的应力叠加产生多个应力响应峰值。距离隧道底部结构较远的土层,即使在三辆车荷载的作用下,振动响应依然微弱。

5.2 隧道侧边土层应力响应对比分析

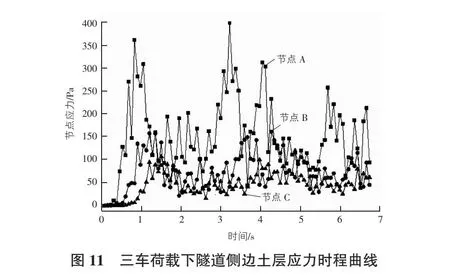
由上节分析可知,中车道路面板施加荷载时,隧道侧边土层的振动响应最大。因此,模型中选取与工况① 相同的节点A,B,C,分析三辆车随机动荷载作用下,与路面板相同深度处,隧道侧边土层的应力响应的变化情况,如图11所示。

6 结论

本文以南京长江隧道的典型截面为例,考虑不同车辆随机动荷载加载在路面板时的典型工况,采用有限元法分析了软土地层越江公路隧道车载动力响应规律,得到以下结论:

1)行驶中车辆的随机动荷载模拟受多个参数共同影响,包括车型、路面等级与车辆行驶速度等。对三个影响因素进行参数敏感性分析,得出其敏感性由大到小依次为:路面等级>车型>车速。

2)车速对隧道周围土体的动力响应影响明显,同一监测点在车速80 km/h工况下的应力响应峰值是60 km/h时的5倍。在距离隧道中心一定范围内,车辆行驶速度越快,引起的振动越强烈,但振动衰减也越快。在离隧道中心较远处,随着车速的提高,动力响应反而有减弱的趋势。

3)路面等级对行车随机动荷载的影响最大,路面等级越差,行驶时车辆引起隧道的振动响应越强。随着路面等级由好变差,土体应力响应峰值翻倍增加。

4)相同工况作用下,砂土隧道中侧边土体振动应力响应峰值远大于软土隧道土层中的对应峰值,前者几乎为后者的6倍。当隧道处于砂土层时,土体应力随着距管片距离的增大迅速衰减,而在黏土层中的应力响应衰减较为缓慢。