基于回归分析和GA-BP神经网络算法的3D打印件弯曲性能预测

白鹤，杨鑫，杨瑞琦，刘亚明，赵峥璇，庞瑞，何石磊

(1.宝鸡职业技术学院机电信息学院，陕西宝鸡 721013；2.宝鸡石油钢管有限责任公司钢管研究院，陕西宝鸡 721008；3.国家石油天然气管材工程技术研究中心，陕西宝鸡 721008；4.宝鸡石油钢管厂职工子弟学校，陕西宝鸡 721008)

3D 打印技术是近些年来涌现出来并发展迅速的一项快速成型技术，它与工业机器人技术、人工智能技术一起称之为能带来“第三次工业革命”的核心技术[1-2]。熔融沉积成型(FDM) 3D打印技术的工艺原理是将加热熔融状态的丝材从打印机喷嘴中挤出并按照零件截面轮廓逐层堆积在工作台上成型[3-4]。由于其操作简单、成本低廉，并广泛使用具有良好环保特性的聚乳酸(PLA)材料，使得该项技术在教育、生物、医疗、航天航空等众多领域内得到广泛使用[5-7]。

随着经济的发展和社会的进步，人们对FDM 3D 打印制品的质量和性能要求越来越高，因此，如何提升FDM 3D打印制品的质量和性能也成了众多工程技术人员竞相研究的课题。李生鹏[8]根据正交试验设计对FDM 3D 打印件力学性能进行了检测，并用灰色关联分析法对制件质量和工艺参数之间关系进行探讨。郑小军[9]利用正交试验和极差分析，重点讨论了打印层厚、试样放置方式和成型角度三个方面对FDM 3D打印件拉伸性能的影响。孟陈力[10]研究了填充方式、层高度等因素单独对FDM 3D打印件力学性能的影响。穆存远、祝洲杰等[[11-12]则重点从FDM 3D打印路径规划方式方面探究了其对制件拉伸性能的影响。虽然针对FDM 3D打印制件力学性能的研究越来越多，但使用GA-BP神经网络来预测FDM 3D打印制件弯曲性能的研究却鲜有报道。

笔者采用回归分析、GA遗传算法优化BP神经网络以及传统BP神经网络算法，以不同FDM 3D打印工艺参数制备的25组试样弯曲性能数据为基础，开展了FDM 3D 打印件弯曲性能预测模型的创建，并通过比较模型预测数据和试验数据，确定了模型精度。本研究可为FDM 3D打印工艺进步和高质量制件制备提供参考。

1 试验部分

1.1 主要原料

PLA：Φ1.75 mm，北京CANⅤBOT 科技有限公司。

1.2 主要仪器与设备

FDM 3D 打印机：N750 笛卡尔斜角坐标系，北京CANⅤBOT科技有限公司；

电子万能材料试验机：AGS-X10KN，日本SHIMADZU公司；

游标卡尺：0～150 mm，哈尔滨量具刃具集团有限责任公司。

1.3 试样制备

弯曲试样根据GB/T 9341-2008标准进行制备，笔者选用标准中的推荐试样，其结构及尺寸如图1所示。首先使用计算机软件完成试样的三维建模，并输出为STL 格式文件。随后将STL 文件导入切片软件，输入工艺参数后进行切片，最后导出GCODE 程序进行打印。试验用3D 打印机喷嘴直径为0.4 mm，扫描路径与试样长度方向呈45°，热床50 ℃，试样首层厚度与末层厚度相同，均为1 mm，试样长宽平面水平放置，沿高度方向成型[13]。本次弯曲试验的试样共制备25组，每组由5个平行样组成，根据五因素四水平[L16(45)]的正交试验设计原则和BP 神经网络模型的搭建要求设计。表1 为正交试验水平、因素的具体设置。其中五因素分别为分层高度(A)、填充密度(B)、打印温度(C)、打印速度(D)以及外壳厚度(E)。

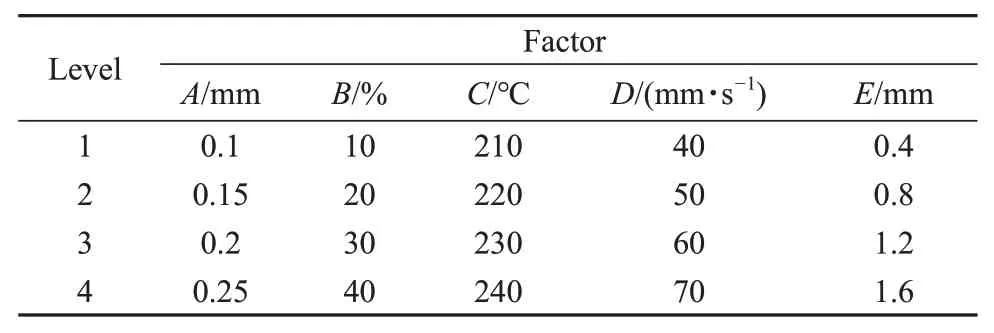
表1 正交试验水平因素设置表Tab. 1 Orthogonal test factor level table

图1 弯曲试样尺寸形貌及局部放大图Fig. 1 Dimensions and partial enlarged detail of flexural sample

1.4 试验方法

按照GB/T 9341-2008 要求，对25 组试样进行弯曲性能测试，试验选取加载速度2 mm/min，压头半径R=5 mm，跨距长度为64 mm。

1.5 试验结果

将每组平行试样的试验数据求平均值后记录为该组试样在相应因素水平下的弯曲性能指标，并将试样的弯曲性能指标作为分析样本，进行GA-BP神经网络、BP神经网络以及回归分析预测模型的搭建。试验结果见表2。

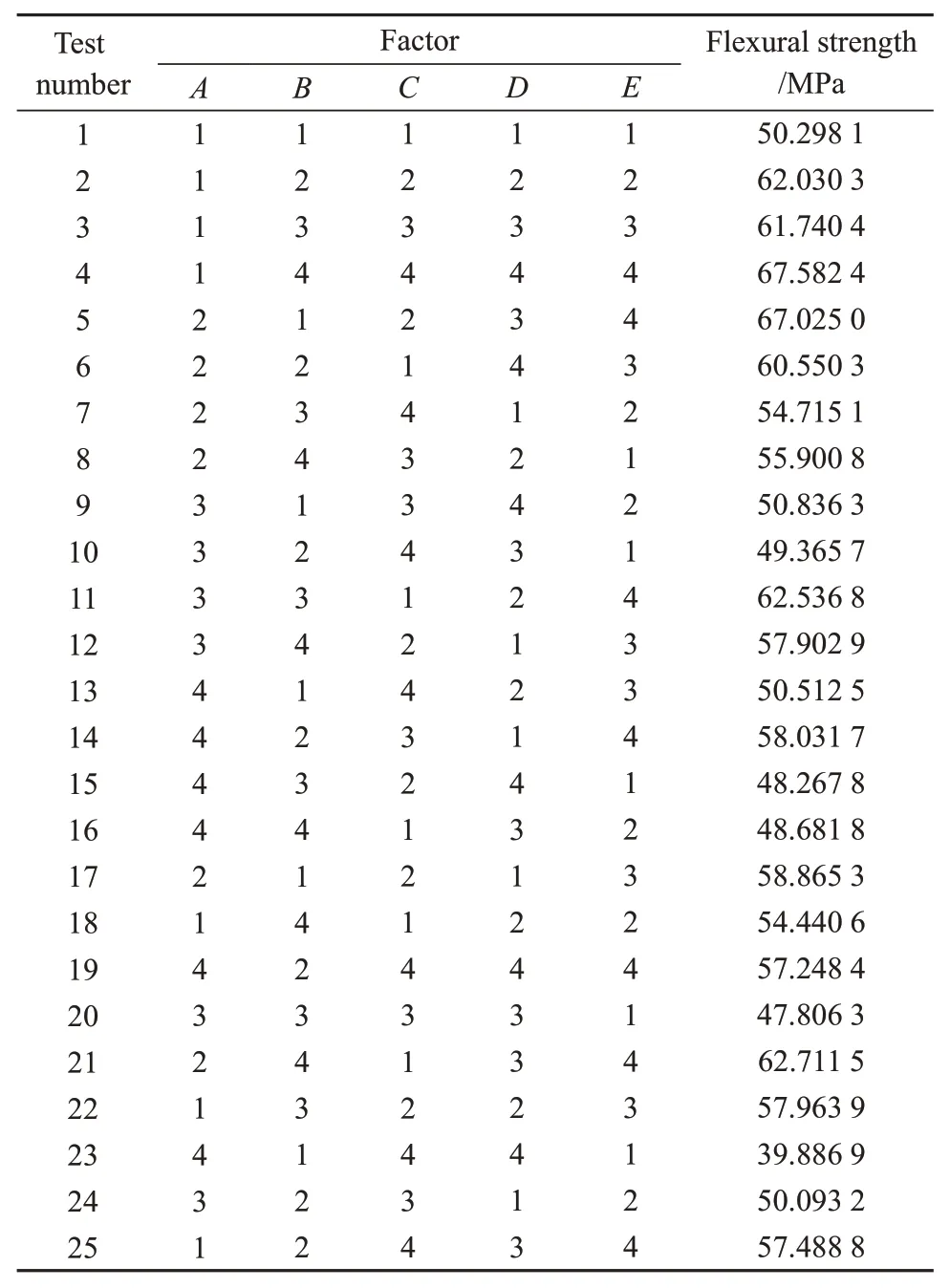
表2 试验方案及结果Tab. 2 Test scheme and results

2 GA-BP神经网络分析

2.1 GA-BP神经网络模型构建

BP神经网络是一种由大量神经元组成，且能够快速寻找最优解的非线性网络系统，其结构一般由输入层、隐含层和输出层组成，包括向前传播和反向传播两个过程，通过向前的信号传播和反向的误差传播，实现逐步修正各层权值，使误差不断减小，最终返回输入层。不断重复上述过程，直到满足终止条件[14-16]。但传统的BP 神经网络算法具有初始权值和阈值随机选择的特点，因此在进行训练时，易出现收敛于局部最小值、算法收敛速度慢或输出不稳定等问题。故需对其进行改进，以提高网络精度。使用GA 遗传算法对传统BP 神经网络的初始值进行寻优，可实现BP 神经网络以最优的权值和阈值进行训练，最终达到可靠预测精度[17]。GA遗传算法优化BP神经网络的流程图如图2所示。

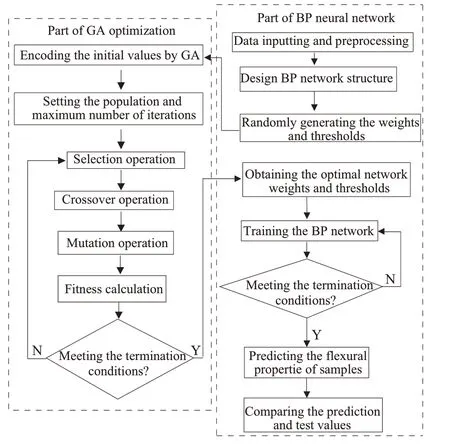
图2 遗传算法优化BP神经网络流程图Fig. 2 Flow chart of genetic algorithm optimized BP network

传统BP 神经网络模型一般由输入层、隐含层和输出层组成，一般在没有特殊限制的情况下，含有一个隐含层的神经网络模型便可以完成任意非线性的映射。只有当数据样本较多时，才会考虑增加隐含层的数量以减少网络规模。结合本次试验测试数据的特点和数量，笔者采用的BP 神经网络模型为传统的三层结构，即一个输入层、一个隐含层和一个输出层。输入层神经元个数n=5，输出层神经元个数m=1。隐含层神经元个数则结合经验公式(1)和试验法，确定为l=11[18]。故确定本次BP神经网络结构为5×11×1。其结构见图3所示。

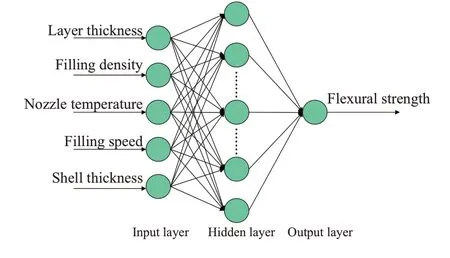
图3 BP神经网络模型Fig. 3 BP neural network structure diagram

本次GA-BP神经网络算法模型在传统BP神经网络模型算法的基础上，对其进行遗传算法优化，并通过公式(2)进行计算，最终可得到该神经网络模型初始的权值和阈值个数分别为66 个和12 个，编码长度为78。具体GA-BP 神经网络算法模型参数见表3。

表3 GA-BP神经网络算法模型设置参数Tab. 3 Parameter setting of GA-BP neural network algorithm model

式中：S为编码长度，n为输入层神经元个数，l为隐含层神经元个数，m为输出层神经元个数。

2.2 GA-BP神经网络的训练及验证

将制备的25 组试样弯曲性能检测数据分成两组，1#～20#为GA-BP 神经网络预测模型的训练样本，21#～25#则为测试样本。为进一步缩小由实验数据量纲不统一造成的网络预测误差，在进行网络学习和训练前，对试验数据进行归一化处理。将其置于[0，1]之间。具体操作方法见式(3)。

式中：X'为归一化之后的数据，X为归一化之前的数据，Xmax为向量中元素的最大值，Xmin为向量元素中的最小值。

在GA-BP网络模型进行训练过程中，当计算迭代到第四代之后，性能指标为7.83×10-10，达到了最佳值。GA-BP 神经网络模型预测数据与试验测试数据的对比情况见表4，不难看出，GA-BP神经网络模型的预测数据整体大于试验测试数据，但两组数据整体非常接近，说明该模型的预测效果良好。

表4 GA-BP神经网络模型预测数据与试验测试数据对比Tab. 4 Comparison between GA-BP neural network prediction value and experimental test value

3 预测模型对比与讨论

3.1 回归分析与BP神经网络模型的构建

利用数据分析软件，将本次试验的1#～20#检测数据作为数据样本进行线性回归分析并构建多元回归方程。具体方程结构式见式(4)：

式中：β0为常数项，β1，β2，β3，β4，β5则为偏回归系数，均为常数。X1，X2，X3，X4，X5则为自变量，对应正交试验中的五个因素。Y为试样弯曲性能的预测值。

根据最小二乘法原理，引入向量和矩阵，经回归分析后得到方程的常数项、偏回归系数、偏回归系数置信区间以及相应的检验统计量。具体分析结果见表5。得到的多元回归方程见式(5)。

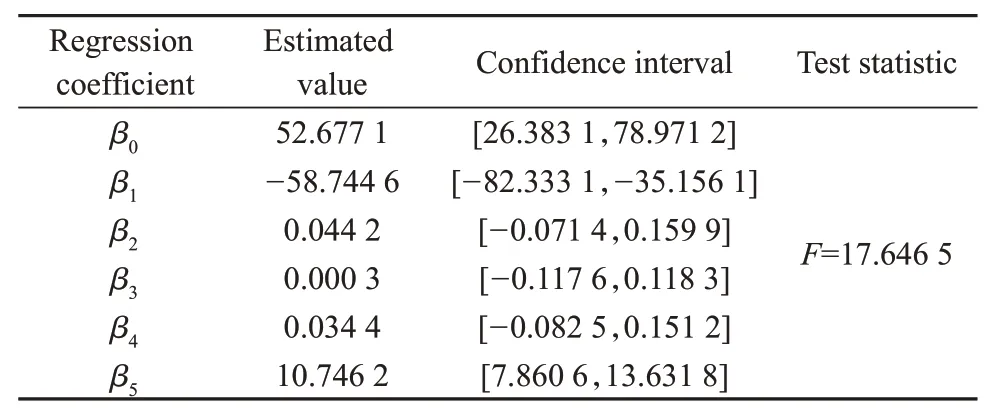
表5 回归模型计算结果Tab. 5 Calculation results of regression model

使用F检验法对多元回归方程进行显著性检验，从表5 可知，回归分析得到的检验统计量F=17.646 5，远大于F0.05的临界值，因此，说明该多元回归方程显著，可以使用。

与此同时，为了进一步验证GA 遗传算法是否对BP 神经网络寻优能力有所提升，因此建立一个与GA-BP 神经网络模型结构(5×11×1)一样的未经遗传算法优化的BP 神经网络模型，保持参数设置和训练样本一致，来进行试样弯曲性能的预测，其预测结果与GA-BP神经网络预测数据、多元回归方程预测数据以及试验测试数据进行对比，以此来评价三种预测模型的准确性。

3.2 三种预测模型精度对比

图4 为GA-BP 神经网络、传统BP 神经网络以及回归分析三种预测模型对21#～25#试样弯曲性能预测数据与试验测试数据的对比情况。从图4中不难看出，除BP 神经网络21#试样预测结果(58.766 MPa)低于试验测试数据(62.711 5 MPa)以外，其余所有预测数据均高于试验测试数据，但整体GA-BP神经网络模型的预测数据曲线与试验测试数据曲线更为接近，BP神经网络模型预测数据曲线与多元回归方程预测数据曲线接近，较GA-BP神经网络模型预测数据曲线和试验测试数据曲线位置更高。

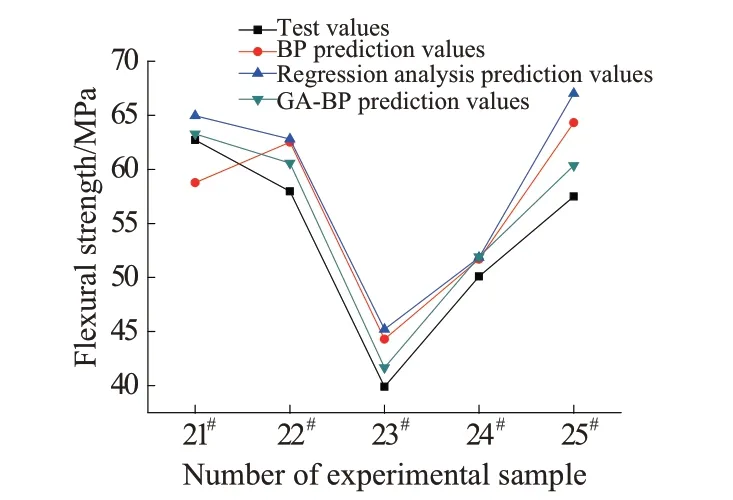
图4 三种预测模型预测数据与试验测试数据对比Fig. 4 Comparison of three models predictive value and experimental value

此外，从三种预测模型的误差对比情况(图5)来看，GA-BP神经网络模型预测误差数据曲线最平稳且误差值最小，范围为(0.91%～4.98%)，平均误差值3.71%，多元回归方程预测数据曲线波动幅度最大，范围(3.52%～16.57%)，平均误差值9.07%，BP 神经网络预测误差曲线与多元回归方程预测误差曲线形貌相似，整体波动相对较小，其误差范围为(3.16%～11.88%)，平均误差值8.05%。因此不难说明GABP 神经网络预测模型整体精度最高，BP 神经网络预测模型次之，多元回归方程预测精度最差。但BP神经网络预测模型与多元回归方程两者预测精度相差不大。

图5 三种预测模型预测误差对比Fig. 5 Comparison of prediction errors of three models

3.3 讨论

相较于传统的BP神经网络模型，经过GA遗传算法优化的BP神经网络模型拥有相对较高的预测精度，主要是因为GA 遗传算法采用了适者生存的法则，通过种群逐代演化和交叉遗传变异，逐代淘汰劣势个体，并最终筛选出最适应环境的最优个体，将其解码并以最优权值和阈值的方式赋给传统BP 神经网络，从而得到更加精准且稳定的预测结果。其次是由于本次传统BP神经网络模型在创建过程中，没有大量的训练数据，使预测结果与试验测试结果之间的差异增大。第三，进行回归分析时，由于试验测试数据在拟合过程中本身存在一定误差，从而导致回归方程精度下降，加之试样在进行尺寸测量的过程中，无法做到精确无误，最终导致预测误差增大。

4 结论

(1) 对比三种FDM 3D 打印制件弯曲性能的预测模型发现，GA-BP神经网络算法预测模型精度最高，预测误差范围为(0.91%～4.98%)，平均误差值3.71%，BP神经网络算法预测模型次之，预测误差范围为(3.16%～11.88%)，平均误差值8.05%，多元回归方程预测相对最差，预测误差范围(3.52%～16.57%)，平均误差值9.07%。

(2) 采用GA 遗传算法优化BP 神经网络模型，使BP 神经网络模型获得最优的权值和阈值，从而进一步提升BP 神经网络模型的预测精度和稳定性。

(3) GA-BP 神经网络预测模型可满足FDM 3D打印制件弯曲性能的预测要求，具有较高的实用性。