基于Box-Cox变换结合多种算法的风电机组数据预处理方法研究

韩则胤，王 宁，苏宝定，田元兴

(中广核风电有限公司，北京 100070)

0 引言

近年来，风电市场的迅猛发展，全球风电机组装机容量大幅增长，风电机组的后期维护问题也日渐凸显。风电机组通常处于偏僻且天气恶劣的环境中，其故障后维修成本高昂[1-3]。随着大数据分析技术和机器学习的快速发展，数据采集与监视控制(SCADA，supervisory control and data acquisition)系统中的远程监控和数据采集的功能在风力发电安全运行、特征分析、优化运行等相关应用研究中的地位逐渐凸显。风电场SCADA系统中的数据在采集、传输、存储等过程中不可避免会出现错误和遗漏等问题，风电机组在实际运行过程中会出现弃风限电的现象，导致所采集的数据质量欠佳，不利于后续对采集的数据进行相关的应用研究和分析[4-6]。因此，在数据应用分析之前，必须对所采集的数据进行数据预处理操作，以便为后面的分析和预测提供准确的数据信息。

近年国内外学者提出了多种异常数据识别清洗方法和故障预警策略。赵永宁等人提出一种基于四分位法和K-means聚类法的混合方法对异常数据进行筛选和清洗。采用两次四分位法来识别并清洗分散型数据，采取K-means聚类法来识别并清洗堆积型数据，该方法可以有效地剔除弃风限电产生的异常数据，具有一定的实用性和通用性[7]。马然等人根据风速-功率曲线和转速-功率曲线提出一种基于经验Copula-ECMI的方法筛选适宜的特征参数进行监测，基于各参数的时序特征与概率分布构建Copula数据清洗模型，依次对堆积型和分散型的异常数据进行剔除[8]。沈小军等人根据风电机组功率曲线中离群值分布特点，提出一种基于变点分组算法和四分位数算法相结合的算法，该算法可以对离群值识别和剔除，但是此算法对多种控制参数存在要求[9]。Ouyang T等人在假设监测到的风速-功率曲线数据概率分布服从正态分布的前提下，提出采用支持向量机原理建立功率边界模型的方法[10]。文献[11]、[12]中所提出的异常数据清洗方法也是以风速-功率曲线的概率分布服从或者近似服从正态分布为前提。Taslimi-Renani E等人提出一种利用修正双曲正切函数来表示风电机组的功率曲线的模型，在不同均值下可以构建不同标准差的阈值模型，从而剔除超出阈值的异常数据，经检验所提出的模型具有一定实用性[11]。Villsnueva D等人则是提出一种利用蒙特卡罗模拟技术重现基于正常模型的方法，重现的模拟模型用于对风电机组长期评估[12]。Gill S等人基于Copula统计理论建立风速-功率联合概率模型，对于风电机组的早期故障的识别有很强的实用性[13]。潘雄提出基于混合Copula函数建立风电场模型，该模型更注重针对不同风电场的通用性[14]。Liang G等人提出一种基于不相似与不确定性能量最小化的WPC异常数据清洗算法，该算法将监测的数据转化为数字图像，运用图像分割的方法来清洗异常数据，大量实验证明了该算法具有优越性[15]。Huan等人提出一种基于图像的异常数据清洗算法，人为将异常数据定义为负点、分散点和堆积点3种类型，先将大于切入风速且功率小于零的负点进行剔除，利用数学形态学运算提取表征正常数据的WPC二值图像的主成分，对分散点和堆积点进行像素识别和标记，经过实验验证了该方法的高效性和通用性[16]。朱倩雯等人运用多点三次样条插值的方法对数据缺失的情况进行数据重构，进而得到完整的时间序列，具有较强的实用性[17]。胡阳等人提出分段三次Hermite插值法对于缺失数据进行重构[18]，但是插值重构的方法对于连续缺失达到一定数量的数据，其重构值与真实值会出现较大的偏差，这类方法可能会对实验结果有较大的影响。

综上，国内外学者提出的数据预处理方法主要从几个方面入手：基于不同特征的异常数据，例如分散型异常数据和堆积型异常数据，选择适宜的数据清洗方法进行数据预处理[19]；基于风速-功率曲线的近似服从正态分布的特性进行研究，该类方法可以提高SCADA系统中有效数据的占比，能够实现数据质量的改善；基于风电机组的实际输出功率概率分布特性的统计分析，确定一定置信条件下输出功率变化范围，识别、剔除异常数据；基于图像的异常数据清洗算法，将监测数据转化为图像问题，可以更直观的进行数据清洗；基于数据缺失的情况进行研究，可以选择适宜的数据插值重构的方法进行数据预处理，该方法有一定的局限，当风电机组的样本数据出现大量缺失数据的情况时，重构数据的效果与实际监测效果有很大的误差，需要继续研究更优秀的数据插值重构法以解决此类问题。本文提出一种将Box-Cox变换与以正态分布为前提的异常值清洗算法相结合的方法，对原始数据进行预处理。运用Box-Cox变换分别与Bin算法、肖维勒准则、狄克逊准则和格拉布斯准则相结合的方法进行数据预处理，经过实例验证，所提方法对原始数据有较好了数据预处理效果。

1 基于Box-Cox变换的风电机组数据预处理

风速-功率曲线是描述风电机组运行时不同风速和输出功率关系的数据分布曲线。根据风速-功率曲线，能够非常直观的监测风电机组的运行状态，该曲线可以显示风电机组的性能和发电能力[60]。许多数据预处理方法是建立在数据处于正态分布的基础上才能进行预处理操作，例如格拉布斯准则、狄克逊准则、拉依达准则、肖维勒准则、Bin算法等。由于风电机组的风速-功率曲线并不是严格意义上的正态分布，因此对原始数据进行Box-Cox变换，使原始数据呈现正态分布，以便于参与后续的数据预处理的工作，为后续研究提供更加准确的数据。

1.1 Box-Cox变换基本原理

Box-Cox变换是由Box和Cox两人共同提出的模型，该模型可以将不满足正态分布的数据经过Box-Cox变换后使其呈现正态分布的状态。

设原始数据为y={y1，y2，y3，L，yn}，对原始进行Box-Cox变换：

(1)

式中，λ是一个待定的变换参数。

对原始数据进行Box-Cox变换后，可以得到：

(2)

式中，n表示Box-Cox变换后数据的个数。

通过对原始数据的变换，使得变换后的数据与变换参数λ有了对应的联系。因此，Box-Cox变换是通过对λ的合理选择，使其变换后的数据呈现正态分布的状态。因此对的选择是很重要的。

对于λ的选择可以用极大似然法来估计。首先，构造似然函数L(λ)：

(3)

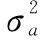
对式(3)中所有的λ，有：

(4)

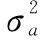
(5)

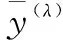
经推导可得到如下方程：

(6)

每一个变换参数λ对应的y(λ)都可得到相应的L(λ)。通过寻优，可以得到使得L(λ)取得最大值的变换参数λ*，则λ*即为Box-Cox变换最终的变换参数。

1.2 数据预处理方法

1.2.1 Bin算法基本原理

Bin算法的基本原理：记风电机组的切入风速Vmin和切出风速Vmax，将风速区间[Vmin，Vmax]划分成多个小区间，依照风速大小将各个风速数据划分到各小区间中，再对各个小区间中的数据进行统计，最后用统计得到的各个小区间中的数据统计值进行分析。

设风电机组切入风速为Vmin，切出风速为Vmax，风速区间为[Vmin，Vmax]。将风速区间以0.5 m/s的间隔划分为N个小区间：

(7)

式中，N为正整数。

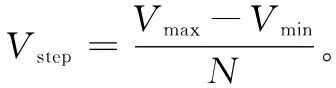
(8)

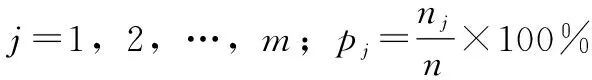
(9)

对单个SCADA数据的描述采用的是期望值而不是平均值。这种方法的优点是期望值减少了数据中离群值造成的统计误差，而平均值由于没有考虑这些离群值的概率分布会造成较大误差。

1.2.2 肖维勒准则基本原理

肖维勒准则是以检测样本服从正态分布为前提的方法，其原理：对n个实验数据进行多次实验，统计实验中n个实验数据的误差值出现可能性为零的数据点的个数，计算这些数据的概率。计算数据概率的公式为：

(10)

式中，n表示实验数据个数；Zc为肖维勒系数；可以根据式(10)总结出表示n和Zc关系的肖维勒系数表。

计算测量数据的算数平均值x、偏差vi和标准差σ：

(11)

(12)

(13)

式中，xi表示第i个数据；n表示实验数据个数。

1.2.3 狄克逊准则基本原理

狄克逊准则是以检测样本服从正态分布为前提的数据预处理方法，其基本原理是将服从正态分布的检测数据按照从大到小排列，则检测样本中可能为异常数据的样本为或者，其中为样本数量。计算不同样本数量对应的极差比，如表1。

表1 不同的样本数量n的极差比

根据表1，针对不同的样本数量n来计算出对应的极差比γ和γ*。

选定显著性水平α，显著性水平用于估计总体参数在某区间内可能犯错的概率，狄克逊准则中的显著性水平α通常选取0.05或0.01，本文狄克逊准则的显著性水平α选为0.01。

1.2.4 格拉布斯准则基本原理

格拉布斯准则通过计算一组实验数据的残差，来判断该组数据是否含有异常值。运用格拉布斯准则的前提是采集的检测样本服从正态分布或者近似服从正态分布。格拉布斯准则的基本原理：

将检测数据按照x1≤x2≤…≤xn的顺序从小到大排列，每次检测总是先怀疑最大的数据和最小的数据是否为异常值。选定显著性水平α，同狄克逊准则相似，格拉布斯准则中的显著性水平α通常选取0.05或0.01，本文格拉布斯准则的显著性水平α选取为0.05。

计算测量值对应的残差：

(14)

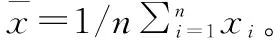
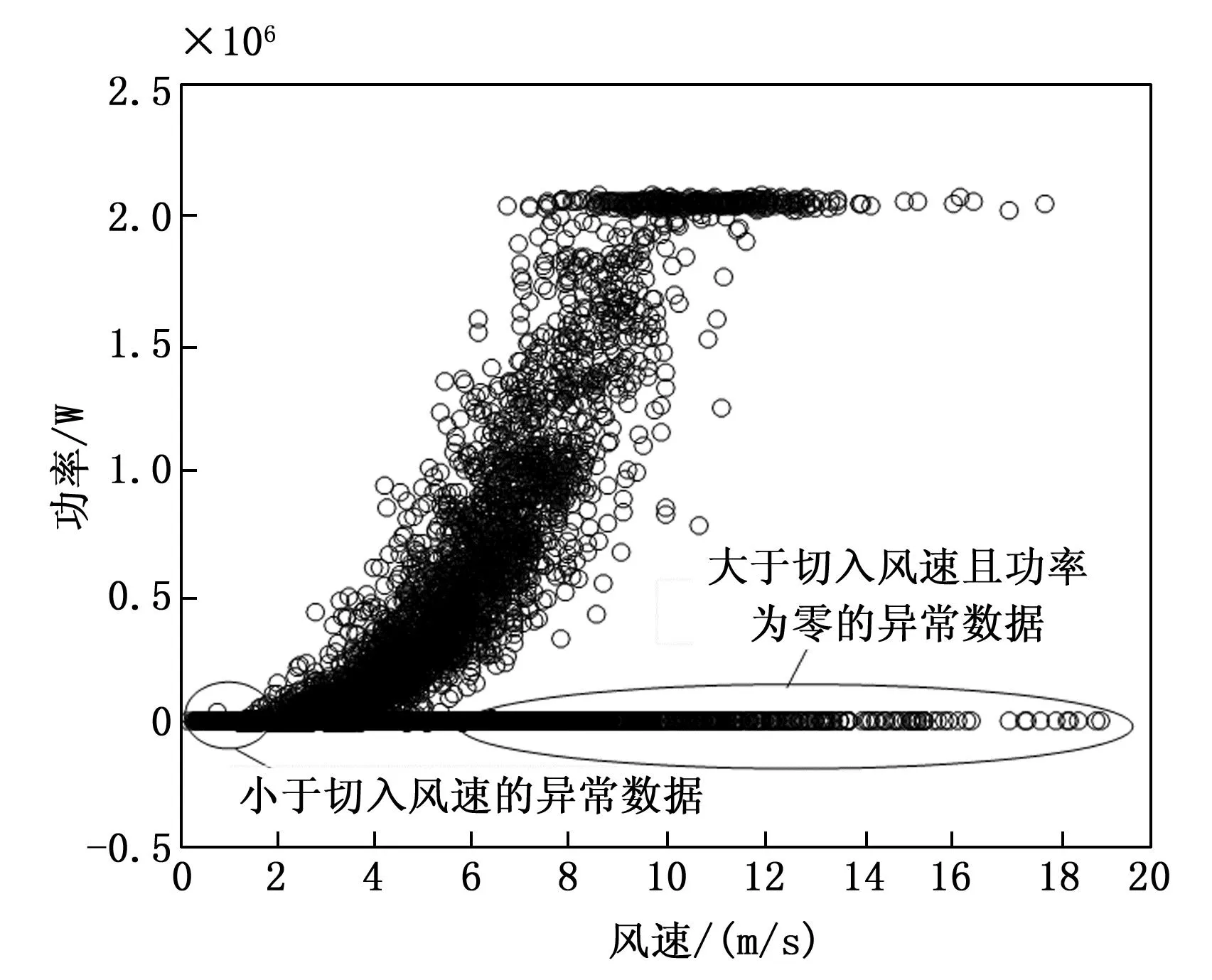
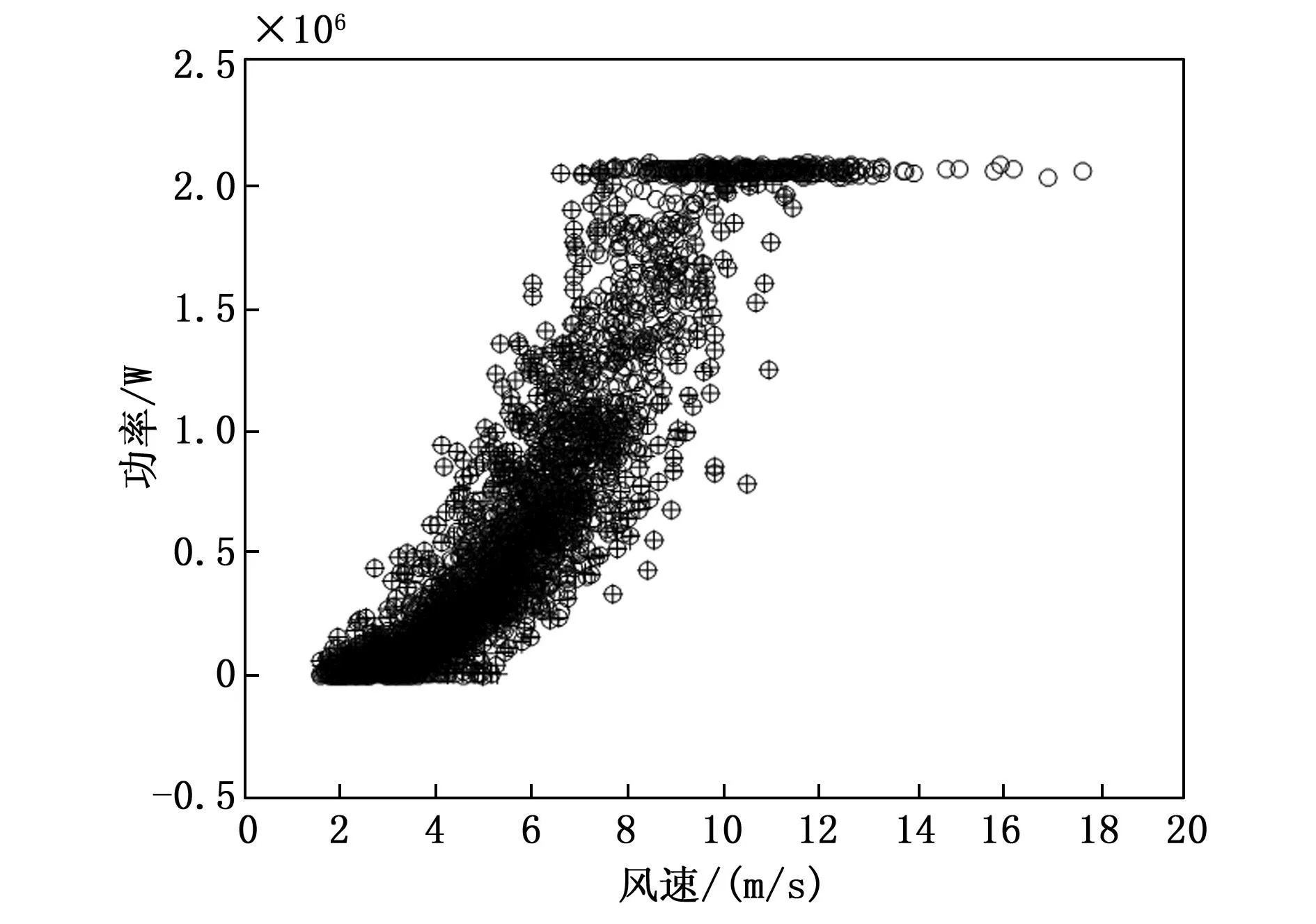
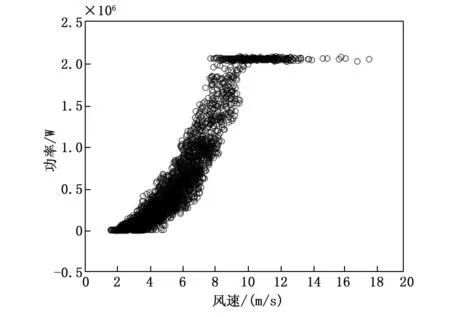
查询格拉布斯准则临界值T(α，n)表，找出对应n和α的T(n，α)值。当T≥T(n，α)时，认为怀疑的测量值是异常数据，应当予以舍弃；当T

2 实例分析

2.1 数据来源

本文的实验数据选取自张家口某风电场的实际运行数据，将该风电场的A12号风电机组作为研究对象，采用A12号风电机组在2018年9月26日到2019年1月26日的实际运行数据来测试本文所提出的方法。在SCADA数据中，含时间变量的数据共有70类，与齿轮箱相关的变量为5个，与发电机相关的变量为9个，与主轴相关的变量为2个、与变桨系统的相关变量为33个。

该风电场的风电机组的类型为变速恒频双馈异步风电机组，其基本参数为：风电机组额定功率为2 000 kW，切入风速为2 m/s，切出风速为20 m/s。经过研究分析，挑选出其中的5个与齿轮箱的相关的变量进行分析研究。5个齿轮箱的相关变量分别为：齿轮箱温度、风速、发电机输出功率、上一时刻的齿轮箱温度、环境温度。

2.2 数据预处理

将风速为[0，20]的区间以0.5 m/s为步长间隔划分为40个小区间，如图1所示。当环境风速小于风电机组的切入风速时，没有达到风电机组并网发电的最低风速，因此将环境风速小于切入风速所测得的功率数据进行剔除。当环境风速大于切入风速时，风电机组开始并网发电，由于弃风限电、设备停机检修等因素的影响，产生一系列环境风速大于切入风速但是功率为零的异常数据。如图1所示，这类数据在图中堆积在功率为零的位置，将这种异常数据进行剔除，这一操作可以剔除大量异常数据，以便提高后续工作的速度和实验效果。

图1 风速-功率曲线异常数据划分示意图

剔除环境风速小于切入风速的数据和环境风速大于切入风速且功率为零的数据，如图2。

图2 剔除异常数据后的风速功率图

2.3 Box-Cox变换和Bin算法相结合的数据预处理分析

使用Bin算法对异常数据进行数据清洗，检测结果如图3所示。从图3中可以看出，利用Bin算法对样本数据进行检测，可以检测出风速-功率曲线中的部分离散数据。Bin算法是将样本数据近似看作正态分布的基础上进行的分析，由于风速-功率曲线并不是严格意义上的正态分布曲线，所以检测结果难免会出现误差。

图3 使用Bin算法进行数据清洗的检测结果图

使用Box-Cox变换与Bin算法结合的方法对异常数据进行清洗，检测结果如图4所示。

图4 使用Box-Cox变换和Bin算法相结合的数据清洗检测结果图

图4中被“十字”标出的为异常数据，圆圈为正常数据。对比图3和图4可以看出，图4中检测出的异常数据明显比图3中的多，利用提出的Box-Cox变换和Bin算法结合的方法对样本数据进行检测，可以更全面地识别异常数据。Box-Cox变换可以提高数据曲线的正态性，使得风速-功率曲线中的数据呈现正态分布，再运用Bin算法进行检测，异常数据清洗效果明显提高了。

采用Box-Cox变换与Bin算法相结合方法对异常数据进行清洗后的NSET建模数据集，如图5。经过对原始数据的预处理，经统计共有2 034个异常数据条目被清洗，最终得到5 845个数据条目用来进行NSET建模实验。

图5 基于Box-Cox变换与Bin算法相结合方法的NSET建模数据集

2.4 Box-Cox变换和肖维勒准则相结合的数据预处理分析

使用肖维勒准则对异常数据进行数据清洗，检测结果如图6所示。

图6 使用肖维勒准则进行数据清洗的检测结果图

图6中被“十字”标出的为异常数据，圆圈为正常数据。利用肖维勒准则对实验数据进行检测，同Bin算法清洗异常数据的效果相似，肖维勒准则同样可以检测出风速-功率曲线中的部分离散数据为异常数据。因为肖维勒准则的检验前提是样本数据服从或近似服从正态分布，而风电机组的风速-功率曲线并不是严格意义上的正态分布曲线，所以检测结果难免会存在误差。

使用Box-Cox变换与肖维勒准则相结合的方法对异常数据进行清洗，检测结果如图7所示。对比图7和图6可以看出，利用Box-Cox变换和肖维勒准则相结合的方法对样本数据的检测效果要比只使用肖维勒准则的效果好，前者可以更加充分地识别和剔除异常数据。利用Box-Cox变换提高风速-功率曲线的正态性，使得风速-功率曲线中的检测数据呈现正态分布，再运用肖维勒准则对数据进行检测，异常数据的检测效果明显提高。

图7 使用Box-Cox变换和肖维勒准则相结合的数据清洗检测结果图

采用Box-Cox变换和肖维勒准则相结合的方法对异常数据进行清洗后可用于机组故障预警建模的数据集，如图8所示。

图8 基于Box-Cox变换和肖维勒准则相结合方法的NSET建模数据集

对原始数据进行数据预处理后，经统计共有1 752个异常数据条目被清洗，最终共有6 127个数据条目用于进行故障预警建模实验。

2.5 Box-Cox变换和狄克逊准则相结合的数据预处理分析

使用狄克逊准则对异常数据进行数据清洗，检测结果如图9所示。利用狄克逊准则对实验数据进行检测，可以检测出风速-功率曲线中的部分离散型数据为异常数据。狄克逊准则检测异常数据的前提是样本数据服从正态分布，由于风电机组的风速-功率曲线并不是严格意义上的正态分布曲线，所以检测结果会存在一定的误差。

图9 使用狄克逊准则进行数据清洗的检测结果图

使用Box-Cox变换与狄克逊准则相结合的方法对异常数据进行清洗，检测结果如图10所示。

图10 使用Box-Cox变换和狄克逊准则相结合的数据清洗检测结果图

对比图10和图9可以看出，利用Box-Cox变换和狄克逊准则相结合的方法对样本数据的检测效果要比单独使用狄克逊准则的效果好，前者检测出的异常数据更多。使用Box-Cox变换提高风速-功率曲线的正态性，再运用狄克逊准则对数据进行检测，异常数据的检测效果明显得到提高。

对原始数据进行数据预处理后，经统计共有2 271个异常数据条目被清洗，最终共有5 608个数据条目用于进行NSET建模实验。采用Box-Cox变换和狄克逊准则相结合的方法对异常数据进行清洗后可用于NSET建模的数据集，如图11所示。

图11 基于Box-Cox变换和狄克逊准则相结合方法的NSET建模数据集

2.6 Box-Cox变换和格拉布斯准则相结合的数据预处理分析

使用格拉布斯准则对异常数据进行数据清洗，检测结果如图12所示。

图12中被“十字”标出的为异常数据，圆圈为正常数据。利用格拉布斯准则对实验数据进行检测，与前面3种数据预处理方法的清洗异常数据效果相似，格拉布斯准则同样可以检测出风速-功率曲线中的部分离散型数据为异常数据。格拉布斯准则检测异常数据的前提同样需要样本数据服从正态分布，而风速-功率曲线是近似于正态分布的曲线，并不是严格意义上的正态分布，运用格拉布斯准则检测异常数据的会存在一些误差。

进行Box-Cox变换和格拉布斯准则相结合的方法对异常数据进行数据清洗，实验结果如图13所示。

图13 使用Box-Cox变换和格拉布斯准则相结合的数据清洗检测结果图

通过图13可以看出，使用Box-Cox变换与格拉布斯准则相结合的方法比单独使用格拉布斯准则对异常数据检测的效果明显要好。先进行Box-Cox变换以提高被测数据的正态性，使得风速-功率曲线中的检测数据呈现标准正态分布，再运用格拉布斯准则对数据进行检测，通过实验结果可以观察到，异常数据的检测效果得到了提升，清洗程度更加充分。

采用Box-Cox变换和格拉布斯准则相结合方法对异常数据进行清洗后可用于NSET建模的数据集，如图14。

图14 基于Box-Cox变换和格拉布斯准则相结合方法的NSET建模数据集

对原始数据进行数据预处理后，经统计共有2 386个异常数据条目被清洗，最终共有5 493个数据条目用于进行NSET建模实验。

2.7 实验结果分析

本文以风电机组的齿轮箱为研究主体，将齿轮箱的温度、风速和发电机输出功率等参数作为监测参数进行实例分析。因为风电机组的风速-功率曲线的概率分布类似正态分布但不是标准的正态分布曲线，Box-Cox变换可以将检测数据变换为正态分布。首先将原始数据进行Box-Cox变换，以提高风速-功率曲线的正态性。然后分别使用Bin算法、肖维勒准则、狄克逊准则和格拉布斯准则4种方法对变换后的数据进行检测，检测并剔除异常数据。对比图3与图4、图6与图7、图9与图10、图12和图13，可以观察出使用Box-Cox变换的混合方法所检测出的异常值比未使用Box-Cox变换的方法检测出的异常值多，明显使用Box-Cox变换的方法对异常数据检测效果更好。而且可以从4种异常数据清洗方法的检测结果中观察到，格拉布斯准则对于异常数据的清洗效果最好，狄克逊准则和Bin算法次之，肖维勒准则虽然最简便易懂但是检测效果不是很好。但是对Box-Cox变换后的数据进行实验时，格拉布斯准则和狄克逊准则所用的时间比较长，Bin算法所用的时间最短。由分析可知格拉布斯准则和狄克逊准则并不适合应用于实际环境中，因为对大型风电场的海量数据，这种预处理需要很长时间的方法的实用性不强。

经过数据预处理后的四组数据集可为机组故障预警建模提供数据基础。

3 结束语

针对风电机组的故障预警提出了一种混合算法的数据预处理的方法，该方法是基于以风速-功率曲线中的数据呈现正态分布为前提的数据预处理算法，利用Box-Cox变换使原始数据变换呈现正态分布，再分别结合Bin算法、肖维勒准则、狄克逊准则和格拉布斯准则进行研究分析。通过实验分析可知：肖维勒准则的算法简单且检测时间短但是对于异常数据的清洗效果较差；狄克逊准则和格拉布斯准则对于异常数据的清洗效果较好但是处理时间较长，对大型风电场的海量数据，这种方法的实用性较差。在这4种算法中，Bin算法的优势比较明显，但是此算法仍有优化的空间，值得进一步研究。