基于MDS和改进SSA-SVM的高速铁路道岔故障诊断方法研究

王彦快，米根锁，孔得盛，杨建刚，张 玉

(1.兰州交通大学 铁道技术学院，甘肃 兰州 730000；2.兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；3.中国铁路兰州局集团有限公司 兰州电务部，甘肃 兰州 730000；4.北京全路通信信号研究设计院集团有限公司，北京 100070；5.国网甘肃省电力公司电力科学研究院，甘肃 兰州 730070)

道岔作为轨道连接设备是高速铁路(以下简称“高铁”)综合维修段重点关注的设备之一,经统计其维护工作量约占工电供结合部设备维护工作量的1/3以上,道岔故障数约占铁路信号设备故障总数的40%以上,其中机械故障占道岔故障总数的70%以上[1-3]。因此,实现道岔智能故障诊断、制定合理的维修策略将是提高维修效率的重要手段。目前“周期修”和“故障修”结合仍是道岔设备的主要维护模式,维修人员通过信号集中监测(centralized signaling monitoring,CSM)系统的监测数据,依据专业知识和工作经验分析道岔工作状态,并辅助维修道岔。该模式存在故障延时长、故障诊断准确率较低、劳动强度较大等缺陷,且易造成“欠维修”和“过维修”,维修存在局限性[4-5]。

近年来,国内外学者针对道岔设备的故障诊断开展了相关研究:杨菊花等[6]建立了基于CNN-GRU方法的道岔故障诊断模型;钟志旺等[7]提出基于主题模型PLSA和SVM的道岔设备故障特征提取与诊断方法;许庆阳等[8]建立了不同故障模式下的HMM模型,描述每一种退化状态之间的状态转移,实现道岔健康状态监测与诊断。基于以上研究,本文提出基于多维尺度缩放法(multiple dimensional scaling,MDS)和改进麻雀搜索算法(sparrow search algorithm,SSA)优化支持向量机(support vector machine,SVM)的高铁道岔故障诊断方法:从时域、频域、小波包能量熵3方面提取特征指标,其中小波包能量熵包含有瞬变成分的故障信号特征信息[9];通过MDS降维后最大限度地保留原高维数据所含信息量;SVM算法较深度学习算法在解决小样本数据方面具有一定优势[10],而采用改进SSA优化SVM算法,一方面增加种群的均匀性和多样性,另一方面避免SVM中惩罚因子c和核函数方差g选取的主观性,从而降低训练过程中陷入局部最优的概率,并提高故障诊断准确率[11]。具体实现过程:首先以ZDJ9型道岔转换功率曲线为研究对象,提取时域、频域及小波包能量熵3方面特征指标;其次采用MDS对高维特征指标降维优化,以低维特征空间构造的欧氏距离组成道岔特征指标向量;最后建立基于改进SSA-SVM算法的高铁道岔故障诊断模型,并验证该模型的可行性和高诊断准确率。

1 道岔转换功率曲线

1.1 正常曲线

由于道岔转换功率曲线不仅能够反映道岔转换时的电气特性、所受阻力大小以及机械性能,更能体现道岔的实际工作状态[12],因此,本文选择道岔转换功率曲线为研究对象。道岔正常转换功率曲线见图1。图1中,根据ZDJ9型转辙机动作时间t的先后顺序,其功率P曲线分为启动(0—t1)、解锁(t1—t2)、转换(t2—t3)、锁闭(t3—t4)、缓放(t4—t5)等5个阶段。在启动阶段,电机启动,断开道岔表示电路,其功率在短时间内增大,在0.32 s左右出现一个650～1 080 W的尖峰;解锁阶段,功率至尖峰点后迅速下降,密贴尖轨开始动作;转换阶段,尖轨移动,功率曲线比较平滑;锁闭阶段,尖轨移动密贴于基本轨,外锁闭装置锁闭尖轨位置,自动开闭器接点转换,同时断开启动电路而接通表示电路,断相保护器无电流通过,使保护继电器落下;缓放阶段,由于1DQJ的缓放,产生200 W左右的曲线“小台阶”;在t5时间点,1DQJ缓放结束,停止记录道岔功率曲线[13-14]。

图1 道岔正常转换功率曲线

1.2 典型故障曲线

经现场调研,分析并总结出7种典型道岔故障功率曲线F1～F7,见图2。依据道岔转换功率曲线波动及转换时长,进一步分析总结出故障现象及故障原因,见表1。

表1 道岔典型故障模式

图2 道岔典型故障功率曲线

2 道岔特征指标提取和降维

提取道岔功率曲线样本数据的时域、频域特征指标,同时对道岔功率曲线样本数据进行小波包分解,提取小波包能量熵,组成特征指标向量。由于特征指标之间存在相似性,故采用MDS方法进行降维优化。

2.1 道岔特征指标提取

1)时域特征指标提取

由于在不同故障类型下,道岔功率曲线在0—t2、t2—t3、t3—6.4 s 3段表现出的故障特点也不同,因此结合图2中F1、F2型道岔故障功率曲线在不同时间段出现功率“鼓包”的特点,为区分以上2种故障,又将道岔转换阶段平均划分为3个小区段,最终依次提取5个区段的平均值、均方根值、方根幅值、绝对平均值、偏斜度、峭度、方差、最大值、最小值、峰峰值、波形因子、峰值因子、脉冲因子、裕度因子、偏斜度因子等15个时域特征指标。

2)频域特征指标提取

为能够全面提取故障功率曲线中的细微变化,将道岔功率曲线数据经过快速傅里叶变换(FFT)后,依次提取功率曲线各段频谱的均值、功率、重心频率、平均频率、根方差频率、均方根频率、标准差频率、最大幅值、根方差幅值、平均相角、最大相角、能量、相角极差等13个频域特征指标。

3)小波包能量熵特征指标提取

小波包能够同时在低频和高频带内对信号进行分解,并根据信号特性和分析要求自适应选择相匹配的频带和频谱,且各分解频带内的信号相互独立、无冗余、不疏漏;而能量熵表示信号中出现的状态数目的可能性及相应概率,可用于评估信号的复杂性,有效地从信号中提取信息[9]。为能够准确提取含有瞬变成分的故障信号特征信息,选择对道岔功率曲线数据进行小波包分解,计算小波包能量熵,并结合时域、频域特征指标,构建道岔故障特征指标向量。小波包能量熵的实现思路:道岔功率信号经过多层小波包分解,将信号投影到一组互相正交的小波基函数构成的空间上,并将总能量划分到若干个互不重叠的频率区间内,经多通道滤波,大大消减信号之间的干扰[15-16]。

设对道岔功率信号S进行k层小波包分解,得到2k个小波包系数X(k,i),其中i为第k层的第i个节点,i=0,1,…,2k-1。

对应小波包系数X(k,i)的重构信号记为W(k,i),则总信号W为

W=W(k,0)+W(k,1)+…+W(k,2k-1)

(1)

重构信号对应的能量记为E(k,i),其计算式为

(2)

式中:d为道岔功率信号S的总长度。

信号的总能量Ek可以表示为

(3)

每个节点对应的重构信号能量占据总能量的比例记为P(k,i),其计算式为

(4)

P(k,i)的大小反映出第k层中各个频带的能量分布。根据香农定理,各个节点对应的小波包能量熵T(k,i)为

T(k,i)=-P(k,i)log2P(k,i)

(5)

则k个频带对应2k个节点的小波包能量熵组成2k维特征指标向量T,即

(6)

2.2 道岔特征指标降维

通过计算道岔功率曲线数据的时域、频域、小波包能量熵特征指标得到一个高维数据样本,虽然高维数据可以完整体现故障特征信息,但在高维空间中特征参数之间具有很大的相关性和冗余性,将直接影响道岔故障诊断模型的训练速度和诊断准确率,所以需要进一步对特征指标降维。目前常用的典型降维方法有:主成分分析(principal component analysis, PCA)、核主成分分析(kernel PCA, KPCA)和MDS降维。其中,PCA、KPCA方法为达到降维效果只保留方差大的主成分,导致可能丢失方差小的主成分中对分类结果有影响的特征;KPCA方法需要选取核函数并设置核函数参数,一般根据实际问题人为设置,受主观因素影响较大;而MDS方法利用成对的样本之间的相似度提取低维空间的特征,使得在低维空间中各样本之间的距离与其在高维空间中的距离保持高度的相似性[17]。鉴于此,本文结合道岔功率曲线的特点,采用MDS方法进行降维,实现步骤如下:

Step1采用min-max标准化对道岔特征指标样本数据做归一化预处理,以消除特征指标数据量纲不一致对故障诊断结果的影响。

Step2计算样本间的欧氏距离,建立距离矩阵。

Step3计算降维后样本的内积矩阵。

Step4对距离矩阵的双重中心化矩阵进行奇异值分解,并按照从大到小的顺序排列特征值,选取前o个特征值对应的特征向量构成矩阵Uo,组成的对角矩阵为Λo,降维后的样本X为

(7)

Step5评价函数的建立。道岔故障特征指标个数o为最终的降维维度,而对o的设定,一方面需要考虑能够有效降低道岔功率曲线样本的特征维度,另一方面也要保证低维样本数据能够较全面反映道岔设备的故障特征。为此,设置不同维度值o,计算评价函数值r,绘制r值变化趋势,r值越小,表示降维后的数据样本包含的道岔故障特征信息越完整[18]。r的计算式为

(8)

式中:m为样本数;d1ab、d2ab分别为降维前后各道岔功率曲线样本间的欧氏距离。

3 改进SSA-SVM道岔故障诊断模型

3.1 SSA算法原理

SSA算法是由Xue等[19]于2020年提出的一种新型群体智能优化算法,通过模拟麻雀觅食过程获得最优参数c和g。该算法与其他优化算法相比较,具有收敛速度快、搜索精度高、鲁棒性强等优点。其实现原理为:将整个麻雀群分为发现者、跟随者和侦查者3个群体,其中发现者和侦查者各占种群的10%～20%,其余均为跟随者。发现者搜索能力强,引导整个种群搜索和觅食;跟随者通过跟随发现者搜寻食物以获得更好的适应度;侦查者通过监视发现者以提高自身捕食率,当遇天敌威胁时,发出预警信号,种群做出反捕食行为。

在SSA算法中,假设搜索空间大小为D维,麻雀数量为N只,则第e只麻雀在该搜索空间中的位置Ye为

Ye=[ye,1,…,ye,h,…,ye,D]e=1,2,…,N

(9)

式中:ye,h为第e只麻雀在h维的位置。

发现者位置更新为

(10)

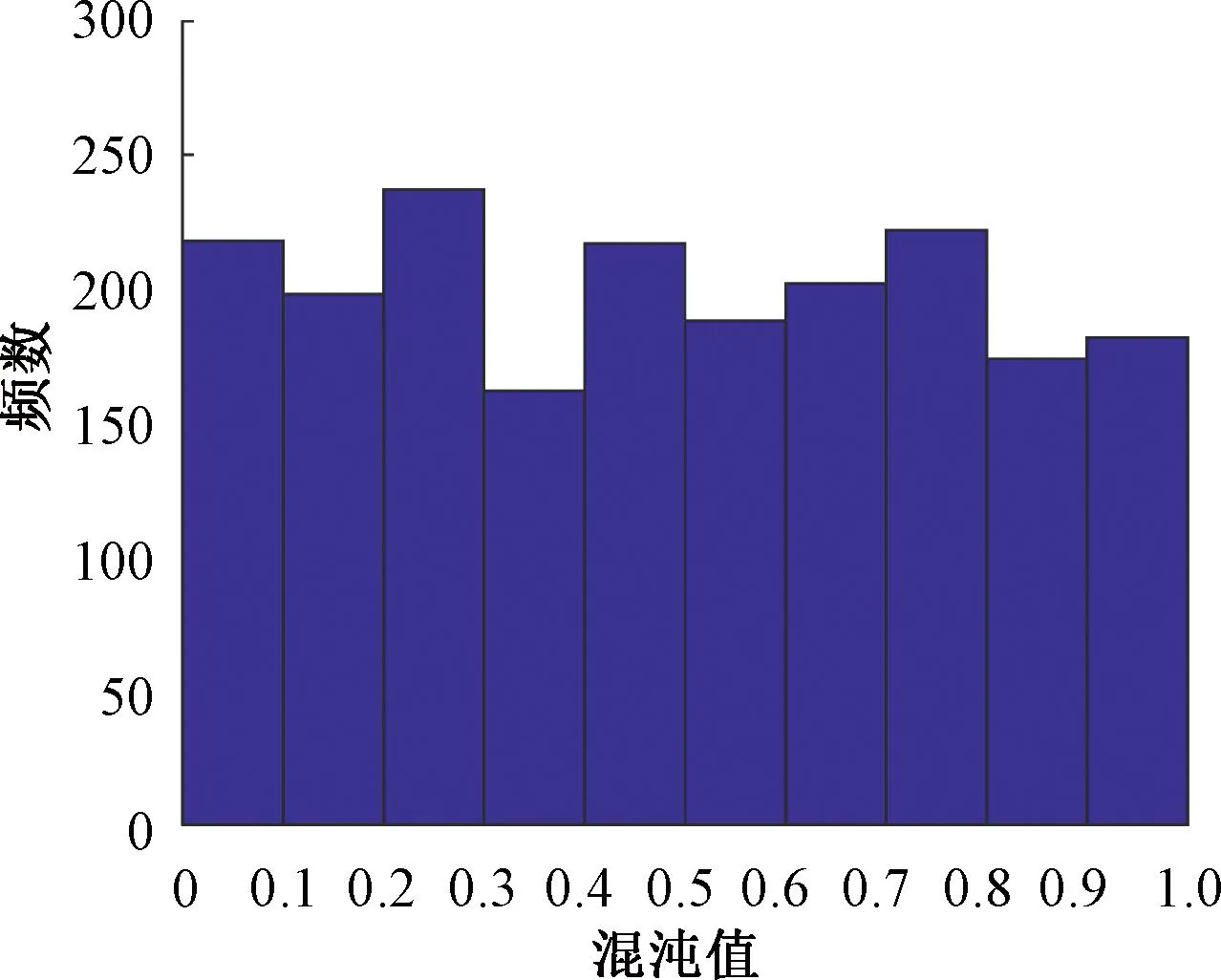
式中:t为当前迭代次数;Iiter,max为最大迭代次数;α为区间(0, 1]的随机数;Q为服从正态分布的随机数;L为1×h维矩阵,各元素均为1;R2为取值在0～1的预警值;SN为取值在0.5～1的安全值。当R2

跟随者位置更新为

(11)

式中:Yw为全局最差位置;Yp为全局最优位置;A为各元素随机赋值为1或-1的1×h维矩阵,且满足A+=AT(AAT)-1;n为解的维度。当e>n/2时,表明第e个跟随者未搜索到食物,存活率较低,需要前往其他区域搜寻食物,以提高自身适应度。

侦查者位置更新为

(12)

式中:Yg为当前全局最优位置;β为步长调整参数,取服从均值为0、方差为1的正态分布随机数;B为麻雀移动方位,取-1～1的随机数;fw、fg、fe分别为当前全局最差适应度、全局最优适应度、当前麻雀的适应度;σ为一个避免分母为0的极小常数。当fe≠fg时,表示该麻雀在种群的边缘带活动,易被捕食者发现而受到袭击;当fe=fg时,表示该麻雀位于种群的中心位置,且已察觉到被袭击的危险,需要迅速向其他区域的麻雀靠拢。

3.2 改进Circle混沌映射初始化种群

为增强初始种群的随机性、遍历性,提高算法的全局搜索能力,通常选择混沌映射初始化策略代替SSA算法中随机生成种群的方法以保持种群的多样性。常见的混沌映射有Circle混沌映射、Logistic映射和Tent混沌映射。本文选取比较稳定且混沌值的覆盖率较高的Circle混沌映射,其映射分布直方图见图3,映射关系为

图3 Circle混沌映射分布直方图

(13)

式中:ys为第s次迭代的Circle混沌序列。

由图3可见,Circle混沌值在区间[0.2, 0.6]上分布不均匀。文献 [20]将Circle混沌映射公式进行了改进,改进后的映射公式为

(14)

为直观清晰地显示改进效果,s取2 000。改进Circle混沌映射分布直方图见图4。

图4 改进Circle混沌映射分布直方图

3.3 自适应t分布策略

针对SSA算法后期种群多样性减少的问题,通过自适应t分布增强麻雀种群的多样性,对麻雀位置进行更新,避免算法陷入局部最优[21]。更新后的麻雀位置为

Ynew=Ye+Ye·t(Iiter)

(15)

式中:Ynew为改进后第e只麻雀的位置;Ye为改进前第e只麻雀的位置;t(Iiter)为以迭代次数为参数自由度的t分布。定义t分布变异概率为p,当满足α

3.4 改进SSA优化SVM的道岔故障诊断流程

改进SSA优化SVM的道岔故障诊断流程见图5,步骤如下:

图5 改进SSA优化SVM的道岔故障诊断流程

Step1从CSM系统中获取道岔正常转换及典型故障转换功率曲线数据,提取其时域、频域特征指标及小波包能量熵,组成特征指标向量。

Step2采用MDS方法对高维特征数据降维,降维后的维度需结合r值的变化趋势以及改进SSA-SVM道岔故障诊断模型的准确率确定。

Step3改进SSA算法。首先预设改进SSA的参数,利用改进Circle混沌映射初始化种群;其次通过计算个体适应度值,更新发现者、跟随者、侦查者的位置,确定当前种群的最优个体,判断当满足α

Step4实现SVM二分类向多分类的转换。其主要思想是采用Libsvm中的多分类,即一对一法,在q分类的情况下,任意2个类型训练出一个分类器,共训练出q(q-1)/2个分类器。当对一个未知样本进行分类时,根据q(q-1)/2个分类器的结果,采用投票方法给出得票最多的类别即为样本的故障类型。输入最佳参数X(bestc,bestg)及训练样本,构建改进SSA-SVM故障诊断模型。

Step5输入测试样本,分析道岔故障诊断结果。

4 道岔故障诊断模型构建及结果分析

4.1 道岔功率曲线样本建立

以某高铁车站ZDJ9型电动转辙机驱动的道岔为研究对象,根据道岔正常转换功率曲线F0及7种典型故障转换功率曲线F1～F7的各自不同特点,在CSM系统中选取344条道岔功率曲线,其中,F0、F5型各50条,F1型44条,其余各型均为40条;截取曲线6.4 s之前的部分,按40 ms的时间间隔采样,解锁阶段、转换阶段、锁闭阶段分别采集15、96、49个数据点,最终建立344×160维的道岔功率曲线样本。

4.2 多域道岔特征指标提取

1)时域特征指标。分别计算344组道岔功率曲线样本对应的5个区段的15个时域特征指标并做初步分析,发现解锁阶段的“最小值”均为0 W,“峰峰值”的大小与最大值重复,对故障识别没有实际意义,故删除以上2个时域指标;而对于F5型故障,其解锁“尖峰”功率低于正常值,需要增加“尖峰与0.32 s处功率值之差”,以量化该类型故障特征。综上,组成74维时域特征指标向量。

2)频域特征指标。分别对344组道岔功率曲线样本对应的5个区段的样本数据进行FFT变换,提取各段频谱的13个频域特征指标,组成65维频域特征指标向量。

3)小波包能量熵特征指标。在计算道岔功率曲线数据的小波包能量熵时,首先需要确定小波包分解层数K与小波基。其中K值影响着提取道岔故障特征指标的能力以及特征指标向量维数的高低,若K值过低,无法全面提取道岔故障信息,影响故障诊断的准确度;而若K值过高,导致提取的特征指标向量维数太高,影响故障诊断的速度以及准确度。常用的选取小波包最佳层数的计算式[22]为

(16)

式中:fs为采样频率;f为信号频率。根据道岔功率曲线的特点,取fs=25 Hz,f=0.156 Hz,得到k的最大整数值为5,即小波包的层数K取5。

在故障特征提取领域,通常采用Daubechies小波(dbM)作为小波基,其中M为小波阶数。分别将小波基的小波阶数M设置为0～10,当小波包分解层数为5层时,特征向量维数为32,则采用不同小波基时32个节点的小波包能量熵见图6。

图6 不同小波基下32个节点的小波包能量熵

图6表明,当选取db7进行分解后,各个节点上得到的能量熵差距最大,因此,小波基确定为db7。分别对344×160维道岔功率曲线样本数据进行5层小波包分解,得到32个小波包信号;对32个小波包信号进行重构,计算各重构信号的小波能量熵,归一化后组成32维小波包能量熵特征指标向量。

4.3 基于MDS的道岔特征指标降维

通过计算道岔功率曲线数据的多域特征指标,最终建立344×171维的道岔特征指标样本数据库;设定不同的特征指标维度参数,利用MDS方法对该样本进行降维,得到新特征指标,并根据式( 8 )计算不同维度对应的r值,评价函数值随维度的变化趋势见图7。

图7 评价函数值变化趋势

由图7可见,降维后的维度从1到20对应的r值依次减小,r值越小,表明降维后所包含的道岔功率曲线的特征信息量越大。其中,当降维至2维时,r值为0.111 1;8维时r值为0.022 6,表明已经能够较好地表征样本特征;而13维时r值为0.009 8。以降维至8维为例,降维前171维样本间欧氏距离、降维后8维样本间欧氏距离以及降维前后样本间欧氏距离偏差见图8。由图8(c)可见,其欧氏距离偏差在0.2的范围内,表明降维后8维数据特征可以最大限度地包含降维前171维数据特征。

图8 降维前后样本欧氏距离及偏差

在Matlab中编写改进SSA优化SVM中参数c、g的程序,并初始化相关参数,其中最大迭代次数设为100,麻雀数量为30,交叉验证折数为5,安全阈值为0.6,发现者的比例为0.7,侦察者的比例为0.2,t分布变异概率p为0.5[19],为减少参数寻优的进化次数,并提高故障诊断准确率,将c、g的优化范围设置为[10-5, 103]。选取不同道岔故障类型的后10组样本组成80组测试样本,其余的样本组成264组训练样本;采用改进SSA优化SVM算法的道岔故障诊断模型对不同维度的道岔故障样本数据进行故障诊断,诊断正确率见图9。

图9 不同维度的故障诊断正确率

图9表明,在采用改进SSA优化SVM算法时,随着特征指标维度的增加,样本数据包含的故障特征贡献率增大,当维度为8维时,故障诊断正确率首次达到最高,即为96.25%,故在满足降维效果的同时最大限度地包含故障特征,同时结合图7中的评价函数变化趋势,最终确定降维维度为8维。输入264×8维训练样本,对改进SSA算法参数寻优,其适应度曲线见图10。由图10可见,当进化代数为37次时,得到最佳参数组合为X(2.502 7, 0.971 3),最佳适应度fg为96.25%。

图10 适应度曲线

4.4 特征提取和降维的实验分析

分别输入344×74维时域特征指标样本(第1种)、344×65维频域特征指标样本(第2种)、344×32维小波包能量熵特征指标样本(第3种)、344×171维多域特征指标样本(第4种)、经MDS降维后的344×8维特征指标样本(第5种),以及经KPCA降维后的344×8维(第6种)、344×13维特征指标样本(第7种),以各种样本的264组样本数据为训练样本,训练改进SSA模型得到最佳X(bestc,bestg)参数组合,输入各种样本的80组测试样本和最佳优化参数至SVM故障诊断模型,得到以上7种样本的诊断结果,见表2。

表2 7种样本的诊断结果

由表2可以得出:

1)第1种时域特征指标样本的诊断准确率为93.75%,高于第2、3种样本,第1、2、3种样本的诊断结果见图11。由图11(b)可知,第2种频域特征指标样本对样本18较为敏感;由图11(c)可知,第3种小波包能量熵特征指标可以正确识别出样本46。将时域、频域和小波包能量熵3方面提取的特征指标组成第4种171维多域特征指标样本后,其故障诊断准确率均高于仅仅采用时域特征指标样本、频域特征指标样本或者小波包能量熵特征指标样本,从而验证了提取道岔多域特征指标可以提高故障诊断准确率和精确率。

图11 第1、2、3种样本的诊断结果

2)对比第4种与第5种样本对应的诊断准确率,显然,将171维的特征指标样本经MDS降维至8维后,不仅故障诊断准确率较高,而且模型训练时间最短。

3)为对比KPCA方法和MDS方法的降维效果,采用KPCA方法将344×171维的特征指标降维至不同的维度,训练并测试改进SSA-SVM模型,选择出准确率达到最大时的最低维度,即13维,对应诊断结果为表2中的第7种样本。对比第5、6、7种样本对应的准确率以及模型训练时间,当降维至8维时,MDS方法对应的准确率高于KPCA方法;而当KPCA降维至13维时,虽然其诊断准确率达到最大的95%,但是经过特征提取后维度依然较高,而且维数增多的同时也加长了模型训练时间。因此,MDS方法对本文数据的降维效果明显优于KPCA方法。

综上,提取道岔多域特征指标可以全面反映道岔故障特点;通过MDS方法降维,不仅提高了模型故障诊断的准确率、精确率和召回率,而且降低了模型训练时间,提高了故障诊断的实时性。

4.5 道岔故障诊断算法的实验分析

1)将80×8维的测试样本及最优参数X(2.502 7, 0.971 3)输入至SVM模型中,其诊断结果见图12。由图12可见,故障诊断准确率为96.25%,仅有F1型故障状态的样本91、93、94均错误诊断为F0型正常状态。

图12 8维测试样本的诊断结果

调取样本91、93、94的道岔转换功率曲线,该3条曲线均在道岔由反位向定位转换过程中,大概4.2 s处出现了小“鼓包”;而F1型故障的训练样本和其他测试样本均为道岔由定位向反位转换过程的功率曲线,大概1.2 s处出现小“鼓包”,可见改进SSA-SVM模型对道岔由反位向定位转换过程中的故障无法识别。以样本93为例,道岔功率曲线见图13。

图13 样本93的道岔功率曲线

结合现场实际情况,道岔在转换阶段出现“鼓包”功率是道岔由反位到定位时密贴过紧造成的,导致翻车掉道等事故的可能性较大,需及时明确故障原因,检查道岔缺口,调整道岔的密贴。在以后的研究中,建立样本数据时,可以考虑道岔定反位转换过程,以解决该问题。

2)分别建立基于GA、GWO、PSO、SSA等智能优化算法优化SVM算法的道岔故障诊断模型,并设置和改进SSA-SVM模型相同的最大迭代次数和种群数量,输入264×8维的训练样本训练各模型,输入80×8维的测试样本,其诊断结果见表3。表3结果表明:采用改进SSA-SVM模型较其他4种模型具有较高的故障诊断准确率、精确率、召回率,以及最短的训练时间;SSA-SVM模型将F7型的故障样本10错误诊断为F3型故障,而改进SSA-SVM模型对F7型故障诊断率达到100%,从而进一步验证了改进SSA-SVM算法具有良好的寻优性能。

表3 5种优化算法的测试诊断结果

3)对比文献 [6-8]中方法,道岔故障诊断准确率见表4。由表4可见,本文提出的MDS-改进SSA-SVM模型具有较高的故障诊断准确率;从是否能够完全正确识别出故障种类而言,仅F1型故障诊断准确率未达到100%,该问题可以进一步通过完善样本解决。综上,本文所提方法具有一定的优势。

5 结论

1)本文分别提取道岔功率曲线的时域、频域特征指标以及小波包能量熵,组成多域特征指标向量,能够更加全面地反映出道岔的故障特点。

2)利用MDS方法对所提取的原始特征指标进行降维优化,得到新的特征指标数据,可以较好地表征原始特征指标数据包含的信息,提高道岔故障诊断的准确率和实时性,降维效果明显优于KPCA方法。

3)改进SSA算法中采用改进Circle混沌映射初始化种群增加了种群的均匀性,自适应t分布策略增强SSA算法的种群多样性;采用改进SSA算法优化SVM中的参数c和g,避免了因人为经验选取参数产生误差。故障诊断结果表明,改进SSA算法具有良好的寻优能力,提高了故障诊断准确率。

4)通过实验分析以及与其他方法的故障诊断准确率进行对比,改进SSA-SVM的道岔故障诊断模型诊断准确率高达96.25%,不仅可以为道岔故障维修提供理论依据,而且实现了道岔的“压缩故障延时”,能够满足铁路现场维护需求。