考虑局部损伤区变化的能量平衡尺寸效应模型1)

刘小宇 张慧梅,2) 杨 政

* (西安科技大学理学院,西安 710600)

† (西安交通大学人居环境与建筑工程学院,西安 710049)

引言

不同于理想脆性材料在突然破坏之前的变形没有明显的损伤过程,实际材料,例如岩石、混凝土、聚合物、合金和复合材料等内部含有大量缺陷 (裂纹、空洞、位错、夹杂和晶界等),在达到极限载荷前一直存在缺陷的萌生、发展和聚合,这类材料被称为准脆性材料[1].准确描述混凝土、岩石等准脆性材料单轴抗压强度的尺寸效应对宏微观结构的安全设计和制造至关重要[2-3].准脆性材料的单轴抗压强度通常表现为“越小越强”,即下降尺寸效应[4-5].然而,当试件尺寸小于某一临界值时,大量的试验和模拟结果表明: 单轴抗压强度呈现上升尺寸效应,即试件尺寸越小,准脆性材料单轴抗压强度越低[6-18],在纳米金属和纳米合金中也观察到类似的上升尺寸效应现象[19-20].因此,随着试件尺寸的减小,准脆性材料单轴抗压强度先增大后减小.这意味着准脆性材料在特定尺寸下可以实现最大单轴抗压强度,实现结构的最优尺寸[21];但是这也意味着传统的“越小越强”设计思想对于小尺寸准脆性材料结构不再适用[4,22].目前,如何解释和预测单轴抗压强度从下降到上升尺寸效应转变一直是力学和材料研究的前沿问题[23-24].

对于下降尺寸效应,Weibull 基于最弱链理论建立统计尺寸效应理论.最弱链理论假设一个试件由N个独立的链组成,一旦最薄弱链发生破坏,试件就没有前兆现象地突然破坏.此后,研究者还提出其他类型的统计尺寸效应模型描述平均强度及其波动[25-27].然而,统计尺寸效应模型忽略了断裂过程区引发的确定性尺寸效应.为了体现抗拉强度的确定性尺寸效应,Bažant 等[28-30]考虑断裂过程区和能量释放平衡建立了缺口结构和非缺口结构的尺寸效应定律(size effect law,SEL).通过分析材料破坏面的几何相似性,Carpinteri 等[31-33]建立了多重分形尺寸效应模型(multifractal scaling law,MFSL).事实上,当准脆性材料试件达到极限强度时,断裂过程区越大,破坏面的分形就会越复杂,这意味着SEL 和MFSL 背后的机理相同.Hu 等[34]提出边界尺寸效应模型(boundary effect model,BEM) 来解释下降尺寸效应.Guan等[35-37]考虑最大骨料或晶粒尺寸修正了BEM,使BEM能更为准确预测材料真实断裂韧性和拉伸强度.考虑断裂过程区尺寸随试件尺寸变化,Ayatollahi等[38]基于最大周向应力准则建立一个新尺寸效应模型,以下简称AAM.Cornetti 等[39]和Leguillon 等[40]结合应力和能量准则提出有限断裂力学(finite fracture mechanics,FFM),FFM 可以同时确定强度和断裂过程区的尺寸效应.Bažant 等[41]、Di 等[42]和Chen等[43]也通过结合统计和确定性尺寸效应机理建立联合尺寸效应模型.Bažant 等[44]认为单轴压缩破坏时轴向或倾斜裂缝屈曲释放的能量等于劈裂裂缝所消耗的能量,并建立了相应的单轴抗压强度的尺寸效应模型,以下简称BXM 模型.Weiss 等[45]认为压缩破坏是从完好状态到失效状态的临界相变,并推导出平均抗压强度与其标准差的有限尺寸效应定律(fractal fracture size-effect law,FFSEL).FFSEL 可以预测尺寸趋于无穷大时单轴抗压强度趋于常数.研究者也提出许多经验模型来描述强度的下降尺寸效应[46-49].由于经验模型简单且准确,使其在工程中广泛应用.笔者通过分析准脆性材料单轴压缩试件变形破坏过程中的能量输入、储存和耗散,建立能反映单轴压缩破坏机理的能量平衡尺寸效应模型[50].

然而,准脆性材料的单轴压缩破坏是由微/细观缺陷的萌生、扩展和聚合引起[51-55],基于最弱链理论的统计尺寸效应模型不能体现这一机理.此外,SEL,BEM,AAM,FFM 和联合尺寸效应模型假设准脆性材料的破坏是拉应力驱动,不能反映压应力和沿裂纹表面摩擦对拉裂纹的抑制作用.准脆性材料压缩破坏也不是BXM 模型假设的裂纹屈曲,并且BXM 模型也不能预测尺寸趋于无穷大时单轴抗压强度趋于常数.FFSEL 模型物理机制过于复杂且难以理解.经验模型是对试验数据规律的拟合,难以反映准脆性材料单轴压缩破坏的机理.显然,上述下降尺寸效应模型难以体现单轴抗压强度的上升尺寸效应.

对于上升尺寸效应,考虑试件表面的强度和弹性模量较弱,Andrianopoulos 等[56]建立基于应变能密度准则的上升尺寸效应模型,但是该模型无法体现准脆性材料抗压强度从下降到上升尺寸效应的转变.考虑断裂韧性的分形特征,Bažant[57]提出分形断裂尺寸效应定律,当断裂韧性分形维数大于1 时,FFSEL 可以描述强度的上升尺寸效应.Masoumi 等[4]观察到抛光表面试件的单轴抗压强度增加,但上升尺寸效应区域的单轴抗压强度仍小于其最大值.因此,他们认为分形是引发单轴抗压强度上升尺寸效应的主要因素,表面缺陷可能是次要因素.在此基础上,结合FFSEL 和SEL,Masoumi 等[4]建立联合尺寸效应定律(unified size-effect law,USEL)来描述砂岩、石块和石灰岩由下降尺寸效应向上升尺寸效应转变.但是USEL 不能预测尺寸趋于无穷大时单轴抗压强度趋于常数,Masoumi 等[58]后来改进USEL(improved unified size-effect law,IUSEL)弥补这一不足,并用IUSEL 描述石灰石和人造石由下降尺寸效应向上升尺寸效应转变.然而,Bažant[57]指出裂纹表面的分形特征不可能是上升尺寸效应区域的主要机理,这意味着USEL 和IUSEL 不能反映上升尺寸效应背后的机理.

关于单轴抗压强度上升尺寸效应机理,Hoskins等[59]认为小试件单轴抗压强度上升尺寸效应是由表面缺陷引起.Zhang 等[60]假设颗粒流模型中缺陷尺寸与模型尺寸成正比或固定,模拟结果显示单轴抗压强度呈现上升尺寸效应.单轴压缩颗粒流模拟也表明上升尺寸效应主要是由模型孔隙率降低和模型尺寸与颗粒比增大引起[61-62].此外,单轴压缩有限元模拟发现小试件会沿着单个缺陷快速滑动破坏,导致抗压强度降低[63-64].Faramarzi 等[14]发现单轴压缩混凝土粒度越小,单轴抗压强度的上升尺寸效应越明显.这是由于试件晶粒尺寸越小,破坏表面越光滑,越容易发生滑移破坏.Quinones 等[13]、伍法权等[9]和王兆运[65]在单轴压缩玄武岩、砂岩和花岗岩中观察到较小试件中萌生的裂纹可以迅速贯通试件.从上述分析可以得出,单轴压缩小试件强度较低的根源是: 其破坏时局部破坏区域(即断裂过程区或者局部损伤区)较小.这就意味着试件应力达到单轴抗压强度时,局部破坏区域尺寸随着试件尺寸变化,而不是SEL,BEM,BXM 和 FSEL 中的常数.在FFM[39-40]和AAM 中[38],研究者已经考虑断裂过程区的尺寸效应.然而,一方面FFM 和AAM 是针对准脆性材料的拉伸破坏建立,不能反映其单轴压缩破坏物理机理.另一方面,FFM 和AAM 也不能体现单轴抗压强度从下降到上升尺寸效应转变.因此,建立能描述和解释单轴压抗压强度从下降到上升尺寸效应转变仍然是一个挑战性的问题.

笔者通过分析准脆性材料单轴压缩试件变形破坏过程中的能量输入、储存和耗散,建立能反映单轴压缩破坏机理的能量平衡尺寸效应模型[50].然而,在能量平衡尺寸效应模型中局部损伤区为常数,这使得其不能体现单轴抗压强度从下降到上升尺寸效应转变.因此,本文首先通过系统深入分析局部损伤区随试件尺寸的变化规律,提出局部损伤区尺寸效应模型并验证.在此基础上,建立考虑局部损伤区变化的能量平衡尺寸效应模型.然后分析模型参数对考虑局部损伤区变化的能量平衡尺寸效应模型影响,以便全面深入理解这一模型.最后应用已有大量试验数据验证本文尺寸效应模型,阐明其优缺点.

1 局部损伤区尺寸效应模型

1.1 局部损伤区尺寸效应模型构建

在准脆性材料中,破坏通常始于微/细观裂纹,然后微/细观裂纹萌生、扩展和聚合形成断裂过程区(fracture process zone,FPZ),即局部损伤区(localized damage zone,LDZ).由于LDZ 中微/细观裂纹的萌生、扩展和聚合引起的应力重分布、能量释放和耗散直接影响准脆性材料的确定性尺寸效应[66].因此,必须确定LDZ 尺寸效应,以便准确预测准脆性材料单轴压抗压强度的尺寸效应.

最大主应力理论[67]、能量释放平衡[66]、CTOD函数[68]、边界效应模型[69]或材料微观结构[70-71]认为不同尺寸的准脆性材料试件的拉伸LDZ 尺寸为定值.然而,基于黏聚力模型[42]、有限断裂力学[39]和能量释放率准则[70]表明: 随着试件尺寸的增加,拉伸LDZ 尺寸逐渐增加最终趋于常数.同时试验和模拟结果也发现了相同的拉伸LDZ 尺寸效应规律[72-75].事实上,可以想象: 在尺寸特别大的试件中,名义应力达到抗压强度极限时,LDZ 尺寸绝对要远大于试验室小尺寸试件产生的LDZ 尺寸.在此基础上,Ayatollahi 等[38]以及Fakhimi 等[72]提出如下拉伸LDZ 尺寸效应模型

式中,r∞为无限大试件中LDZ 尺寸,hldz为材料常数.rldz(D)表示特定尺寸D试件中拉伸LDZ 的大小,其值可以通过视觉图像方法、声学方法和力学方法确定[76].视觉图像方法通过分析试样表面变形前后的图像,确定试样表面的位移和应变分布,将LDZ 定义为局部高应变或者位移突变区[77].在视觉图像方法中,由于数字图像相关(digital image correlation,DIC)能准确地测量全场位移/应变分布受到广泛应用[72-73].声学方法通过捕捉材料破坏产生的声波,进而确定材料中微裂纹产生位置,最后确定LDZ 尺寸[74,78].力学方法利用模拟方法或者压痕仪测量LDZ力学性能变化的边界,进而确定LDZ 尺寸[79-80].

对于单轴压缩试件,从试验或模拟结果图可以观察到: 随着试件尺寸的增加,压缩LDZ 尺寸逐渐增加[63-64,81-83].此外,Mayolle 等[84-85]发现地壳中总断裂带厚度随着断层位移的增加呈非线性增长,直到地壳运动的阈值厚度.这表明在非常大的结构中,压缩LDZ 的厚度是一个固定值.因此,在式(1)中引入指数k来体现压缩LDZrldz与试件尺寸D之间的非线性关系,并且考虑当D≤rldz,压缩LDZ 尺寸rldz充满试样,试样尺寸D等于压缩LDZ 尺寸rldz,则压缩LDZ 尺寸rldz表达式如下

式中,参数k控制rldz与D的非线性关系.图1 给出不同k值时rldz随D的变化曲线.可以看出k能显著影响rldz(D) 曲线的非线性上升阶段.随着k增加,达到r∞的临界尺寸逐渐减小.图2 为不同hldz值的rldz(D)变化曲线.可以观察到,hldz越小,rldz越大,材料塑性变形越明显;即hldz能反映试件的韧脆性.因此,hldz是一个与试件几何形状、应力状态和材料力学性能有关的参数.r∞和hldz可以通过拟合试验或模拟结果确定.在式(2)中,当k=0 时,LDZ 尺寸rldz=r∞/hldz为常数,这和尺寸效应定律(SEL)[28-30]、单轴抗压强度的尺寸效应模型(BXM)[44]和边界尺寸效应模型(BEM) 中对LDZ 尺寸的假设一致,这时LDZ 尺寸不随试样尺寸变化.然而,试验和模拟结果表明: 随着试件尺寸的增加,压缩LDZ 尺寸逐渐增加,并最终趋于定值[63-64,81-85].此外,需要说明的是,拉伸LDZ 尺寸效应模型式(1)和式(2) (改进的公式(1))分别基于拉伸和压缩LDZ 尺寸效应试验和模拟结果建立,这意味式(1)和(2)是经验性的,不具备任何物理机制.因此,用式(2)去描述单轴压缩LDZ 尺寸效应是合理的.

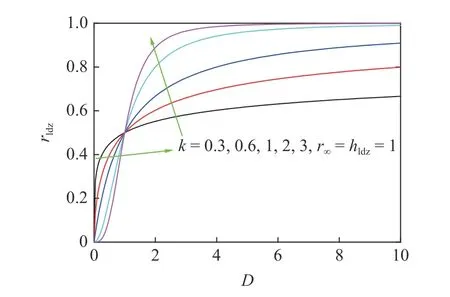
图1 参数k 对局部损伤区尺寸效应模型(式(2))影响Fig.1 Influence of parameter k on the size-dependent model of LDZ(Eq.(2))

图2 参数hldz 对局部损伤区尺寸效应模型(式(2))影响Fig.2 Influence of parameter hldz on the size-dependent model of LDZ(Eq.(2))

不同于上述拉伸破坏试件只有单个LDZ,单轴压缩试件通常可以观察到多个LDZ[76],这导致定量分析压缩LDZ 尺寸效应较难.由于声发射可以获取单轴压缩试件内部微裂纹萌生、扩展和聚合的特征,但是声发射定位时存在很高的误差,这使得单独使用声发射很难精确测量LDZ 尺寸.DIC 能准确测量试件表面全场位移/应变分布.Zhang 等[76,86-87]的研究表明: 结合声发射和DIC 方法可以准确测量压缩LDZ 尺寸.

1.2 局部损伤区尺寸效应模型验证

本节收集不同尺寸准脆性材料试件LDZ 尺寸的试验和模拟数据[73-74,79],并在表1 给出了试验和模拟材料类型、尺寸范围、LDZ 尺寸确定方法和数据来源.Tarokh 等[74]采用声发射(acoustic emission,AE)定位含裂纹三点弯曲试样所有微裂纹位置,认为所有微裂纹区的边缘为LDZ,并确定LDZ 长和宽随试件尺寸的变化规律.Zhang 等[73]基于DIC 计算含裂纹半圆形弯曲试样水平位移,将近似一条斜直线的水平位移梯度作为临界水平位移梯度,用来区分加载过程中LDZ 尖端与弹性区域;这条采样线所在位置与预制裂缝尖端的距离作为LDZ 的长度;水平位移曲线靠近裂尖时,水平位移梯度会出现突变点,以两点之间的距离作为LDZ 的宽度[88].开展不同尺寸含裂纹三点弯曲试样模拟时,文献[79-80]把LDZ 定义为单元已经进入软化阶段的区域.

表1 不同准脆性材料试件LDZ 尺寸试验和模拟数据Table 1 Experiment and simulated data of LDZ sizes for different quasi-brittle materials

对表1 中每组试验或者模拟数据,采用拟合方法确定式(1)和式(2)中参数k,r∞和hldz,在图3～图8 中给出.可以看出拟合确定的式(2)中k值差别较大(0.273 9～1.344),并且对于同一试验,LDZ 长度和宽度尺寸效应的非线性参数k也差别较大.这是因为: ①不同材料微观结构和力学特性不同;②不同试验试样几何形状不同;③沿长度和宽度方向LDZ 增大的机制不同;④试件的受力状态.这些因素综合作用使LDZ 尺寸效应非线性特征值k差别较大.

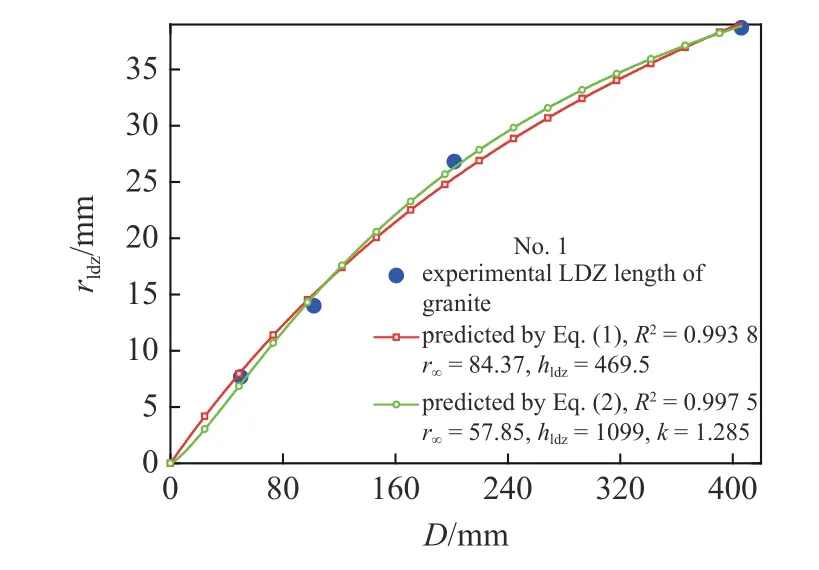
图3 式(1)和式(2)预测花岗岩试验LDZ 长度对比[74]Fig.3 Compared Eqs.(1) and (2) with experimental LDZ length of granite[74]

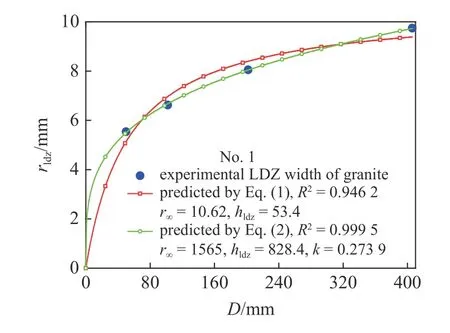
图4 式(1)和式(2)预测花岗岩试验LDZ 宽度对比[74]Fig.4 Compared Eqs.(1) and (2) with experimental LDZ width of granite[74]

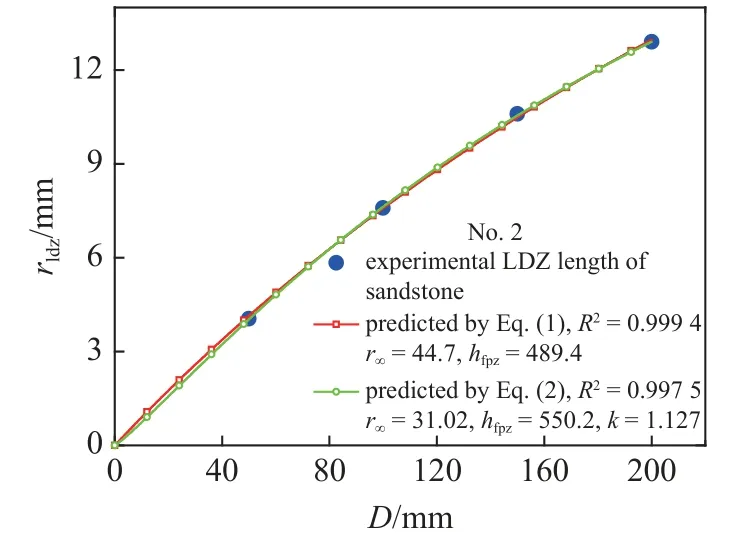
图5 式(1)和式(2)预测砂岩试验LDZ 长度对比[73]Fig.5 Compared Eqs.(1) and (2) with experimental LDZ length of sandstone[73]

图6 式(1)和式(2)预测砂岩试验LDZ 宽度对比[73]Fig.6 Compared Eqs.(1) and (2) with experimental LDZ width of sandstone[73]

图7 式(1)和式(2)预测混凝土模拟LDZ 长度对比[79]Fig.7 Compared Eqs.(1) and (2) with simulated LDZ length of concrete[79]

图8 式(1)和式(2)预测混凝土模拟LDZ 长度对比[80]Fig.8 Compared Eqs.(1) and (2) with simulated LDZ length of concrete[80]

把图3～图8 中参数k,r∞和hldz代入式(1)和式(2),式(1)和式(2)预测表1 中每组试验或者模拟数据的结果如图3～图8 所示.由图3～图8 可以看出式(1) 和式(2) 都能较好预测试验或者模拟rldz随D的变化规律,其确定系数R2都大于0.94.在图3～图8 中式(2) 拟合的每组数据的确定系数R2明显高于式(1)拟合的确定系数R2,这也就验证式(2)的正确性.

2 考虑局部损伤区变化的能量平衡尺寸效应模型

2.1 抗压强度能量平衡尺寸效应模型建立

通过分析图9 准脆性材料单轴压缩损伤力学模型变形破坏过程中的能量输入、储存和耗散,笔者在先前论文[50]中建立式(3)能反映单轴压缩破坏机理的能量平衡尺寸效应模型.不同于拉伸破坏试件只有单个LDZ,单轴压缩试件通常可以观察到多个LDZ[76],因此图9 中LDZ 为单轴压缩试件中多个LDZ 的综合

图9 准脆性材料单轴压缩损伤力学模型[50]Fig.9 Damage mechanics model of quasi-brittle material under uniaxial compression[50]

式中,n(n＞ 0)为体现名义损伤模量尺寸效应非线性的参数;σnm,fce和fc分别为单轴名义抗压强度、压缩弹性极限强度和真实抗压强度,且fce≤fc.V=πλD3/4 和VL=πabt/(4sinθ)分别为图9 中圆柱试样体积和LDZ 体积;D和H为单轴压缩圆柱试样直径和高,λ=H/D;a,b和t分别为椭圆状LDZ 的长轴、短轴和厚度,θ为LDZ 和试样水平方向夹角.事实上,当V≤VL,即πλD3/4 ≤ πabt/(4sinθ) ⇒D≤,LDZ 充满试样,试样体积等于LDZ 体积,这时单轴压缩试样名义应力应变曲线与真实应力应变曲线重合,名义抗压强度σnm等于真实抗压强度fc.

把V=πλD3/4 和VL=πabt/(4sinθ)代入式(3),并令体现图9 中单轴压缩试件中LDZ 尺寸,其量纲为长度,则可得

能量平衡尺寸效应模型(式(4))能反映名义抗压强度的下降尺寸效应,即随着试件尺寸D的增大,名义抗压强度σnm减小[4,5,89-90].然而,当D减小到特定尺寸以下时,试验和模拟结果表明: 随着D的减小,试件的抗压强度会逐渐减小,即名义抗压强度的上升尺寸效应[6-17].此外,由第1 节可以得出,LDZ尺寸rldz随着D的增加呈非线性增长,最终趋于定值[73-74,79-80].事实上,可以想象: 在特别大的试件尺寸中,名义应力达到抗压强度极限时,LDZ 绝对要远大于试验室小试件产生的LDZ.因此,将式(2)代入式(4),可得名义抗压强度σnm表达式如下

式中右侧rldz参见式(2).

2.2 抗压强度能量平衡尺寸效应模型参数研究

为了研究参数对考虑局部损伤区变化的能量平衡尺寸效应模型的影响,对式(5)进行整理可得

式中,α=fce/fc,0 ≤α≤ 1.下面通过研究参数对考虑局部损伤区变化的能量平衡尺寸效应模型变化规律的影响,以便全面深入理解这一模型.

图10～图14 给出了参数α,n,r∞,hldz和k对考虑局部损伤区变化的能量平衡尺寸效应模型影响.通过对图10～图14 进行全面分析,可以得出如下5 种类型的尺寸效应曲线.

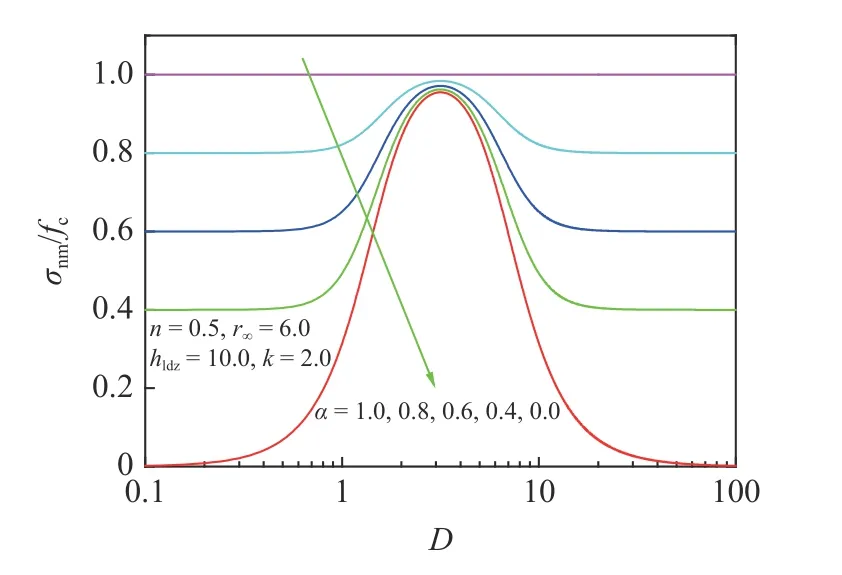
图10 参数α 对本文模型影响Fig.10 Effect of the parameter α on the proposed model

类型1: 在图14 中k=1 时,可以看出,随着尺寸D增大,σnm/fc逐渐减小,最终趋于α,这和大量单轴压缩试验与模拟结果一致[50,91-92].需要说明的是,类型1 没有平直段(即σnm/fc不随尺寸变化)的原因是: 对于任何尺寸试件,局部损伤区的尺寸rldz一直小于试件尺寸,即处于式(6)中D＞rldz范围.

类型2: 在图14 中k=0 时,可以看出,随着尺寸D增大,σnm/fc首先在一定尺寸范围内保持为常数1,然后逐渐减小,最终趋于α.Chen 等[93]发现单轴压缩光刻加工硅的剪切强度尺寸效应具有同样的规律,并发现小尺寸试样剪切滑移带呈现充满试样且均匀分布.即式(6)中,当D≤rldz,损伤区充满试样,试样体积等于损伤区尺寸,这时σnm/fc=1.

类型3: 可以看出,在图10～图14 中有部分曲线,随着尺寸D增大,σnm/fc先增加,然后逐渐减小,最终趋于α.研究者在砂岩[11]、石灰石[8]、人造石膏[8]、混凝土[14]、玄武岩和花岗岩[9,13,65]发现类型3 尺寸效应.单轴压缩有限元模拟发现小试件会沿着单个缺陷快速滑动破坏,导致抗压强度呈现类型3 升尺寸效应[63-64].Faramarzi 等[14]发现单轴压缩混凝土粒度越小,单轴抗压强度的上升尺寸效应越明显.这是由于试件晶粒尺寸越小,破坏表面越光滑,越容易发生滑移破坏.文献[9,13,65]在单轴压缩玄武岩、砂岩和花岗岩中观察到较小试件中萌生的裂纹可以迅速贯通试件.从上述分析可以得出,单轴压缩小试件强度呈现上升尺寸效应的原因是其破坏时LDZ较小.

类型4: 从图12 中r∞=10.0,8.0 以及图14中k=4,可以看出,随着尺寸D增大,σnm/fc先逐渐增加到1,然后在一定尺寸范围保持常数1,再逐渐减小,最终趋于α.类型4 尺寸效应是本文理论模型发现之后,通过查阅大量文献,在微纳尺度钛合金尺寸效应试验数据中证实这一规律[94].Quek 等[95]开展的纳米金属晶粒尺寸效应离散位错动力学模拟结果也呈现类似规律.事实上,类型4 产生的原因是:式(6)中压缩LDZ 尺寸rldz具有3 段,即随着试件尺寸D增大,压缩LDZ 尺寸rldz首先增大(处在D＞rldz范围),然后尺寸rldz=D(处在D≤rldz范围),最后rldz再增大并逐渐趋于定值r∞(处在D＞rldz范围).

类型5: 在图10 中α=1.0、图11 中n=0.0 和图12 中r∞=0.0 可以看出σnm/fc无尺寸效应.然而,图10 中α=1.0 和图11 中n=0.0 与图12 中r∞=0.0 名义抗压强度无尺寸效应的机理并不相同.图10中α=1.0 和图11 中n=0.0 损伤区充满整个试件,图12 中r∞=0.0 时局部损伤区尺寸rldz=0,试件为完全脆性破坏.高强和纤维增强混凝土单轴抗压强度不随试样尺寸变化,并观察到试样呈现处整体性破坏,即就是损伤区充满整个试件[96-97].由于完全脆性破坏是理想化的,因此,并未查阅到理想化脆性破坏(rldz=0)呈现的无尺寸效应现象.

图11 参数n 对本文模型影响Fig.11 Effect of the parameter n on the proposed model

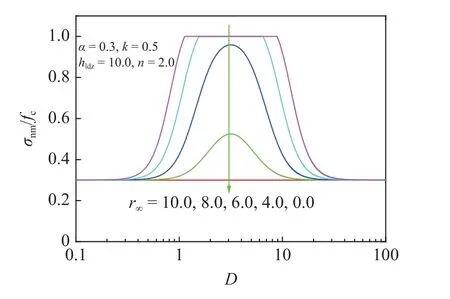
图12 参数r∞ 对本文模型影响Fig.12 Effect of the parameter r∞ on the proposed model

在图10 和图11 中,α=fce/fc表示抗压弹性极限强度和真实抗压强度比值,参数n可以调整名义损伤模量尺寸效应的非线性.随着α从0 增大到1 或n逐渐减小到0,(σnm/fc)−D曲线整体增大,最终σnm/fc无尺寸效应.这是因为当α从0 增大到1或n逐渐减小到0 时,名义损伤模量En和真实损伤模量Ed逐渐接近并相等,名义应力应变曲线与真实应力应变曲线逐渐接近并重合,最终整个试件会同时破坏,导致名义抗压强度σnm等于真实抗压强度fc.

在图12 和图13 中,r∞为无限大试件中LDZ 尺寸,hldz反映材料的韧脆性.当r∞逐渐减小到0 或者hldz逐渐增大时,本文模型的尺寸效应逐渐减弱.这是因为当r∞逐渐减小或者hldz逐渐增大时,试样中局部损伤区尺寸rldz逐渐减小,试件最终接近完全脆性破坏.

指数k可以调整压缩局部损伤区rldz与试件尺寸D之间关系的非线性,从图14 可以看出,随着k逐渐减小,本文模型的尺寸效应先减弱然后增强,并且先从类型4 转变为类型3,再转变为类型1,最后转变为类型2.

图14 参数k 对本文模型影响Fig.14 Effect of the parameter k on the proposed model

下面进一步阐明各种类型名义抗压强度σnm尺寸效应的原因.把式(6)整理为如下形式

上式对尺寸D求导可得

式中,rldz′/rldz和D′/D分别是rldz和D随D变化的相对变化率.

对式(2)求导可得rfpz′/rfpz为

在式(8) 中,参数0 ≤α≤ 1;n,r∞,hldz,k≥0,且rldz≤D,因此,(σnm2/fc2)′正负由(rldz′/rldz−D′/D)控制.当(rldz′/rldz−D′/D)＞ 0,(σnm2/fc2)′＞ 0,σnm/fc随D增大而增大,呈现上升尺寸效应.当(rldz′/rldz−D′/D)＜ 0,(σnm2/fc2)′＜ 0,σnm/fc随D增大而减小,呈现下降尺寸效应.当(rldz′/rldz−D′/D) ≡ 0,(σnm2/fc2)′ ≡0,σnm/fc随D增大不变化,呈现无尺寸效应现象.这就意味rldz′/rldz和D′/D之间的竞争是本文尺寸效应模型(式(6))能体现5 种类型的尺寸效应的原因.

进一步由式(9)和式(10)可得到

式中,当k＜ 1 时,(rldz′/rldz−D′/D) ≤ 0,(σnm2/fc2)′＜0,则σnm/fc随D增大而减小.当k≥ 1 时,令(rldz′/rldz−D′/D)=0,可得式(6)极大值点对应的试件尺寸为D=[(k− 1)hldz]1/k.因此,随着D增大,(rldz′/rldz−D′/D) 由正转负最后趋于0,σnm/fc先增大后减小趋于常数.显然,进一步研究表明,式(6)变化规律主要受参数k和hldz控制.

3 考虑局部损伤区变化的能量平衡尺寸效应模型验证

3.1 验证数据收集

在本文提出的考虑局部损伤区变化的能量平衡尺寸效应模型(式(5))中令k=0 可得能量平衡尺寸效应模型(式(4)).笔者先前的论文[50]已经采用大量试验和模拟数据验证了能量平衡尺寸效应模型(式(4))预测类型1 和2 名义抗压强度尺寸效应[50].同时,由第2 节的图10 中α=1.0、图11中n=0.0 和图12 中r∞=0.0 可以看出,考虑局部损伤区变化的能量平衡尺寸效应模型能体现名义抗压强度无尺寸效应现象.因此,本文只收集类型3 和4 的尺寸效应试验数据对考虑局部损伤区变化的能量平衡尺寸效应模型进行验证,其中编号1～9 试验数据能体现类型3 尺寸效应现象,只有编号10 钛合金试验数据能体现类型4 尺寸效应现象.本文对准脆性材料的定义为: 材料内部含有大量缺陷 (裂纹、空洞、位错、夹杂和晶界等),在达到极限载荷前一直存在缺陷的萌生、发展和聚合,这类材料被称为准脆性材料[1].岩石、混凝土与合金材料破坏都萌生于缺陷引发的应力集中处,然后在应力集中处首先破坏并逐渐扩展、聚合.此外,岩石、混凝土与合金材料破坏时最终形成的LDZ 都是能量耗散和释放的通道.因此,用本文的考虑局部损伤区变化的能量平衡尺寸效应模型去描述岩石、混凝土与合金材料的尺寸效应是合理的.表2 给出了收集数据的材料类型、试件尺寸D范围、数据量和数据来源.考虑到试验数据的收集通常较为耗时耗力,笔者把表2 涉及的数据上传到百度网盘(https://pan.baidu.com/s/1eZai0IqdVaqHkISWpUe8Ow,密码: 1234),方便其他研究者在未来使用这些数据进行科学研究.

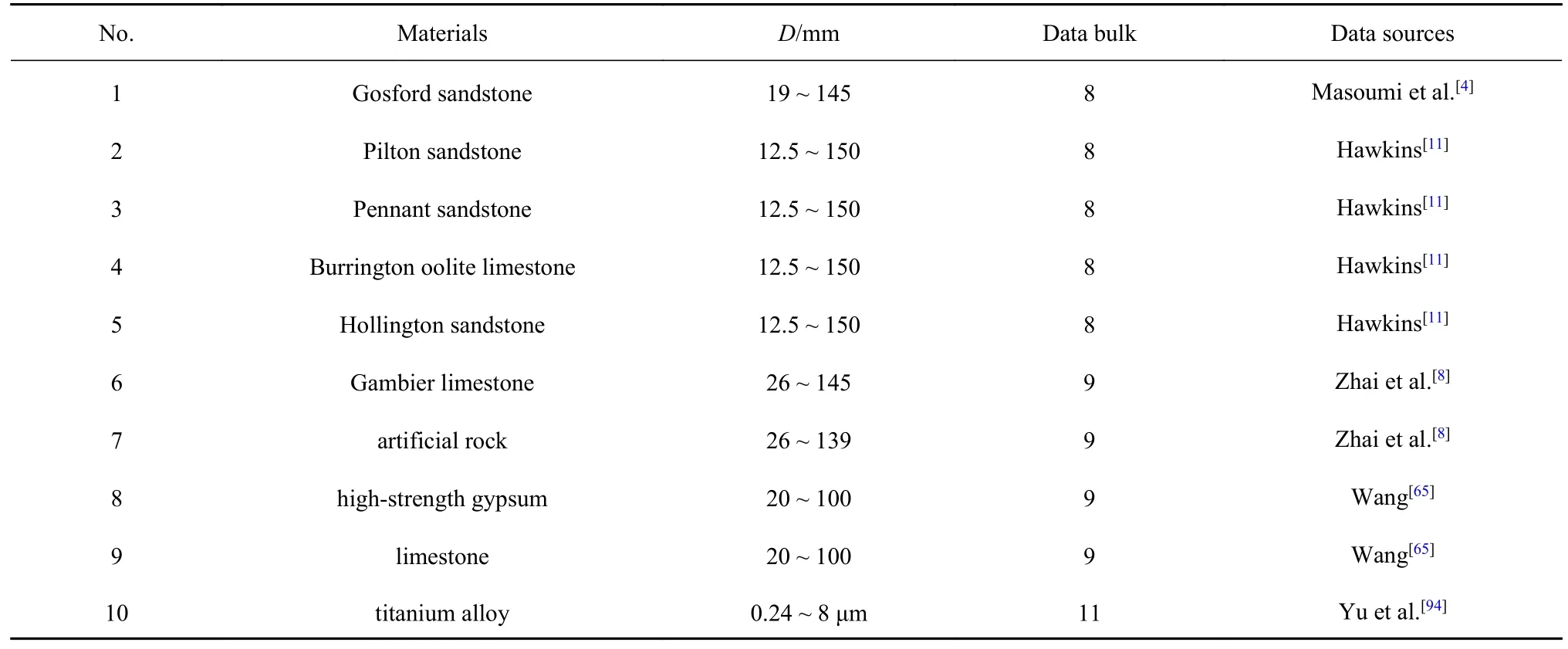
表2 不同材料抗压强度尺寸效应试验数据Table 2 Experimental data of size effect of compressive strength for different materials

3.2 模型验证及对比

对表2 中每组试验数据,采用非线性最小二乘方法拟合确定本文考虑局部损伤区变化的能量平衡尺寸效应模型(式(5)) 的6 个参数fce,fc,n,r∞,hldz和k,在表3 给出.此外,采用本文模型(式(5))拟合每组试验数据时,需要每个参数的初值和范围,初值越接近拟合值,拟合的准确性越高且用时约少.因为参数fce为试件尺寸趋于无穷大时的名义应力,这意味着参数fce小于或等于试验名义抗压强度最小值;而参数fc为真实抗压强度,其大于或等于试验名义抗压强度最大值.基于上述分析就可以很快确定参数fce和fc的初值和范围,进而可大幅提高拟合的效率.

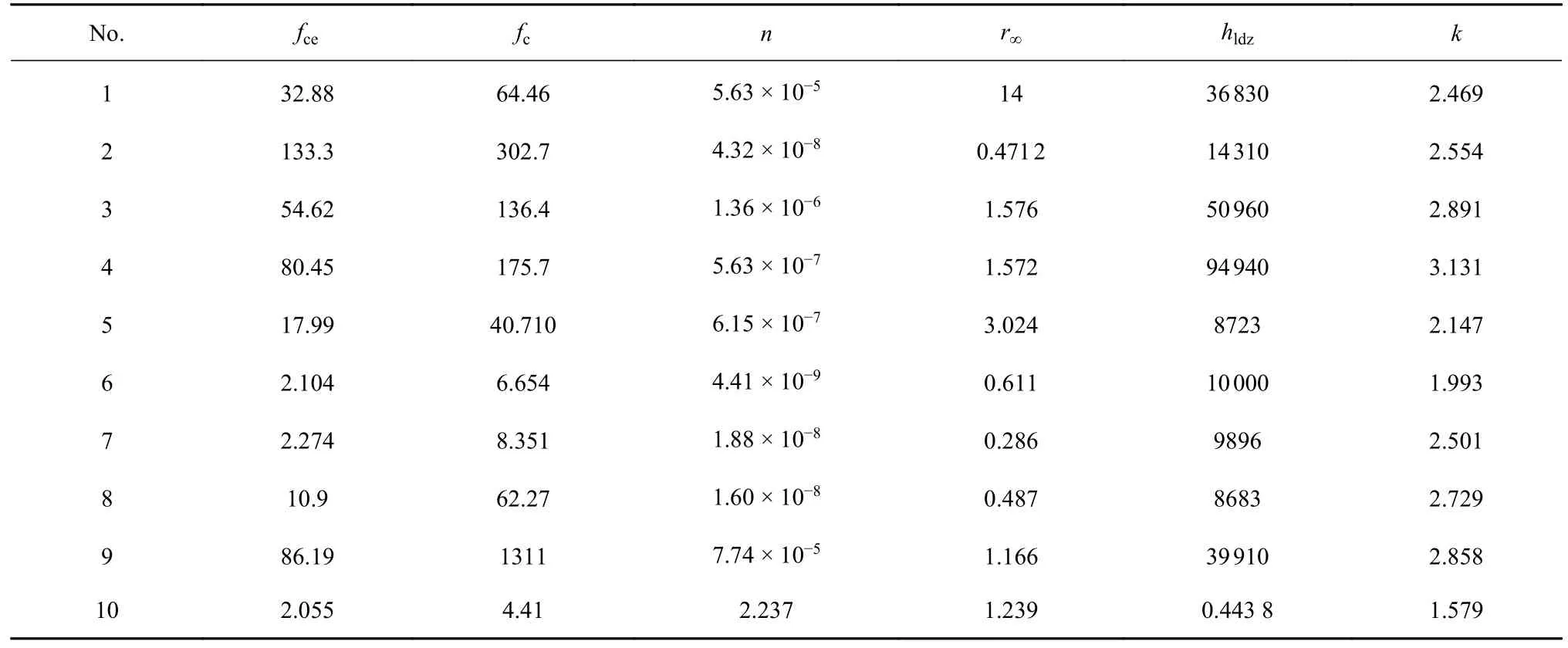
表3 不同材料的本文提出模型 (式(5))拟合参数值Table 3 The optimized parameters of the proposed model (Eq.(5)) for different materials

对于编号1～10 尺寸效应试验数据如表3 和图5～图24 所示,从表3 可以看出,除编号1 Gosford 砂岩数据拟合确定的r∞=14 mm 较大,其余编号2～9 数据拟合确定的r∞在0.286～3.024 mm 范围,Hu 等[69,98]认为LDZ 尺寸和晶粒大小在同一尺度,显然本文拟合确定的r∞范围和岩石晶粒大小在同一尺度.对编号10 数据拟合确定的试件尺寸趋于无穷大时LDZ 尺寸r∞=1.239 μm,显然r∞=1.239 μm 大于钛合金平直段向下降尺寸效应转变(图24)的LDZ 尺寸值0.7 μm,这就表明拟合确定的r∞较为合理.对比表3 中拟合确定的参数fce和fc值以及图15～图24中名义抗压强度值,可以看出fce小于或接近试验名义抗压强度最小值,而fc大于或接近试验名义抗压强度最大值.n,r∞,hldz和k都大于等于0.这就表明考虑局部损伤区变化的能量平衡尺寸效应模型拟合参数fce,fc,n,r∞和hldz,k处在预设范围内.对于编号1～9 类型3 尺寸效应试验数据,考虑局部损伤区变化的能量平衡尺寸效应模型拟合参数n接近0,n体现名义损伤模量尺寸效应非线性,这说明产生类型3 尺寸效应的主导因素是局部损伤区尺寸的变化,而非名义损伤模量随尺寸的非线性变化.

图15 两种尺寸效应模型预测编号1 Gosford 砂岩试验数据对比Fig.15 Comparison of experimental values and predicted results of two size effect models for No.1 Gosford sandstone

图16 两种尺寸效应模型预测编号1 Pilton 砂岩试验数据对比Fig.16 Comparison of experimental values and predicted results of two size effect models for No.2 Pilton sandstone

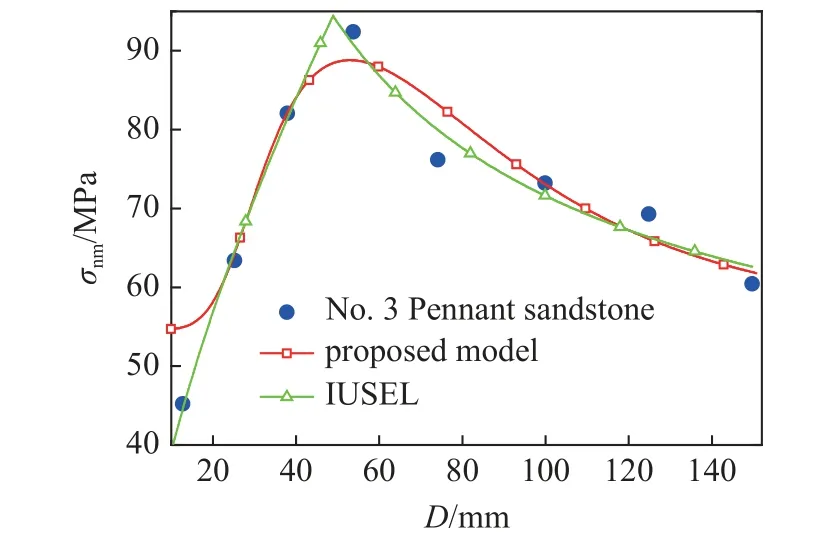
图17 两种尺寸效应模型预测编号3 Pennant 砂岩试验数据对比Fig.17 Comparison of experimental values and predicted results of two size effect models for No.3 Pennant sandstone

图18 两种尺寸效应模型预测编号4 Burrington oolite 砂岩试验数据对比Fig.18 Comparison of experimental values and predicted results of two size effect models for No.4 Burrington oolite limestone

图19 两种尺寸效应模型预测编号5 Hollington 砂岩试验数据对比Fig.19 Comparison of experimental values and predicted results of two size effect models for No.5 Hollington sandstone

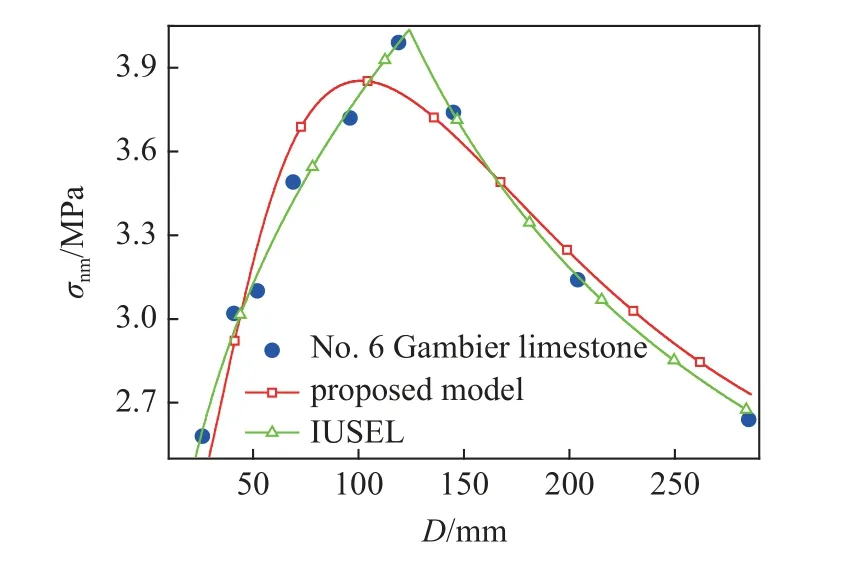
图20 两种尺寸效应模型预测编号6 Gambier 石灰石试验数据对比Fig.20 Comparison of experimental values and predicted results of two size effect models for No.6 Gambier limestone

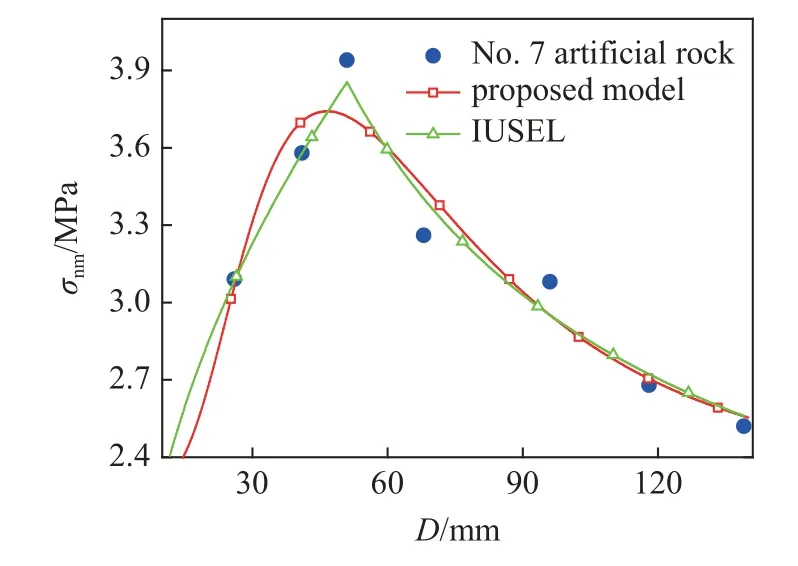
图21 两种尺寸效应模型预测编号7 人造岩石试验数据对比Fig.21 Comparison of experimental values and predicted results of two size effect models for No.7 artificial rock

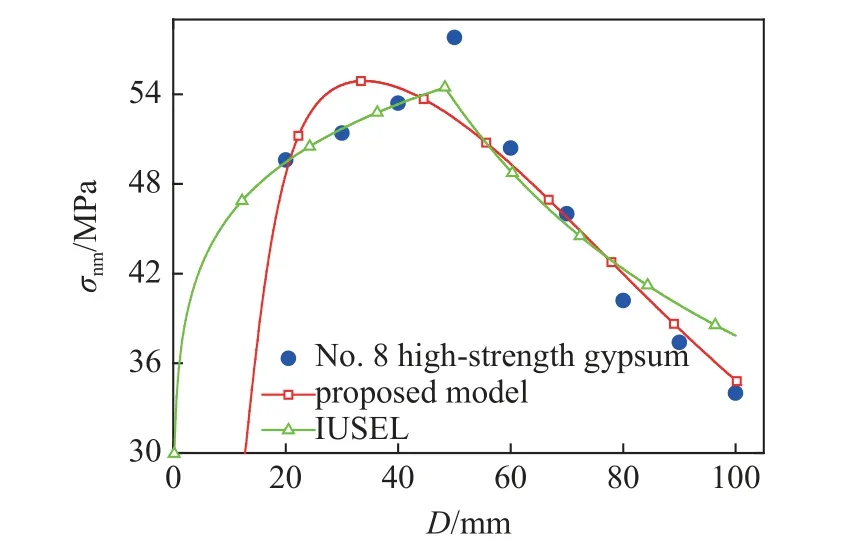
图22 两种尺寸效应模型预测编号8 高强石膏试验数据对比Fig.22 Comparison of experimental values and predicted results of two size effect models for No.8 high-strength gypsum

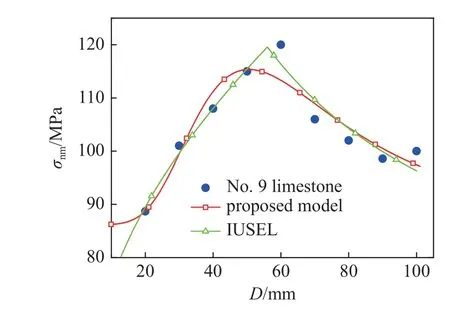
图23 两种尺寸效应模型预测编号9 石灰石试验数据对比Fig.23 Comparison of experimental values and predicted results of two size effect models for No.9 limestone

图24 两种尺寸效应模型预测编号10 钛合金试验数据对比Fig.24 Comparison of experimental values and predicted results of two size effect models for No.10 titanium alloy

由于能量平衡尺寸效应模型(式(4))不能体现类型3 和4 尺寸效应试验数据,因此,本文没有选择能量平衡尺寸效应模型进行对比研究,而选择如下改进的联合尺寸效应定律[8]和考虑局部损伤区变化的能量平衡尺寸效应模型进行对比研究.

式中,fm,Di,l和df为模型参数.对表1 中每组试验数据,采用和考虑局部损伤区变化的能量平衡尺寸效应模型(式(5))相同的拟合方法确定IUSEL (式(12))的参数见表4.

表4 不同材料的IUSEL (式(12))拟合参数值Table 4 The optimized parameters of the IUSEL (Eq.(12)) for different materials

把表3 和表4 中拟合参数分别代入考虑局部损伤区变化的能量平衡尺寸效应模型(式(5))和IUSEL(式(12)),这两种尺寸效应模型预测表2 中每组试验数据的结果如图15～图24 所示.对于编号1～9 类型3 尺寸效应试验数据,可以看出考虑局部损伤区变化的能量平衡尺寸效应模型和分段的IUSEL 预测结果差别不大.

从图24 可以看出IUSEL 不能体现编号10 类型4 尺寸效应数据变化规律.而考虑局部损伤区变化的能量平衡尺寸效应模型能很好预测编号10 类型4 尺寸效应数据变化规律.这是因为考虑局部损伤区变化的能量平衡尺寸效应模型能体现试件尺寸D≤rldz时,即LDZ 充满试样,试样体积等于LDZ 体积,这时单轴压缩试样名义应力应变曲线与真实应力应变曲线重合,名义抗压强度σnm等于真实抗压强度fc.同时,采用拟合方法确定式(5)中真实抗压强度fc为4.4 GPa,这与试验数据确定的fc=4.41 GPa 非常接近.这也证明本文提出的考虑局部损伤区变化的能量平衡尺寸效应模型的正确性.

为了定量对比考虑局部损伤区变化的能量平衡尺寸效应模型和分段的IUSEL 预测结果的准确性.计算两种模型预测结果的确定系数R2见表5.可以看出,考虑局部损伤区变化的能量平衡尺寸效应模型预测编号2,8 和10 尺寸效应数据R2最大,IUSEL预测编号1,3～7 和9 尺寸效应数据R2最大.进一步对比发现考虑局部损伤区变化的能量平衡尺寸效应模型和分段的IUSEL 预测所有尺寸效应数据结果的总平均确定系数M-R2接近,但是考虑局部损伤区变化的能量平衡尺寸效应模型能描述5 种不同类型的尺寸效应.

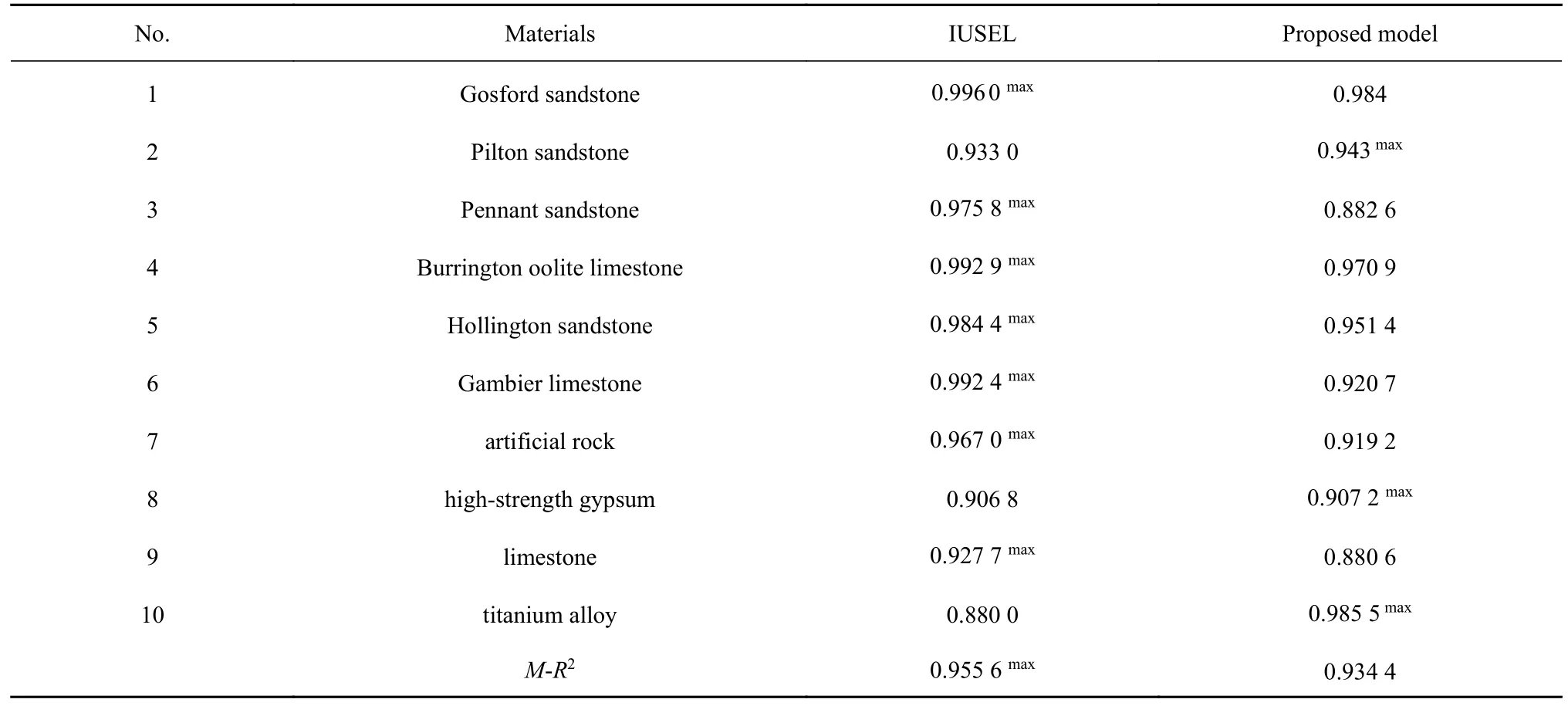
表5 IUSEL 和本文提出模型预测结果的确定系数R2 和总平均确定系数M-R2Table 5 The determination coefficients of the IUSEL and proposed model for different materials

4 结论

本文首先通过系统深入分析局部损伤区随试件尺寸的变化规律,提出局部损伤区(LDZ)尺寸效应模型.在此基础上,建立考虑局部损伤区随尺寸变化的能量平衡尺寸效应模型.然后分析参数对考虑局部损伤区变化的能量平衡尺寸效应模型影响.最后采用已有大量试验数据验证本文尺寸效应模型.本文得出主要结论如下.

(1) 通过对已有试验和理论研究的系统深入分析可得: 随着试件尺寸的增大,LDZ 尺寸逐渐非线性增大后趋于恒定.然后提出能准确描述LDZ 非线性尺寸效应的模型.在此基础上,建立考虑局部损伤区变化的能量平衡尺寸效应模型.

(2) 对考虑局部损伤区变化的能量平衡尺寸效应模型参数分析表明: LDZ 尺寸与试件尺寸相对变化率之间的竞争是本文尺寸效应模型能体现5 种类型的尺寸效应的原因;当LDZ 尺寸相对变化率大于试件尺寸相对变化率时,呈现上升尺寸效应;反之,呈现下降尺寸效应;当LDZ 尺寸相对变化率等于试件尺寸相对变化率时,呈现无尺寸效应现象.

(3) 应用考虑局部损伤区变化的能量平衡尺寸效应模型和IUSEL 预测类型3 和4 尺寸效应试验数据,结果表明: 考虑局部损伤区变化的能量平衡尺寸效应模型能很好预测各种材料类型3 和4 尺寸效应试验数据变化规律,而IUSEL 不能描述类型4 尺寸效应数据变化规律.考虑局部损伤区变化的能量平衡尺寸效应模型和IUSEL 预测所有尺寸效应数据的总平均确定系数接近.