湿热环境下多孔功能梯度圆管的非线性弯曲行为1)

陈 央 刘晓军 彭旭龙 陈得良

(长沙理工大学土木工程学院,长沙 410114)

引言

为开发性能更优的轻量化结构,人们开始结合仿生复合材料进行结构创新[1],通过模仿天然骨骼和木材引入内部孔隙,从而改变材料的密度.功能梯度材料[2](functionally graded materials,FGM)与孔隙结合就是重要的发展趋势之一.多孔FGM 结构具有分离过滤、阻燃防爆等功能,在航空航天、土木工程、海洋工业等领域得到了广泛的应用[3-6].

功能梯度材料在温度和湿度不断变化的复杂环境中服役时,其材料特性会发生变化.近年来,许多学者研究了复杂环境下FGM 结构的力学行为.李世荣等[7]研究了热环境中粘贴压电层功能梯度材料矩形梁的自由振动问题.许新等[8]研究了FGM 矩形截面微梁的热弹性阻尼.范纪华等[9]研究了热环境下FGM 变截面矩形梁的动力学问题.Nikrad 等[10]研究了多孔FGM 矩形截面曲梁的面内热弹性响应.Akbas[11]分析了湿热环境下FGM 悬臂矩形梁的非线性弯曲行为.Tang 等[12]研究了湿热环境下FGM 矩形梁的非线性振动问题.Ansari 等[13]对湿热环境下多孔FGM 矩形梁进行振动分析.Wang 等[14]研究了湿热环境下多孔FGM 矩形梁的热弹性动力响应问题.李清禄等[15]研究了湿热环境下多孔FGM矩形梁的后屈曲和屈曲问题.Wang 等[16]研究了湿热环境下多孔FGM 矩形微梁的屈曲行为.Wang 等[17]研究了湿热环境下多孔FGM 矩形微梁的弯曲和自由振动特性.Jouneghani 等[18]研究了湿热环境下多孔FGM 矩形微梁的弯曲行为.戴婷等[19]研究了湿热环境下旋转变厚度多孔FGM 圆板的湿热力学响应问题.Pham 等[20]研究了湿热环境下多孔FGM 矩形截面曲梁的自由振动问题.

上述文献中研究的是矩形截面梁和圆板.圆管作为一种常见且重要的基本结构,广泛应用于管道、支柱、横梁、机械设备和机器等部件中.已有许多学者采取不同的梁理论对圆管进行研究.基于Euler 梁理论,部分学者研究了圆管的静动力学问题[21-23].为考虑短粗梁中的横向剪切变形,Timoshenko梁理论被广泛应用于圆管的非线性静动力学问题[24-26].Euler 梁理论只适用于细长梁,Timoshenko 梁理论可以分析含横向剪切变形的短粗梁,然而Timoshenko梁理论针对不同的梁截面需要选取合适的剪切修正因子.且上述两种梁理论均不能满足圆管内外表面剪应力为0 的边界条件.为此,Zhang 等[27]提出了一种适用于圆管的高阶剪切变形梁理论,该梁理论可以满足内外表面剪应力消失的应力边界条件,能很好地反映圆截面的几何特征.基于该梁理论,Liu 等[28]研究了在不同分布载荷作用下层合管的非线性弯曲.She 等[29-30]研究了多孔纳米管的非线性弯曲和振动[29]、屈曲和后屈曲[30]特性.

综上所述,采用修正的高阶剪切变形梁理论对湿热环境下多孔FGM 圆管的非线性弯曲行为的研究较少.本文采用修正的高阶梁模型,对多孔FGM圆管在湿热环境中的非线性弯曲行为进行研究.基于修正的高阶剪切变形梁理论,考虑温度对材料属性的影响,通过最小势能原理,得到湿热环境下多孔FGM 圆管的非线性弯曲控制方程,采用二次摄动法对控制方程进行求解,并与已有文献的结果进行对比以验证本文方法的正确性,通过数值算例讨论不同参数对多孔FGM 圆管的非线性弯曲行为的影响.

1 基本方程

考虑处于湿热环境中,并受横向均布载荷q作用的多孔FGM 圆管,其长度为L,内半径为Ri,外半径为Ro,为便于研究,建立直角坐标系O(x,y,z)和柱坐标系O(x,r,θ),如图1 所示.显然,y=rcosθ,z=rsinθ,r2=y2+z2.

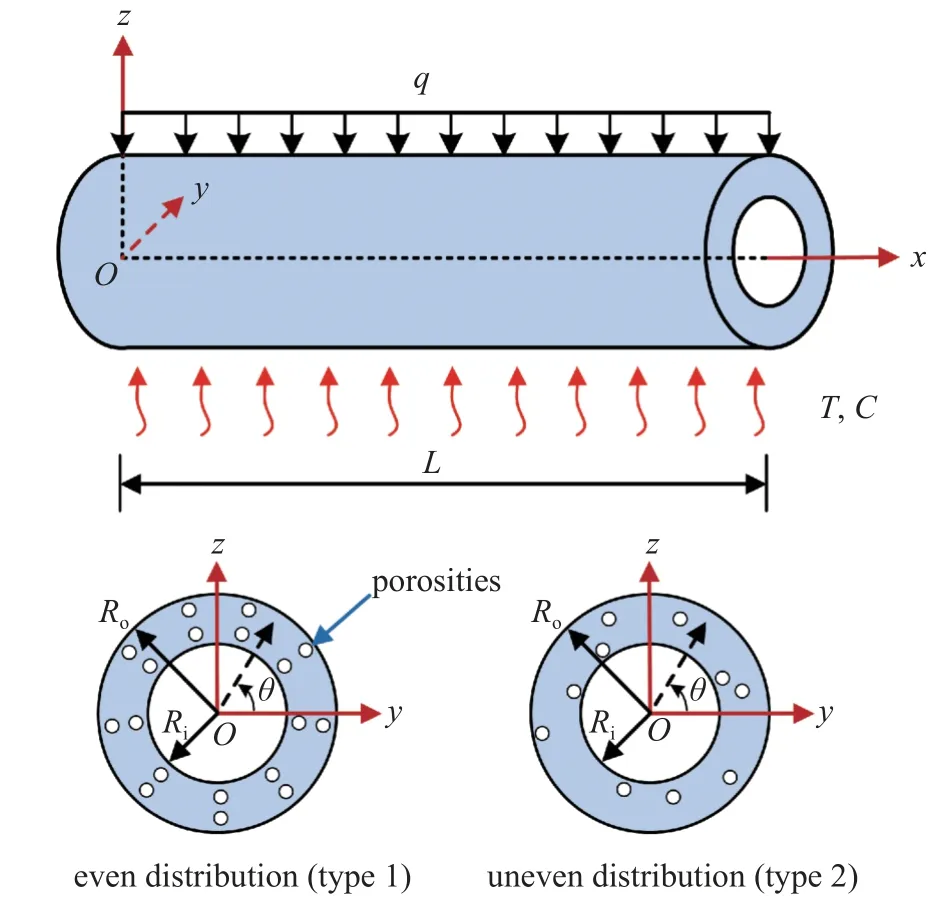
图1 多孔功能梯度材料圆管的示意图Fig.1 Schematic diagram of the FGM porous tube

考虑均匀和非均匀的两种孔隙分布模型[30],如图1 所示.

均匀孔隙分布模型(type 1)如下

非均匀孔隙分布模型(type 2)如下

式中,ζ(ζ ≪1)表示孔隙率,N是一个非负的梯度指数,P表示材料属性,包括杨氏模量E、质量密度 ρ、热膨胀系数 α和湿膨胀系数 β等.下标f,m和c分别表示多孔FGM、金属和陶瓷.

基于Zhang 等[27]的高阶剪切变形梁模型,位移场如下

其中,u1和u3是任意一点沿着x和z方向的位移,u0和w分别为多孔FGM 圆管中平面x方向和z方向的位移,φ为横截面的转角,下标","表示对后面变量求偏导.当f=0时,该梁模型退化为Timoshenko 梁模型; 当f=−z时,该梁模型退化为Euler 梁模型.

由von Kármán 非线性应变−位移关系可得轴向应变 εx、剪切应变 γxy和 γxz为

考虑湿热环境下多孔FGM 圆管的物理方程为

其中,σx表示轴向应力,τxy和 τxz表示剪应力,G表示剪切模量,ΔT和ΔC为温度和湿度的变化量.

多孔FGM 圆管的非线性弯曲控制方程可由最小势能原理导出,其总势能为

其中,U为应变能,Ue为外力势能,A表示多孔FGM 圆管的横截面面积.

根据最小势能原理 δΠ=0,可得由内力表示的平衡方程

其中,内力为

由式(9)可得

其中,NT和NC是由热载荷和湿载荷引起的轴力,其表达式为

且Ai(i=0,1,2,3,4)的表达式为

考虑具有两端简支面内不可动支撑的多孔FGM圆管,其边界条件为

由方程组(8) 的第一式和边界条件(12) 中的u0(0)=u0(L)=0,可得

将式(5)和式(6)代入式(8),可得由位移分量w,φ表示的控制方程

为方便研究,引入如下无量纲参数

式中E0为梯度指数N=0时圆管的弹性模量.

将式(15)代入式(14),得到无量纲控制方程为

2 求解方法

式(16)为非线性常微分方程组,采用二次摄动法[31]进行求解.位移W、位移 Φ和载荷 λq展开为

其中,ε为小摄动参数.

将式(17)代入式(16),并按照 ε的同次幂进行离散展开,逐阶求解,可得渐进解形式为

其中,Wm为梁的中点挠度.

将式(20)代入式(19),可得

3 数值分析

表1 为陶瓷(Si3N4)和金属(SUS304)的材料参数.材料的温度相关性可由以下非线性方程描述

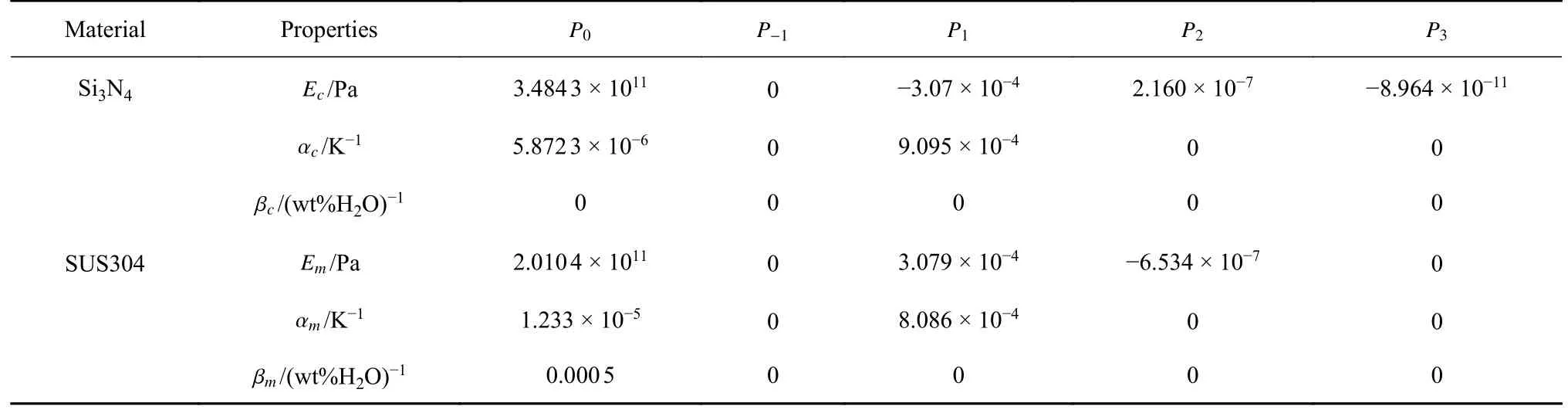
表1 陶瓷(Si3N4)和金属(SUS304)的材料属性Table 1 Material properties for Si3N4 and SUS304

其中,P−1,P0,P1,P2,P3是与温度有关的材料系数.

考虑湿−热均匀分布

其中,T和C分别表示温度和湿度,T0和C0表示无应力状态时的参考温度和湿度,取T0=300 K,C0=0%.

为验证本文模型和方法的正确性,不考虑湿度和孔隙,取材料参数和材料尺寸与文献[32]一致,并将本文与其结果进行了对比,如图2 所示.其中横坐wm/Ro是无量纲的挠度.由图2 可知,两文结果吻合,表明了本文所采用的理论模型和求解方法的有效性.标

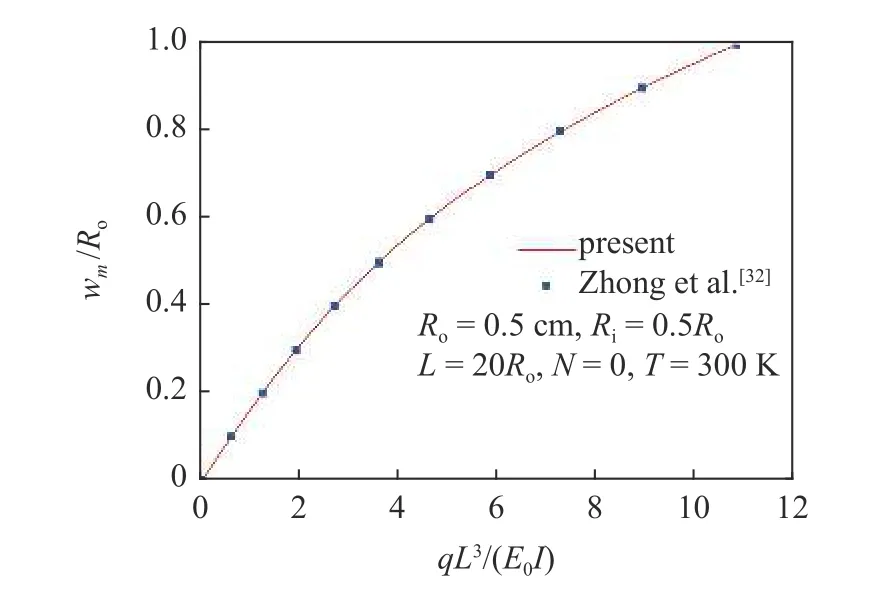
图2 圆管的非线性弯曲响应曲线的对比Fig.2 Comparisons of nonlinear bending responses for tube

图3 给出了不同梁模型下多孔FGM 圆管的非线性弯曲响应曲线.当L=5Ro时,本文的高阶剪切梁模型和Euler 梁模型所得的结果有一定差异; 当L=20Ro时,不同梁模型的结果基本相同.这表明当圆管的长细比较小时,圆管的横向剪切变形影响较为明显,需要考虑剪切变形对弯曲的影响.

图3 不同梁模型多孔FGM 圆管的非线性弯曲响应Fig.3 Nonlinear bending responses of FGM porous tubes under different beam models

图4 和图5 分别为孔隙率 ζ对多孔FGM 圆管非线性和线性弯曲响应的影响.由两图可知,随着孔隙率 ζ的增加,圆管的弯曲变形增大,这是因为孔隙的增多导致圆管的弯曲刚度降低,从而使圆管更容易发生变形; 当孔隙率越大,均匀孔隙圆管的弯曲响应明显大于非均匀孔隙圆管的弯曲响应,这表明在高孔隙率的情况下,非均匀孔隙分布可以有效提高圆管的抗弯曲变形能力.将图4 和图5 对比可知,在弯曲变形较大时,考虑非线性弯曲是十分必要的.

图4 孔隙率 ζ对多孔FGM 圆管非线性弯曲响应的影响Fig.4 Effect of porosity on nonlinear bending responses of FGM porous tubes

图6 为梯度指数对多孔FGM 圆管非线性弯曲响应的影响.由图可知,随着梯度指数的增加,圆管的弯曲变形越明显,原因是随着梯度指数的增加,圆管的弹性模量会降低,使得梁更容易发生变形.

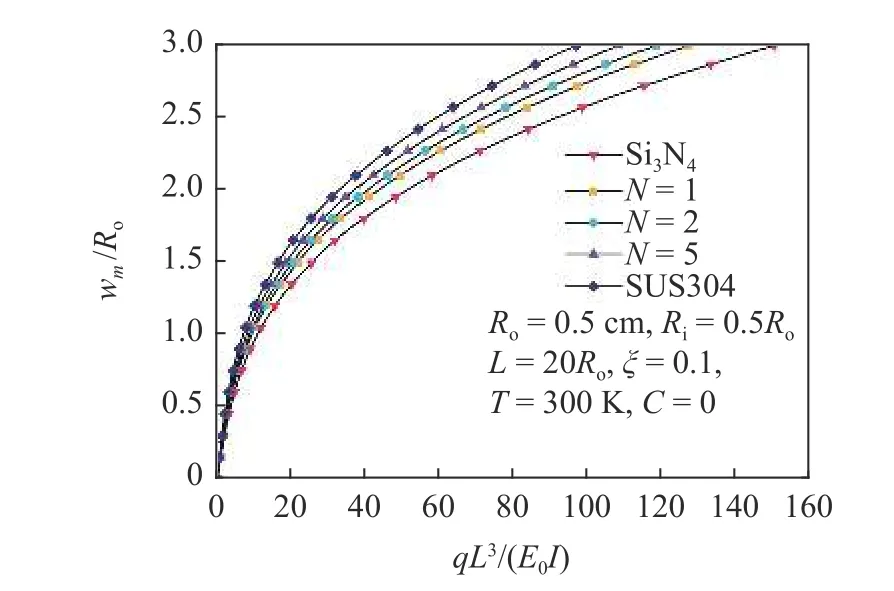
图6 梯度指数对多孔FGM 圆管非线性弯曲响应的影响Fig.6 Effect of volume fraction index on nonlinear bending responses of FGM porous tubes

图7 揭示了圆管内半径Ri对多孔FGM 圆管非线性弯曲响应的影响.由图可知,圆管内半径Ri的增大导致其弯曲变形程度越明显,原因是圆管内半径Ri的增大会使圆管薄壁化,这种薄壁化使得圆管的弯曲刚度降低,让圆管更容易发生变形.

图7 内半径 Ri 对多孔FGM 圆管非线性弯曲响应的影响Fig.7 Effect of inner radius Ri on nonlinear bending responses of FGM porous tubes

图8 给出了湿度对多孔FGM 圆管非线性弯曲响应的影响.由图可知,湿度越大,圆管弯曲变形越大,但湿度对于圆管弯曲变形影响很小,这是因为材料的湿膨胀系数很低,对湿度变化不敏感.

图8 湿度对多孔FGM 圆管非线性弯曲响应的影响Fig.8 Effect of humidities on nonlinear bending responses of FGM porous tubes

图9 研究了温度对多孔FGM 圆管非线性弯曲响应的影响.温度的升高会使得圆管弯曲变形增加.

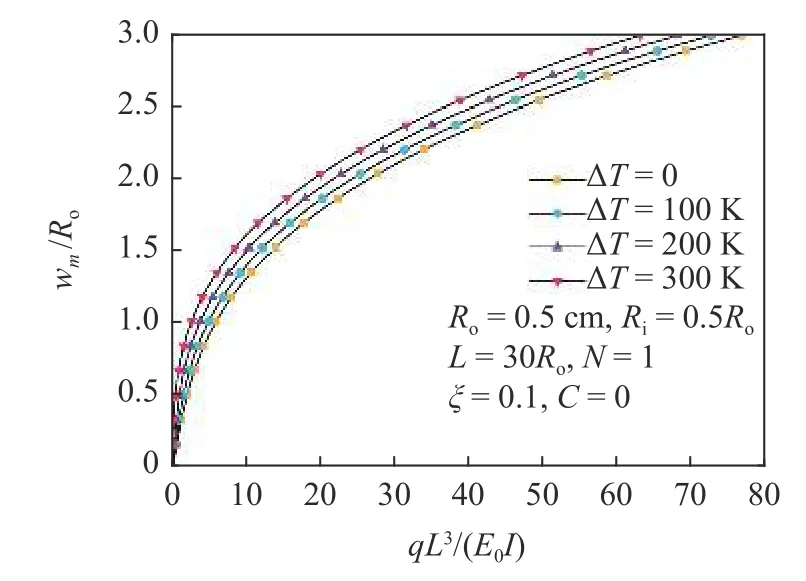
图9 温度对多孔FGM 圆管非线性弯曲响应的影响Fig.9 Effect of temperature on nonlinear bending responses of FGM porous tubes

4 结论

本文基于一种修正的高阶剪切变形梁理论,讨论了孔隙分布模型、孔隙率、梯度指数、内半径、湿度和温度对湿热环境下多孔FGM 圆管的非线性弯曲行为的影响,主要结论如下:

(1) 二次摄动法可以准确高效求解非线性弯曲问题,并且能得到问题的半解析解,便于对此类问题进行定量和定性的讨论;

(2) 当孔隙率较大时,非均匀孔隙分布可以有效提升圆管的抗弯曲变形能力,因此在实际轻量化设计过程时,孔隙分布优先采用非均匀分布模型;

(3) 短粗梁需要考虑横向剪切变形,采用的修正的高阶梁模型可以精确研究不同长细比的圆截面梁问题;

(4) 随着湿−热加剧,多孔FGM 圆管的弯曲变形越大,考虑温度和湿度的影响对服役过程中的多孔FGM 圆管十分必要.