基于改进A星算法的无人机自主避障路径规划

高九州,徐威峰

吉林建筑大学,吉林 长春 130118

0 引言

近年来,无人机技术发展越来越成熟,无人机具有使用方便、能够执行复杂且危险的任务、生存能力较强的特点。工业、物流和救援等领域,因越来越多的无人机加入,其工作效率得到显著提高。无人机的使用涉及很多技术,其中关键的一个技术问题就是路径规划。在任务空间的大环境不变的情况下,当确定无人机起始点和目标点之后,无人机避障路径规划问题的研究主要集中于路径最短、耗能最少、路径规划时间最小等。通过对任务环境数据采集、分析、计算与比较,使用相关的避障算法规划出安全、最优和无碰撞的路径[1]。

路径规划问题是国内外学者研究的热点,无人机自主避障路径规划分为二维和三维2种情况[2],本文主要研究二维平面情况下的路径规划问题。避障路径的规划算法分为局部动态路径规划算法和全局静态路径规划算法[3]。局部动态路径规划算法是指无人机在飞行过程中不知道周边环境信息[4],在飞行中可能遇到变化的环境信息,只能依靠无人机上自带的一些传感器来感知飞行环境周边信息,根据周边环境的实时情况建立动态模型,再通过CPU进行分析、计算规划出一条避开障碍物的最优路径,是一种边飞边设计的航线。全局静态路径规划算法是指无人机飞行前已知周边环境,通过对该飞行范围环境的建模,然后以一些约束和标准,规划出一条从起点到目标点绕过障碍物的最优路径[5]。

在全局静态路径规划算法中A星算法是现在使用最多的路径规划算法之一。A星算法是对Dijkstra算法和贪心算法的借鉴与改进,在1968年由美国研究者提出,是一种基于启发式搜索策略兼顾搜索效率和最优航迹的算法,该算法改变了Dijkstra算法中无序搜索的情况,因此该算法成为栅格法建模路径规划的主要算法之一[6]。但A星算法存在搜索节点过多、搜索效率低、规划出来的路径转折点和冗余点较多的问题。

本文提出一种改进型A星算法。首先,该改进型A星算法充分考虑无人机本身的物理信息问题,对传统A星算法的子节点扩展规则进行改进,保证无人机在飞行过程中与障碍物始终保持一种安全距离,防止撞机。其次,对传统A星算法的评价函数进行改进,提出了一种定义障碍率加权的启发函数,从而减少搜索节点和搜索区域,节约搜索时间,提高搜索效率。最后,结合Floyd算法原理,删除了一些多余的节点,航迹中的转折变少,使转折角变得平缓,使得航迹得到改善,保证无人机行驶安全、平稳、省时。

1 传统A星算法

1.1 建模处理

地图建模的方法主要包括栅格法、拓扑法、可视图法等[7-9],其中,将环境二维或三维地图根据栅格法进行分割,单位长度的栅格由实际的环境情况决定,比如无人机自身的一些物理信息。二维或三维静态环境中的障碍物信息用栅格法能被有效展示,因此本文使用MATLAB 2020b中的栅格法构建二维环境地图。

1.2 A星算法

A星算法汲取了Dijkstra算法与贪心算法的优点[9],核心是计算其扩展节点的代价函数,在扩展过程中,不断用代价值最小的节点作为子节点[10],并且以该子节点作为当前的父节点进行扩展与搜寻下个过程的子节点,将代价函数最小的子节点依次寻找出来,形成优化航迹。

F(n)评价函数的公式为:

F(n)=G(n)+H(n)

(1)

式中:G(n)为实际路径代价值从起点到当前点;H(n)为估计路径代价值从当前点到目标点。

欧几里得距离公式、曼哈顿距离公式和切比雪夫距离公式为计算G(n)、H(n)的3种计算方法。该文章采用欧几里得距离公式,其表达式为:

(2)

(3)

式中:(xi,yi)为当前节点;(xs,ys)为起点;(xt,yt)为目标点。

A星算法实质是扩展搜索过程中不断更新开和闭列表中的节点及其相关信息,通过比较计算每个扩展节点的评价函数值,选择代价函数值最小的一个节点作为下个步骤搜索的父节点,依次查找直至找到目标点,形成搜索路径。路径的优劣则主要依赖于评价函数的设计,因为如果搜索代价函数值每一步都是最小的,那么就能确保搜寻出来的路径也是最优的。但是,A星算法在运行中也存在一些未考虑的问题。

1)在栅格地图的二维空间中搜索方法为扩展8节点的,在路径搜索过程中算法搜索节点数量太多,因为每个节点的评价函数值都需要计算,这样每次计算将导致计算量过大,需要较长的计算时间,使其搜索效率低下。

2)该算法在进行航迹规划时,会产生多余点、转折点过多的情况,导致飞行路径有较多的转折,不能保证无人机的平稳飞行。

3)进行航迹规划时,该算法仅仅将障碍物节点信息考虑在内,并没有将无人机自身物理信息考虑在内,未考虑可能发生撞机时,无人机路径不能以栅格对角线的形式斜穿障碍物顶点的情况。

2 改进型A星算法

2.1 路径安全设计

本文对传统A星算法进行了路径安全改进设计,以二维空间环境为例,为防止撞机设置安全距离为1个栅格单位,如果存在障碍物节点信息在当前节点的左/右、上/下方向上,则不使用以对角线形式生成路径上的节点作为当前节点的扩展子节点,所以路径距离障碍物小于1个栅格单位安全距离的对角线不能生成航迹。

如图1所示,假设航点为A—B—C—D—E—F—G—H,B点上侧和E点左侧存在障碍节点,传统A星算法的最优扩展节点为A—B—D—E—G—H,但是,该路径距障碍点(3,7)和(3,3)的距离小于1个栅格单位,故B扩展子节点时不允许其扩展子节点C,E不允许其扩展子节点G,最佳子节点依次应为A—B—C—D—E—F—G—H。

图1 优化扩展子节点方式

如图2所示,节点A的1、3、5、7四个方向中任意节点为障碍点时,依次不允许生成0、2节点;2、4节点;4、6节点;6、5节点。通过此方法设计,防止无人机撞机。

图2 优化扩展子节点示意

图3为路径安全设计后的航迹。该路径安全设计对路径长度有略微增加,但能保证其形成航迹的安全性,防止撞机。

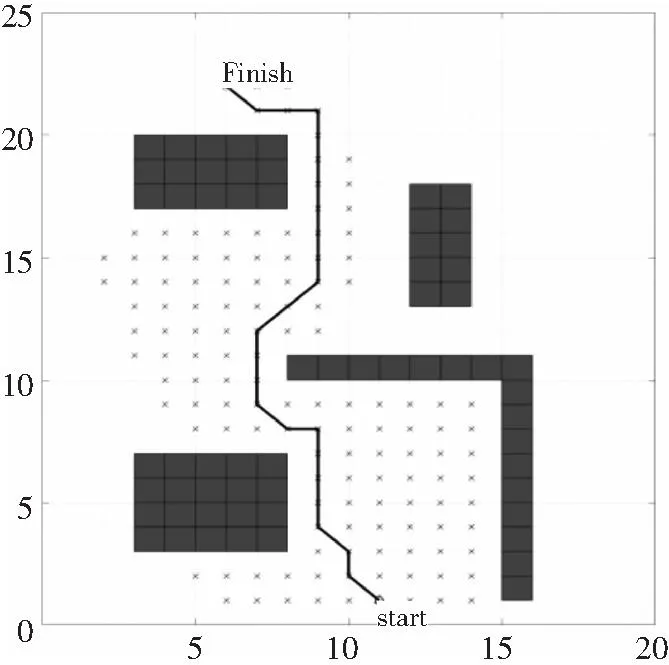
图3 优化扩展子节点生成的航迹

2.2 评价函数优化

传统A星算法以子节点的评价函数值为核心进行启发式搜索时,会在OPEN列表中不断计算搜寻总代价值最小的节点,这将造成传统算法不断进行往返搜索,大大增加了算法的计算时间,使其效率低下。

定义障碍率Q为在起点与目标点组成的局部环境中,障碍物栅格顶点坐标的个数与该范围内局部栅格地图坐标点个数之比。起点与目标点组成的局部栅格地图内的障碍物顶点个数为M,起点坐标(xs,ys)、目标点坐标(xt,yt),表达式如下所示。

对障碍率Q求对数,当栅格地图中该环境中的障碍率比较小时,可以直接向目标点所在方向进行搜索,让该算法的评价函数H(n)适当增大,提高该空间地图环境中目标点的方向性;当该栅格地图环境中障碍率比较大时,不能再进行增大评价函数H(n)的做法,如果增大太多让其只向目标点方向搜寻,会让算法陷入局部最优,同时使其距离代价变大,导致最优路径变的难以搜索。因此,当栅格地图环境中障碍物比较多,障碍率比较大时,应适当调整启发函数的值,让其适当减小,从而增大搜寻的范围,通过适当降低该算法的搜寻速度,提高搜寻的精度,以获得最优的航线。

F(n)=G(n)+βH(n)

β=1-lnP

式中:β为权重值;P代表障碍点Q在这个建模环境内所占比重。

与传统A星算法相比,改进后的算法其路径长度、搜寻节点数比较如表1所示。改进评价函数A星算法的对比仿真如图4～7所示。

表1 不同障碍率节点数与路径长度对比

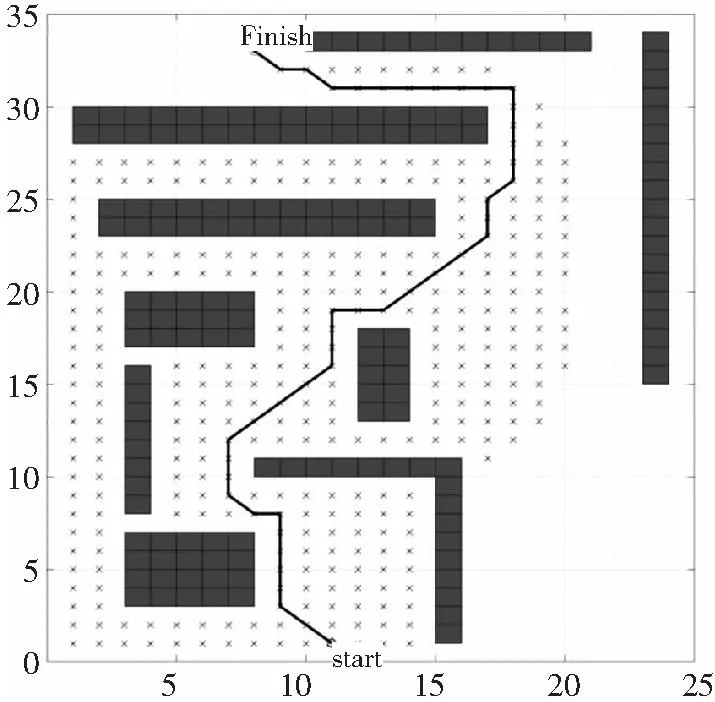
图4 障碍物多时启发函数未加权前A星算法路径

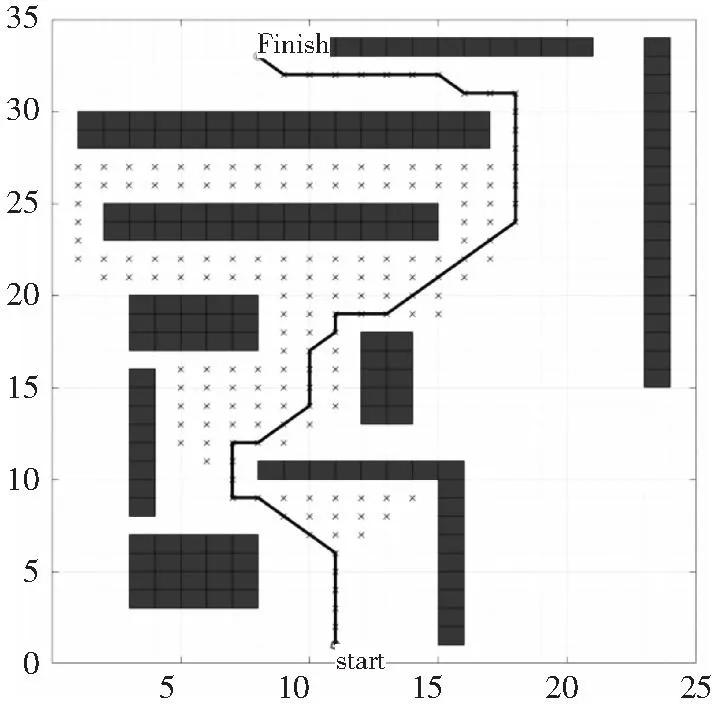
图5 障碍物多时改进启发函数加权为β1后A星算法路径

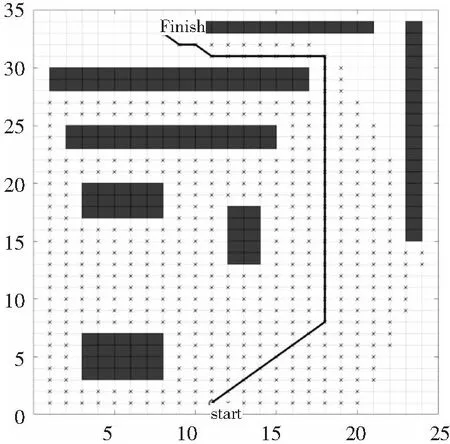
图6 障碍物少时启发函数未加权前A星算法路径

图7 障碍物少时改进启发函数加权为β2后A星算法路径

由表1可知,对该评价函数进行加权后,当障碍物比较少时往返搜索的节点少了近65%,闭环节点少了52%,显著减少了该算法往返一些节点无用搜寻的次数,显著提高算法的搜寻效率。当障碍物比较多时往返搜索的节点少了近40%,闭环节点少了28%,在保证其搜索精度的前提下,即减少了往返无用搜索的次数,也提高了算法的计算效率。

2.3 路径简化处理

当使用传统A星算法时生成的路径为A—B—D—F—G,由于只能沿着栅格点依次形成避障路径,因此会存在大量的冗余点和转折点。本文结合Floyd算法将传统A星算法中一些不必要的多余点和转折点进行简化删除,缩短路径的长度,对其生成的航迹进行优化处理,使航迹的转折角变得平滑,更有利于保证无人机飞行的连续性和安全性。

Floyd算法的基本原理如图8所示,传统A星算法规划出的路径为A—B—D—F—G,即每一步只能沿着栅格的正/负、上/下或对角线方向规划,但由图可知,节点B显然是多余的,即A—B—D的航迹不太合理,该航迹有转折且长。可将其简化为航迹A—C—D—G或航迹A—E—D—G,比较航迹A—C—D—G或A—E—D—G。在Floyd算法下,航迹A—D—G航迹虽然最短,但与障碍点距离小于安全距离,不合理,因此舍弃。航迹A—E—D—G则更加简短,更合理,符合航迹安全规则。故舍弃航迹A—C—D—G,选择较合理的航迹A—E—D—G。

图8 Floyd简化航迹规划原理

通过Floyd算法优化,删除了一些多余的节点,航迹中的转折变少,使转折角变得缓,使得航迹得到改善,保证无人机飞行过程比较安全、平稳、省时。

A星算法优化后的流程如图9所示。

图9 改进A星算法流程

3 改进A星算法的仿真和分析

在传统A星算法航迹规划的基础上,对其进行简化路径长度、路径安全设计、评价函数加权优化,然后在MATLAB 2020b中进行仿真测试与分析。

当起点坐标为(11,1)、终点坐标为(35,34)时,该栅格地图环境中设置7组障碍物。图10是未改进评价函数的航迹图,实线是在路径安全设计下的A星算法航迹,路径安全设计和Floyd简化航迹的设计下的航迹由虚线表示。对评价函数进行优化的航迹图如图11所示,在路径安全设计和优化评价函数条件下的A星算法航迹由实线表示,在路径安全设计、改进评价函数和结合Floyd简化航迹的设计下A星算法航迹由虚线表示。比较图10和图11可知,没有进行评价函数优化的航迹与进行评价函数优化的条件下航迹步数比较都为63,航迹步数一致。但是,在没有进行评价函数优化的搜索节点数量达到550个,进行评价函数优化后的搜索节点数量只有239个,其搜寻数量显著减少,显著提高了搜索效率。

4 结束语

本文在传统A星算法的基础上,通过对无人机避障航迹规划的问题进行优化处理,得出一种改进型A星算法。通过仿真验证了此改进A星算法的无人机自主避障航迹规划的合理性和有效性。改进型A星算法具有以下特点。

1)将无人机本身的物理信息考虑在内,进行路径安全设计的方法,保证障碍物坐标点与生成的航迹距离不小于设定的安全界限。

2)优化评价函数,进行加权处理,降低了算法搜寻时间,搜索效率得到提高。

3)结合Floyd简化航迹算法,优化了改进A星算法生成的避障航迹,在确保航迹符合无人机飞行安全界限时,删除多余节点,使规划出来的航迹比较平缓,减少航迹中的转折角,保证无人机从起点到终点的飞行安全平稳、用时较少。