汽车AFS/ESP 协调控制建模仿真及分析

韩 杰，孔庆研，董强强，曹 建，王志军

（中汽研（天津）汽车工程研究院有限公司，天津 300450）

主动前轮转向系统（Active Front Steering，AFS）与电子稳定系统（Electronic Stability Program）是汽车应用较多的底盘稳定性控制系统，对改善汽车的行驶稳定性具有极大的作用。AFS控制器通过给汽车前轮施加一个独立于转向系统的转角，改变轮胎侧偏角，使车轮侧向力发生变化，进而形成横摆力矩，从而提高汽车的行驶稳定性。ESP控制器根据方向盘转角变化获取驾驶意图，通过控制左右侧车轮产生不同的制动力，最终获得附加横摆力矩，使汽车按预期轨迹平稳运行。随着汽车控制系统的增加，各系统间的协调控制可以最大程度地发挥各系统的性能，降低成本以及系统的复杂性。

目前，汽车行驶稳定性协调控制已经成为汽车稳定性研究的重点。Kunsoo Huh[1]应用模糊理论搭建了主动转向系统，并通过道路试验研究了汽车在路况较差情况下的转向问题。Li J W和Cui X L[2]应用滑模控制理论，建立了使用质心侧偏角和横摆角速度作为输入的直接横摆力矩控制器。Yim S J[3]等搭建了电动助力转向系统和主动前轮转向系统，并将两者进行协调控制，取得了较好汽车稳定性控制效果。杨亚飞[4]基于相平面理论，应用相平面图确定汽车稳定域，并根据AFS和DYC的特点，确定协调控制策略，改善了整车行驶稳定性。但在研究稳定性控制器时，实车模型较为简单，导致精确性不高，且使用汽车行驶状态对控制器进行协调控制的情况较少。

本文构建基于主动前轮转向控制器和汽车电子稳定控制器，进而基于汽车的运动状态，将二者进行协调控制，设计整车稳定性控制器，并构建Carsim模型作为实车模型，通过Carsim/Simulink联合仿真，对比分析3种控制器对汽车行驶稳定性的控制效果。

1 车辆模型

传统二自由度数学模型简化如图1所示[5-6]。图中α1与α2分别表示汽车前后轮侧偏角，汽车的侧向运动和横摆运动如下：

图1 传统二自由度数学模型

式中：Iz—绕z轴转动惯量；a—前轴距；b—后轴距；k1——前轴侧偏刚度；k2—后轴侧偏刚度；m—整车质量；vx—汽车纵向速度；vy—汽车侧向速度；β—质心侧偏角；δ—前轮转角；ωr—汽车横摆角速度。

汽车线性二自由度虽然简单，但它建立了一定前轮转角输入情况下，前后轮侧偏刚度和整车参数与整车运动状态之间的关系，在一定程度上可以表示汽车的运动特征。

参照式（1）所得汽车二自由度方程，将该方程转化为状态空间方程作为理想汽车参考模型，二自由度方程变形为[7]：

式中：A、B、C、D、E、E、F——汽车参数。其中：

2 AFS和ESP控制器设计

2.1 AFS控制器设计

为改善汽车的行驶稳定性，设计以横摆角速度作为控制变量的滑模变结构控制器。此时，横摆角速度误差定义为：

式中：ωr——实际横摆角速度；ωd——理想横摆角速度。

设计切换面函数为：

式中：λ0——滑模面系数，其值恒大于0。

将切换面函数求导：

由状态空间方程可得：

将式（6）和（7）联立可得滑模面函数的导数：

为保证滑模变结构控制性能，选择等速趋近法降低系统抖振：

式中：ε——系统中运动点移动速度，ε必须满足如下条件：

本文使用饱和函数代替符号函数，以进一步消除抖动，即

最终AFS滑模控制律为：

式中：Ω——滑模面厚度。

所得的控制律函数通过Simulink模块搭建出仿真程序，构建出基于滑模变结构控制的AFS控制器。

2.2 ESP控制器设计

2.2.1 模糊PID控制器设计

自适应模糊PID控制[8]是一种在PID控制的基础上，运用模糊数学的基本原理，将规则用模糊集表示，并将其输入到计算机中，计算机根据控制系统的情况，运用设计的模糊规则，实现自动调整PID参数的控制方法。模糊PID控制具有模糊控制和PID控制各自的优点，能够消除稳态误差，而且控制参数受数学模型的影响较小，因此，这一控制方法具有较高的控制精度。

自适应PID控制系统的输入是误差e和误差变化率ec，制定e和ec与PID参数之间的模糊关系，并在运行的系统中不断对输入值进行检测，根据模糊规则对PID参数进行实时调整。

本文应用自适应模糊PID算法来设计ESP上层控制器，将横摆角速度偏差e和质心侧偏角偏差ec作为输入参数，补偿横摆力矩ΔM为输出参数，模糊控制规则中，输出变量为PID修正参数ΔKP、ΔKi、ΔKd。

输入变量e和ec模糊论域分别为[-30，30]和[-1，1]，输出 量ΔKP、ΔKi、ΔKd的模糊论域分别为[0，15]、[0，4]和[0，0.4]。将输入变量e和ec的基本论域设定为[-1，1]，则e的量化因子为1/30，ec的量化因子为1。输入和输出变量语言为：负大（NB）、负中（NM）、负小（NS）、零（O）、正小（PS）、正中（PM）、正大（PB）,本文将采用三角形隶属函数设计输入与输出变量的隶属函数。

作为模糊控制器的核心，建立的模糊规则要做到减小系统误差超调量。因此，在理论分析的基础上，借鉴专家的研究经验，可得系统输入与输出变量的整定原则如下所示。

1）当e的绝对值较大时，可选取较大的ΔKP和较小的ΔKi来防止瞬时偏差过大和系统超调量增大。

2）当e和ec的绝对值大小适中时，可选取较小的ΔKP的值，使得系统有较快的响应速度和较小的超调量。

3）当e的绝对值比较小时，可选取较大的ΔKP和ΔKi，使系统具有较快的反应速度和较小的超调量，同时应该选取适中的ΔKd，使系统具有一定的稳定性。

根据上述规则，所建立的模糊规则如表1所示。

表1 ΔKP、ΔKi、ΔKd模糊规则表

则最终PID参数值数值如式（13）所示，KP0、Ki0和Kd0为PID参数的初始设定值。

2.2.2 力矩分配控制器设计

力矩分配控制器作用是将ESP上层控制器中计算的附加横摆力矩转化成各车轮的制动力。本文采用差动制动方式，通过单独控制左侧车轮制动力，来产生附加横摆力矩，则附加横摆力矩可表示为：

式中：Fx1，Fx2——汽车左前轮和左后轮制动力；df、dr——汽车前后轴之间的轮距。考虑到前轮转角较小，且认为前后轴轮距差距也较小，则上式可以写为：

轮胎制动力由前后轮所受垂直载荷比例来决定，为充分发挥路面附着条件，可以采用下式来动态分配轮胎制动力。

则车轮制动器提供左侧车轮的制动力矩为：

式中：R1、R2——前后轴轮胎的滚动半径。同理，可以求得汽车右侧车轮需要的前后车轮制动力和制动力矩[9]。

将所得的自适应模糊PID控制器和力矩分配控制器通过Simulink模块搭建出仿真程序，最终构建出基于自适应模糊PID控制的ESP系统。

3 协调控制方法分析及设计

3.1 Carsim实车模型建立

Carsim软件具有可靠性、实用性以及方便操作等优点，现已被全球汽车科研院所和生产厂商广泛使用，成为汽车动力学分析的一款重要软件。其模型在计算机中有着非常高的运行速度，可以对汽车平顺性、制动性和操纵稳定性等性能做出很好的预测，因此被广泛应用于汽车开发行业。本文选用Carsim中自带的一款车型C-Class Hatchback作为实车模型，并在软件中读取汽车主要参数带入到汽车理想模型中，用于搭建汽车稳定性控制器，其中实车参数见表2。

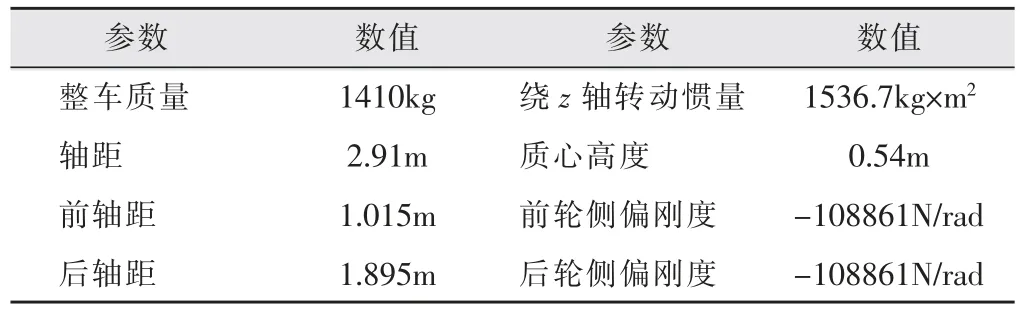
表2 实车参数表

3.2 协调控制策略

汽车稳定性的集成控制方法被国内外专家分为3类：集中控制、分散控制和协调控制。集中控制通过将多个子系统进行融合，建立大型的整体模型，并使用一个集中控制器进行集中控制。但集中控制的模型建立比较复杂，控制效果不能保证，因此并不常见。分散控制是对每一个子系统分别建立模型和控制器，并对各个子系统进行单独的控制。但在进行分散控制时，并没有考虑各子系统模型之间的耦合关系和相互影响，因此系统的控制效果有时并不理想。协调控制是对每一个子系统分别建立模型和控制器，再应用协调控制器来协调各子系统之间的影响，具有模型简单、控制效果精确等优点。因此，本文将使用协调控制来进行AFS和ESP系统的集成控制。协调控制的总体结构如图2所示，协调控制器通过获取汽车行驶状态以及实车模型与理想模型的误差，从而确定两控制器的占比，实现协调控制。

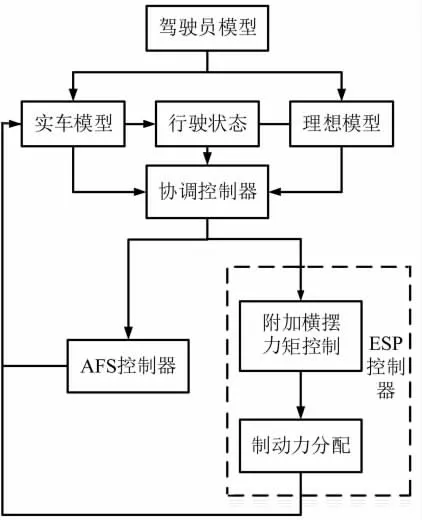
图2 协调控制结构图

协调控制算法主要根据汽车行驶状态对AFS控制器和ESP控制器控制权重分配。因此，对于汽车行驶状态的识别是否正确，将对协调控制的结果产生极大的影响。

将车辆的二自由度线性模型进行推导，可得其特性方程：

根据Hurwite稳定性判断依据，系统稳定的条件为：

经化简可得：

将v2ch定义为特征车速，系统稳定性判断依据为[10]：

由式（21）可知，汽车稳定性取决于汽车实际车速与特征车速的比值。由式（20）可得，特征车速为一常数，且可为负数。但是，汽车在实际行驶中，由于汽车的结构参数发生了变化，导致特征车速改变。因此，需要对特征车速公式进行推导。

假设汽车正在做稳态圆周运动，则其稳态横摆角速度为：

经推导可得：

式中，可将车速与转向半径关系近似为ωr=u/ρ，其中，ρ为转向半径。

在车辆转向半径固定、车速较慢、侧向加速度几乎为0时，前轮转角可定义为：

将式（24）带入到式（23）中，可得：

汽车稳态转向类型判断方法为：

综上所述，汽车行驶状态的判断过程为：首先利用车速、横摆角速度和前轮转角来判断汽车的特征车速，然后根据特征车速与实际车速的比值，判断汽车的稳态转向类型，最后使用方向盘转角观察车辆是否直线行驶。根据汽车的行驶状态，制定出汽车AFS和ESP协调控制策略。控制策略见表3。

表3 AFS和ESP协调控制策略表

表3中，ωr-lim为横摆角速度临界值，当直线行驶时汽车横摆角速度超过该值，则视为汽车受到外界干扰。AFS与ESP系统的协调控制权重是由转向时轮胎力对各变量的影响决定的，采用模糊控制法，选取输入变量为前轮单位垂直载荷的侧向力和前轮侧偏角，输出变量为ESP控制的比例系数。

其中，根据线性二自由度模型，前轮质心侧偏角可以表示为[11-12]：

此外，通过对线性二自由度模型进行简化，可得前轮单位垂直载荷的侧向力：

式中：ΔM——由ESP系统提供的附加横摆力矩。

经由多工况仿真与试验，可将输入变量FNyf和βf的模糊论域设为[0，10]，输出变量W的模糊论域设为[0，1]。

模糊控制输出作为AFS和ESP系统的控制权重，模糊控制器根据不同的工况来调整两种控制器的占比，使其在控制性能上获得较好的控制结果。根据大量试验可得控制规则，如表4所示。

表4 协调控制模糊规则表

将分配系数W带入到两控制器中，所得协调控制器的输出为：

4 仿真验证

4.1 双移线工况仿真

双移线工况仿真条件参照国际标准，车速为80km/h，道路附着系数为0.3。仿真结果如图3所示。

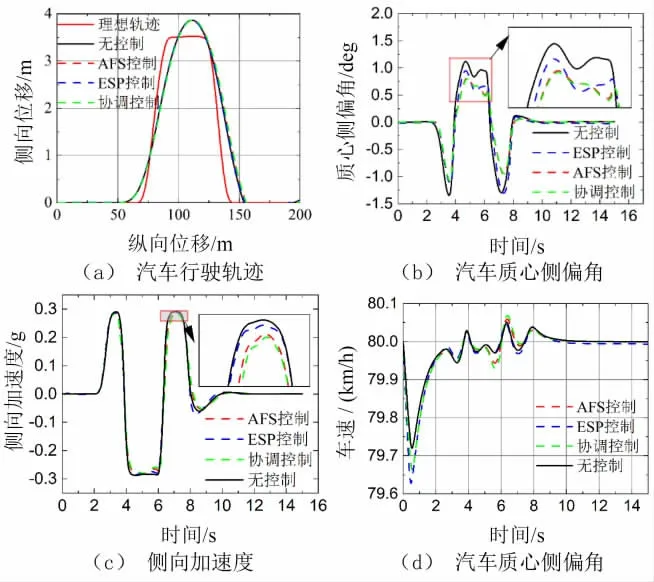
图3 协调控制双移线仿真结果

由图3a可以看出，有无控制系统的汽车行驶轨迹和理想轨迹都相对重合，表明汽车均可顺利通过双移线轨道，具备一定的路径跟踪能力。如图3b～3d所示，使用协调控制汽车的质心侧偏角和侧向加速度明显小于ESP控制汽车，略小于AFS控制汽车，且车速变化较小，汽车行驶稳定性较好，表明在保证汽车通过性的前提下，通过将侧向力和纵向力协同控制，能够更好地改善汽车的行驶稳定性。

4.2 方向盘角阶跃工况仿真

方向盘角阶跃工况仿真条件参照国际标准，车速为100km/h，道路附着系数为0.85，在第2s时，方向盘转角输入为1rad。仿真结果与仿真曲线如图4和表5所示。

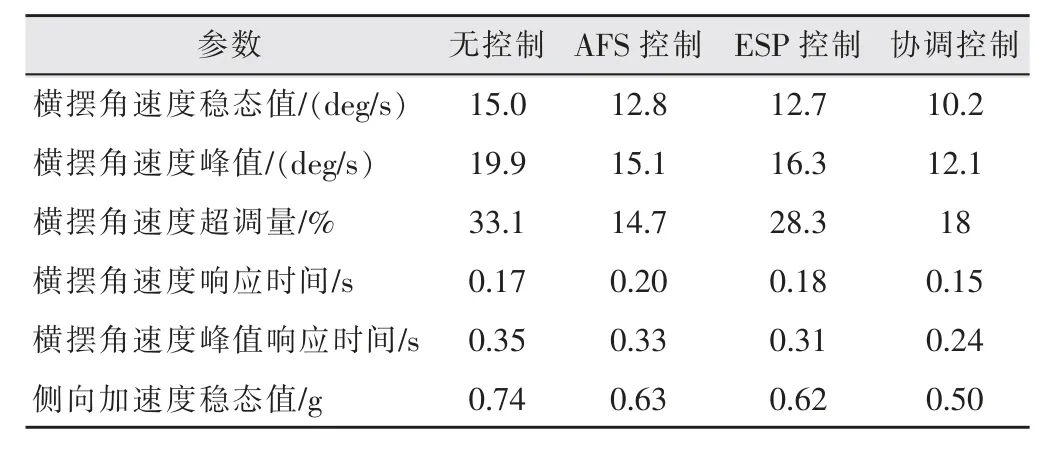
表5 协调控制器方向盘角阶跃工况仿真结果

图4 协调控制阶跃仿真结果

由表6可以看出，协调控制汽车比单独控制汽车具有更小的侧向加速度和更短的稳定时间，较小横摆角速度超调量，车速未产生较明显的变化。说明协调控制汽车在保证汽车性能的前提下，具有更好的稳定性。同时验证了在侧向力和纵向力控制器的协调作用下，汽车具有更好的操纵稳定性。

5 结论

1）本文应用滑模变结构控制理论，建立了以横摆角速度为控制目标的AFS控制器，应用模糊PID控制理论建立了以质心侧偏角和横摆角速度为控制目标的ESP控制器，最终应用Simulink搭建仿真程序。

2）根据路面的行驶状态，设计AFS和ESP协调控制策略，建立协调控制器。应用Carsim建立实车模型，通过与Simulink联合仿真，最终建立了联合仿真程序。

3）将建立的3种控制器进行双移线工况和方向盘角阶跃工况仿真，对比仿真结果。仿真结果表明，应用协调控制器的汽车在进行仿真时，具有更好的行驶稳定性。