一种基于几何关系的无人机航迹规划方法
张 敬,李 彤,杨 钧,朱得糠,张士峰
(1.国防科技创新研究院 无人系统技术研究中心, 北京 100071; 2.国防科技大学 空天科学学院, 长沙 410073)
0 引言
近年来,随着商用无人机产业的崛起,无人机技术得到了快速发展与迭代,无人机制造成本不断下降,应用范围也更加广泛,涉及了侦查探测、植保安防和巡检测绘等大量军用及民用领域,并逐渐向智能化应用方向拓展[1]。
无人机飞控计算机通常基于ARM或PowerPC架构进行开发,并且伴随芯片技术的不断提升,飞控计算机算力已非常强大,飞控相关技术由于开源化也相对成熟。然而面临复杂任务,无人机机载计算机一般采用任务计算机和飞控计算机组合的形式,任务计算机负责上层任务规划、深度感知、策略制定和集群通信等计算复杂度高而实时性要求低的工作,飞控计算机仅面向传统导航制导控制以及底层硬件驱动等计算复杂度低但实时性要求高的功能。这种形式使得飞控计算机算力在一定程度上有所浪费,并且考虑到无人机未来小型化和低成本化的发展趋势,轻小型无人机从载重和体积上都难以搭载任务计算机,因此,针对常规任务算法的优化对于拓展轻小型无人机任务功能十分必要。
无人机在飞行任务执行过程中,通常会面临较多地形地势障碍或拒止威胁区域,因而无人机航迹规划成为任务安全和飞行可靠的重要保障。航迹规划作为无人机规避障碍和威胁的必要技术,得到广泛的研究与关注,并且形成了较多成熟的算法,主要包括基于全局动态搜索的方法如Dijkstra算法[2-3]、A*算法[4-6]、Voronoi图法[7-9]和快速扩展随机树[10-12]等,基于启发式学习的方法如遗传算法[13-14]和粒子群算法[15-16]等,以及基于数理关系的方法如人工势场法等[17-20]。其中,A*算法和人工势场法在工程中应用较为广泛。A*算法优化性能较好,广泛应用于全局路径规划,但是类似于其他全局动态搜索算法和启发式学习算法,规划空间均需要通过地图栅格化、离散化或者重建路径的方式进行全局化建模,因此存在内存占用大、搜索时间长等问题,仅适于静态规划。人工势场法是一种动态连续算法,它的基本思想是把环境根据目标和障碍建模为虚拟力场,目标点产生引力,障碍点产生斥力,从而引导对象远离障碍点向目标点运动,但该算法也存在一些缺点,如当目标点附近有障碍点时,斥力远远大于引力,规划对象将很难到达目标点,又或当对象在某一点的引力和斥力刚好大小相等时,将陷入局部最优点。
由此,为充分利用飞控计算机算力,同时提高算法效率和保证算法性能,本研究中提出了一种基于几何关系的航迹规划与区域避障算法,能够避免规划空间全局离散化表示,大幅降低算法计算时间,有效规避障碍区域,并且支持动态实时上传障碍区域,在采用航迹点通用表示方法基础上考虑了无人机转弯半径,无需对航迹表示进行平滑处理。
1 问题描述与空间表示
航迹规划问题是一个综合考虑多目标多约束的非线性规划问题[21],其求解复杂度很大程度依赖于问题建模。为提高算法计算效率,本研究中航迹规划问题主要考虑二维情形下,无人机针对给定障碍和威胁区域,从初始点至目标点的飞行航迹规划和区域避障。障碍区域采用多边形点集形式,规划航迹采用当前普遍应用的航迹点表示方法,同时,为适应无人机飞控计算机算力,实时在线规划,牺牲一定程度的路径最优性,以保证算法计算效率。
1.1 坐标表示与变换
由于本研究中无人机航迹规划算法涉及点间距离角度以及向量运算,因此选择无人机导航制导常用的北东地坐标系(north-east-down,NED)作为当地坐标系进行表示和计算。在二维坐标条件下,不考虑高程,需将点的经纬度坐标转换为北向和东向坐标。为提高计算效率,本研究中采用等距方位投影[22]进行坐标变换。方位投影是地图投影的一种,其以平面作为投影面与地球表面相切或相割,并将球面上的经纬线投影至该平面所形成的一类投影。等距方位投影则是投影中心点至地图各点的距离和方位角不变,但存在角度变形和面积变形,介于等角和等积投影之间。由于等距方位投影中各点与中心点的距离和方位多是精确的,因此常被用作交通地图指导航空航海。
在等距方位投影中,选择NED坐标系原点作为投影中心点,令其经度和纬度分别为λ0和φ0,则对于纬度和经度分别为φ和λ任意一点在NED坐标系中投影坐标(x,y)为
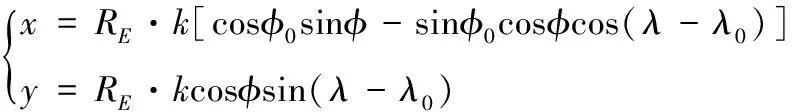
(1)
其中,RE=6371 km为地球平均半径。

(2)
cosc=sinφ0sinφ+cosφ0cosφcos(λ-λ0)
(3)
相反,将NED坐标系中的点变换至纬度和经度坐标则分别为

(4)
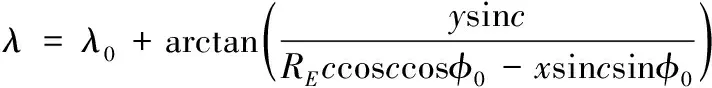
(5)
其中
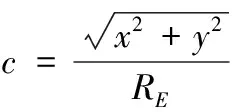
(6)
坐标变换计算中应注意经纬度单位的转换。
相比三维坐标变换,投影计算方法显然计算速度快效率高,同时也能将精度损失保持在可接受范围内,适于机载飞控算力。
1.2 障碍区域表示与处理
本研究中考虑的二维平面障碍区域采用多边形点集的形式,按顺时针或逆时针顺序进行表示,能够有效拟合不规则区域,并且易于以链表或数组等现有数据结构进行存储或通信。对于障碍区域的多边形点集表示需作如下假设。
假设1:区域间不存在重叠,即多个区域重叠则按一个连通障碍区域处理。
假设2:不同区域间的间隔距离应超过2倍于无人机转弯半径,小于该距离则按一个连通障碍区域处理。
2个假设是为了保证数据合理性和无人机飞行动力学条件下存在有效解。由于算法是基于几何关系设计,因此在数据预处理方面,对于多边形障碍区域,还需对凹多边形区域进行凸化处理,以保证规划航迹点满足要求,后文将进一步说明。
障碍区域的凸化处理采用凹点剔除方式。首先,对于多边形区域的点集中任意点,判断其是否在其余点所组成的多边形内,若该点位于其内,则该点为凹点须剔除,或者该点位于该多边形顶点或边上时,由于该点为重复或者多余的点也应剔除,反之则为凸点,应保留。遍历多边形障碍区域所有点重复该过程,直至该区域每个点均满足位于其余点所组成的多边形外,即均为凸点,从而使多边形障碍区域为凸多边形,完成区域的凸化处理。
由此,将多边形凸化处理过程转变为判断点是否在多边形内的问题。该判断方法采用射线法[23],由判断点引出一条任意方向射线,若与该区域其余点所形成多边形相交,且与各边交点总个数为奇数,则该点位于多边形内,否则,若射线与该多边形各边的交点总个数为偶数,则该点位于多边形外。射线法的优势在于可以采用垂直或水平射线,使判断过程简化直观。
凸化处理示意图如图1所示,选取多边形区域某个顶点P作为判断点,其垂直射线与其余各点所组成多边形区域相交情况如图1所示。
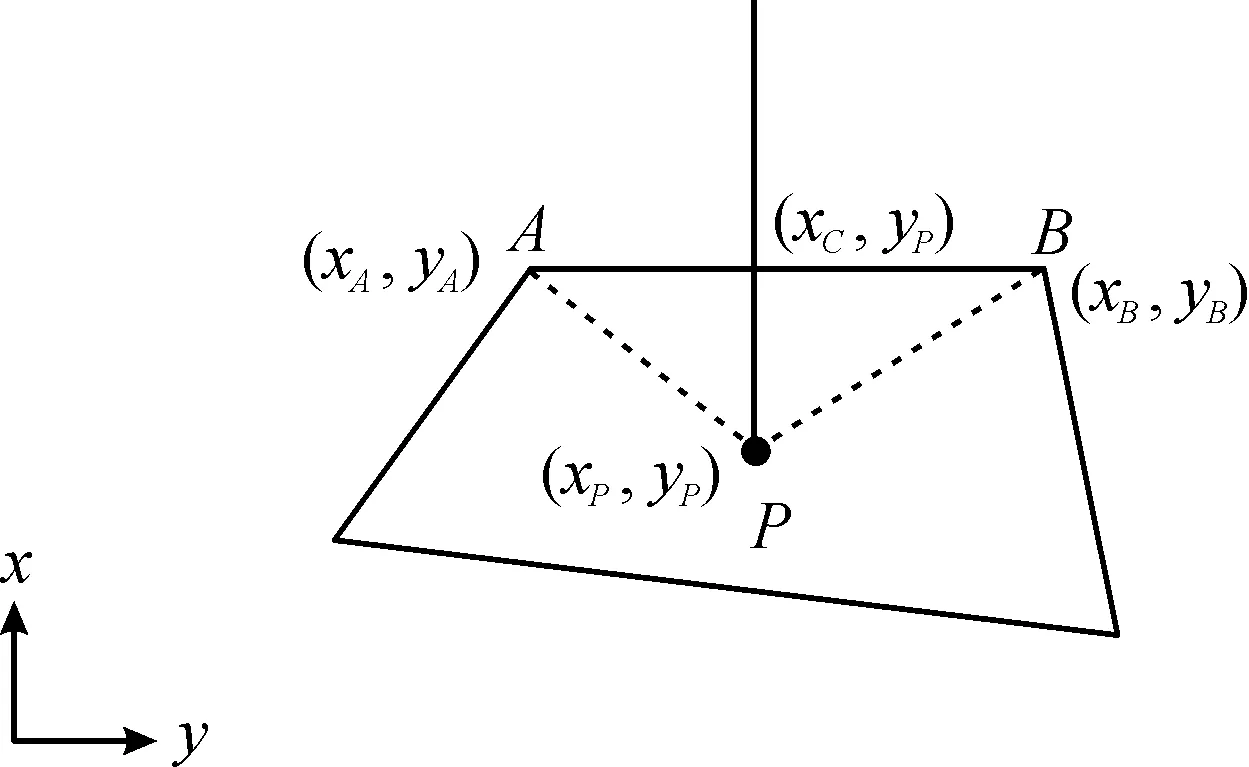
图1 凸化处理示意图
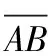
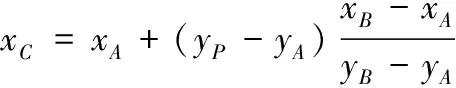
(7)
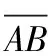
障碍区域凸化处理算法伪代码如下。
算法1:障碍区域凸化处理
输入:障碍区域点集pointsblock
输出:凸化处理后的障碍区域点集pointsblock
参数:点在内部标志位flagin,判断点pointP,其余点所组成多边形任意连续两顶点pointA和pointB,假想焦点xC
1:forpointPinpointsblockdo
2:flagin←False
3:foradjacent pointspointA,pointBexceptpointPinpointsblockdo
4:ifpointP==pointA||pointP==pointB||
5: (pointP.y==pointA.y&&pointP.y==pointB.y&&
6: (pointP.x-pointA.x)(pointP.x-pointB.x)≤0)then
7:flagin← True
8:break
9:endif
10:if(pointP.y>pointA.y&&pointP.y≤pointB.y) ||
11: (pointP.y>pointB.y&&pointP.y≤pointA.y&&
12: (pointP.x-pointA.x)(pointP.x-pointB.x) ≤ 0)then
14:ifxC==pointP.xthen
15:flagin←True
16:break
17:endif
18:ifxC>pointP.xthen
19:flagin← !flagin
20:endif
21:endif
22:endfor
23:ifflaginthen
24: removepointPfrompointsblock
25:endif
26:endfor
27:returnpointsblock
注意,经过凸化处理,障碍区域可能一定程度被扩大,对于极端情况下凹度较大的区域可能并不适用。
2 基于几何关系的航迹规划与避障
本研究中航迹点采用链表或数组数据形式进行存储,在给定起点和终点的条件下,航迹点初始包含起点和终点。由于任意2个连续航迹点间能够形成向量,因此基于几何关系在起点和终点间规划航迹点,从而对障碍区域进行规避。
2.1 避障判断与航迹点添加
对于经过凸化处理的多边形障碍区域,不考虑特殊情况,假设起点和终点均位于障碍区域外,且根据假设2以及设计算法能够保证规划添加的航迹点不位于任一障碍区域内,则若已存在两航迹点间向量被障碍区域阻截,则该障碍区域有且仅有2条边与该向量相交(不包括与向量重合的边)。由此,通过对阻截的障碍区域所相交的2条边进行延伸,延伸方向为所相交向量与多边形区域距离最远的顶点所在侧的相反方向,延伸距离为2倍规划对象机动半径,由此形成2个新航迹点,按照与该相交向量起始航迹点的距离从小至大顺序添加至向量2个航迹点之间,从而形成新的规划航迹,达到避障目的。
根据上文分析,障碍区域的避障问题转化为向量相交判断和延伸问题。由于主流编程语言对于向量操作均有较为丰富的方法库,且运行效率较高,因此,向量相交判断和延伸能够通过库函数进行实现,极大提高计算速度,由此提出基于几何关系的判断方法。
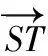
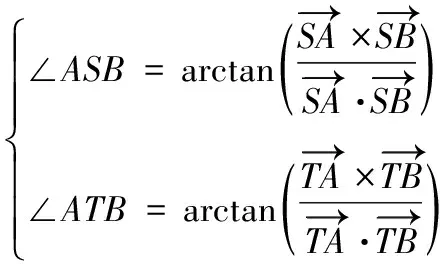
(8)
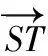
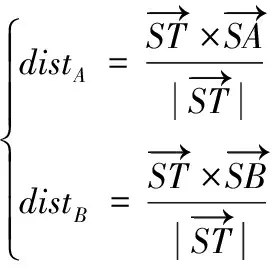
(9)
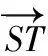
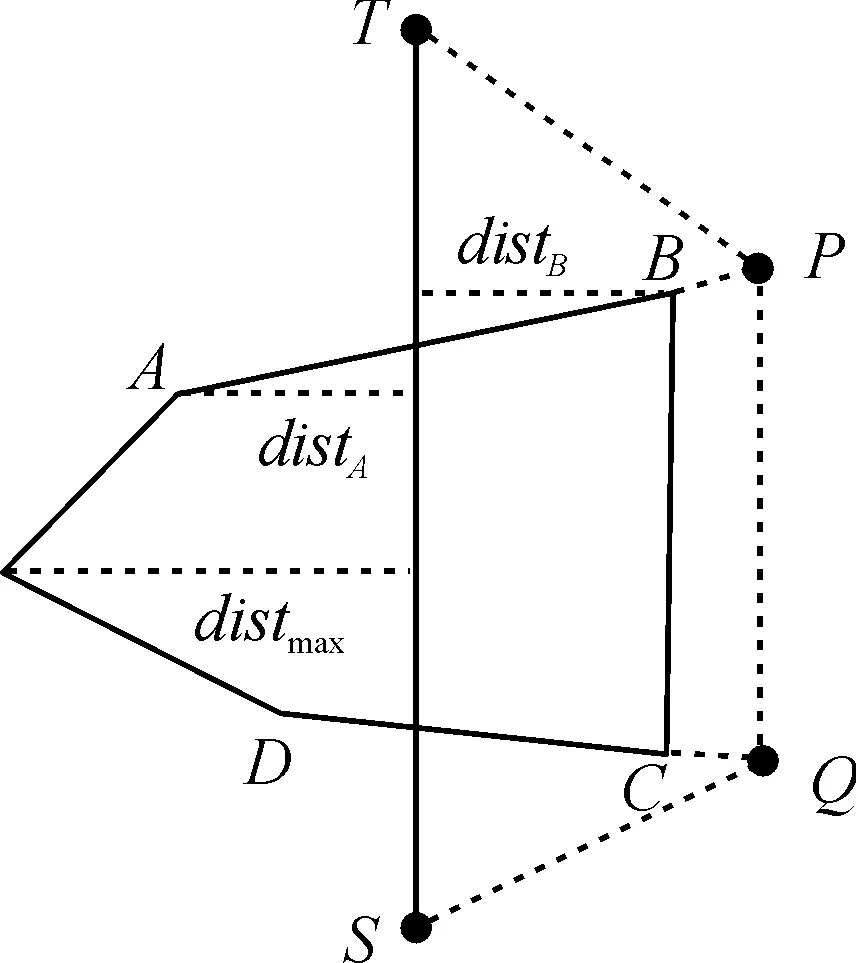
图2 避障航迹点添加示意图
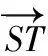
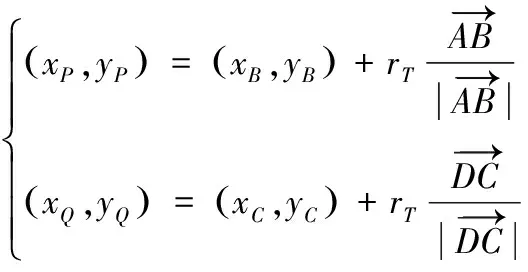
(10)
反之,则向点A和点D方向延伸形成

(11)
其中,rT为规划对象机动半径。而后,根据点P和点Q到点S的距离远近将2个新航迹点依次添加至航迹点S和点T中间,即S→Q→P→T。
避障判断与航迹点添加算法伪代码如下:
算法2:避障判断与航迹点添加
输入:2个连续航迹点pointS和pointT(链表形式),障碍区域点集pointblock
输出:处理后点S至点T的航迹点集(链表形式),航迹点添加标志位flagadd
参数:多边形任意连续两顶点point1和point2以及2点距航迹点向量的距离dist1、dist2和与航迹点向量的夹角θS、θT,多边形两条相交边的4个顶点pointA、pointB、pointC和pointD以及A点距航迹点向量距离distA,航迹添加点pointP和pointQ,二次相交标志位flagfirst,最大距离distmax,机动半径rT
1:flagadd←False
2:flagfirst←True
3:distmax← 0
4:foradjacent pointspointspoint1,point2inpointsblockdo
5:dist1← cross(vector(pointS,pointT),vector(pointS,point1))
6:dist2← cross(vector(pointS,pointT),vector(pointS,point2))
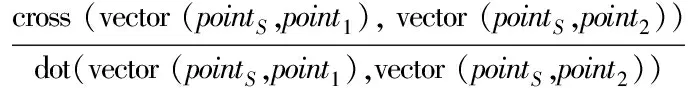
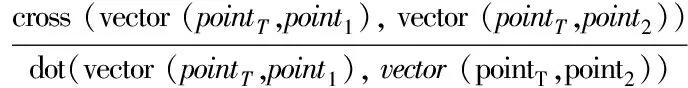
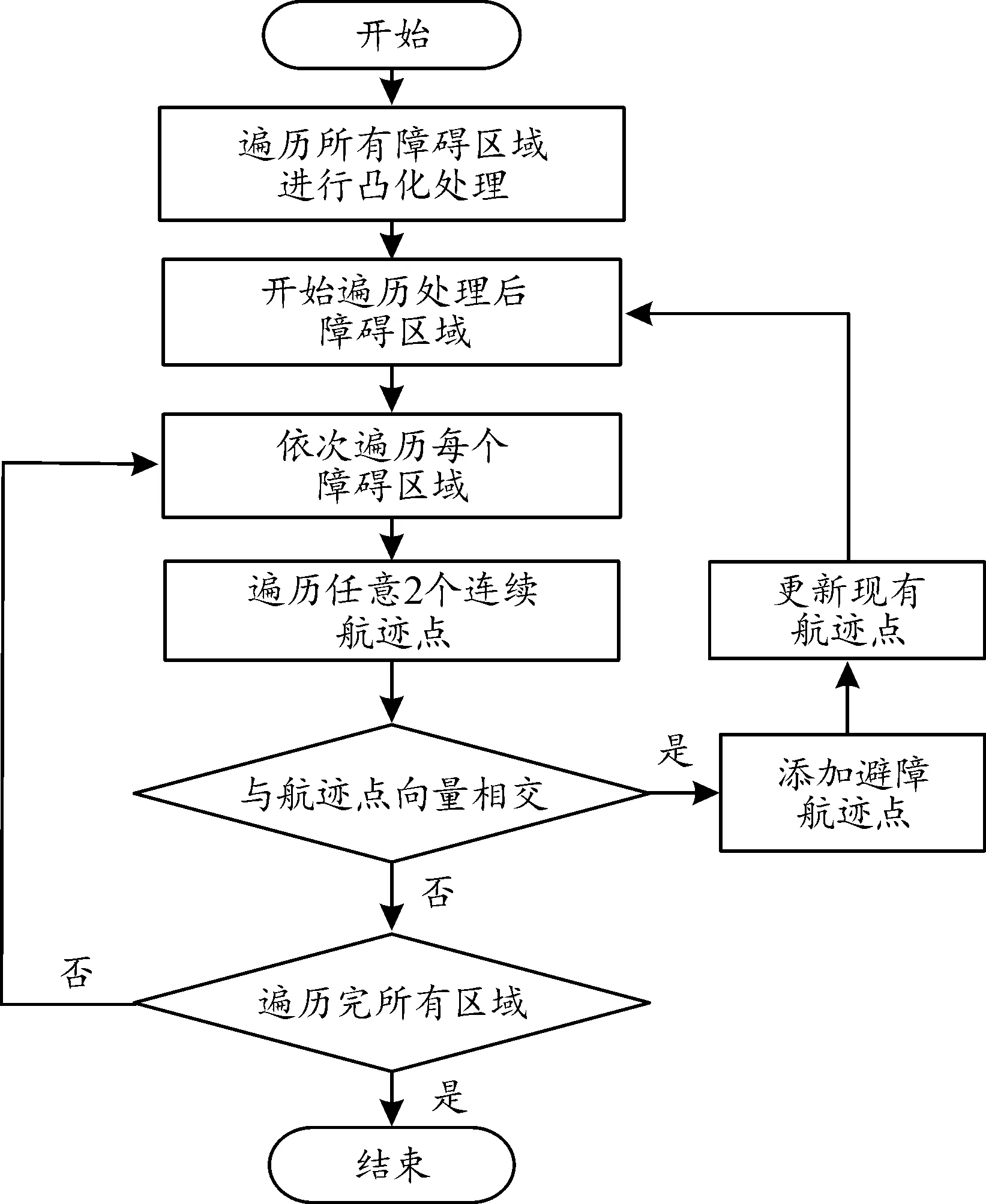
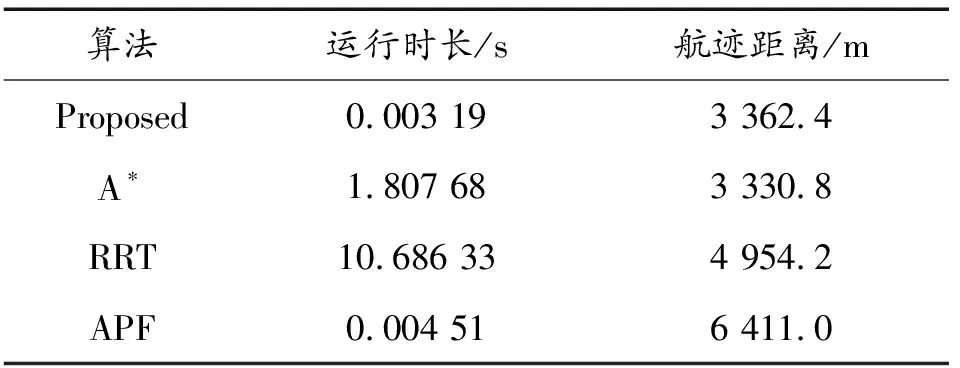
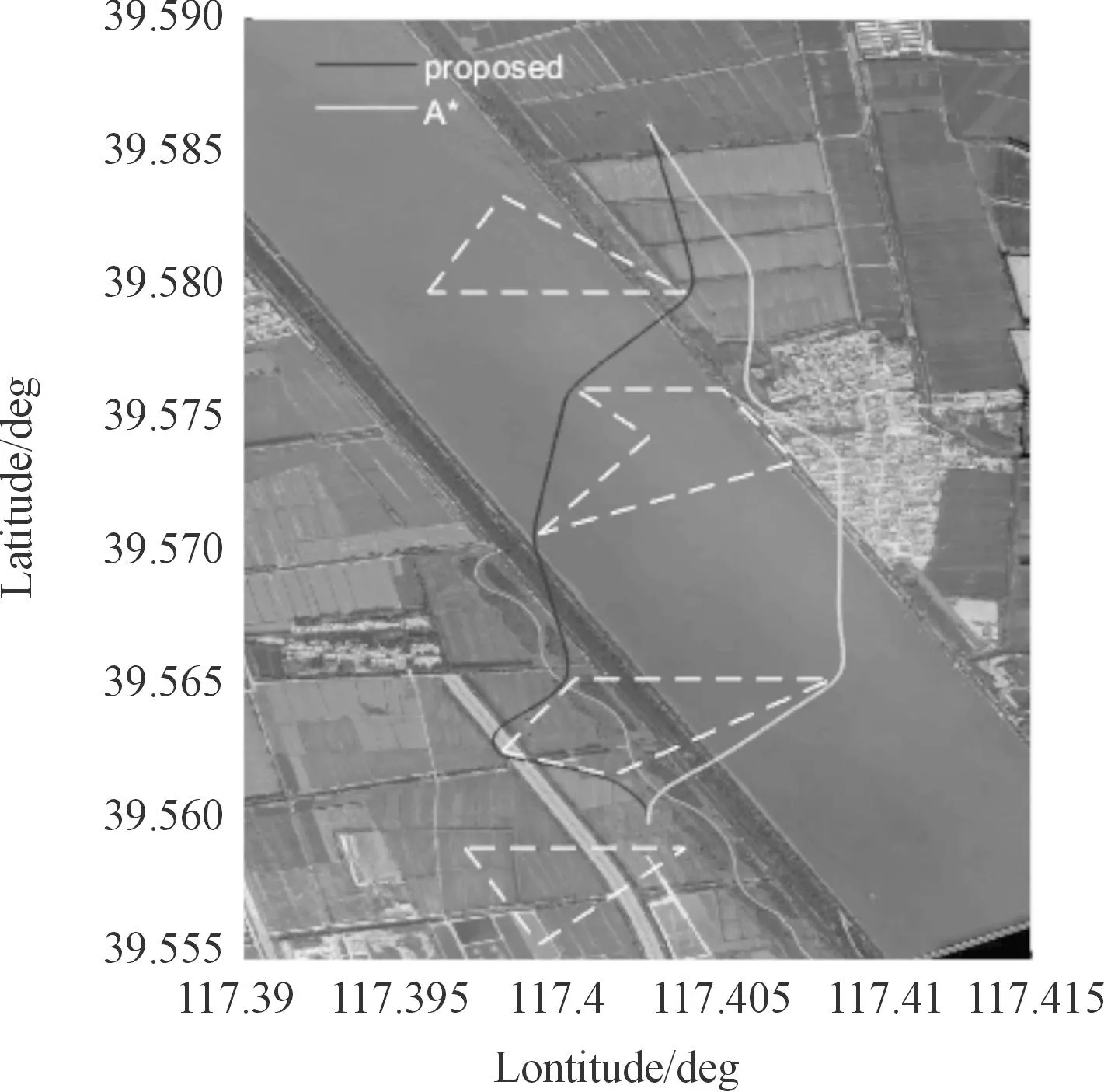
9:ifabs(distmax) 10:distmax←dist1 11:endif 12:ifabs(distmax) 13:distmax←dist2 14:endif 15:ifdist1·dist2≤ 0&&(dist1| |dist2)&&θSθT< 0then 16:ifflagfirstthen 17:flagadd← True 18:flagfirst← False 19:pointA←point1 20:pointB←point2 21:distA←dist1 28:else 22:pointC←point1 23:pointD←point2 24:endif 25:endif 26:endfor 27:ifflagaddthen 28:ifdistmax·distA≥ 0then 29:pointP←pointB+ 2rT· normalize(vector(pointA,pointB)) 30:pointQ←pointC+ 2rT· normalize(vector(pointD,pointC)) 29:else 31:pointP←pointA+ 2rT· normalize(vector(pointB,pointA)) 32:pointQ←pointD+ 2rT· normalize(vector(pointC,pointD)) 33:endif 34:ifnorm(vector(pointP,pointS))>norm(vector(pointQ,pointS))then 35:pointP↔pointQ 36:endif 37:pointS.next←pointP 38:pointP.next←pointQ 39:pointQ.next←pointT 40:endif 41:returnpointS,flagadd 由此,针对该障碍区域的避障航迹点添加完毕。由于起点和终点位于障碍区域外,且根据假设2,在给定延伸距离为转弯半径的条件下,保证了规划航迹点的可行性和有效性,避免了避障航迹点添加在障碍区域内或无人机在该点机动范围触碰临近障碍区域,因此无需对航迹点进行平滑处理。同时,通过判断障碍区域所有点与相交航迹向量的最大距离,进行避障航迹点反向延伸添加,实现了无人机针对该障碍区域的最短路径避障。 根据上文算法设计,通过几何关系添加避障航迹点的方式完成了对单个多边形障碍区域避障。因而,针对所有需考虑的障碍区域,按照上述方法对每一个区域遍历处理,对于与已规划航迹点相交的任何一个障碍区域,添加避障航迹点后,需对所有区域重新遍历,以确保区域的遍历处理顺序不对结果产生影响,即所规划航迹点能够避开所有区域,从而完成对所有障碍区域的避障。算法整体流程如图3所示。 根据上述算法流程,针对所有障碍区域生成全局航迹点。值得注意的是,对于所有障碍区域的重复遍历判断,虽然在一定程度上降低了计算效率,但相比基于离散地图的搜索方式,基于几何关系的计算方法仍能极大减小算法计算时间,同时,重复遍历也确保了障碍区域能够实时添加,在前序航迹规划基础上动态计算。相对不足的是,由于没有在全局进行优化,仅针对单个区域考虑最优避障路径,该方法仅能够得到次优解,若从最优化方面而言,对该航迹规划方法选择应有所取舍。 图3 算法整体流程图 为验证算法性能,首先通过数值仿真对算法进行测试分析与对比。本研究中选择A*算法、快速扩展随机树法(rapidly exploring random tree,RRT)、人工势场法(artificial potential field,APF)作为对比方法,A*算法应用广泛,且对于静态规划效果较好,RRT基于全局地图采样,能够很好处理带有非完整约束的路径规划问题,APF作为动态规划方法,工程应用广泛,因此3类对比方法具有普遍性,能够作为参考验证算法性能。A*算法采用8朝向移动,为避免与障碍区域碰撞,同时保证可操作性,直线移动距离同样定为2倍转弯半径,斜线移动按对角距离处理,启发函数采用欧式距离;RRT算法对全局地图对东西南北各向拓展0.5倍起点至终点距离,并采用2倍转弯半径进行采样;APF算法引力势场Vs和斥力势场Vc设计如下 (12) (13) 通常在无人机飞控系统中,速度和高度控制采用TECS方法,水平航迹跟踪采用L1算法,因此无法直接接收速度指令,APF算法通过向期望速度方向延伸2倍转弯半径形成航迹点方式进行航迹规划计算为 (14) 数值仿真选择当地坐标系即NED系下进行,起点和终点的水平坐标分别为(0,0)和(2 900,0),障碍区域设置如表3所示,无人机转弯半径设为10 m。数值仿真计算的硬件环境基于Intel i9-9880H的CPU和16 G的DDR4内存,软件语言基于C++编写运行。 表3 障碍区域设置 数值仿真对比结果如图4所示,4种方法的航迹规划都成功避开了障碍区域,但路径选择有区别。算法计算结果如表4所示,包括运行时长和规划航迹距离。根据图4和表4,所提出算法大幅降低了计算时间,达到了毫秒级,与A*算法相比虽然不能保证最优性,但基本处于同等优化水平,并且不需要地图栅格化表示。相较而言,A*算法计算时间较长,RRT由于随机采样不仅计算时间过长也无法保证规划航迹最优性,每次计算时间和航迹均有较大差异,APF算法计算时间同样达到了毫秒级,但由于规划航迹在障碍区域边界振荡,显示的航迹距离较大,因此需要对规划航迹进行平滑。由此可见,所提出算法既达到了较高的计算效率,同时也保证了优化水平,不需要平滑规划航迹,并且完全能够适用于无人机飞控算力,具备可行性。 图4 数值仿真对比结果 表4 算法计算结果 根据数值仿真结果,在此基础上开展飞行试验,以进一步验证算法性能。由于RRT算法运行时间和规划航迹均具有不确定性,APF算法对参数较为敏感,且需要航迹平滑,不具有可靠性,因此飞行试验仅采用A*算法作为对比。飞行试验平台选型如图5所示,选择FMS塞斯纳EPO泡沫机作为算法测试无人机,硬件选择HolybroPixhawk4开源飞控,软件选用PX4v1.11.0版本。该开源飞控平台基于ARMCortex-M7体系架构处理器STM32F765进行运算,算力充足,并且PX4飞控软件采用Nuttx操作系统进行任务调度,而航迹规划算法在实际飞行中运行频率较低,因此所提出算法能够移植于该飞控系统。 将所提出算法按照PX4中标准任务模块改写,在头文件中声明所需变量和类的实现方法,并在系统CMakeLists中进行添加。障碍区域坐标信息通过自定义MAVLink消息实现,每个障碍区域独立打包,在地面站实时上传,飞控系统通过任务程序进行接收。该任务程序选择位置控制模式作为控制变量,由地面站更改该变量值进行激活,激活后无人机按照当前坐标定点盘旋,当地面站更改位置控制模式为自动寻迹模式后,任务程序根据接收到的障碍区域运行更新函数规划航迹,并通过PX4系统uORB发布,无人机将按发布航迹点进行飞行,寻迹飞行过程中仍可通过更改控制变量激活航迹规划任务程序,上传新的障碍区域。 图5 飞行试验平台选型 飞行试验的障碍区域设置与数值仿真保持一致,以保证天地一致性。飞行开始前仅设定起始点和目标点,障碍区域点均采用经纬高形式上传。飞行开始后,通过地面站激活飞控系统任务程序,实时上传4个障碍区域后,更改控制变量为自动寻迹模式,无人机将在航迹规划完成后由盘旋转为按规划航迹点飞行。由于A*算法为静态规划算法,计算时间较长,无法在飞控系统中移植,A*算法的飞行试验仅将离线规划的航迹点在飞行开始前完成上传。飞行试验中,测试无人机飞行速度设定为15 m/s,飞行高度为70 m,航迹点接受半径为50 m。 飞行试验对比结果如图6所示。测试无人机按照所提出算法与A*算法的规划航迹飞行,均能够实现避障,满足性能要求。由于所提出算法的规划航迹转弯方向较大,飞行轨迹离障碍区域较近,但由于考虑了无人机转弯半径,因而仍能够避开障碍区域。 图6 飞行试验对比结果 从起始点至目标点,所提出算法飞行总用时为217.4 s,A*算法飞行总用时为210.4 s。可见,由于无人机转弯影响,所提出算法规划航迹的最优性在实现上有一定损失,而A*算法的8朝向则更易实现。但是,所提出算法基于实时上传的障碍区域在线规划动态计算,达到了实时性和快速性的目的。由此,通过飞行试验对所提出算法性能进行了验证,算法满足可行性和有效性要求,具有较快运行速度和较高计算效率,能够移植于现有飞控系统。 针对无人机二维区域避障提出了一种基于几何关系的航迹规划方法,并通过数值仿真和飞行试验对其性能进行了对比分析和验证。研究表明: 1) 所提出方法基于几何关系进行航迹规划,避免了全局地图离散化表示,规划时间远小于其他类型规划算法,并且具有较高规划水平,能够适用于现有飞控算力,并可靠移植于现有飞控系统; 2) 所提出方法相比静态规划类型算法,能够根据实时上传的障碍区域在线规划动态计算,满足了实时性和快速性要求; 3) 所提出方法规划航迹考虑了无人机转弯半径,经过飞行试验验证,能够避免无人机机动范围触碰障碍区域,满足了有效性和可行性要求。2.2 全局航迹生成
3 仿真与验证
3.1 数值仿真
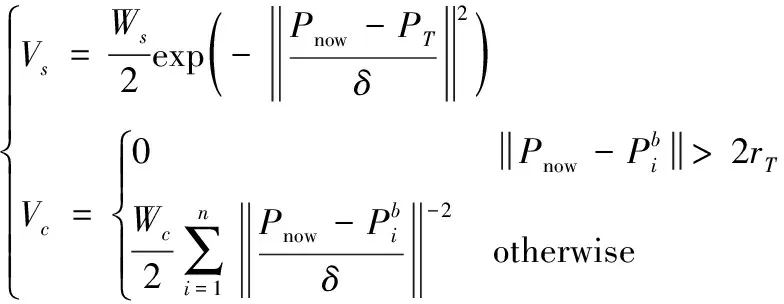
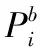
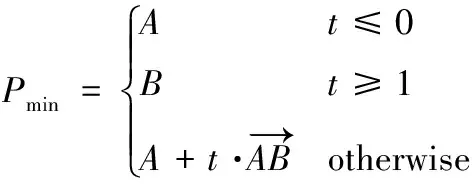
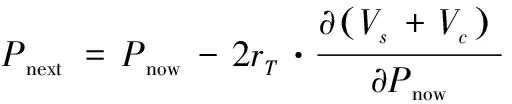
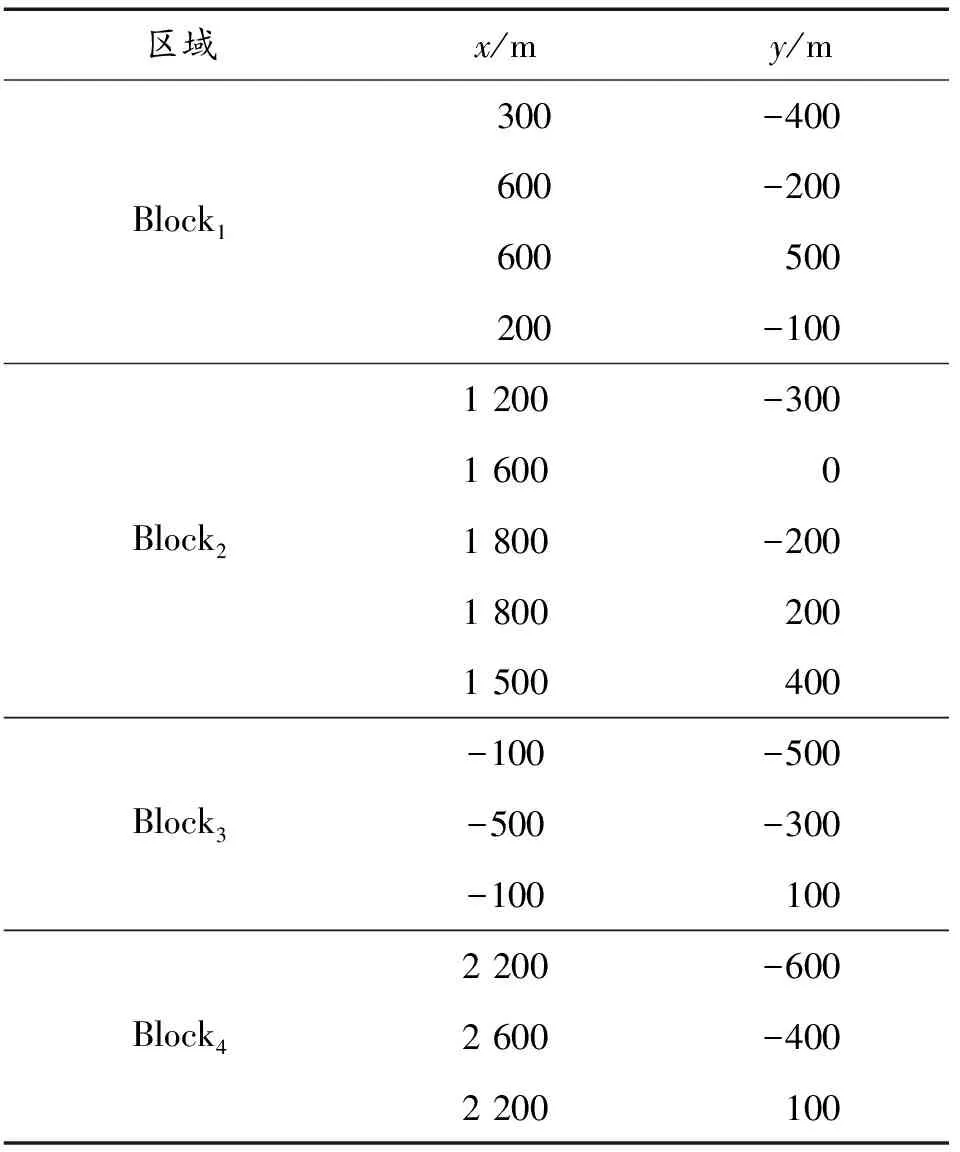
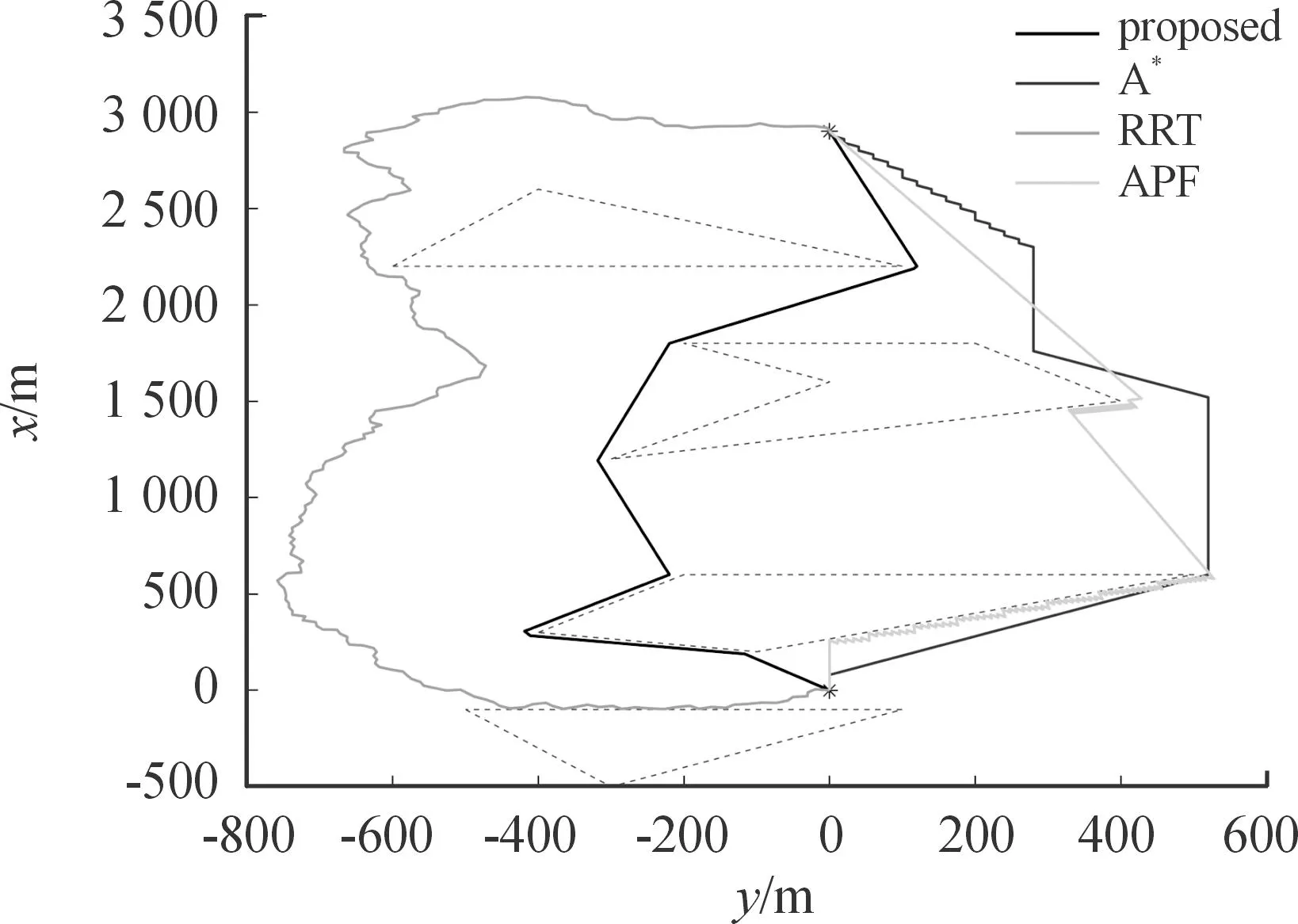
3.2 飞行试验

4 结论

