基于数字地形平滑和人工势场的无人机近地三维路径规划

朱 熠,田 辉,郝向宇,史涵意,马文峰,王 聪

(陆军工程大学 野战工程学院, 南京 210007)

0 引言

通常来说,路径规划的目的是生成一条最快、最简单的路径,摆脱复杂地形、障碍物和威胁源等所有不利因素[1-3]。然而,当无人机在近地区域飞行时,由于飞行任务可能对地形有所限制和要求,如地形跟随(terrain following,TF)和地形回避(terrain avoidance,TA)。因此,威胁因素仍在考虑之中,此时三维路径规划的任务就变得艰巨而富有挑战性。

在处理近地区域三维路径规划问题时,首先需要一个数字地形模型。以前,地形模型通常由路径设计者自己创建,现在有许多真实地图的数字模型可用。例如,航天飞机地貌雷达任务(shuttle radar topography mission,SRTM)模型是最常用的模型之一[4-6],其所有数据覆盖了地球80%以上的陆地表面[7-8]。通过对SRTM地形数据进行一些轻微的转换,可以使用Matlab软件进行编辑和处理[9-10]。通过地形平滑方法,可以生成安全飞行曲面。不少文献通过对飞行轨迹的优化,以满足飞机的机动性和地形跟随的要求[11-12]。

在通过地形平滑生成安全飞行曲面后,可以通过搜索算法获得最优飞行路径。关于无人机路径规划算法大多是基于搜索算法的改进和评估指标的优化[13-14]。本文中提出一种基于数字地形平滑和人工势场法的三维路径规划方法,该方法将地形平滑技术和向量场搜索相结合。仿真结果表明,所设计的方法可以在安全飞行曲面上获得最优的三维路径。

1 数字地形平滑

1.1 数字地形模型

为获得数字地形模型,采用SRTM数字高程模型。下载SRTM的59_06地形数据,如图1(a)所示。由于原始59_06地形非常大,因此只选择了其中的一小部分,如图1(b)所示。

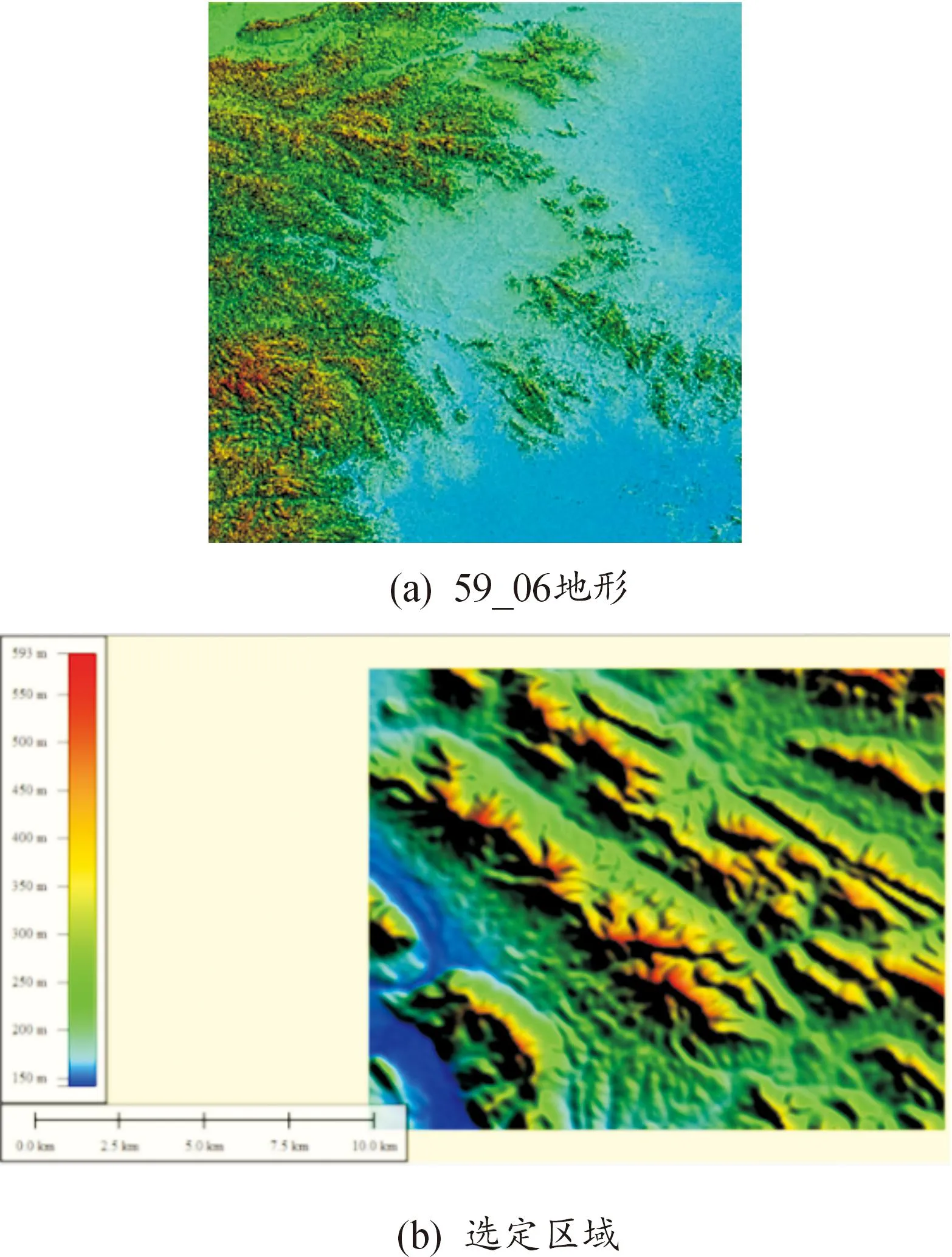
图1 59_06地形数据和所选定区域

使用Global Mapper或Surfer软件可以方便地编辑SRTM地形数据。通过Surfer,SRTM地形数据可以从.grd格式转换为.dat格式,.dat格式的文件可以在Matlab软件中进行编辑。

1.2 地形平滑处理

无人机的飞行状态会受到其机动性能的影响,这些性能主要包括最大爬升角、最小转弯半径、最大机动过载、飞行速度和飞行高度的限制。通过平滑地形模型并生成安全飞行面可以满足无人机机动性能的这些要求。在本节中,提出了设置地面以上安全高度、减小坡度和减小曲率的设计思路。

1) 设置高于地面的安全高度。地面的隐蔽要求和防撞要求之间存在矛盾。为了实现平衡,设置了地面以上的最低安全高度。当无人机飞得高于安全高度时,飞机可以避免撞到地面。在飞行高度高于安全高度的情况下,无人机可以最大限度地降低航迹的高度。在不同的地形中,最低安全海拔是不同的:在海洋和平原地区,安全海拔较低;而在丘陵和山区,安全海拔较高。一般情况下,适宜的安全海拔为:15～30 m的海域、60～80 m的平原区和约120 m的丘陵区。

2) 降低坡度。在低空突防任务中,无人机有一个最大爬升角的限制。如果前方有坡度大于最大爬升角的山峰或障碍物,无人机需要提前爬升。否则,将导致与山体或障碍物发生碰撞。因此,需要对坡度较大的地形进行修改,以满足无人机纵向飞行的约束。坡度约束由无人机的最大爬升角决定。最常用的方法是用无人机的最大爬升角代替原始地形的最大坡度。坡度降低方法如图2所示。

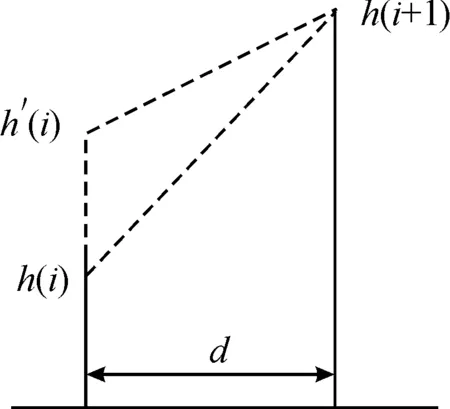
图2 减小坡度

图2中,i为描述高度信息的离散网格点,h(i)为对应的高程值,d为网格间距。记坡度为k=(h(i+1)-h(i))/d,最大可飞坡度为kmax,坡度处理逻辑为:

ifk>kmax,h(i)=h(i+1)-d·kmax,

i=1,…,n

else ifk<-kmax,h(i+1)=h(i)-l·kmax

elseh(i)=h(i),h(i+1)=h(i+1)

上述逻辑只考虑了相邻2个点之间的坡度问题,没有考虑坡度的整体变化趋势,需要多次迭代才能得到理想的效果,甚至可能会出现峰巅相互拉高而不收敛的现象。

综合来说主要的改进思路包括2个方面:

① 以最高山峰点为起点,依次对其两侧地形坡度进行处理。首先寻找每行每列最高的山峰,标记它们的位置;然后从最高山峰开始分别从正向和负向2个方向进行坡度约束处理。

② 对山峰进行保护,对小于最大可飞坡度的山峰尽量少做处理。

采用上述改进逻辑,可以提高程序处理的速度,山峰不会互相削平或者相互拔高。

3) 降低曲率。无人机在铅垂平面内运动轨迹的曲率ρa和法向加速度nz的关系为

(1)

根据无人机的速度和最大法向加速度计算出地形曲率的最大值ρamax,然后对地形的曲率ρx、ρy进行约束处理,使它们的绝对值小于ρamax。由于相互正交的x和y方向的处理方法相同,下面只介绍x方向的处理方法。

设地形高程函数为h=h(x,y),则曲率ρx为

(2)

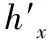
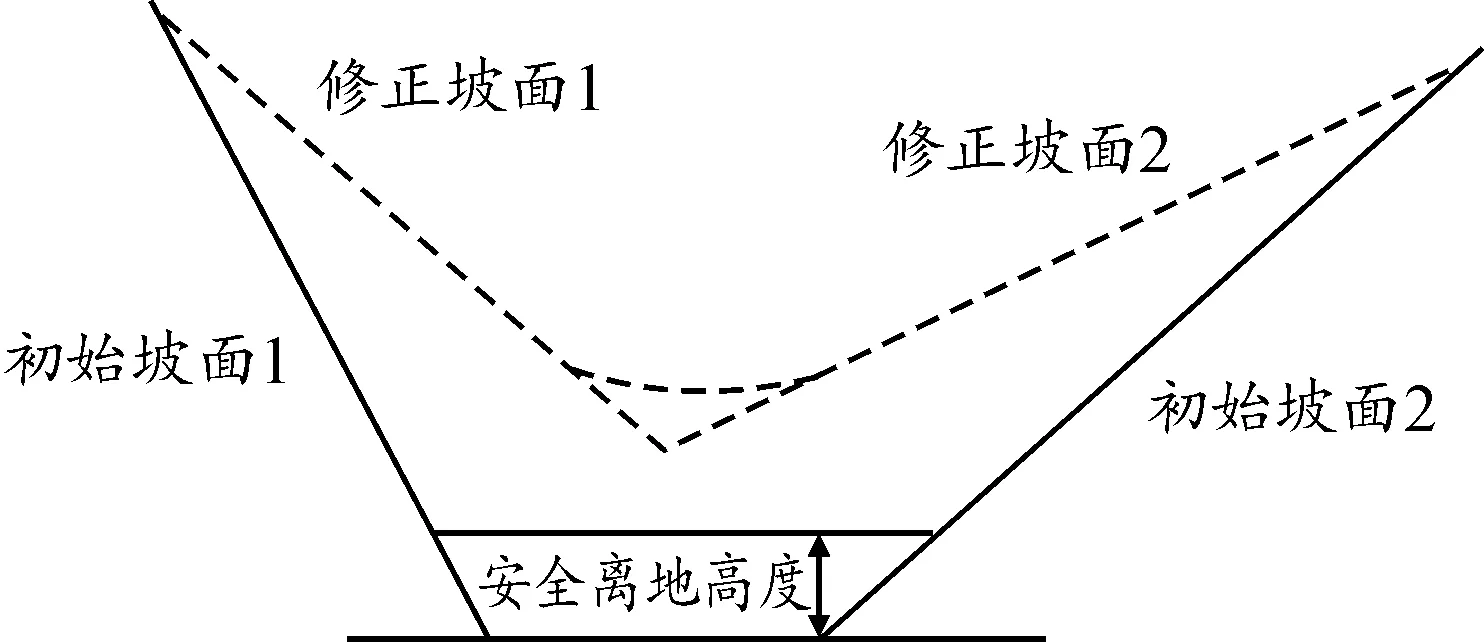
图3 地形曲率约束处理

为求栅格点的曲率必须已知其一阶偏导数和二阶偏导数。利用离散数据求近似偏导数的方法较多。考虑到在实时轨迹优化时,采用3次卷积插值算法对数字地形进行内插。用上述方法内插出的地形来求栅格点的一阶偏导数和二阶偏导数,然后求出栅格点的曲率。曲率约束处理采用与坡度约束处理同样的逻辑,具体步骤如下:

步骤1在坡度约束处理完成的基础上,从最高山峰点两侧分别开始进行曲率约束处理;

步骤2网格点(xi,yj)的一阶偏导数为

h′x=(hi+1, j-hi-1, j)/2l

(3)

由于3次卷积插值在栅格点处的二阶偏导数不连续,因此网格点(xi,yj)处的二阶偏导数需要分左右2种情况来求。网格点(xi,yj)处的二阶右偏导数为

h″xr=(2hi-1, j-5hi, j+4hi+1, j-hi+2, j)/l2

(4)

网格点(xi,yj)处的二阶左偏导数须利用网格点(xi-1,yj)处展开的插值公式求得,表达式为

h″xl=(-hi-2, j+4hi-1, j-5hi, j+2hi+1, j)/l2

(5)

把式(3)代入式(5)中可得网格点处的左右曲率。

步骤3网格曲率约束的处理会改变原来已进行过坡度修正的地形,因而每次计算网格曲率之前都要进行网格坡度的重新判断和调整;

步骤4措施3已确保了地形坡度约束是满足的,因而山峰和山谷之间的网格点是不需要进行曲率修正的,曲率的约束处理只存在于山峰和山谷。为了对山峰进行保护,山峰和山谷须分别设计处理方法。

1.3 安全飞行曲面生成

在本节中,在Matlab中分析了SRTM高程地形模型。Matlab中的“load”函数可用于读取SRTM的.dat文件,该文件已转换为包含经度、纬度和高度分量的三维矢量。“网格”函数用于展开平面中的点。插值函数“gridata”用于完成高度方向上的点。然后可以在Matlab中使用“网格”函数生成数字地形。“contour3”函数可用于生成等高线,如图4(a)和图4(b)所示。

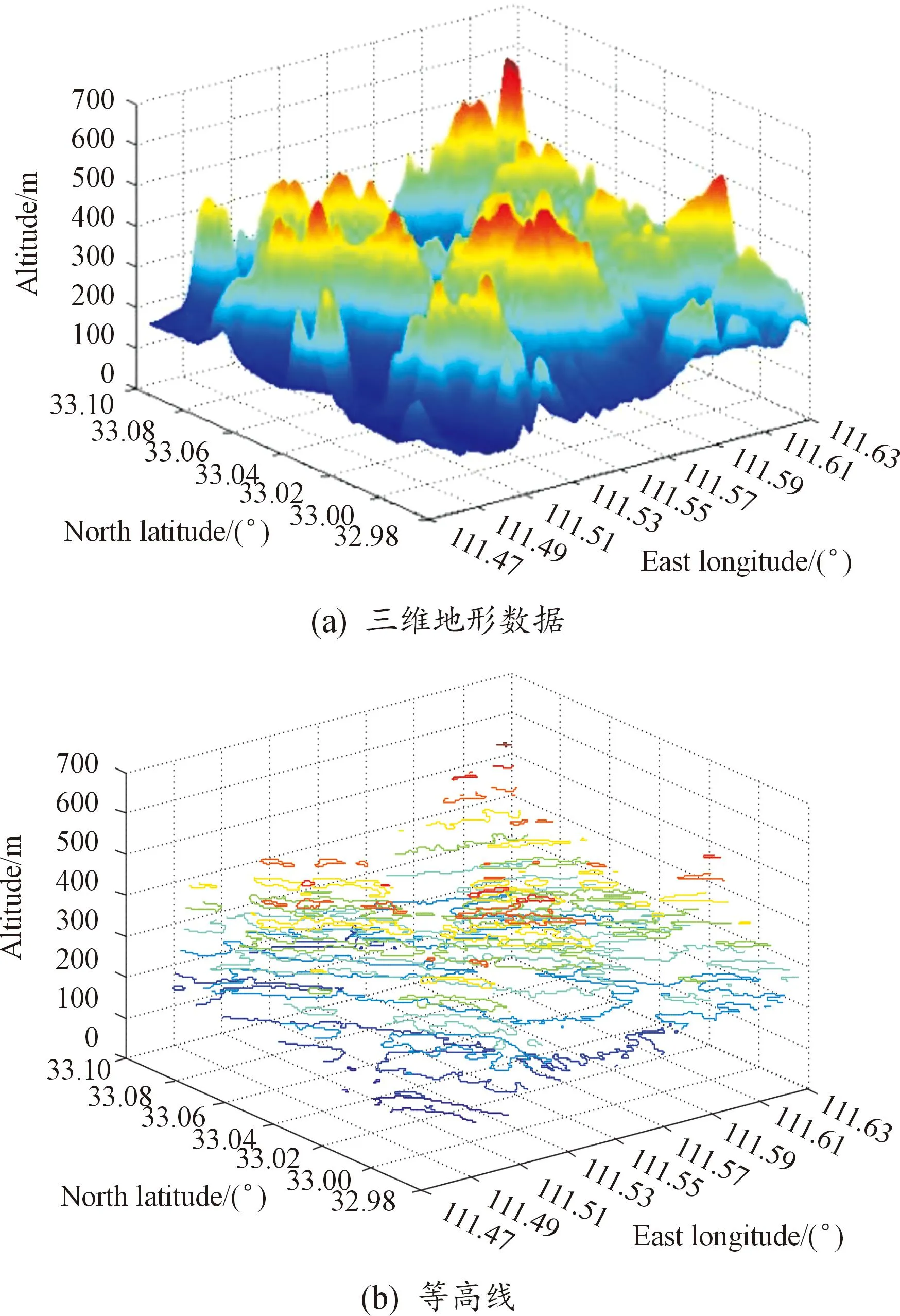
图4 地形数据的等高线

然后,上述方法可以用于平滑数字地形,主要考虑的因素是海拔、坡度和曲率的安全系数。平滑的结果如图5所示。

通过比较图5和图4(a),可以看到地形平滑的结果,即生成的安全飞行曲面。可见,总体趋势是完全保留的,最低高度提高了约150 m,最高山峰的高度保持不变,相邻的陡峭山峰平滑地连接在一起,因此为了安全飞行,坡度和曲率都减小了。

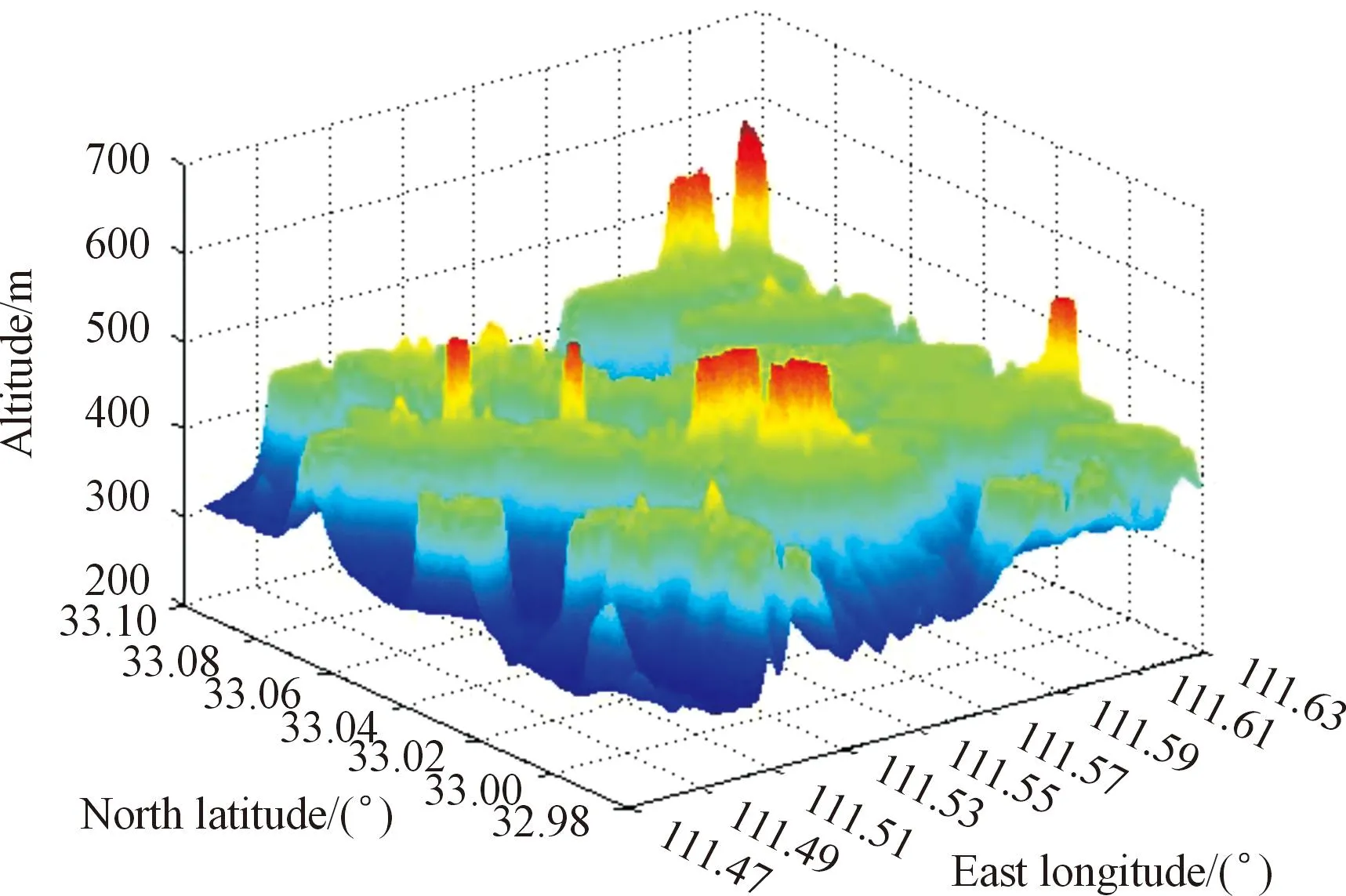
图5 平滑处理后的安全飞行曲面

2 三维最优路径规划

2.1 机动性约束指标

基于战术运用和飞行器性能的要求,无人机的机动性约束一般情况下包括以下5点:

1) 最短直飞距离:即飞行器在姿态改变前必须保持的最短直飞距离,设航迹由{Li|i=1,2,…,n}组成,最短直飞距离为Lmin,该约束可表示为

Li>Lmin(i=1,…,n)

(6)

2) 最小转弯半径:描述的是无人机过载约束的能力,在转弯过程中不考虑切向加速度因素,则有:

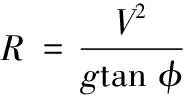
(7)

式(7)中:R为转弯半径,V为无人机飞行速度,φ为滚转角。

由于无人机有最小飞行速度Vmin,而且有最大滚转角φmax限制,所以R有最小限制,当规划的航迹的曲率大于该曲率时,无人机受最大过载限制将不能准确跟踪航迹飞行。因此,路径的曲率半径必须大于无人机最小转弯半径。即约束表达式如下:

(8)

3) 最大爬升/俯冲角:最大爬升/俯冲角的限制是产生的航迹在飞行控制系统能够允许的最大爬升/俯冲角内。假设最大爬升/俯冲角为γmax,该约束可以这样表示:

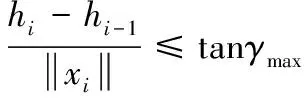
(9)

4) 最大飞行路径:对于燃油和飞行时间的限制,飞行路径的总长度必须小于预设的最大距离。将飞行路径的最大长度设置为Lmax,这样该约束可以表示为

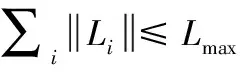
(10)

5) 目标进入方向:对于困难任务的要求,有时无人机需要从某个方向接近目标。这就是进入方向的约束。

2.2 威胁评估指标

飞行路径规划的评估指标设计为以下2种:

1) 代价指标

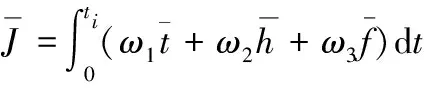
(11)

2) 威胁指标

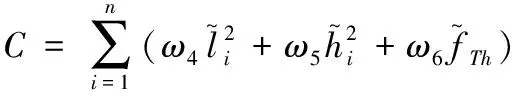
(12)

(13)

式(13)中:Kj为第j个威胁源的强度,Rsj为飞行器距第j个威胁源的斜距,Nt为已知威胁的个数。

2.3 最优路径搜索算法

航迹生成的原理分成2步:首先在xy平面内用路径搜索算法规划出能够规避威胁的最优二维路径;然后根据第1节所得地形平滑后的安全曲面,扩展出三维航路。故本节重点介绍xy平面内的路径搜索算法。

1) 算法描述。算法采用人工势场法的基本思想,其基本原理就是对所处障碍环境中每一点都赋一个势场值,其值是目标点的引力和障碍点的斥力叠加之和。因此路径规划也就是从起始点沿着势场下降最快的方向到达目标点。

将威胁源看成“规避场”,即每一个威胁障碍的位置原点都看作在产生一个排斥性的斥力场作用在即将路过的无人机上面。产生的斥力大小与它们之间距离的平方成反比,平面内任意一点受到第i个威胁障碍的斥力计算公式为

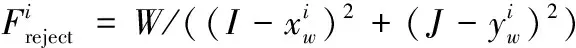
(14)

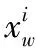
对于路径的目标点同样规划一个场,这是一个吸引力场,吸引力的大小正比于无人机和目标的距离,其计算公式为

(15)

式(15)中:xaim、yaim为目标点的位置坐标。这个力同样对平面中的点生成表格,是一张二维引力表。设当无人机处于初始位置时,引力达到最大值;当无人机运行到目标点时,引力达到最小值。这样的一个10×10网格点的引力表格如表2所示,表中数值为900的是无人机初始位置即引力最大的点,数值为300的是目标位置即引力最小的点。

2) 搜索过程。对斥力表和引力表进行合成,可以生成一张合力表,通过合力引导无人机运行出最优轨迹。具体步骤如下:

步骤1将整个平面区域离散化成100×100的网格地图,然后从第一个网格点P1,1开始,选取一个3×3的子图,共包含9个网格元素;

步骤2计算这个3×3的子图中的9个元素相互之间的受力值,选出所受合力最小的网格点;

步骤3进行解的摄动操作,即以步骤2中所得的合力最小网格点为中心,重新选取一个3×3的子图;

步骤4比较当前最小网格点的坐标与目标点是否相等,如果相等则终止程序,否则继续程序;

步骤5重复步骤2—步骤4直到完成所有100×100网格点。

3) 局部最优的处理。如果在第2)步搜索过程中无人机进入了一个区域,算出的当前最小合力网格点与上一步得出的网格点相同,而且这个点不是目标点,则搜索算法进入了一个局部最优循环中。

处理这个局部最优循环的方法是在这个点的位置增加一个高能量的威胁场,然后重新开始第2)步,这样无人机就会避开这个区域。

表1 10×10网格点的单个威胁场斥力表

表2 10×10网格点的目标点引力表

3 三维路径规划仿真

根据上节描述的路径搜索算法,并参考文献[15]中的仿真框架设计思路,采用Matlab软件设计了GUI(graphical user interface,图形用户界面)程序,优化了程序界面布局和回调函数中的搜索算法,改进后的程序能够直接导入1.3节生成的平滑后的安全飞行曲面。其中相关控件的名称和功能如表3所示。

表3 仿真界面中各控件功能说明

平滑后的数字地形及其等高线就显示在坐标轴系1和坐标轴系2中。在表3中所有控件的回调函数都已编码之后,GUI程序就设计完成了。

路径规划结果分4个步骤如下:

步骤1加载地图。“载入地形”按钮是指加载平滑处理后的三维地形的地图,如图6所示,即包括平滑处理后的安全飞行曲面及其相应的等高线。在图6中,3D地形的轴的单位由之前的纬度(°)、经度(°)和米(m)转换而来。

图6 在GUI界面中载入三维平滑地形

步骤2添加新威胁。点击界面中的“新增威胁障碍”按钮,即可添加威胁源。在等高线的任意位置左键单击1次,再单击鼠标右键即可完成一处威胁源的添加,柱状威胁源将出现在三维地形和等高线中。在任意位置先后随机设置5个威胁源后,得到如图7中所示的5排柱形威胁源。

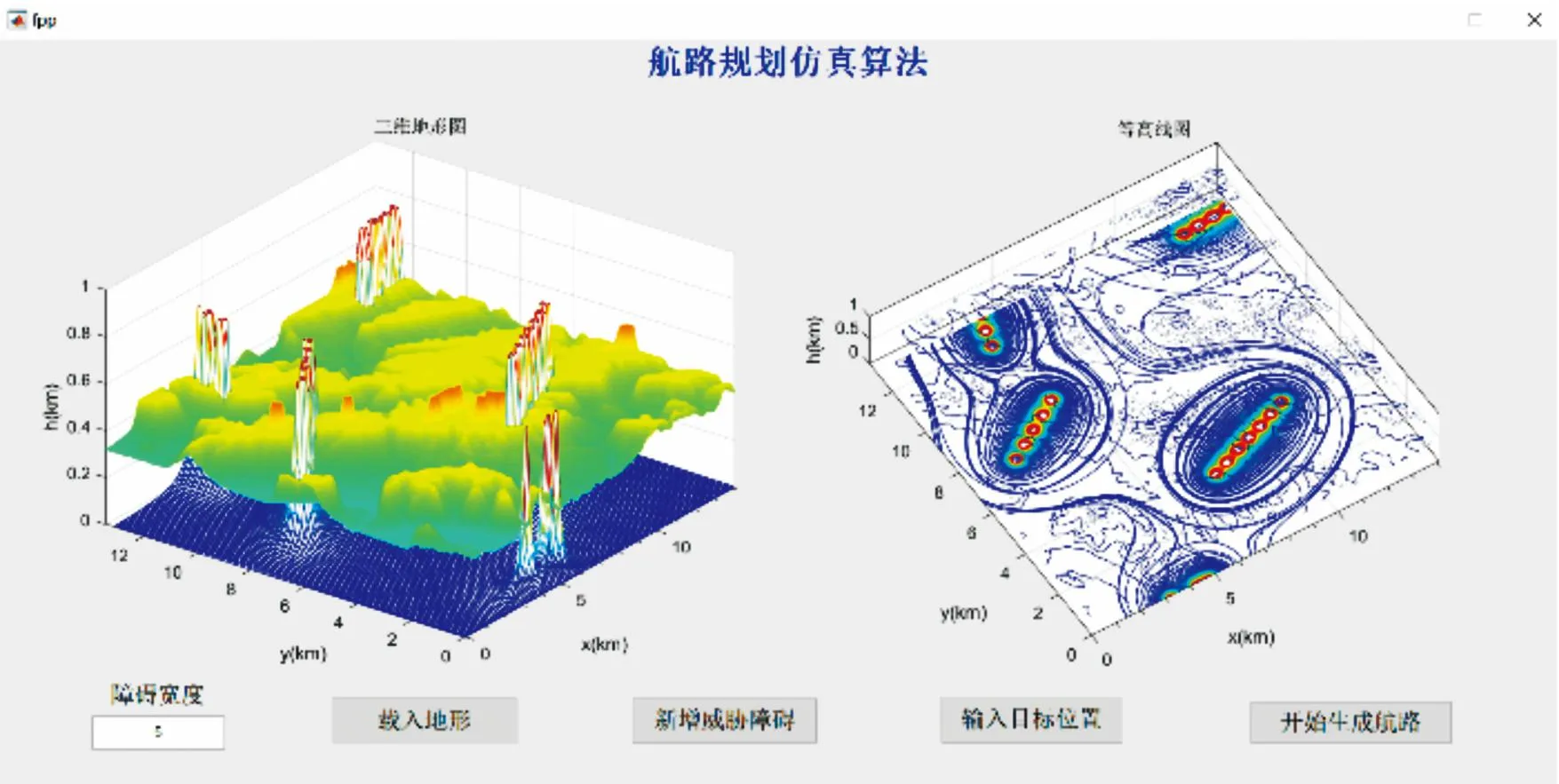
图7 设置威胁障碍

步骤3确定目标点。点击界面中的“输入目标位置”按钮。然后左键单击等高线图中威胁屏障外的任何位置,就会显示一个红色的小圆圈作为标记。

步骤4开始搜索。点击界面中的“开始生成航路”按钮。程序开始运行,依电脑计算性能不同,等待约1～2 s后,最佳飞行路径就出现在3D地形图和等高线图中,如图8(a)所示。

在图8(a)中,在右侧的等高线图中,绘制了一条蓝色星形线作为最佳路径。同时,在左侧的3D地形图中,绘制了一条红线作为最佳路径。可以看出,所设计的路径规划算法可以有效地避免威胁,快速找到到达目标的最短路径,并紧贴3D安全飞行曲面之上飞行。

在图8(b)中单独绘制出了规划好最优轨迹(图8中红色曲线)和搜索过程中形成的最优航点的连线(图8中蓝色曲线),显然,最终的最优轨迹是在最优航点连线的基础上平滑处理之后得到的。

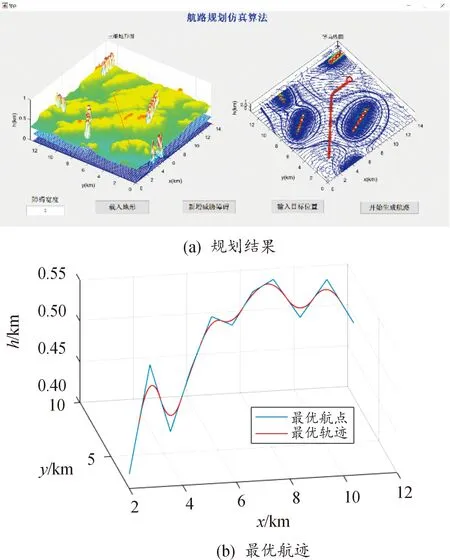
图8 三维最优路径规划结果

4 结论

本文中设计了一种无人机近地三维最优路径规划方法,通过仿真实验,可以得到以下结论:

1) 通过真实地图的数字高程模型作为无人机近地路径规划的地形数据来源是一种简洁、可行的地形建模方法。

2) 通过考虑安全高度、减小坡度和曲率等因素对原始数字地形进行预处理,可以有效的生成无人机的安全飞行曲面,形成对复杂三维地形的路径预规划。

3) 所设计的GUI程序可以加载优化后的安全飞行曲面,并通过最优算法避开威胁区域到达目标位置(其中威胁数量、威胁位置和目标位置可自由指定),获得最佳的飞行路径。

本文中设计的规划方法,在安全飞行曲面的基础上,可以避开特定的威胁,获得最佳的飞行路径,且满足无人机操纵性能的约束要求,为无人机近地三维路径规划的设计与仿真提供了一种新的思路。