考虑动态腐蚀的输流管道时变共振可靠性及灵敏度分析

郭 庆,翟红波,刘永寿

(1.西安近代化学研究所, 西安 710065;2.西北工业大学 力学与土木建筑学院, 西安 710129)

0 引言

输流管道广泛应用于航空、航天、航海、石油等装备之中[1-2],常受到宽频激励加载,内部液体与管道的流固耦合作用会使得管道的固有频率发生变化,流体介质的种类、流速和压力都会影响流固耦合作用的强弱,进而影响管道振动模态[3]。而服役于海洋、土壤深埋或严重酸雾环境的管道,易受到环境腐蚀,管道结构受到破坏,引起管道固有频率发生变化[4]。此外,在输流管道的设计、加工、装配和服役过程中,管道结构、内部流体和外部激励会不可避免的引入不确定性因素,而不确定性因素经由管道和流固耦合作用传递至管道固有频率响应,进而导致输流管道固有频率具有不确定性[5]。当管道固有频率与外部激励频率接近至一定程度时,会诱发管道共振现象,可能造成管道系统发生严重失效。

近年来,针对输流管道振动和可靠性问题,研究人员展开了大量研究。韩涛等[6]采用直曲组集方法对航空复杂液压管道的模态进行了分析,获得了管道布局对“Z”形管道固有频率的影响规律。翟红波等[7]针对均匀流和非均匀流输流管道,采用七点估计法分别求解了其共振可靠度。刘庆等[8]采用主动学习Kriging算法求解了变截面输流管道的一阶和二阶共振失效概率。Zhao等[9]将截断重要抽样法引入输流管道共振失效概率的求解,有效提高了计算效率。Zhang等[10]使用一阶可靠性方法分析了液压管道的时变失效概率。Rastogi 等[11]采用失效评估图法分析了带裂纹管道的可靠性水平。Liu等[12]提出了一种压力脉动和随机振动条件下液压管道可靠性定量分析方法。Carera-Miranda等[13]建立上拉细长管的控制方程和极限状态方程,分析了参数激励不确定性影响下的动态屈曲可靠性问题。Fan等[14]针对变直径功能梯度材料输流管道,采用基于自适应Kriging模型的算法求解输流管道多阶共振失效概率和灵敏度。目前,尚未有学者考虑管道遭受动态腐蚀对于共振失效的影响,亟需针对输流管道的时变共振可靠性问题开展研究。

由于时变可靠性问题通常为小失效概率问题,对于可靠性算法的计算效率要求较高。参考输流管道非时变共振可靠性研究经验,自适应代理模型算法求解非时变共振失效概率十分高效。因此,引入单层主动学习Kriging模型算法(SL-ALK)[15]与基于元模型的重要抽样法(Meta-IS)[16]结合的SL-ALK-Meta-IS算法[17]求解时变共振失效概率,并与MCS法、SL-ALK法对比验证其准确性和高效性。同时,为分析各输入随机变量对于管道时变共振可靠性的影响,建立变量全局灵敏度指标[18],求解得到的变量重要性排序可以为输流管道防共振优化设计提供参考。

本文中,采用Galerkin加权余量法求解输流管道固有频率,建立考虑动态腐蚀的输流管道时变防共振功能函数以及变量灵敏度指标,采用SL-ALK-Meta-IS法求解时变失效概率和变量重要性排序,分析管道结构密度、流体介质种类、流体流速对于时变失效概率的影响规律。

1 输流管道固有频率

考虑一长为Lp的两端简支等直输流管道,假定管内流体无粘且不可压缩,即管内流体均匀流速。根据小变形假设下的Euler-Bernoulli梁模型,输流管道的横向振动控制方程为

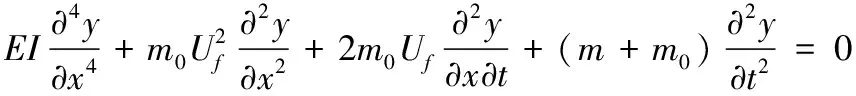
(1)

式(1)中:m0为单位长度管道内流体质量;m为单位长度管道质量;Uf为管道内的流体流速;EI为抗弯刚度;y为管道横向位移;x为管道轴向位移;t为时间。

引入变分法中的Galerkin加权余量法求解其近似解,假设,

y(x,t)=u(x)exp(iωt)

(2)

将y的函数代入方程(1),此时可以消去exp(iωt),即可得到

(3)

两端简支输流管道的边界条件为

(4)

方程(4)的试函数取为φλ(x)=sinβλx, (λ=1,2,…,N),此时的近似解函数为

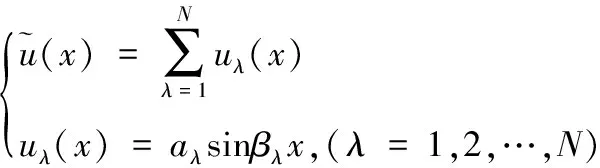
(5)

式(5)中:aλ为Galerkin系数;N为Galerkin截断阶数;βλ=λπ/Lp, (λ=1,2,…,N)。

将近似解(5)代入方程(3),可得余量

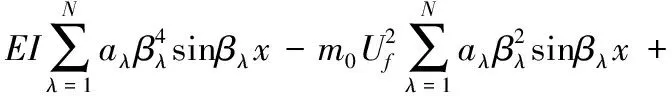
(6)

根据Galerkin法规定,权函数与试函数相等,即

Wλ(x)=φλ(x)=sinβλx,(λ=1,2,…,N)

(7)

为了消除余量R,作余量与权函数的内积,并令其正交,即

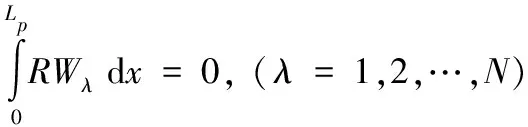
(8)

将方程(6)和(7)代入方程(8),可得

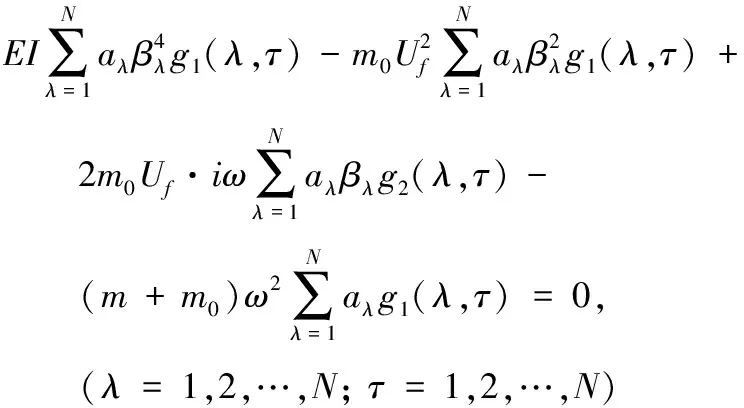
(9)

式(9)中:g1(λ,τ)和g2(λ,τ)分别为:

当λ=τ时,

(10)

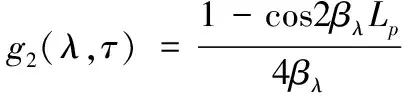
(11)

当λ≠τ时,

(12)

(13)

方程(9)即为Galerkin方程组,其矩阵形式为

(14)

(λ=1,2,…,N;τ=1,2,…,N)

式(14)中:C是Galerkin系数矩阵,是ω的函数。此外

2m0Uf·iωβλg2(λ,τ)-(m+m0)ω2g1(λ,τ)

(15)

方程(14)有非零解的充要条件为

det|C(ω)|=0

(16)

由方程(16)可以求出2N个ω,又因为方程(15)中含有虚数项,且复特征值共轭出现,再略去实部为负的特征值,可以得到N个ω,其实部即为固有频率。

2 时变防共振可靠性及灵敏度分析

2.1 时变防共振功能函数建立

g1(X,t)=(ω1(t)-S1)·(ω1(t)-S2)

(16)

式(16)中:X=(x1,x2,…,xndv)T;ndv表示输入变量的个数;ω1(t)表示与时间相关的一阶固有频率。

2.2 变量灵敏度指标

令(X,t)表示输入随机变量和时间参数的集合,tj(j=1,2,…,NT)为观察区间[t0,te]中的某个时刻,时变失效概率PF(t0,te)可表示为

PF(t0,te)=P{g(X,t)<0, ∃tj∈[t0,te]}

(17)

式(17)中:下标F表示失效域。

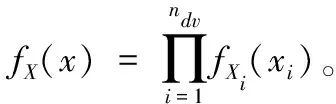
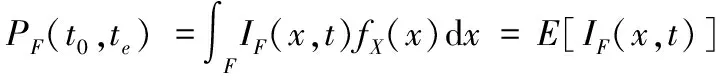
(18)

式(18)中:E[·]表示期望运算;IF(x,t)表示时变失效指示函数,具体表示为

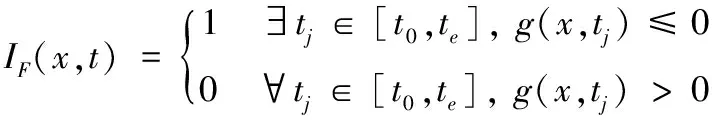
(19)

参考矩独立全局灵敏度指标的定义方法,将变量xi固定在其实现值时的条件时变失效概率PF|xi(t0,te)可以表示为

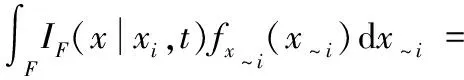
(20)

式(20)中:x～i表示除xi之外的输入变量;fx～i(x～i)表示x～i的概率密度函数。PF(t0,te)和PF|xi(t0,te)之间的差异反映了输入变量xi对时变失效概率的影响,将该差异A(xi)表示为平方形式即为

A(xi)=[PF(t0,te)-PF|xi(t0,te)]2

(21)

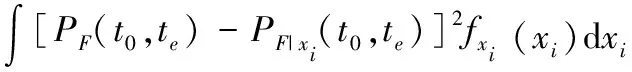
(22)

将式(18)和式(20)代入到式(22),可以得到

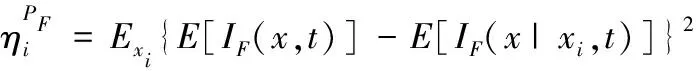
(23)

进一步参考广义灵敏度分析思想[18],将条件时变失效概率用贝叶斯公式表示为

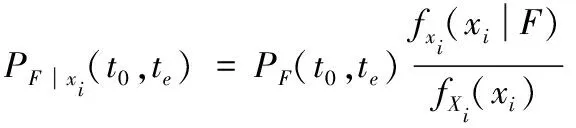
(24)

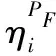
(25)

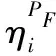
步骤1：根据每个输入变量的概率密度函数随机生成N个样本,并组成输入样本矩阵S。将时间区间[t0,te]均匀离散成NT个时刻组成时间向量T。

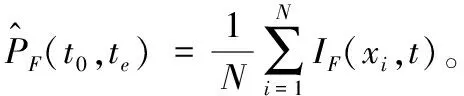
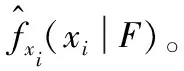
2.3 SL-ALK-Meta-IS算法

SL-ALK-Meta-IS法的计算流程总结如下:

步骤1：根据输入变量的概率密度函数fx(x)随机生成NX组样本,并组成样本集S={xi,i=1,2,…,Nx}。将时间区间均匀离散为NT个时刻组成时间向量T={tj,j=1,2,…,NT}。

步骤2：从S和T中随机选择NINI个样本组成初始训练样本集SINI={(xk,tk),k=1,2,…,NINI}。将初始训练样本代入时变功能函数g(xk,tk)计算对应的输出响应,并组成训练集ST={(xk,tk),g(xk,tk),k=1,2,…,NR}。此时功能函数调用次数为NR=NINI。

步骤3：根据训练集ST建立Kriging模型gK(x,t)。

步骤4：基于建立的gK(x,t),根据式(26)估计概率分类函数π(x,t),进而根据式(27)建立重要抽样密度函数hx(x)。根据hx(x)生成NIS个重要抽样样本SIS={xi,i=1,2,…,NIS}。SIS即为此时的候选样本池SC。

(26)

(27)

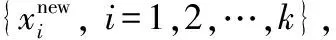
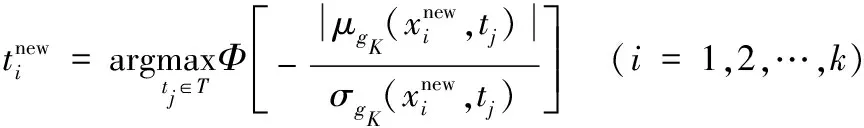
(28)

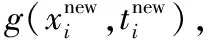
(29)

步骤8：基于S估计增广失效概率PFε,对应的方差和变异系数

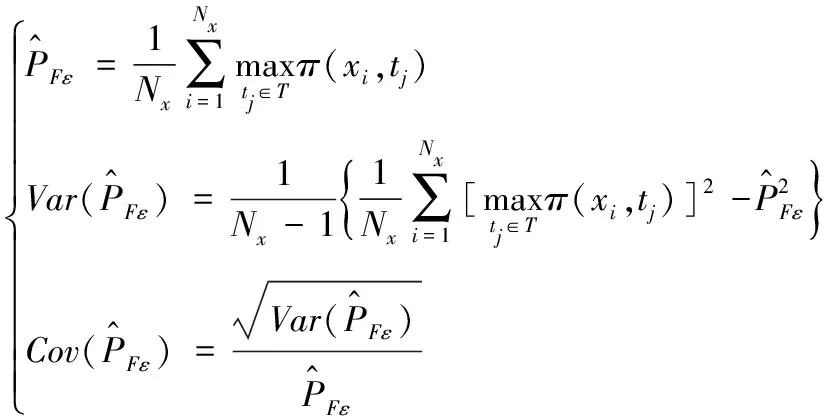
(30)

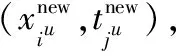
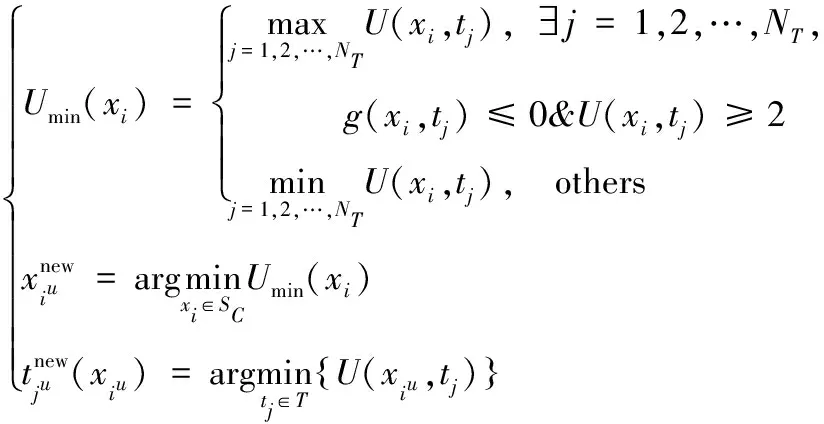
(31)

步骤10：根据训练集ST更新Kriging模型。

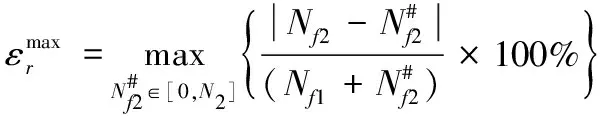
(32)

步骤12：估计修正因子,对应的方差和变异系数

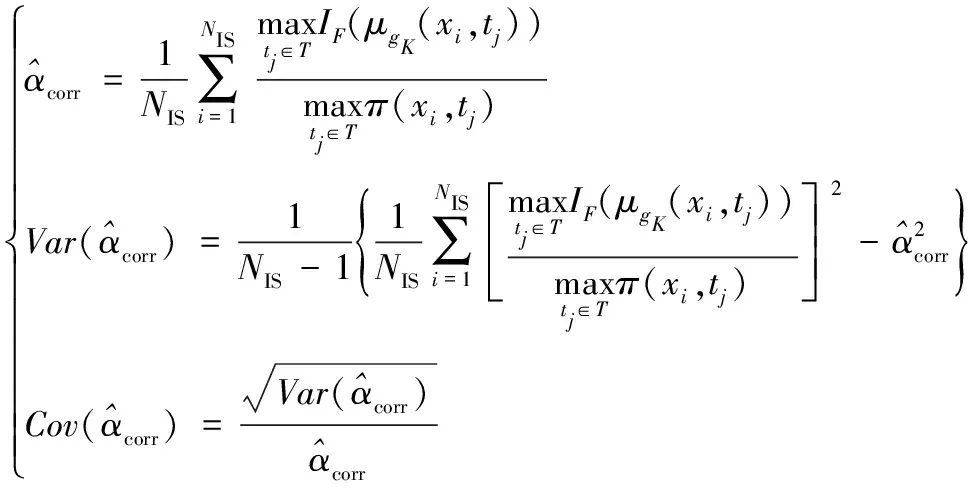
(33)

步骤13：估计时变失效概率和对应的变异系数

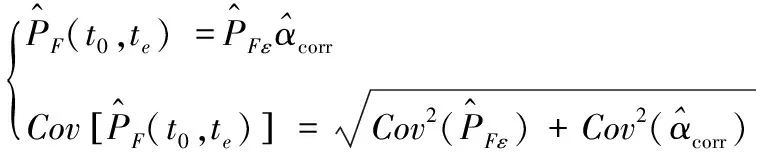
(34)

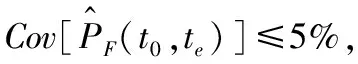
关于SL-ALK-Meta-IS算法的技术细节参见文献[17]。

3 算例分析

本节参考文献[19]中的两端简支输流管道模型作为算例。管道结构示意图如图1所示,管道长度为Lp=2 m,初始外直径d0=0.1 m,初始壁厚h0=0.002 m,管道材料弹性模量E=68.6 GPa,密度ρ=2 800 kg/m3,泊松比0.3,管内流体密度ρf和流速Uf分别考虑4种工况。考虑的随机变量信息如表1所示。时间观察区间为t∈[0,15]年,管壁腐蚀速率为κ=0.05 (mm/年)。采用MCS法、SL-ALK法和SL-ALK-Meta-IS法来计算时变共振失效概率,ALK法的初始训练点数量为12,SL-ALK法候选样本点数量为105,SL-ALK-Meta-IS法的候选样本点数量为3 000。

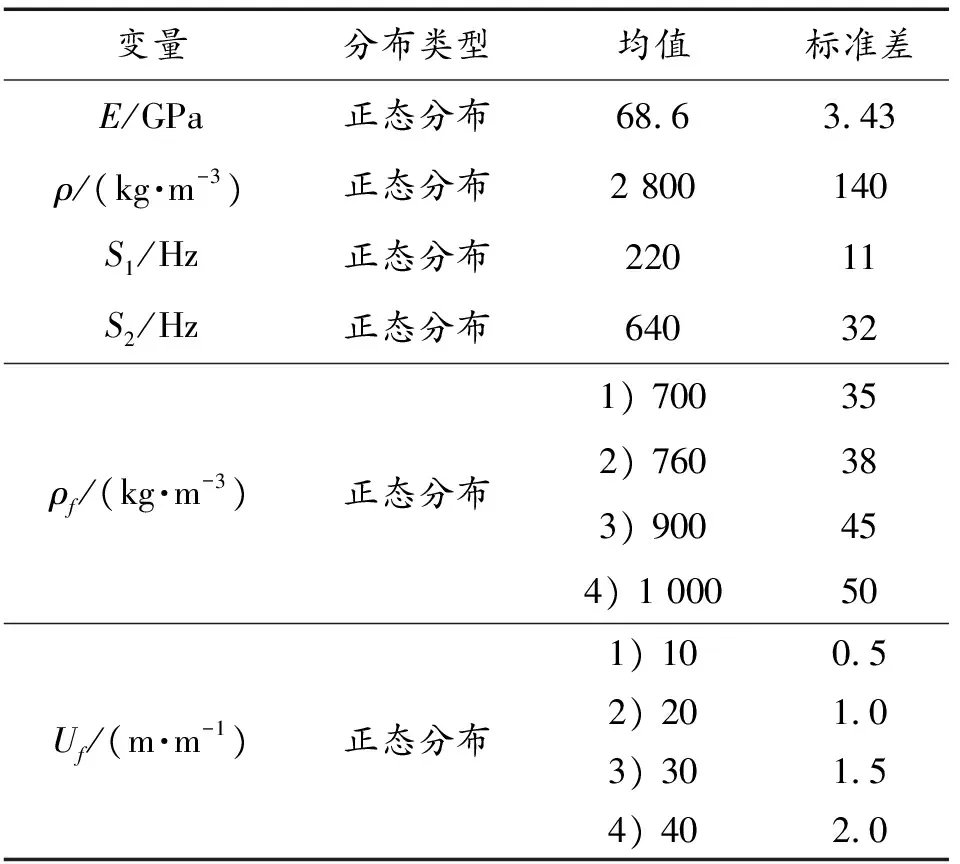
表1 输入变量的随机分布类型及参数

图1 两端简支输流管道示意图

3.1 方法验证

首先验证SL-ALK-Meta-IS法计算输流管道时变共振失效概率的准确性。考虑流体密度工况为ρf=1 000 kg/m3,流速工况为Uf=40 m/s。MCS法、SL-ALK法和SL-ALK-Meta-IS法计算得到的输流管道时变共振可靠性和灵敏度分析结果如表2所示。与MCS法和SL-ALK法的结果相比,SL-ALK-Meta-IS法计算得到的时变共振失效概率误差很小,鲁棒性较高。计算效率方面,SL-ALK-Meta-IS法利用Meta-IS法生成候选样本池时调用了34次功能函数,自适应加点时仅调用了107.2次功能函数,少于MCS法和SL-ALK法功能函数调用次数。此外,Kriging模型迭代速度方面,相同计算条件(Intel(R) Core(TM) i7-6700 CPU @ 3.40 GHz)下,SL-ALK-Meta-IS法每新增一个训练样本点仅需要6.19 s,明显少于SL-ALK法的47.80 s,这得益于SL-ALK-Meta-IS法的候选样本池规模较小。功能函数调用次数和Kriging模型迭代速度均证明了采用SL-ALK-Meta-IS法处理输流管道时变共振失效概率问题时具有极高的计算效率。

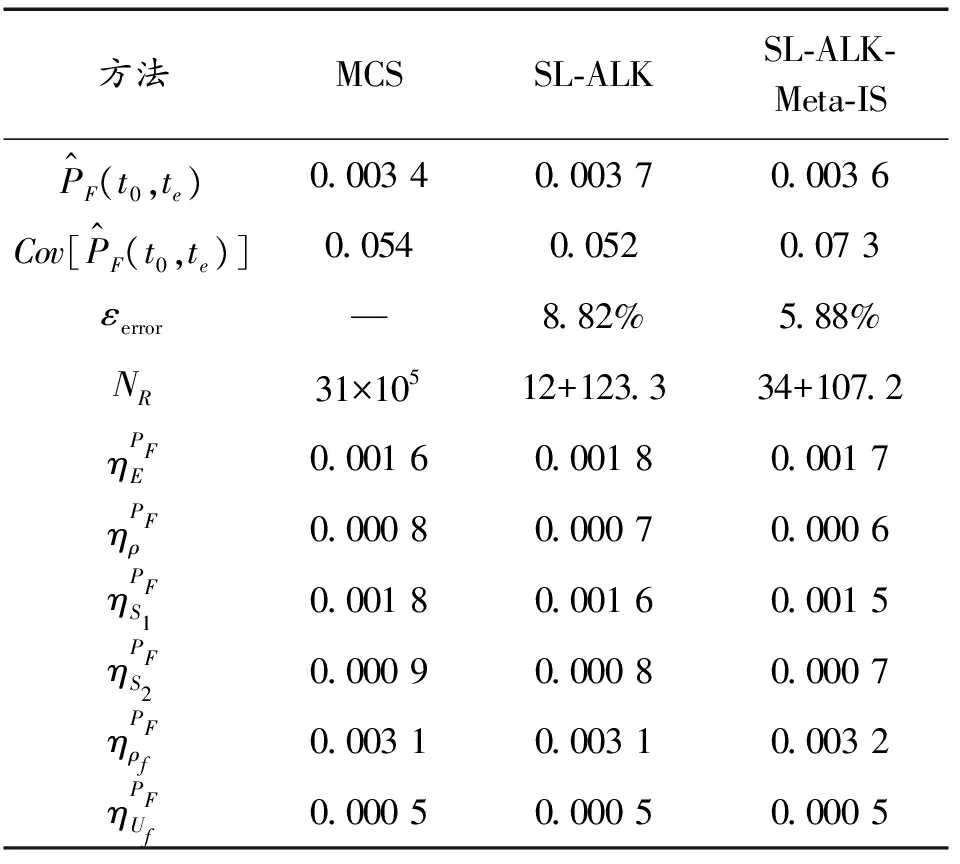
表2 输流管道时变共振可靠性及灵敏度分析结果

灵敏度分析结果如图2所示,3种方法估计得到的输入变量灵敏度指标值基本一致,各变量重要性排序相同,均为ρf>E≈S1>ρ≈S2≈Uf,说明输入变量ρf的不确定性对于时变共振失效概率的影响最大,接下来是E和S1,其余3个变量的不确定性贡献度明显较低。时变共振失效概率随变量变异系数增长的变化如图3所示,其中某一变量的变异系数由0.03增长到0.065时,其他变量分布保持不变。可以发现,输入变量增长等量的不确定性,输入变量ρf会导致时变共振失效概率增长幅度最大,随后依次是E和S1。其余变量变异系数的增长几乎不会改变时变共振失效概率。图3中的结果充分证明了灵敏度分析结果的有效性。

图2 输入变量灵敏度结果柱状图

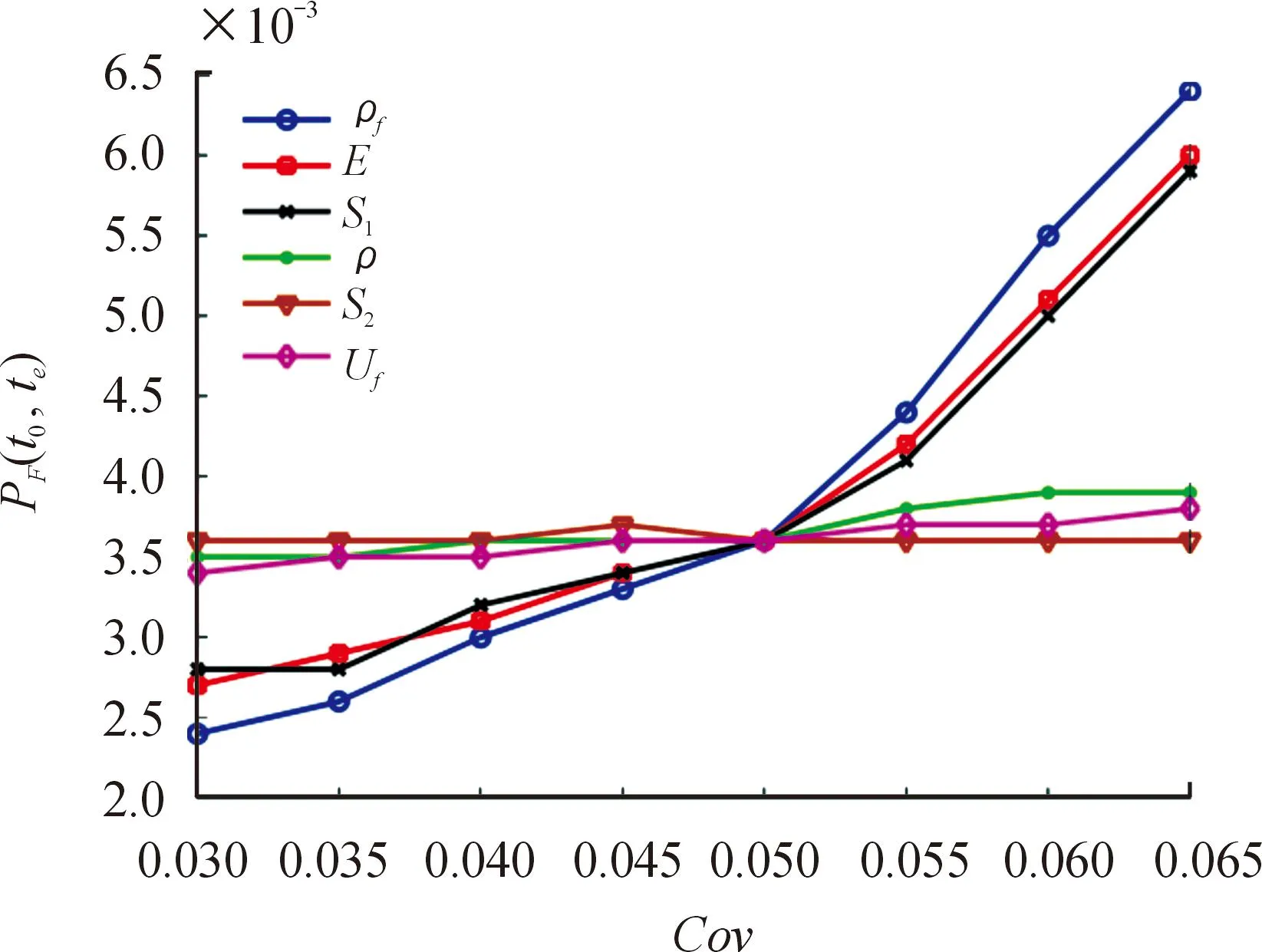
图3 时变共振失效概率随变量变异系数 增大的变化曲线

此外,基于广义灵敏度分析思想的时变可靠性全局灵敏度指标求解效率极高,仅需要一组样本即可同时完成时变共振失效概率和灵敏度的求解,无需额外调用功能函数计算,证明了本文中建立的输流管道时变共振可靠性和灵敏度求解策略的准确性和高效性。

3.2 流体密度对时变共振失效概率的影响

考虑4种流体密度均值工况:①ρf=700 kg/m3;②ρf=760 kg/m3;③ρf=900 kg/m3;④ρf=1 000 kg/m3。以上均为输流管道典型输送介质,工况1为汽油密度,工况2为石油密度,工况3为煤油密度,工况4为水密度。设此时流速工况为Uf=40 m/s。各方法计算得到的各工况的失效概率结果如表3所示。可以看到,SL-ALK-Meta-IS法估计的时变共振失效概率结果与MCS法和SL-ALK法基本一致,而随着流体介质密度的增大,时变共振失效概率急剧下降,说明管道输送介质的改变对于输流管道的可靠性与安全性影响明显,利用管道输送不同介质时开展对应的时变共振可靠性分析是十分必要的。

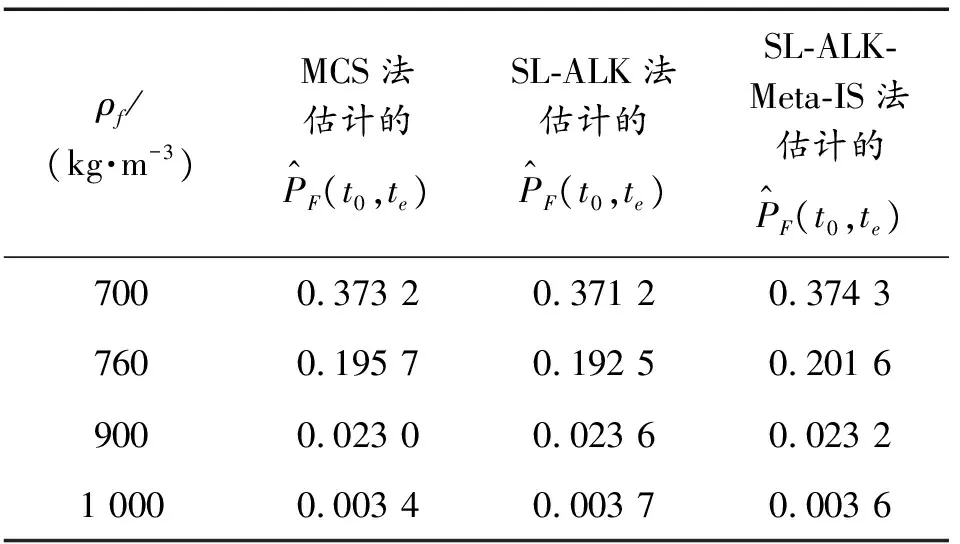
表3 不同流体密度工况下输流管道时 变共振失效概率结果

3.3 流体流速对时变共振失效概率的影响

考虑4种流速均值工况:①Uf=10 m/s;②Uf=20 m/s;③Uf=30 m/s;④Uf=40 m/s。设此时流体密度工况为ρf=1 000 kg/m3。各方法计算得到的不同工况下的时变共振失效概率如表4所示。结果表明,随着流速的增大,输流管道时变共振失效概率逐渐降低,这与文献[19]中所考虑的时不变共振失效概率随流速增大的变化规律相同,这主要由于管道固有频率随流速增大而逐渐减小,从而逐渐远离外激励频率所致。

表4 不同流体流速工况下输流管道时 变共振失效概率结果

4 结论

建立了考虑动态腐蚀的时变共振功能函数,通过算例分析验证了所提输流管道时变共振可靠性及灵敏度分析策略的有效性和高效性,并且讨论了管道流体介质和流速等因素对于时变共振失效概率的影响规律。结果证明:

1) SL-ALK-Meta-IS法可以准确、高效地求解输流管道时变共振失效概率和输入变量灵敏度值。

2) 随着流体密度的增大,管道时变共振失效概率会急剧下降,而随着流速的增大,管道时变共振失效概率会逐渐减小。

3) 基于SL-ALK-Meta-IS法的输流管道时变共振可靠性及灵敏度分析方法对于输流管道可靠性和安全性评估以及防共振优化设计具有重要参考价值和指导意义。