天然气计量中物性计算方法适用性探讨

连子超 杨妮 李学成 许佳 代晓雨 吴萍

（1.华北油田公司华港燃气集团；2.中国石油西南油气田公司华油公司重庆凯源石油天然气有限责任公司；3.国家石油天然气管网集团北方管道大庆输油气分公司；4.国家管网集团山东省分公司德州作业区；5.中国石油吐哈油田分公司工程技术研究院地面工程设计所）

在天然气体积计量中，密度、压缩因子、发热量等参数是确定管道流量的重要参数[1-2]。常规可通过实验仪器在线或离线测量，但这无疑增加了工程应用的成本[3]。状态方程法在计算天然气物性上的应用范围最广、计算精度最高，1992 年美国燃气协会（AGA）发布了用于计算天然气物性值的AGA8号文件（第一版）[4]，其中的AGA8-92DC 状态方程在天然气贸易交接和输差分析领域上发挥了积极作用，国内GB/T 17747.2—2011《天然气压缩因子的计算 第2 部分： 用摩尔组成进行计算》 和GB/T 30491.1—2014《天然气热力学性质计算第1部分：输配气中的气相性质》均基于AGA8-92DC状态方程计算天然气物性。2017 年AGA 发布了AGA8 号文件（第三版），并在第二部分介绍了GERG-2008 状态方程的方法[5-6]，同等标准为国际标准化组织（ISO） 发布的ISO 20765-2： 2015《Natural gas-Calculation of thermodynamic properties-Part2:Single-phase properties (gas，liquid，and dense fluid)for extended ranges of application》，该方程组分关系参数的回归是在3 万个天然气随机组分的基础上得到的，因此在混合复杂气体物性和相平衡的计算上具有优越性。目前，关于两种方法在不同组成、不同相态天然气物性上的计算结果差异还鲜有报道，这对于现场中选用何种方法进行天然气计量息息相关。基于此，在GB/T 17747.2—2011 和ISO 20765-2：2015 的基础上，收集文献中的实验数据，对比AGA8-92DC 和GERG-2008 两种状态方程在计算天然气物性上的差异性和适用范围，以期为天然气的准确计量提供实际参考。

1 算法原理及程序有效性验证

1.1 AGA8-92DC 状态方程

该算法的核心方程是一种二维外延式的Virial方程[7]，公式见式（1）：

式中：Z为压缩因子；B为第二Virial 系数，为中间过程变量；ρm为摩尔密度，kmol/m3；ρr为对比密度，无量纲；为与气体组分和温度相关的系数，为中间过程变量；bn、cn、kn为状态方程常数参量。

AGA8-92DC 状态方程的求解步骤是先输入温度、压力和气体摩尔组分，计算方程中的B和；随后联立状态方程与压缩因子的定义式，得到关于ρm的一元超越方程；随后将ρm视为自变量，赋予一定的初值，代入状态方程求解，得到压力p的计算值；最后，将计算值与真实压力值对比，当两者之间的差值绝对值在规定范围内（10-6），则确认此时的ρm为所需摩尔密度，进而求解得到压缩因子及一系列物性参数，否则，重新预设ρm初值，进行重复求解，直到收敛为止。

1.2 GERG-2008 状态方程

该方程的基础是Helmholtz 自由能方程，通过混合气体中不同组分基本状态方程和衍生物的关系确定流体物性，并通过大量实验数据拟合到传统立方型方程得到回归系数[8]。GERG-2008 状态方程可以表示为两部分，一是理想气体的Helmholtz 能量α0，二是实际气体的Helmholtz 能量αr，其无量纲形式为：

式中：α为Helmholtz 能量，无量纲；d为介质密度，kg/m3；T为热力学温度，K；x为摩尔组分；为第i个组分的理想Helmholtz 能量，无量纲；为第i个组分的Helmholt 自由能余相，无量纲；xi、xj分别为第i个、第j个组分的摩尔分数；Fij为二元调节因子；为偏差函数；δ为对比密度，无量纲；τ为对比温度的倒数。

GERG-2008 状态方程的求解步骤是先输入混合物的温度、压力和摩尔组分，随后设置初始介质密度d，计算δ和τ；随后计算混合物Helmholtz 自由能余相关于对比密度的偏导数，进而确定混合物压力；将计算压力与实测压力对比，当两者之间的差值绝对值在规定范围内（10-6），则输出d作为真实介质密度，并计算天然气压缩因子及一系列物性参数；否则，重新预设d初值，进行重复求解，直到收敛为止。

1.3 有效性验证

在GB/T 17747.2—2011 和ISO 20765-2：2015的基础上，采用Matlab 软件建立AGA8-92DC 和GERG-2008 状态方程天然气物性求解程序，并利用附录中的计算示例进行程序验证，计算示例范围见表1。不同状态方程的计算结果对比见图1，可见以两种状态方程为基础的程序计算结果与附录中的压缩因子值基本吻合，相对误差在±0.1%以内，证明了编制程序的有效性和可靠性，可以作为后续研究的基础。

图1 不同状态方程的计算结果对比Fig.1 Comparison of calculation results of different equations of state

表1 计算示例范围Tab.1 Calculates sample ranges

2 天然气物性计算值与实验值对比

收集文献中真实气体的实验值（实验方法为磁悬浮测试法或Burnett 装置法），将AGA8-92DC 和GERG-2008 状态方程的计算结果与其对比，以此评估计算方法的准确度差异。以相对偏差（RD）和平均相对偏差（ARD）为评价指标，见下式：

式中：CRD为相对偏差；CARD为平均相对偏差；Zcal为压缩因子计算值；Zexp为压缩因子实验值；Zcal,i为第i个数据的压缩因子计算值；Zexp,i为第i个数据的压缩因子实验值。

2.1 压缩因子

2.1.1 管输天然气

GB/T 17747.2—2011 和ISO 20765-2：2015 分别规定了两种状态方程的计算适用范围，在规定的范围内选取5 组天然气数据进行计算，共获取513 个压缩因子数据，5 组管输天然气组分见表2。

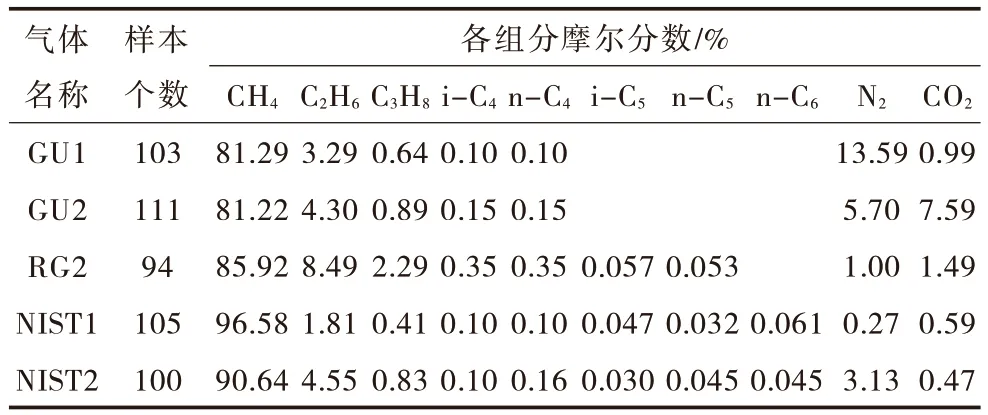
表2 5 组管输天然气组分Tab.2 Five groups of pipeline natural gas composition

在常规天然气管输压力0～10 MPa、温度280～320 K 的范围内，两种状态方程计算得到的压缩因子结果准确度一致，压缩因子的ARD 为0.03%；在高压大于10 MPa、温度280～350 K 的范围内，两种方法的计算结果准确度差异不大，GERG-2008状态方程的准确度略高；在温度250～280 K 的范围内，两种方法的计算结果准确度存在较大差异，GERG-2008 状态方程的结果明显优于AGA8-92DC状态方程，这是由于该温度范围接近露点线或泡点线，在气液两相界面处AGA8-92DC 状态方程的适用性有所降低，GERG-2008 状态方程对于中间质量天然气的管输压力和温度适用范围分别是0～70 MPa、60～700 K，因此GERG-2008 状态方程的适用范围更广。此外，高压、低温环境下的压缩因子准确度较差，在同一压力范围内，随着温度的升高，ARD 的分布范围逐渐变小。管输天然气压缩因子ARD 的计算结果见表3。

表3 管输天然气压缩因子ARD 计算结果分布情况Tab.3 Distribution situation of ARD calculation results for pipeline natural gas compression factor

2.1.2 高含硫天然气

目前，我国在四川、塔里木、准格尔和渤海湾等地均发现了大型高含硫气田，气质组分中H2S 的含量较高。在张砚，熊治富等[8-9]研究和对天然气偏差系数计算方法中收集8 组高含硫天然气数据进行计算，共获取268 个压缩因子数据，8 组高含硫天然气组分见表4。

表4 8 组高含硫天然气组分Tab.4 Eight groups of high sulfur gas fractions

按照H2S 含量的高低计算不同组分和工况下的ARD 值。 横坐标以H2S 含量从低到高排，AGA8-92DC 状态方程的ARD 值先增大后减小，在H2S 含量大于50%时，公开文献数据已无法计算压缩因子；GERG-2008 状态方程的ARD 值在H2S含量为5.7%～22.6%，呈先增大后减小趋势；H2S含量为50.64%～91.67% ， 同样地呈先增大后减小趋势。 按照GB/T 26979—2011《天然气藏分类》中对含H2S 气藏的分类标准，AGA8-92DC 方程和GERG-2008 方程均在高含硫气藏压缩因子的计算上存在较大偏差。 对于M3、 M4 气体，AGA8-92DC 状态方程的计算表现较优；对于M1、M2、M5 气体，GERG-2008 状态方程的计算表现较优； 综合分析， AGA8-92DC 状态方程和GERG-2008 状态方程的ARD 值分别为0.86%、0.95%，说明AGA8-92DC 状态方程的计算效果更好。高含硫天然气的ARD 计算结果见图2。

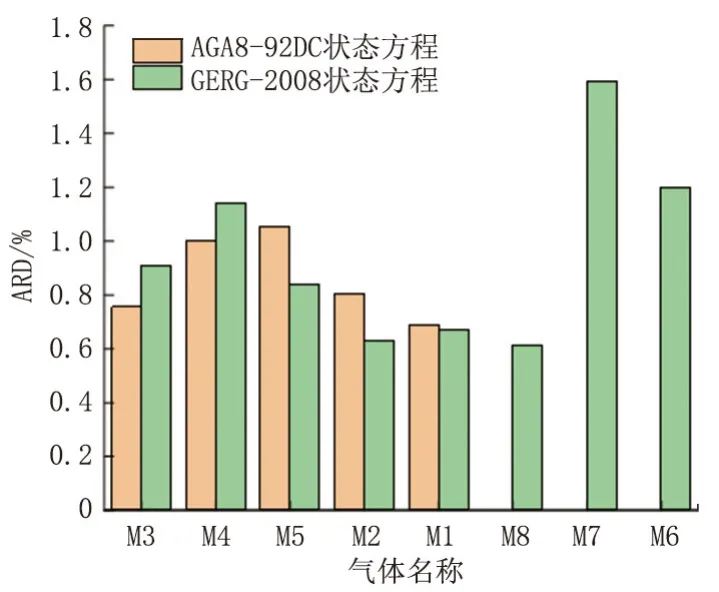
图2 高含硫天然气的ARD 计算结果Fig.2 ARD calculation results of high sulfur gas

2.2 密度

2.2.1 含重烃天然气

收集6 组含重烃天然气数据进行计算，共获取170 个密度数据，6 组含重烃天然气组分见表5。

表5 6 组含重烃天然气组分Tab.5 Six groups of heavy hydrocarbon containing natural gas

含重烃天然气密度ARD 的计算结果见表6。在常规天然气管输压力0～10 MPa、温度280～320 K 的范围内，两种状态方程计算得到的压缩因子结果准确度基本一致，GERG-2008 状态方程的准确度略高；在压力小于30 MPa，温度为250～500 K，GERG-2008方程的计算表现更优；在压力大于30 MPa，部分温度范围内AGA8-92DC 状态方程的计算表现优于GERG-2008 状态方程。此外，虽然天然气物性种类有所不同，但从ARD 分析，表6 的ARD 无论是分布范围还是波动幅度均大于表3 中的ABD，含重烃天然气中C4、C5的含量明显大于管输天然气，说明重烃可增大状态方程计算结果的误差。

表6 含重烃天然气密度ARD 计算结果分布Tab.6 Distribution of ARD calculation results of natural gas density containing heavy hydrocarbons

以表5 中的Patil 气体为例，计算不同温度、压力下的密度值。AGA8-92DC 状态方程的计算结果多大于实验值，GERG-2008 状态方程的计算结果多小于实验值，说明GERG-2008 状态方程获得的天然气实际体积流量较小，这在下游天然气贸易交接中买方会占有较大优势。通过对Patil 气体进行物性分析，得到其临界凝析温度为237.5 K，可见气体温度越接近临界凝析温度，密度计算结果的准确度越低，且AGA8-92DC 状态方程的最大RD 达到0.64%，GERG-2008 状态方程的最大RD 为-0.44%，再次证明了GERG-2008 状态方程计算结果的准确性。Patil 气体密度计算结果对比见图3。

图3 Patil 气体密度计算结果对比Fig.3 Comparison of calculation results for Patil gas density

2.2.2 液化天然气

收集4 组液化天然气数据进行计算[10]，共获取210 个密度数据，4 组液化天然气组分见表7。

表7 4 组液化天然气组分Tab.7 Four groups of liquefied natural gas composition

计算不同组分和工况下的ARD 值。 GB/T 17747.2—2011 中规定AGA8-92DC 状态方程的适用范围为天然气、含人工掺合物的天然气和其他类似混合物，但要求介质均为气态存在；ISO 20765-2：2015 中的计算范围包括均质（单相）气体状态、均质液体状态或均质超临界（致密流体）状态条件下的天然气。从规范范围上分析，AGA8-92DC 状态方程的计算范围已无法涵盖液化天然气的运行工况， 该方程的计算结果偏差较大； 采用GERG-2008 状态方程的计算结果更优，除LNG3、LNG4 两个重烃含量较高的气体存在较大误差，其余气体的ARD 值在0.2%以内，考虑到国际LNG 船运交接时对丁烷和戊烷含量有要求， 故GERG-2008 状态方程可用于液化天然气的物性计算。液化天然气的ARD 计算结果见图4。

图4 液化天然气的ARD 计算结果Fig.4 ARD calculation results of liquefied natural gas

3 结论

1） 在常规天然气管输压力和温度的范围内，AGA8-92DC 状态方程和GERG-2008 状态方程计算得到的压缩因子结果准确度一致，ARD 为0.03%；高压、低温环境下的压缩因子准确度较差，随着温度的升高，ARD 的分布范围逐渐变小。

2） 对于含重烃天然气， 在压力较低时GERG-2008 状态方程的计算效果更好；与常规天然气相比，重烃的存在会增大计算结果的误差。

3）AGA8-92DC 状态方程可用于计算高含硫天然气压缩因子的计算；当国际贸易交接对重烃含量有要求时，可使用GERG-2008 状态方程计算液化天然气的密度。