永磁同步直线电机全速域无传感器控制
周舒鹏
(安徽理工大学,安徽淮南,232001)
0 引言
永磁同步直线电机(Permanent magnet synchronous linear motor,PMSLM)因具有远行程、大推力、高精度等优点而被广泛应用于工业领域中。目前,在PMSLM 驱动控制系统中,通过机械传感器实时检测PMSLM 的位置与速度信号,而传统机械位置传感器价格昂贵、安装困难、精度易受环境影响。因此,无位置传感器的控制研究方法应时而生。目前,主要的无位置传感器控制方法有以下几类:基于模型参考自适应的估计方法、基于滑模观测器的估计方法、基于拓展卡尔曼滤波的估计方法、基于高频信号注入的估计方法[1]。前三类方法在高速运行时可较好地估算PMSLM 的速度和位置情况,PMSLM 静止与低速运行时,因反电势信号微弱,因而估算效果较差。第四类方法通过外加高频信号,检测电机起动和低速运行时的速度和位置,电机高速运行时会引起推力波动,产生附加损耗,因而高频注入法常用在低速运行时段。
为减小低速向高速切换的速度误差,更好预估PMSLM运行位置,本文采用两种不同的估计算法。在PMSLM 起动与低速运行阶段,采用高频信号注入法;在高速运行阶段,选用基于超螺旋滑模观测器的观测方法;PMSLM 由低速向高速运行过渡区间,利用两种估计算法结果的加权平均值的复合滞环算法,最后通过仿真验证算法的可行性。
1 脉振高频电压信号注入法
当电机起动或低速时,反电动势幅值很小,无法使用基于反电动势的控制方法。因此,本文提出使用脉振高频信号注入法(High frequency signal injection method,HFI),注入高频电压信号,通过检测携带动子位置和速度信息的高频电流响应,进而提取出电机相应的电机位置与速度信息[2]。
忽略PMSLM 的涡流损耗和端部效应的影响,则PMSLM在同步旋转d-q坐标系下的模型为:
式中:ud、uq分别为d-q轴的电压;R为定子电阻;id、iq分别为d、q轴的电流;ψd、ψq分别为d-q轴的磁链;Ld、Lq分别为d、q轴电感;ωe为电角频率;p为微分算子。
在PMSLM 的估计轴轴注入幅值为Vh,频率为ωh的高频余弦电压信号,注入的信号满足下式:
式中:udˆh、uqˆh为估计轴-的高频电压。
由于该方法主要用于零速和低速段,电机实际的旋转角频率ωe很小,式(1)中反电动势ωeψf可忽略不计。因为电机旋转角频率ωe远低于注入的高频电压信号频率ωh,此时电机的绕组阻抗主要是自感的感抗,电枢电阻R≈ 0,式(1)可简化成纯电感模型。
式中:udh、uqh分别为d-q轴高频电压信号注入后的电压;idh、iqh分别为高频电压信号注入后的电流响应;Ldh、Lqh分别为高频信号注入后的电感。
经高频电压注入后,估计轴系-的电流转换为旋转轴系d-q的电流:
式中:idˆh、iqˆh为估计轴系-的电流。
结合式(2)(3)(4)可得:
分析式(5)可知,若位置误差θ˜=0,则只有dˆ 轴的电流分量idˆh存在动子位置误差。因此,若要获得高频信号idˆh,需要添加带通滤波器(BPF)来滤除频率远大于注入频率的载波频率信号和远低于注入频率的基波频率信号,然后将滤波后的idˆh与调制信号sinωht相乘,最后通过低通滤波器滤波后得到调节器所需的输入量f(Δθ)[3],则:
将所得的电角度误差送入PI 调节器中使得=0,可得θe=,即高频电压信号注入后,电机估计位置跟随实际的位置。通过PMSLM 的机械运动方程可提取出动子的运动速度和位置信息。
式中:M为电机质量,v为电机运行速度,Fe为电磁推力,Fl负载阻力,B为粘滞系数。
2 超螺旋滑模观测器法
高频信号注入法在电机零速和低速时能准确判断电机的位置和速度,但该方法适用于电机低速运行阶段,高速运行时,高频信号在交轴产生的高频损耗与转矩波动较大。因此,在电机中高速运行时,需采用其他方法来预估电机的位置与速度情况。目前,滑模观测器法常用的是传统一阶滑模观测器(Sliding Mode Observer,SMO)。由于电机反电动势包含电机的速度与位置信息,因此,SMO 法以给定电流与反馈电流的误差为基础,根据该误差对电机反电动势进行重构,最后利用电机反电动势来推算出电机的位置与速度信息。SMO 调试方便,结构简单,但易产生抖振、位置跟踪误差大、鲁棒性弱的情况,虽可利用滤波器法降低抖振,但会导致相位延迟。本文采用的是超螺旋滑模观测器方法(Super-Twisting SMO,STSMO),超螺旋滑模观测器法是在SMO 基础上提出的,STSMO 是在连续的积分环节中进行符号函数切换[4],此方法削弱了电机抖振,缩短了调整时间,使得位置与速度估计结果更为精确。
在电机两相静止α-β轴中,永磁同步直线电机的电流方程为:
式中:iα、iβ分别为α-β轴的电流;L为电枢电感;uα、uβ分别为α-β轴的电压;Vα、Vβ为电机的反电动势。
在α-β坐标系中构建滑模观测器模型中,Supertwisting 的算法形式:
式中:x1、x2为系统的状态变量;k1、k2为滑模增益;ε1、ε2为扰动变量。
基于超螺旋滑模算法的PMSLM 数学模型构建的观测器为:
式(10)和(11)中:、分别为α-β轴滑模估算电流。
由式(10)、式(11)分别减去式(8)可得到电流误差方程为:
此时滑模观测器的控制输入Vα和Vβ分别等效于电机的反电动势Eα与Eβ:
由于等效反电势Eα、Eβ具有非连续性的特点,波形存在一定程度的失真,因而不能直接用来估算动子的位置和转速。为此,需要在滑模观测器的输出侧需加一个截止频率为wc的低通滤波器,低通滤波器滤除高次谐波后,获得与实际反电势等效且连续的滑模控制器的观测反电动势、。
将观测反电动势、引入锁相环的结构内,通过锁相环可估算出电机的速度与位置信息,锁相环结构框图如图1 所示。
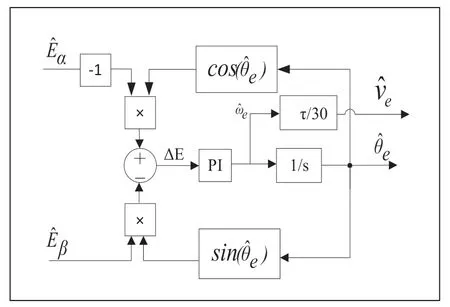
图1 锁相环结构框图
图1 中,τ为PMSLM 的极距。经过锁相环的相关运算后,观测反电动势误差ΔE可表示为:
将观测反电动势误差ΔE引入PI 调节器中,可得出电机动子的估计角速度,经过积分环节得出动子的预估位置。由直线电机的速度公式=()/30可计算出永磁同步直线电机的估计直线运动速度。
3 HFI 和STSMO复合估计法
为了准确估计永磁同步直线电机从低速到中高速的位置和速度情况,需要采用适当的切换机制来实现电机速度的平滑切换。目前,切换机制可分为单点切换法与复合滞环切换法两类。单点切换法通过设定一个阈值,在切换点的左右区间实行不同估计算法的切换。为了提高切换精度,避免发生抖振,本文采用加权系数法来实现滞环区间的过渡阶段的平稳衔接,使得两种估计算法能够平滑切换。滞环切换区间内的加权算法可设计为:
4 仿真研究
在Matlab/Simulink 仿真环境中搭建基于上述算法的PMSLM 无位置传感器控制系统,结构框图如图2 所示。
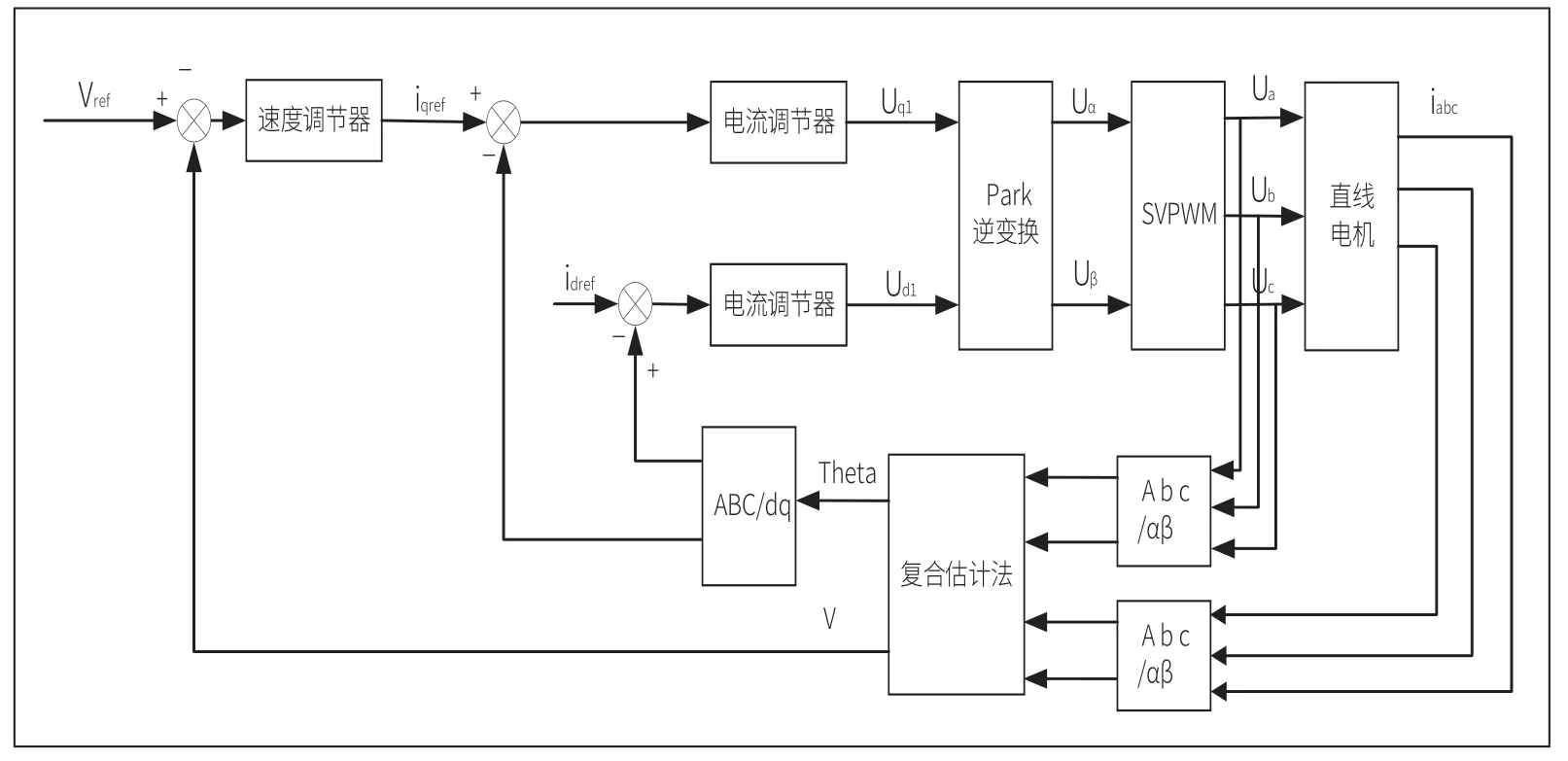
图2 无位置传感器控制系统图
所用的PMSLM 的参数如表1 所示。
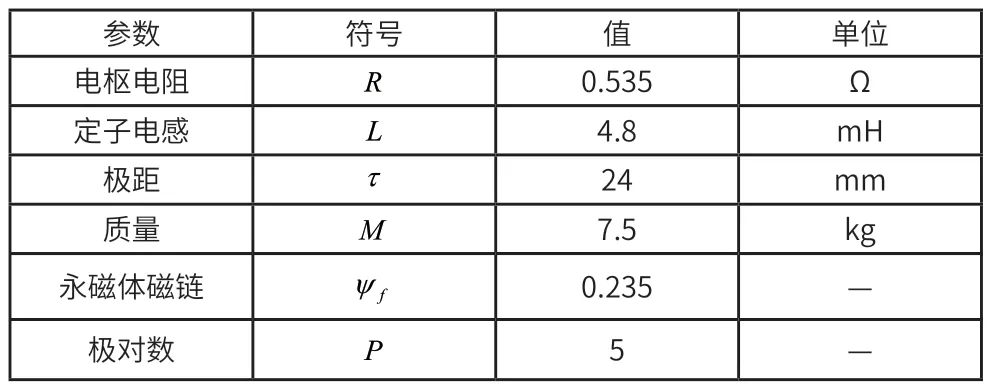
表1 永磁同步直线电机参数
根据仿真中的PMSLM 的全速域所适应区间,可确定切换区间为[0.1m/s,0.7m/s]。初始给定期望速度为1m/s,空载运行至0.4s。0.4s 时突加100N 的负载,0.75s 时给定期望速度为1.2m/s。
传统机械传感器的仿真结果、STSMO-HFI 无位置传感器控制方法的仿真结果如图3~8 所示。图3 为传统机械传感器速度输出值,图4 为传统机械传感器的电机速度误差图,图5 和图6 分别为STSMO-HFI 速度和位置输出值,图7 和图8 分别为STSMO-HFI 速度、位置实际值和估计值的差值。

图3 传统机械传感器电机速度
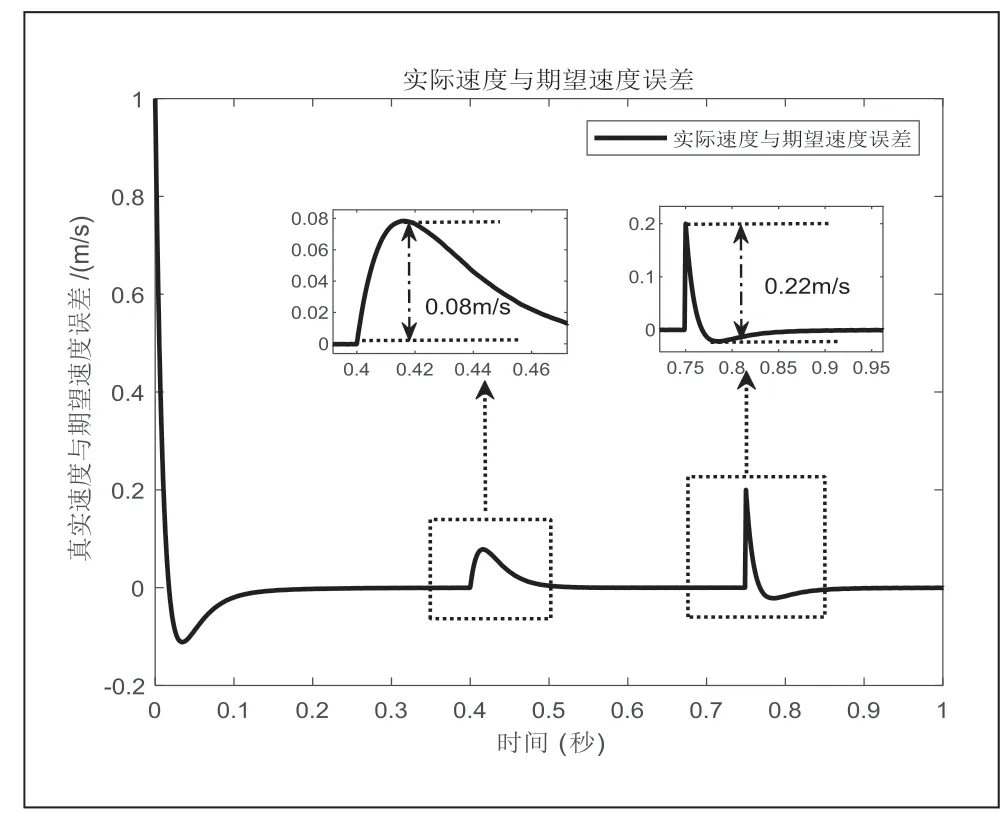
图4 传统机械传感器电机速度误差
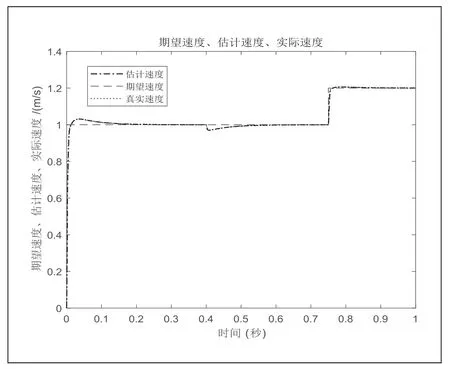
图5 STSMO-HF 速度
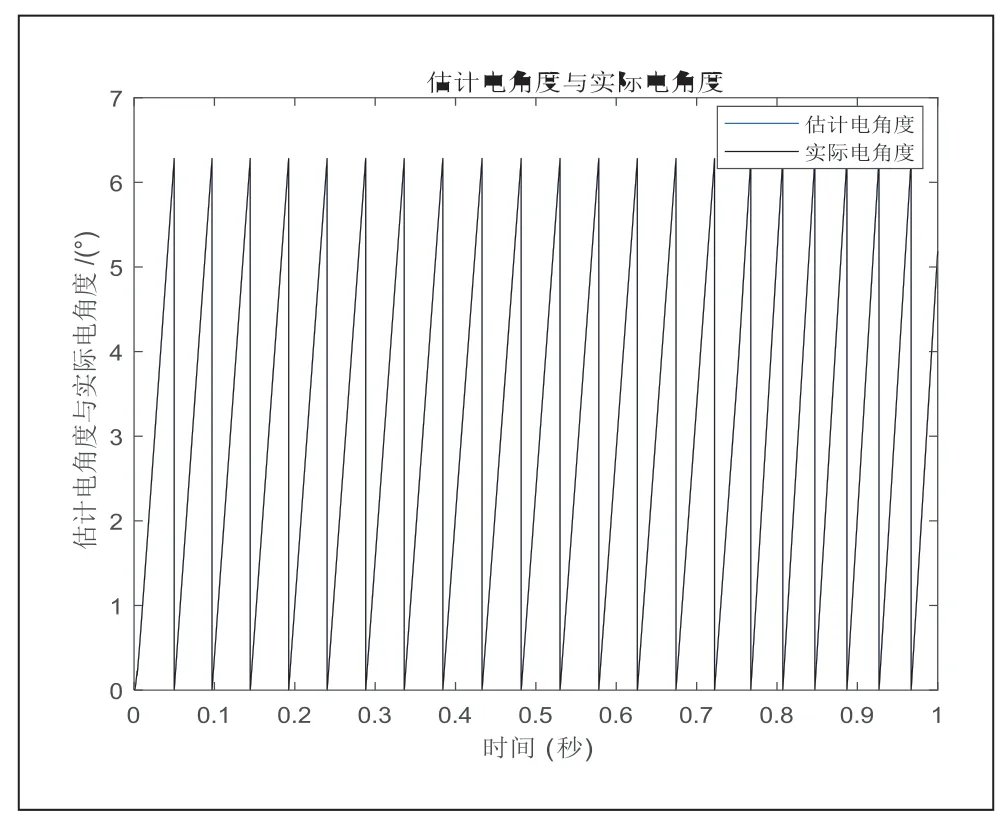
图6 STSMO-HFI 位置
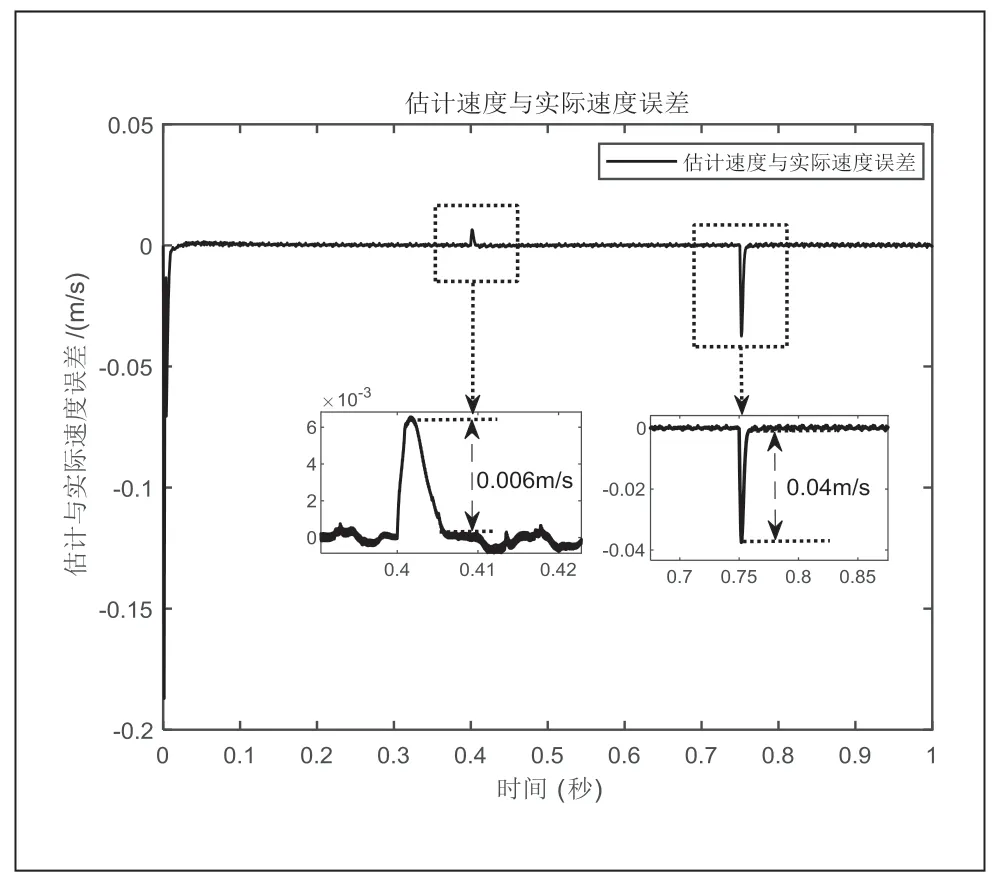
图7 STSMO-HFI 速度误差
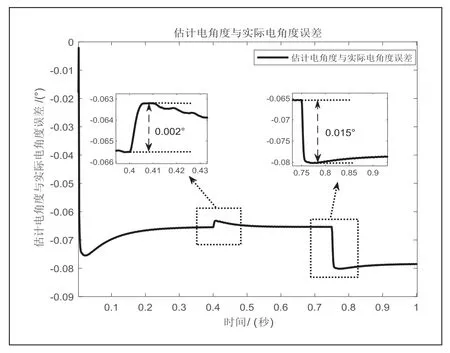
图8 STSMO-HFI 位置误差
仿真结果表明,PMSLM 能瞬间起动,STSMO-HFI 法瞬时误差最大达0.18m/s;突加负载后,0.005s 后预估速度可跟随实际运动速度;当PMSLM 进入速度的切换区间时,瞬时误差略微增大,速度误差和位置误差分别达到0.006m/s 和0.0015°,传统机械位置传感器速度误差达到0.08m/s,电机带上100N 负载运行后,传统机械传感器的电机达到期望速度的调整时间约为0.1s,STSMO-HFI 的调整时间为0.05s。
综上所述,利用高频注入法、超螺旋滑模观测法、复合滞环法可实现在两种算法之间平滑切换,较好预估PMSLM的运行情况。因此,充分利用两种算法的各自优势,实现无位置传感器速度和位置情况精确的估计。

