有机发光材料玻璃化转变温度与结构定量关系研究

禹新良，李明旺，吴旨进，谢 健，黄小可，黄赛金

（湖南工程学院 材料与化工学院，湘潭 411104）

0 引言

有机发光二极管（OLED）已经应用于商业展示，被认为是下一代照明技术重要的候选材料［1-2］.OLED 面板结构通常由阳极、空穴注入层、空穴传输层、有机发光层、电子传输层、电子注入层、阴极及基板组成.发光层是OLED 的核心部件，有机发光材料能将电子转换成光源［3-4］.

热应力对OLED 器件性能的影响还未得到广泛研究［5-6］.OLED 受到的热应力来自设备运行或外部环境，有报道表明暴露在较高温度的环境中可能导致OLED 性能的显著下降［6-7］.OLED 性能在热应力下的退化可能与发光层出现从玻璃态向高弹态转变，继而使器件层形貌结构发生改变有关.因为形貌结构的变化会导致电荷注入和传输的不平衡，从而减少激子的形成、影响辐射衰减［8-10］.因此，为了实现OLED 器件的稳定，有必要发展高玻璃化转变温度（Tg）的OLED 器件发光层有机材料［9-10］.

玻璃化转变温度（Tg）是材料从玻璃态向高弹态转变的温度.Tg值可以通过各种实验技术测定，如差示扫描量热法（DSC）、热机械分析（TMA）和动态机械分析（DMA）.不同的测量可能会得出不同的结果，例如，DSC 方法在测量BNpA-1T 的Tg中，Tg值可以取为360 K、364 K、369 K，分别对应于玻璃化转变温度DSC 曲线中的起始点、中点、终点［11］.此外，在DSC 测量中，所获得的Tg值还受到加热速率等其他因素影响.

定量结构-性能关系（QSPR）模型可用于估算材料的Tg值.QSPR 研究基于的假设是分子结构决定分子的性质，具有相似结构的分子具有相似的性质.QSPR 的主要目标是基于统计方法建立分子结构参数与性质的定量关系式及模型.一旦模型得以建立，就可以预测分子的性质，哪怕是实验室尚未合成的物质［11］.

已有学者采用QSPR 模型对OLED 中有机发光材料Tg进行了预测.YIN 等［12］、XU 等［13］分别建立了有机发光材料Tg的含6 个分子参数和5 个分子参数的QSPR 模型.使用线性回归方法建立的两个模型都较精确，R2分别为0.927 0［12］和0.930 4［13］.Barbosa da Silva 等［14］利用支持向量机（SVM）算法建立了66 种有机发光材料logTg的QSPR.该模型虽然精确（R2=0.962 6），但模型包含的分子参数（m=20）太多，因为在QSPR 研究中要求样本（n）和分子参数（m）之间的比率（n/m）应该大于5，显然该模型不满足此要求.QSPR 模型中使用的分子参数过多可能会增加模型的复杂性.最近，Zhao 等［11］构建了一个包含1 944 种有机发光材料Tg的QSPR 模型.使用LightGBM 算法开发的模型，其均方根误差为24.63 K，决定系数R2为0.77.虽然模型精确性有待提高，但所建模型具有统计意义.本文将采用随机森林回归方法建立以Tg/MW作为因变量更为精确的QSPR 模型.

1 材料与方法

从文献［11］得到1 944 种有机发光材料及其Tg值.将Tg值转换成Tg/MW值（MW为化合物分子量），按照该值大小进行升序排列，新序号是5 的倍数的样本作为测试集（n=388），剩余样本为训练集（n=1 556）.从训练集得到QSPR 模型，测试集对模型进行检验.

采用ChemDraw Ultra 8.0 软件构建分子的二维结构，用Chem3D Ultra 8.0 将其转换成3D 结构，并采用其中的AM1 方法对分子结构进行优化.最后采用Dragon 6.0 对分子进行参数计算，每个分子分别计算4 885 个分子参数.对那些参数值接近常数或偏相关性系数大于0.9 的参数予以剔除，最终得到472 个分子参数用于逐步回归分析.

2 结果与讨论

以计算所得的472 个分子参数作为自变量，1 944 种样本的Tg/MW作为因变量，用SPSS 19.0 对它们进行逐步回归分析.表1为模型概要，以R2≥0.005作为模型引进新参数标准，得到7 个分子参数，其定义见表2.基于所得参数子集，从训练集得到线性模型，决定系数R2为0.874，模型系数见表3.然后对测试集388 个样本进行预测，其相关系数R2为0.875.测试集与训练集R2值接近，模型不存在过拟合问题.此外，所得模型决定系数R2＞0.87，大于文献报道值R2=0.77，且大于模型接受标准R2＞0.5，具有统计意义.Tg/MW实验值与线性模型计算值关系如图1所示.

图1 Tg/MW实验值与线性模型计算值关系图

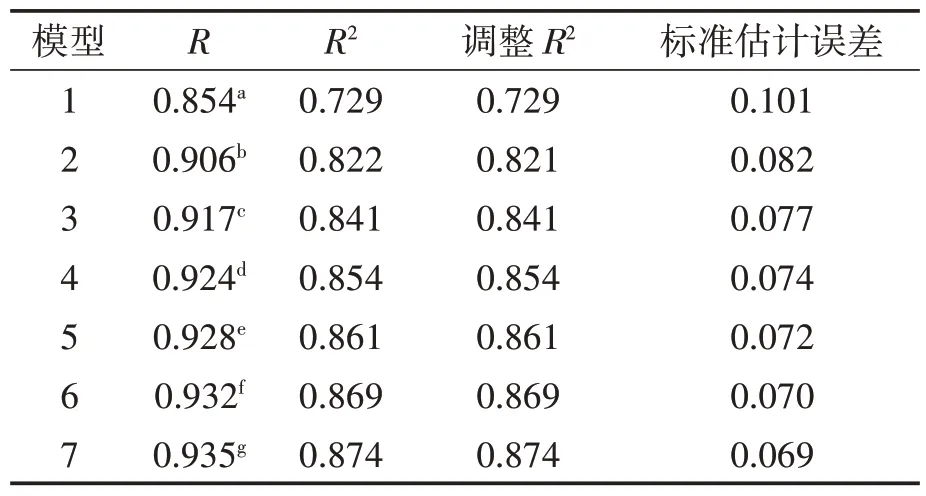
表1 模型概要

表2 挑选的分子参数、类别及定义

表3 模型系数

考虑到分子结构参数与因变量Tg/MW可能存在非线性关系，本文采用随机森林回归建立它们的非线性模型.基于程序包RandomForest 在MATLAB R2014a 平台运行得到［15-16］.由于参数nodesize（决策树节点的最小个数）一般对模型预测性能影响不大，本文取其默认值（nodesize=5）.先固定mtry（构建决策树分支时随机抽样的变量个数）=2，决策树数目ntree从100 变动到600，步长为100，结果显示ntree=200，mtry=2 时产生的结果较理想.接着，固定参数nodesize=5，ntree=200，从1 变化到6，步长设置为1.最终结果显示，nodesize=5，ntree=200，mtry=2 为最佳模型参数，所得随机森林回归模型产生的训练集R2=0.979，测试集R2=0.893，高于线性回归结果.因此，本文所用分子结构参数与因变量Tg/MW确实存在非线性关系.实验与随机森林模型计算Tg/MW值关系如图2 所示.

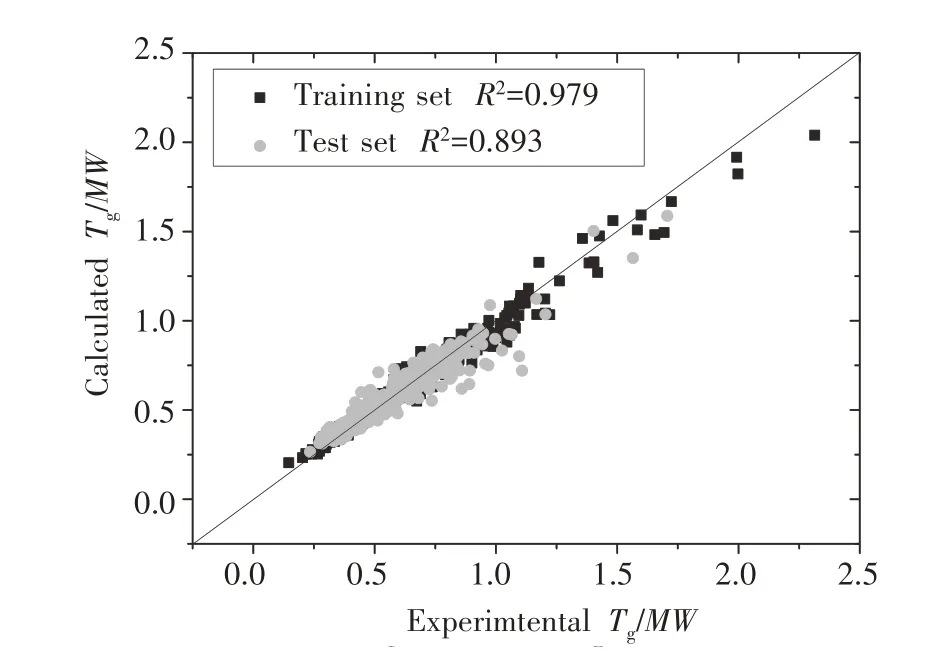
图2 Tg/MW实验值与随机森林模型计算值关系图

比较图1 与图2 可以发现，图2 散点更接近对角线，意味着随机森林模型预测值更准确.

|t|值大小反映参数对因变量Tg/MW的贡献程度.根据表3中的t检验，参数 ||t值按照以下顺序递减：HATS4i、SM04-AEAdm、R2i、RBN、Chi-DDt、SpMax5-Bhm、Yindex，它们的显著性也是照此顺序递减.表3 显示，所有参数的Sig.值（p值）均小于0.001，接近0，表明参数均为显著性参数；另外，参数的膨胀因子VIF值小于10，表明参数间共线性问题不严重.

参数SM04_AEAdm是基于偶极矩加权的、从边缘邻接矩阵计算得到的4 阶谱矩.该参数能反映分子碎片图连接方式.参数SM04-AEAdm越大，表明分子体积越大，链的旋转就越困难，分子玻璃化转变温度越高.另一方面，分子体积越大，其分子量也越大，MW值越大，从而Tg/MW值降低.因此SM04-AEAdm与Tg/MW相关.

参数RBN定义为分子中旋转键的数目，该参数能反映分子单键数目，但不包含C-N 单键，因为其具有高的旋转势能.分子旋转单键数目越多，分子柔性越好，玻璃化温度就越低，因而RBN与Tg/MW负相关.

参数HATS4i能反映分子中原子i与j之间相互作用、分子对称性等信息，并且能反映同系物中分子的差异.而对称性是影响分子玻璃化温度的一个重要因素，对称性越好，分子旋转越容易，Tg越低.因此Tg与HATS4i负相关.

参数Chi_DDt基于分子图理论，从距离矩阵导出.Chi_DDt能反映分子成环信息.通常分子的环结构如苯环、苯并噻唑、苯并噁唑都是刚性环.这些环结构的存在能增加分子的玻璃化转变温度Tg.因此，Chi_DDt与Tg正相关.

参数SpMax5_Bhm基于分子键序与分子图的Burden矩阵.该类参数常用于描述大数据集中分子相似性或差异性.SpMax5_Bhm与参数SM04_AEAdm类似，较大的SpMax5_Bhm值表示分子体积越大，从而影响分子的旋转，并增大玻璃化转变温度Tg.

参数R2i与HATS4i类似，同属于GETAWAY（GEometry，Topology，and Atom-Weights AssemblY）参数，反映分子形状与大小.但参数R2i反映分子几何、拓扑图中原子之间的距离.分子量MW越大，经电离势加权的R2i越大.由于R2i反映的特征如基团或碎片如-C（=O）N-在空间的有效位置，而这些基团属于刚性基团，从而影响分子的玻璃化转变温度Tg.

参数Yindex能反映分子在空间的拓扑距离.与HATS4i相似，能反映分子中原子i与j之间相互作用、分子对称性等信息.较小的分子如（No.513）CCCC（C）（C）［Si］（C）（C）N1C（=O）C=CC1=O 及样本（No.1591）CC（C）（C）［Si］（C）（C）N1C（=O）C=CC1=O，对称性低，但其玻璃化转变温度Tg却高，分别为477.15K、489.15K.

3 结论

本文将1 944种用于OLED 的有机发光材料分成训练集和测试集.从训练集（1 556 种）得到的线性回归方程决定系数R2=0.874，测试集（388 种）R2=0.875.而基于随机森林回归模型（nodesize=5，ntree=200，mtry=2）产生的训练集R2=0.979，测试集R2=0.893，分别高于线性回归模型结果，表明所选参数与Tg/MW存在非线性关系.且本文模型精度均高于文献报道值，表明所选参数能反映影响Tg/MW或Tg的结构因素.