一个关于矩阵秩的恒等式及其应用

杨 森,赵 丹

(鞍山师范学院 数学学院,辽宁 鞍山 114007)

本文用r(A)表示矩阵A的秩.文献[1]证明了对于任意的m×s矩阵A及s×n矩阵B,都有r(AB)≤r(B).因此,r(B)-r(AB)是一个非负整数.这个结论并没有指出如何准确估计r(B)-r(AB)的值,本文将深入探讨这个问题.

首先,引入线性映射的概念及其基本定理.

(i)对任意的α,β∈V,都有

(ii)对任意的α∈V和k∈P,都有

线性空间V上的线性变换是从V到V的线性映射,因此线性映射是比线性变换更广义的概念.

事实上,这个基本的数量关系对于线性映射仍然成立,文献[2-3]中有关于这个基本数量关系的论述.为了论述的完整性,本文给出它的证明.

k1β1+…+kmβm=s1α1+…+snαn

由向量组α1,…,αn,β1,…,βm的无关性,可得

k1β1+…+kmβm-s1α1-…-snαn=0

所以

证毕.

线性映射的典型例子是由矩阵给出的.设A是数域P上的一个m×n矩阵,不难验证从Pn到Pm的映射xAx是个线性映射.我们仍用A表示这个线性映射.齐次线性方程组Ax=0的解空间是Pn的子空间,它就是线性映射A的核;矩阵A的列向量都是m维向量,A的所有列张成的子空间是线性映射A的像.定理1说明这两个子空间维数之和等于n,这正是齐次线性方程组的基本数量关系.

应用线性映射基本定理(定理1),可推出本文的有关矩阵秩r(B)-r(AB)的主要定理:

菊花当然不能说话，所以这个主人公和菊花的对话实际上是主人公自己和自己的对话。自己才是菊花本身，即使在监牢里，不能吸收养分，花朵变得越来越小，也有要开出有着象牙般光泽的花朵的心。最后，“我把这件事，写在了给我那身体很小的母亲的信中。”主说：“你们祷告的时候，不可像那假冒为善的人，爱站在会堂里，和十字路口上祷告，故意叫人看见。”只有一切只是在自己的心里发生的变化才是自己的真实。主人公在监狱中，通过在心中和自己的对话，坚信自己所做的事是正确的，然后把这决心传达给了自己的母亲。

定理2给定数域P上m×s矩阵A及s×n矩阵B,则

r(B)-r(AB)=dim (V1∩V2)

其中:V1为齐次线性方程组Ax=0的解空间,V2为矩阵B的列向量生成的子空间.

定义

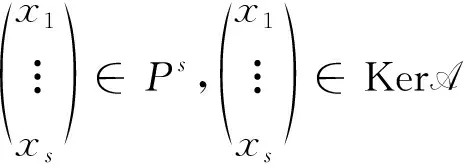
dimV2=dim (V1∩V2)+dimV3

其中V3是矩阵AB的所有列向量生成的Pm的子空间.而

dimV2=r(B),dimV3=r(AB)

所以

r(B)=dim (V1∩V2)+r(AB)

由此得到定理2的结论.证毕.

定理2回答了本文最开始要解决的重要问题,即给出了r(B)-r(AB)的准确估计.利用这个估计,关于矩阵秩的Sylvester不等式[4]和Frobenius不等式[5]都可以获得更简洁的证明,这样,很多有关矩阵秩的不等式问题迎刃而解.下面,利用定理2给出这两个重要不等式的新的证明过程.

定理3(Sylvester不等式)设A为m×n矩阵,B是n×k矩阵,则

r(AB)≥r(A)+r(B)-n

证明由定理2,有

r(B)-r(AB)=dim (V1∩V2)

(1)

其中:V1是齐次线性方程组Ax=0的解空间,V2是矩阵B的列向量生成的线性空间.

由定理1,有

n-r(A)=dimV1

(2)

而

dim (V1∩V2)≤dimV1

综合式(1)与式(2)即得所要证明的不等式成立.证毕.

由此证明还可以给出Sylvester不等式中等号成立的条件,即

dim (V1∩V2)=dimV1

这等价于V1为V2的子空间,这就证明了下面的推论:

推论1设A为m×n矩阵,B是n×k矩阵,则

r(AB)=r(A)+r(B)-n

的充要条件是齐次线性方程组Ax=0的解均为B的列向量组的线性组合.

定理4(Frobenius不等式)设A,B,C分别为m×n,n×s,s×k阶矩阵.则

r(B)+r(ABC)≥r(AB)+r(BC)

证明由定理2,有

r(B)-r(AB)=dim (V1∩V2)

(3)

其中:V1是齐次线性方程组Ax=0的解子空间,V2是矩阵B的列向量生成的线性空间.

再由定理2,有

r(BC)-r(ABC)=dim (V1∩V3)

(4)

其中:V1是齐次线性方程组Ax=0的解空间,V3是矩阵BC的列向量生成的线性空间.而BC的列都是B的列的线性组合,所以V3是V2的子空间,由此可知

dim (V1∩V3)≤dim (V1∩V2)

(5)

综合式 (3)、(4)、(5)即得所要证明的不等式成立.证毕.

相比传统的利用矩阵分块法给出的证明,本文给出的证明含义更加清楚.根据定理2给出的关于r(B)-r(AB)的准确估计,可以简洁有效地导出更多关于矩阵秩的不等式.