梁场仓储装备智能集群控制系统中运梁车调度研究
肖浩,毕鹤鸣,李国锋,冷志坚,易飞
(1.中交第二航务工程局有限公司,湖北 武汉 430040;2.中国交通建设集团有限公司,北京 100088;3.长大桥梁建设施工技术交通行业重点实验室,湖北 武汉 430040;4.交通运输行业交通基础设施智能制造技术研发中心,湖北 武汉 430040)
0 引言
梁场仓储装备智能集群控制系统在桥梁建设领域扮演着至关重要的角色。运梁车作为其中的核心装备之一,其调度对于提高施工效率和减少成本具有重要意义。传统的运梁车调度通常依靠人工经验和简单的规则,效率较低且容易出现问题,而随着工程规模的扩大和施工难度的增加,传统的调度方法已经无法满足实际需求。
本文将针对梁场仓储装备智能集群控制系统中的运梁车调度问题进行深入研究[1-3]。将基于现有的智能调度算法和技术,结合梁场仓储装备的特点和需求[4-6],提出一种高效、智能的运梁车调度方法。通过优化调度方案,本文旨在实现运梁车的最大利用率,减少空闲时间和资源浪费,从而提高施工效率和降低成本。
1 工程概况
梁场仓储装备智能集群控制系统运梁车调度研究依托于某高速改扩建工程。该工程梁场场地布置图如图1 所示。
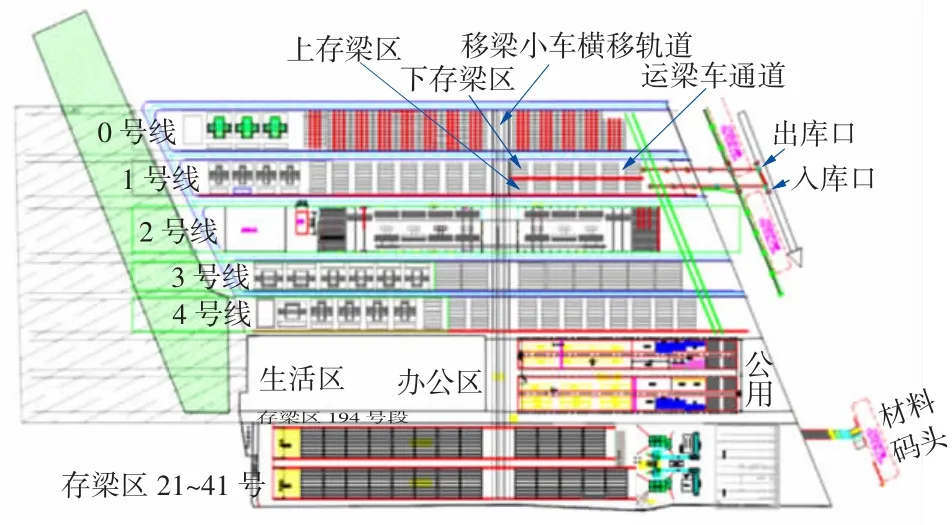
图1 某扩建工程梁场场地布置图Fig.1 Layout diagram of the beam yard for a certain expansion project
如图1 所示,该预制梁场包含入库口、出库口、上存梁区、下存梁区、节段梁预制区及运梁车通道组成。
梁场施工装备集群控制系统根据人工智能规划算法实现设备的智能调度[7-8]、仓位的合理分配、危险区域的自动避让及路径优化等功能,自主完成移梁、存梁、取梁、倒运等工作,达到自主决策、自动执行、实时跟踪为一体的信息流与实物流高度一致的梁场施工装备集群控制系统[9]。
2 梁场仓储布局图与运梁车路径策略选择
梁场的仓储系统主要包括存梁区、运梁车和控制系统。存梁区是用来储存节段梁的,每条梁道上都有若干个空间,表示若干个储存的梁位,一条存梁巷中只可储存一种类型的节段梁;运梁车是用来实现节段梁体的水平运转;控制与管理系统主要是对仓库中的设备进行监视与调度。
图2 是一种运梁车仓储系统的布置图。位于中央主要道路之上的被称作上存梁区,而位于中央主要道路之下的被称作下存梁区。在此存储系统中,进出料提升装备设置在进出入口。运梁车可在存梁巷道横、纵2 个方向移动。在无货物的情况下,运梁车能在存梁巷道内自由地移动,并能抵达仓库系统内任何一个存梁位置。

图2 运梁车仓储系统的布置图Fig.2 Layout diagram of the beam transportation vehicle warehousing system
在运梁车仓储系统中,由于多辆运梁车辆同时工作,会在主要道路的交叉路口和通道中发生碰撞和卡死,从而造成存梁区的拥堵,影响出入库作业的顺利进行。因此,在求解该问题时,如何有效地避免运输车辆间的碰撞和卡死,是求解该问题的一个重要方面。
首先,建立存梁区交通网络模型,如图3 所示。先将其表示为图G={V(G),E(G)},图G里所有点的集合为V(G),所有边的集合为E(G)。其中主要道路、车道等被等价于图G中的边,十字路口被等价于点。利用Hopcroft-Tarjan 算法,对无割边的连通图G进行了计算,得出了图G的强连通方向图,其步骤如下:

图3 存梁区交通网络路径定向图(图G)Fig.3 Directed graph of traffic network paths in beam warehousing district(Fig.G)
第一步:在图G中任取某顶点v,使得l(v)=1,L={v},U=V-{v}且R=Ø;
第二步:从L中选取1 个顶点u,其中l(u)的值是最大的;同时,确保在U中存在1 个与u相邻的顶点w。然后从U中选择1 个与u相邻的顶点w,并将边uw转变为有向边u→w;接着,设置l(w)的值为l(u)+1,将w加入L,从U中移除w,并将u→w加入A中;
第三步:如果L≠V,则进入第二步,否则,进入第四步;
第四步:对于目前尚未定向的边ab,根据下面的方式进行定向:如果l(a)>l(b),那么指定方向后的边为a→b,反之,边为b→a。
其中,U是尚未给出标号的顶点集,L是已给出标号的顶点集,R是方向已确定的边的集。
根据上述求解步骤,在图G中出现多个强连通定向图,需在此基础上,结合梁场布局和出入库原则,确定最终路径定向路径选择方法。
3 运梁车调度算法研究及应用
在梁场的仓储设备调度中,本文结合了模拟退火算法在局部搜索中的优势,提出了一种新的混合遗传算法(IH-GA)。这种算法既继承了遗传算法在全局搜索中的高效性,又融合了模拟退火算法在局部寻优中的强大能力。
IH-GA 的操作机制如下:首先,通过GA 对初代种群执行遗传处理,以实现种群的进化。接着,利用模拟点火算法中的Metropolis 采样方式,对由遗传算法进化得来的结果进行评估和抽样。这些抽样的结果将再次作为遗传算法的起始种群,为下一轮的进化做准备。
将该算法应用到运梁车调度上,首先需对运梁车调度问题进行建模,仓储系统中运梁车的作业调度问题可以数学化描述为:由m台运梁车来完成n个存梁出入库任务的分派,全部任务集A={A1,A2,…,Am},运梁车集S= {s1,s2,…,sm},第i台运梁车的任务集Ai= {a1i,a2i,…,aki}。基于约束条件,合理地规划运梁车的任务分派和执行顺序。以下是约束条件的构建:
式中:ki为第i台运梁车分配的任务总数量,式(1)表示每辆运梁车至少指派一个任务。
式(4)表示所有的工作都由运梁车来完成。
式(5)表示一项任务仅可通过一个运梁车来完成。
在上述约束模型的基础上,建立了以下目标函数:为了确定多台运梁车完成出入库任务的最短
时间,也就是实现所有运梁任务的时间最小化,考虑编号为i的运梁车完成ki个任务的操作时长Ti如下:
式中:sPosj为编号为j的任务起点;ePosj为编号为j的任务终点。
运梁车的工作时间取决于具体的工作任务,并与车辆的起点和梁的位置相关,基于以上的路径定位策略,对运输路线进行规划,并对运输时间进行计算。在进库工作中,运梁小车从起点出发,行驶到进库入口,再按照存梁区的路径导向策略,规划出一条路线,从进库入口一直行驶到目标梁位。入库任务作业示意图如图4 所示,其空载阶段运行时间为:

图4 入库作业示意图Fig.4 Warehouse entry operation diagram
式中:(xe,ye)为目标货位坐标;(xs,ys)为运梁车停靠点坐标;w为单个货位宽度;l为单个货位长度;tu为运梁车转向时间。
同理可得运梁车的出库作业建模。
将IH-GA 算法带入到该模型,并且使用GA算法和SA 算法作为对照组,其得到的在40、80、120 任务下的平均完成时间、平均偏差与优化效率如表1 所示。

表1 3 种算法实验结果对比Table 1 Comparison of experimental results for 3 algorithms
与GA 算法和SA 算法相比,IH-GA 算法具有更高的计算效率、计算精度、稳定性和更快的计算速度。随着任务规模的增加,出入库任务分配及运梁车执行序列变得更加复杂,与GA、SA等算法相比,IH-GA 在计算精度、稳定性等方面的优势得到了放大,其优化表现更为出色,进出库任务的分配和运梁车的执行次序变得更加有序,任务的总完成时长缩短了,从而提高了工作效率,因此,IH-GA 算法更适合于解决大规模的调度优化问题。
图5 展示了GA、SA 和IH-GA 三种算法在不同任务规模时的收敛情况。在开始阶段,GA 算法展现出了优秀的全局搜索性能,具有很好的收敛性,但是由于其局部寻优能力较差,使得其解的精度较低;SA 算法具有很好的寻优性能,但存在着寻优时间长、收敛缓慢等缺点;IH-GA 算法融合GA、SA 的优势,在GA 的基础上,充分发挥GA 的全局寻优能力,使其在初始阶段就能达到较快的收敛性,并且将SA 的局部寻优能力相结合,使其在初始阶段就能达到较快的收敛性与较好的收敛性。与其它2 种方法相比,该方法不仅具有较高的计算精度,而且具有较快的收敛性,因此该方法更适用于该模型的优化问题。

图5 3 种算法在不同任务规模下的算法收敛图Fig.5 Algorithm convergence graphs for 3 algorithms at different task scales
当处理任务规模达到40 时,通过IH-GA 算法的优化,实验得到了5 台运梁车的任务执行顺序,见表2。

表2 优化后运梁车分配的专业任务及执行顺序Table 2 Optimized professional task and execution sequence assigned by beam transportation vehicle
这5 台运梁车的操作时间分别为420.36 s、421.92 s、427.26 s、424.63 s 和428.59 s。任务的总完成时间为428.59 s。优化之后,第5 台运梁车的工作路径如图6 所示。而第5 台运梁车的作业路线是:(1,1)→(22,44)→(0,0)→(11,6)→(31,11)→(0,60)→(0,0)→(41,33)→(0,0)→(70,15)→(0,0)→(43,21)→(65,24)→(1,60)→(56,38)→(0,60)。

图6 优化后第5 台运梁车出入库专业路径图Fig.6 Optimized path diagram for entry and exit of the 5th beam transportation vehicle in the warehouse
从上述分析中可以看出,通过优化混合遗传算法的编码方法和变异修复策略,成功地解决了在迭代中容易产生的非法解问题,扩大了解的多样性,并增强了算法的快速收敛特性和全局搜寻效率。
4 结语
本论文主要对运梁车存储系统的调度优化进行了研究。基于Hopcroft-Tarjan 算法,研究存梁区的路径定向策略,构建基于最短运梁时间的调度优化模型,研究基于Hopcroft-Tarjan 的多目标优化问题。实验结果表明,该方法能有效地解决车辆的碰撞和卡死问题,提高了系统的运行效率。为了比较计算法的性能,将IH-GA 算法与GA 算法、SA 算法的计算结果进行了对比。通过算例分析,证明了IH-GA 的寻优性能好,收敛速度快,可大幅提高系统工作效率。

