基于动力学守恒定律的弹道目标关联方法

曾舒雅, 饶 彬

(中山大学电子与通信工程学院, 广东 深圳 518107)

0 引 言

弹道导弹是现代战争中威力极大的武器,具备射程远、速度快、精度高、突防能力强、效费比高等优点[1]。弹道导弹的飞行包括3个阶段,即助推段、中段和再入段。其中,中段是识别和拦截弹道导弹的重要阶段。为了提高弹道导弹的突防能力,通常会采取多种突防措施,主要有释放诱饵或箔条、末修舱爆炸产生碎片、有源干扰等[2]。由于弹道导弹在中段飞行期间处于距离地面几十至上千千米的高空,大气稀薄,空气阻力可以被忽略,可看作只受地球引力影响,诱饵、箔条、碎片等会伴随弹道导弹高速飞行,且数量巨大。各目标的空间分布密集,运动状态相似,从而形成突防云团[3]。对雷达系统而言,这是典型的密集多目标环境,雷达对目标的识别和跟踪都会因此而受到极大影响。

为了有效实现对弹道目标的防御,地面跟踪雷达须具备较高的跟踪精度。针对空间密集群目标的数据关联问题,国内外有诸多研究。文献[4]提出基于双向互选的群目标关联方法,改善了密集目标环境下关联可能存在的“先占先得”的问题,防止航迹混批。文献[5]提出基于贝叶斯框架的空间群目标关联方法,构造群中心跟踪的贝叶斯过程,在以群目标整体为跟踪对象的同时兼顾个体目标的跟踪,提高跟踪精度。文献[6]将弹道群目标关联问题看作一个最优分配问题,根据目标的距离、速度、航向等特征参数建立分配矩阵并进行求解。现有方法多立足于关联算法的改进或弹道群目标的空间特性,而未考虑弹道目标的运动学特性。

常用于目标跟踪关联的算法有最近邻数据关联(nearest neighbor data association, NNDA)算法[7]、概率数据关联(probability data association, PDA)算法[8]、联合PDA(joint PDA, JPDA)算法[9]、多假设跟踪(multiple hypothesis tracking, MHT)法[10]。其中,JPDA和MHT复杂度高、计算量大,不适合实际应用。NNDA虽然计算量小,但极易产生关联错误。PDA计算量较小,便于工程应用,但在目标密集的环境下,大量干扰落入关联波门,仍然容易发生关联错误的情况,从而导致航迹断裂或混批。

针对上述情况,本文将弹道目标的运动学特性与PDA方法相结合,提出一种适用于中段弹道目标跟踪的基于动力学守恒定律的关联方法。中段弹道目标的动力学守恒特性包括动量矩守恒特性和机械能守恒特性。本文提出的关联算法在使用传统关联门得到有效量测的基础上,对动量矩和机械能做联合统计检验以进行进一步筛选,并用动量矩和机械能对用于加权的关联概率进行修正。通过蒙特卡罗仿真,验证了与传统PDA方法相比,本文提出的方法能够取得更强的抑制干扰和杂波影响的能力,从而获得更高的跟踪精度。

1 中段弹道目标的动力学守恒问题

1.1 运动模型

1.1.1 实体目标

目标单位质量动量矩的计算公式为

(1)

动量矩的值为

(2)

目标单位质量机械能的计算公式为

(3)

1.1.2 有源假目标和杂波

在有源干扰中,应用最多的是有源距离欺骗干扰。有源距离欺骗干扰是指有源干扰机接收到真目标点迹后将其转发生成假目标点迹,从而干扰探测雷达[14]。一个延时Δt后转发的有源距离欺骗假目标的延迟距离Δr=cΔt/2,其中c为光速[15]。若真目标在以雷达站为中心的球坐标系下的位置矢量为(r,θ,φ)T,则假目标在此坐标系下的位置矢量为(r+Δr,θ,φ)T。

除实体目标和有源假目标外的其他量测被视为杂波。杂波相互独立并服从空间均匀分布,且杂波数量服从泊松分布[16]。

文献[17]证明,实体弹道目标满足动力学守恒定律,而杂波和有源假目标则不满足。因此,可以在跟踪中利用这一特性,避免杂波和有源假目标的干扰。

1.2 坐标系转换

1.2.1 球坐标系到ENU坐标系的转换

球坐标系到ENU坐标系的转换公式为

(4)

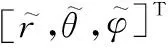
(5)

式中:

其协方差矩阵为

(6)

式中:

式中:

1.2.2 ENU坐标系到ECI坐标系的转换

ENU坐标系到ECI坐标系的位置转换公式[12]为

re=T[r+(0,0,ro)T]

(7)

速度转换公式为

(8)

式中:ro为地球平均半径;T为变换矩阵,其表达式为

其中,L和B为雷达站位置的经度和纬度。

2 基于动力学守恒定律的改进PDA方法

假设航迹起始已经完成。基于动力学守恒定律的改进PDA方法的算法流程如图1所示。

图1 算法流程图Fig.1 Algorithm flowchart

文献[22]指出,对弱非线性的弹道目标,扩展卡尔曼滤波(extended Kalman filter, EKF)有较好的性能和较小的计算量。因此,以EKF为例,算法具体步骤如下:

步骤 1f为状态方程,h为量测方程,F和H分别为f和h的雅可比矩阵。Δt为时间间隔。Q和R分别为过程噪声协方差矩阵和量测噪声协方差矩阵。

在k时刻,使用EKF算法得到目标的预测状态:

(9)

预测位置为

(10)

预测协方差为

(11)

式中:

滤波增益为

(12)

式中:

步骤 2用传统关联门筛选出有效量测:

(13)

式中:m(k)为k时刻有效量测的个数;γ为关联门门限。

步骤 3对每个有效量测进行无偏转换,并求动量矩和机械能及其方差。

(1) 无偏量测转换

则Zce的协方差矩阵Rce由下式求得:

(14)

(2) 预测速度转换

(15)

(3) 求动量矩和机械能及其方差

使用雷达获取的量测位置和滤波得到的预测速度计算动量矩和机械能及其方差。则由式(1),对第i个有效量测,动量矩分量可表示为

(16)

对h进行全微分,得到其3个分量的方差:

(17)

与位置之间和速度之间的协方差相比,位置与速度之间的协方差非常小,因此可近似为0。于是,式(17)可简化为

(18)

动量矩的方差值为

(19)

由式(3),机械能由下式计算:

(20)

对E进行全微分,得到其方差:

(21)

与上述动量矩方差的计算同理,位置与速度之间的协方差可近似为0,故简化后为

(22)

机械能的方差值为

(23)

步骤 4对所有有效量测进行动量矩和机械能的联合统计检验。

(1) 估计动量矩和机械能守恒值

因为实体目标的动量矩和机械能在整个跟踪过程中守恒,故有

(24)

(25)

(2) 建立动量矩和机械能的联合统计检验模型

对动量矩建立统计检验量为

(26)

定义假设:

判决方法:

对机械能建立统计检验量为

(27)

检验方法与动量矩同理。

设Dh为动量矩的检验结果,Dh=1表示真目标点迹,Dh=0表示干扰点迹。DE为机械能的检验结果。综合检验结果D=Dh∩DE。当且仅当D=1,即动量矩和机械能都守恒时,才认为第i个有效量测是真目标点迹并保留,否则认为其为干扰点迹并剔除。本文取α=0.001。

步骤 5计算余下量测来自被跟踪目标的关联概率,加权形成等效量测并更新目标状态。

(1) 计算关联概率

记k时刻经步骤4后余下量测的个数为n(k)。量测j为真目标点迹的概率[16]为

(28)

式中:

(29)

b=λ(1-PDPG)

(30)

j=0表示没有正确量测;PG为正确量测落入关联门的概率;PD为目标被检测到的概率;λ为杂波密度。相比传统的PDA方法,本文提出的方法利用动量矩和机械能对关联概率作了如式(29)所示的修正。

(2) 更新目标状态

k时刻有效量测j的新息为

(31)

则形成的等效量测的新息为

(32)

用等效量测更新目标状态:

(33)

更新协方差:

(34)

式中:

Pc(k)=P(k|k-1)-W(k)S(k)W′(k)

k时刻目标的瞬时动量矩h(k)和机械能E(k)由更新后的状态X(k)计算得到。

算法流程用伪代码表示,如算法1所示。

算法 1 基于动力学守恒定律的改进PDA方法输入 初始状态、量测值、量测噪声方差、过程噪声方差1: for k=1:观测持续时间 2: 计算预测位置3: for j=1:量测数4: if 量测j落入关联门5: 量测j为有效量测6: else7: 剔除量测j8: end if9: end for10: 估计动量矩和机械能守恒值11: for i=1:有效量测数12: 对有效量测i进行无偏转换13: 计算有效量测i的动量矩和机械能及方差14: 做动量矩和机械能联合统计检验15: if 通过统计检验16: 保留有效量测i17: else18: 剔除有效量测i19: end if20: end for21: 计算余下量测的关联概率22: 加权形成等效量测并更新目标状态23: end for

3 仿真验证

仿真跟踪场景如下:假设已经完成航迹起始。真目标关机点高度为80 km,关机点速度为2 500 m/s,中段总飞行时间为370 s。雷达布站的位置为北纬1°,东经1.5°,跟踪数据频率为1 Hz。雷达距离量测噪声标准差为20 m,角度量测噪声标准差为10-4rad,过程噪声方差取0.02 m2·s-4。每帧数据中含有一个带噪声的真目标量测和10个电假目标量测,延迟距离为50 m到500 m,相邻电假目标的延迟距离均相差50 m。同时,跟踪过程中伴有杂波,密度为10-8m-3。PDA算法中的关联门门限为128。目标检测概率为1,正确量测落入关联门的概率为0.999。

图2展示了仿真跟踪场景。

图2 仿真跟踪场景Fig.2 Simulation tracking scenario

图3为传统PDA方法和本文方法的关联结果对比。图4为图3中两个虚线矩形框处航迹的局部放大。图4(a)为虚线矩形框1,即航迹末尾处的局部放大。由图4(a)可知,在既有杂波又有假目标的情况下,传统PDA方法会受到较明显的干扰,导致真目标航迹逐渐被假目标点迹带偏,出现了关联错误,而本文方法则避免了这种情况。图4(b)为图3虚线矩形框2处航迹的局部放大,目的是示例两级关联门对量测的筛选过程。动力学守恒检验相当于在传统关联门的基础上建立了第二级关联门,可以看到依据动力学守恒量建立的第二级关联门进一步剔除了远离真目标航迹的干扰量测,起到了抑制航迹被一系列假目标点迹“拉偏”的作用,从而将航迹向正确方向“拉回”。图3从左到右为时间t从0到400 s的目标轨迹。

图3 关联结果Fig.3 Association result

图4 关联过程Fig.4 Association process

进行1 000次蒙特卡罗仿真,对未失跟的情况做平均跟踪误差对比,如图5所示。可见相较于传统PDA方法,本文方法有效降低了跟踪误差,提升了跟踪精度。

图5 关联误差Fig.5 Association error

图6展示了动量矩和机械能的理论值和由1 000次蒙特卡罗仿真的关联结果计算得到的平均实际值。可以看到,传统PDA方法的动量矩和机械能偏离真目标理论值较远,且接近3σ限边缘或超过3σ限,而本文方法的动量矩和机械能虽然初始时有一定起伏,但远未超过3σ限,且随着时间增加逐渐稳定在真目标理论值附近。

图6 动量矩和机械能Fig.6 Momentum moment and mechanical energy

为了对算法性能做进一步的分析,本文对比了仅利用动量矩和仅利用机械能的关联误差。图7给出了1 000次蒙特卡罗仿真误差对比图。

图7 不同方法的关联误差对比Fig.7 Association error comparison of different methods

由仿真结果可知,仅利用动量矩或机械能都能够有效减小跟踪误差,且其误差小于传统PDA方法,但大于本文方法,即同时使用动量矩和机械能。该结果说明了本文方法的有效性。

4 结 论

本文针对中段弹道目标在有源距离欺骗干扰和杂波存在情况下的跟踪关联问题,利用中段弹道目标飞行期间满足动力学守恒定律的特性,提出一种用于中段弹道目标关联的改进的PDA方法。该方法能够有效减小有源距离欺骗干扰和杂波对目标跟踪关联的影响。仿真结果表明,该方法的性能优于传统PDA方法,能够减小跟踪误差,提升跟踪精度,具有工程应用价值。