基于灰狼算法的箔条幕干扰构设方法研究
裴立冠, 刘经东, 马春波
(中国人民解放军91550部队, 辽宁 大连 116023)
0 引 言
在现代海战场中,采取针对性电磁手段以有效干扰对方反舰导弹,对保护舰艇与人员安全、保证战斗力可持续性具有重要意义[1-3]。箔条幕干扰是当前使用较广泛的一种无源干扰方法,可干扰装配各种雷达导引头类型的反舰导弹,兼具遮蔽与迷惑功能,且价格低廉、操作简单,在未来战场中仍将发挥重要作用[4-6]。
当前已经有少量关于箔条幕干扰的公开报道:蔡万勇等[7]建立了大气环境下箔条运动轨迹模型及箔条幕扩散模型;高东华等[8]对箔条幕防御反舰导弹进行了原理论证和基础模型构建;白爽等[9]通过分析反舰导弹雷达导引头边搜索边跟踪的机制特点,提出了箔条幕干扰使用方法。然而,纵观当前研究成果,关于箔条幕干扰战术战法方向的研究仍停留于概念化层面,未宏观考虑风速、风向、补弹等因素导致的干扰失败的风险,同时对于不同空间场景下箔条幕干扰布放距离、不同箔条弹发射方向与位置等关乎箔条幕实际布设与干扰效果的关键点也未见科学化的定量模型。
为此,以箔条幕干扰为研究对象,首先在对其内在干扰机理进行分析的基础上构建干扰场景模型,然后综合考虑干扰有效性和战略资源损耗性等因素构建总体求解方法,通过建立约束条件、目标函数、补弹策略,采用改进的灰狼智能优化算法求取最佳布放方案,最后通过仿真实验方法对模型有效性及干扰效果影响因素进行分析。
1 布放模型构建与求解
1.1 干扰机理
箔条幕干扰的基本方式如图1所示,在导弹M与舰艇S中间一定位置发射数枚箔条弹(C1~C5),形成具有足够长度和厚度的箔条幕墙,以有效干扰对方反舰导弹末制导雷达跟踪,保护舰艇免受攻击[2]。H1为垂直轴线,H2为箔条幕实际布放轴线。箔条幕干扰作用发挥的本质包含两个方面:一是遮蔽作用,幕墙能够有效阻挡和衰减末制导雷达主动发射的电磁波和舰艇反射的电磁波,使末制导雷达无法探测到舰艇目标;二是质心拖引作用,当末制导雷达无法跟踪舰艇目标时,转而攻击箔条幕能量质心,舰艇通过有效机动,保证自身始终处于导弹攻击范围之外。

图1 箔条幕干扰原理Fig.1 Chaff screen jamming principle
在实际箔条幕布放过程中,需始终遵循以下原则:一是箔条弹发射时间,舰艇侦察到对方反舰导弹后立即发射(一般为反舰导弹末制导雷达开机时刻);二是箔条弹发射位置,需综合考虑风速、风向、舰艇机动等因素影响,发射箔条弹至舰艇与导弹中间一定位置,形成的箔条幕轴线方向与初始弹目方向基本垂直。三是舰艇机动,舰艇保持一定机动角度,同时保持稳定常速。
1.2 干扰场景模型构建
根据第1.1节中箔条幕干扰机理可构设干扰场景模型,以研究对象分类,具体包含导弹运动模型、舰艇运动模型和箔条幕模型。
1.2.1 模型假定与场景构设
为方便后续建模与计算,需做出如下定义:① 由于导弹跟踪目标过程中贴近海平面飞行,因此假定导弹、舰艇与海面处于同一二维平面内[10];② 以开始发现对方反舰导弹为初始时刻,定义坐标系为:初始时刻反舰导弹质心M所在正北方向为Y轴,垂直于Y轴且过舰艇质心S的轴所在正东方向为X轴正向,具体如图1所示;③ 定义反舰导弹运动过程中始终采取比例导引法[11-12];④ 定义舰艇为长度为2L的线段,且忽视其机动过程中为改变航向所做的回转运动所用的时间,S、Q和H时分别表示舰艇质心、舰艏和舰尾位置;⑤ 忽略箔条弹发射至完全散开所需时间;⑥ 定义箔条弹完全散开后呈一球状体。
空间场景:舰艇侦察到敌方反舰导弹,随即发射箔条弹,形成箔条幕干扰进行自卫;其中,初始时刻舰艇S与反舰导弹M的位置坐标分别为[Sx(0),Sy(0)]和[Mx(t),My(t)],弹目轴线MS与MO线的夹角为θ,发射箔条弹数量为n,相邻两枚箔条弹弹间距离为L1,幕墙轴线H2相较垂直轴线H1顺时针偏转α(α∈(-π/2,π/2)),幕墙质心C0与舰艇质心S的距离为L2,SC0与X轴正向的夹角为γ,干扰过程中风速为vf,风向角度为β。θ可表示如下:
θ=arctan(|Sx(0)/My(0)|)
(1)
1.2.2 导弹运动模型
t时刻导弹位置坐标如下所示:
(2)
式中:[Mx(t),My(t)]表示t时刻反舰导弹位置坐标;vm表示反舰导弹攻击速率;Bm(t)表示t时刻反舰导弹攻击方向与基准线夹角;Δt表示t-1时刻与t时刻的时间差值。
1.2.3 舰艇运动模型
t时刻,舰艇质心S的位置坐标为
(3)
舰艇首端Q的位置坐标为
(4)
舰艇尾端H的位置坐标为
(5)
式中:舰艇速率始终保持为vS;J0表示舰艇初始时刻行驶角度;ΔJ表示舰艇机动偏转角度。
1.2.4 箔条幕形态模型
根据实际布放经验,在单发箔条弹云团有效干扰时段内,其厚度完全能够满足电磁波的衰减要求,以有效发挥遮蔽作用,因此本研究从箔条幕轴线角度进行形态模型构建。
(1) 单发箔条弹形态
由王晴昊等[13-14]的分析可知,综合考虑互耦效应及箔条损坏因素,单发箔条弹完全散开后的平均有效反射面积σN为
(6)
由此可推得其平均有效反射半径R为
(7)
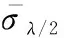
(2) 箔条幕形态
n发箔条弹构设的箔条幕轴线长度LC如下所示:
LC=(n-1)L1+2R
(8)
t时刻箔条幕质心坐标[C0x(t),C0y(t)]如下所示:
(9)
t时刻第i发箔条弹质心位置坐标[Cix(t),Ciy(t)]如下所示:
①若Sx(0)My(0)≥0,则
(10)
②若Sx(0)My(0)<0,则
(11)
t时刻箔条幕边缘点A和B的位置坐标([CAx(t),CAy(t)]、[CBx(t),CBy(t)])如下所示:
①若Sx(0)My(0)≥0,则
(12)
(13)
②若Sx(0)My(0)<0,则
(14)
(15)
1.3 求解模型构建
1.3.1 总体方法
箔条幕干扰构设过程中,在保证幕墙干扰作用正常发挥的基础上,即舰艇目标始终无法被反舰导弹有效跟踪且处于反舰导弹有效攻击范围之外[15-16],还需要同时考量箔条弹等作战资源的损耗程度,以保证战斗力的可持续性。显然,这两方面要素存在内在固有的矛盾,在实际布放中仅仅依靠人为主观判断难以得到科学的最佳平衡点。为此,在第1.2节干扰场景模型构建的基础上,采取仿生智能优化算法求取箔条幕布设方案,总体思路如图2所示。具体步骤如下:
步骤 1根据实际干扰情景,设置场景参数,包括反舰导弹与舰艇位置坐标、箔条云团有效半径、相邻箔条弹弹间距离、风向与风速等。
步骤 2设置约束条件与目标函数,约束条件即干扰成功的判断条件,目标函数为综合考虑干扰有效和资源消耗所设置的优化目标。
步骤 3定义参数变量,优化参数包含箔条弹数量n、舰艇机动角度ΔJ、箔条幕轴线偏转角度α、初始时刻箔条幕质心与舰艇距离L2及角度γ五维参量,根据实际场景设置每个优化参数的可优化范围。
步骤 4箔条弹补弹,当初始时刻反舰导弹与舰艇距离较大时,容易出现由于初始箔条幕持续扩散,最终无法有效衰减电磁波到指定程度从而暴露舰艇目标的现象,此时需要在箔条幕失效前进行补弹,并将相应补弹策略引入后续优化计算中。
步骤 5采取改进的灰狼算法对模型进行优化迭代,求取最佳布放方案。

图2 布放总体思路Fig.2 General idea of deployment
1.3.2 约束条件
约束条件具体包含遮蔽有效性约束条件、质心拖引有效性约束条件和干扰能力约束条件3类。
第1类为遮蔽有效性约束条件,即保证从初始时刻到反舰导弹起爆前,舰艇与导弹始终位于箔条幕轴线两侧,同时舰艇各点均位于箔条幕有效遮蔽范围内,具体如下所示:

(16)
(17)
式中:fC表示箔条幕墙轴线方程。将[Ux(t),Cy(t)](U=S,Q,H)、[Mx(t),My(t)]两点代入方程,当所得两个函数值乘积lUM小于0时,表示导弹与舰艇位置点U在箔条幕墙轴线两边,而当lSM、lQM和lHM均小于0时,表示舰艇整体均与导弹处于箔条幕轴线两侧;∠AMU和∠BMU表示箔条幕两边A和B分别与反舰导弹M和舰艇各点U形成的夹角,∠AMB表示A、M、B形成的夹角,zUA为∠AMU与∠AMB的差值,zUB为∠BMU与∠AMB的差值。当zUA、zUB均小于0时,定义zUC为-1,表示舰艇各点均被箔条幕有效遮蔽。
第2类为质心拖引有效性约束条件,即舰艇与幕墙质心的距离需始终大于反舰导弹有效杀伤半径,即下式中的tUC小于0:
(18)
式中:RM表示反舰导弹有效杀伤半径;LCU表示舰艇U(U=S,H,Q)点与箔条幕质心C0的距离。
第3类为干扰能力约束条件,如下所示:
LCiS-Rmax≤0,i=1,2,…,n,n≤nmax
(19)
式(19)表示所有箔条弹C1,C2,…,Cn所需发射距离LCiS均需要小于舰艇最大可发射距离Rmax,箔条弹损耗量n需小于储备量nmax。
1.3.3 目标函数
f表示目标函数,为干扰有效性与资源损耗性的耦合函数,如下所示:
minf=λ1fL+λ2fC+λ3fB
(20)
(21)
式中:fL表示箔条幕墙能量质心与舰艇质心的距离表征函数;fC表示箔条弹损耗表征函数;fB表示箔条弹发射损耗表征函数;λ1、λ2、λ3分别表示fL、fC和fB的权重系数,且有λ1+λ2+λ3=1。
1.3.4 箔条弹补弹策略
假设箔条幕持续有效作用时间为Tu,若反舰导弹起爆时刻Tb大于Tu,则需要进行补弹,详细补弹方法如下。
(1) 在每次箔条幕失效前Δt1时刻进行补弹,则所需要补弹的次数k和第q次补弹时刻Tq如下所示:
k=[Tb/(Tu-Δt1)]+1
(22)
Tq=q(Tu-Δt1),q=1,2,…,k
(23)
(2) 选取Tq时刻为新的初始时刻,为防止主动暴露目标,设定补弹后舰艇速度vS与机动角度(J0+ΔJ)均保持不变,选取此刻箔条幕所在轴线和能量质心为补弹初始时刻新的箔条幕轴线和能量质心,即α和[C0x(Tq),C0y(Tq)]保持不变,进而可得到补弹初始时刻箔条幕质心与舰艇距离L2及其角度γ为确定值。
(3) 根据Tq时刻空间场景设定基本参数,定义新的坐标系,将vS、(J0+ΔJ)、α、L2和γ定值参数输入改进的灰狼算法,随即进行优化迭代,输出第q次补弹方案。
1.3.5 改进的灰狼优化算法
灰狼优化(grey wolf optimizer, GWO)算法是一种模拟灰狼群体等级制度和狩猎行为的群体智能优化算法,于2014年由澳大利亚科学家Mirjalili等[17]提出,具有结构简单、鲁棒性强、参数设置简洁、全局寻优能力强等优点[18]。但随着应用场景的逐渐增多,该算法在处理维度较大、场景较为复杂的问题时,逐渐暴露出收敛速度较慢、易陷入局部最优等问题[19-20]。为更好地解决箔条幕干扰构设问题,本研究提出采取Logistic混沌映射和反向学习策略改进GWO算法,基本思路为将反向学习算法融入GWO算法的种群初始化过程,通过增强种群多样性和质量,提高摆脱局部最优的可能性,提高搜索速度。改进的GWO(improved GWO, IGWO)算法的详细优化步骤如下:
步骤 1参数设置,设置种群规模、搜索空间维数、最大迭代数等参数,基于GWO基本原理,收敛因子采用从2至0的线性收敛模式[21],向量系数A和C设置方式[22]分别如下所示:
A=2a·r1-a
(24)
C=2a·r2
(25)
式中:A和C为IGWO和GWO算法中的向量系数;r1和r2为[0,1]之间的随机数。
步骤 2种群初始化,采用Logistic混沌映射和反向学习策略生成N个初始种群[23-25]:
xiter1=μ·xiter1-1(1-xiter1-1)
(26)
(27)
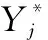
步骤 3适应度计算与位置更新,基于式(21)计算每个灰狼位置适应度值并排序,定义适应度最优的前3个灰狼个体位置为决策层;计算其他灰狼个体位置与决策层3个个体位置之间的距离,据此更新每个灰狼个体的位置。
步骤 4对当前种群中前m个灰狼个体位置进行更新。
步骤 5判断是否满足收敛条件,若满足,算法结束,否则进行下一次迭代。
2 仿真验证与作战效果评估
2.1 仿真案例
案例 1红方舰艇侦察发现蓝方反舰导弹雷达导引头开机,此时两者位置坐标分别为[25,0]km和[0,25]km,随即红方发射数枚箔条弹进行箔条幕自卫干扰。已知:反舰导弹飞行速度为300 m/s,初始视线角为0°,初始导弹速度向量角为0°,最大杀伤半径为100 m,雷达导引头工作频率为3 GHz;红方舰艇行驶速度为20节(10 m/s),初始行驶方向为30°,装载箔条弹总量为50,每颗箔条弹箔条数量为5×106根,相邻两枚箔条弹弹间距离L1为1.7R,单枚箔条弹云团最大可持续时间为50 s,每次补弹需提前3 s进行;舰艇可发射箔条弹最远距离为2 km;海风4级(风速为10 m/s),风向为-30°;为节省舰艇机动偏转使用时间,定义可机动范围为[-20°, 20°];λ1、λ2和λ3分别为0.4、0.3和0.3。
案例 2初始时刻,红方舰艇与蓝方反舰导弹的位置坐标分别为[10,0]km和[0,8]km,反舰导弹初始视线角为45°,初始导弹速度向量角为20°,舰艇行驶速度为10节(5 m/s),初始行驶方向为15°,可机动范围为[-180°,180°],风向为60°,风速为6 m/s,λ1、λ2和λ3分别为0.3、0.6和0.1,其余条件与案例1相同。
仿真实验均在 Inter(R) Core(TM) i7-1195G7 CPU @2.90 GHz、16 GB RAM、Ubuntu 22.04系统环境中运行。
2.2 方法有效性验证
以案例1为方法有效性仿真实验对象,采用IGWO、GWO、粒子群算法(particle swarm optimization,PSO)和正弦余弦算法(sine cosine algorithm,SCA)4种方法进行箔条幕布放方案求取[27-31],种群数量均设置为100,优化迭代次数均设置为100,搜索空间维数均设置为5,仿真结果如图3~图5和表1所示。

图3 算法优化迭代曲线Fig.3 Algorithm optimization iterative curves

图4 案例1箔条幕构设方案Fig.4 Construction scheme of chaff screen in Case 1

图5 案例1约束条件系数变化曲线Fig.5 Constraint coefficient variation curve of Case 1

表1 案例1箔条弹发射位置
由图3算法优化迭代曲线可知,4种算法中,采用IGWO算法寻优速率最快,仅迭代10次以内即可得到较优结果,且通过30次仿真实验统计可知,采用IGWO算法的平均计算时间为0.993 2 s,布放方案构设时间在可接受范围内。
图4为针对案例1求取的箔条幕布放方案。仿真计算结果表明,案例1自卫场景下最佳优化参数分别为:箔条弹数量n为10、舰艇机动角度ΔJ为20°、箔条幕轴线偏转角度α为4.48°、初始时刻箔条幕质心与舰艇距离L2及其角度γ分别为261.1 m和80.34°;整个自卫干扰过程共持续113.7 s,需进行3次箔条弹布放,包含一次初始时刻布放和2次补弹;初始时刻需发射箔条弹6枚,发射位置如图4和表1中箔条弹1号~6号,最远发射距离为6号箔条弹对应的525.4 m,满足最大发射距离要求;两次补弹均需发射箔条弹2枚(分别对应箔条弹7号、8号和9号、10号),补弹时刻分别为47 s和94 s,最远发射距离分别为625.3 m和1 153.4 m。而针对案例1,常规箔条幕布设方法[7]共需布放24枚箔条弹,包括一次初始布放,两次补弹,每次布放箔条弹数量均为8。图5为遮蔽有效性约束条件系数、质心拖引有效性约束条件系数变化曲线,在整个对抗过程中各系数数值始终小于0,而箔条弹数量限制和发射距离限制均已在参数生成过程中完成约束,因此结果满足干扰能力约束条件,同时最终反舰导弹引爆时刻距离舰艇最近距离为1 355.5 m,大于导弹杀伤半径,由此证明在整个对抗过程中箔条弹自卫干扰效果始终有效。
综上分析,本研究提出的箔条幕布放策略能够满足海战场环境下有效干扰反舰导弹雷达导引头跟踪且保护舰艇的要求,且相对常规箔条幕布放方法有效减少了箔条弹消耗量。
2.3 作战效果影响因素分析
以案例2作为作战效果影响因素分析的仿真对象,在求取基本布放方案的基础上,分别从风速与风向、初始弹目距离以及舰艇机动4个因素对最终自卫干扰效果影响程度进行分析,算法参数设置与案例1一致。
2.3.1 案例2布放方案分析
通过仿真计算求得案例2场景下最佳优化参数分别为:箔条弹数量n为2,舰艇机动角度ΔJ为-14.55°,箔条幕轴线偏转角度α为-1.31°,初始时刻箔条幕质心与舰艇距离L2及其角度γ分别为533.4 m和148.99°。在案例2对抗场景下,舰艇仅需进行一次初始布放,无需补弹,具体见图6布放方案中的箔条弹1号和2号,初始时刻所需箔条弹发射距离分别为543.1 m和530.2 m,反舰导弹引爆位置与引爆时刻舰艇位置距离为488.6 m,满足自卫要求,整个自卫干扰过程持续41.2 s。

图6 案例2箔条幕布放方案Fig.6 Construction scheme of chaff screen in Case 2
2.3.2 箔条幕构设方向分析

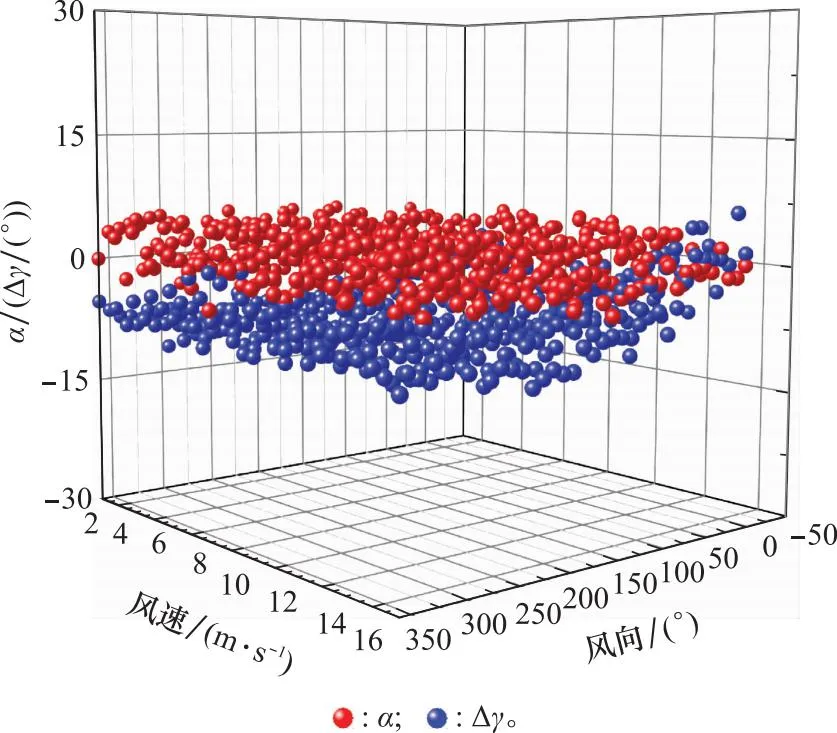
图7 不同风速风向箔条幕方向特征值Fig.7 Characteristic coefficients of the chaff screen direction at different wind speeds and directions

图8 不同攻击距离与攻击角度箔条幕方向特征值Fig.8 Characteristic coefficients of the chaff screen direction at different attack distances and different attack angles

表2 箔条幕方向特征值期望值与标准差
2.3.3 风速与风向影响分析
设置1 m和10°分别为风速与风向单位增量,仿真分析1~15 m风速条件和0°~360°风向条件下箔条幕布放方案,其余条件与案例2一致,仿真结果如图9和图10所示。其中,图9为目标函数值图,图10为箔条弹使用量图。由图9可知,优化求取的目标函数值均小于1,而图10显示所需箔条弹数量均为2或3,且均只需进行一次布设;进一步分析求取的最优参数与风向及风速的关系,并未发现明显的规律性变化关系,由此可见在不同风速与风向条件下均可求得有效的箔条幕布设方案,且其对最终布设结果影响较为有限。

图9 不同风速与风向目标函数值Fig.9 Objective function values of different wind speeds and different wind directions

图10 不同风速与风向箔条弹使用量Fig.10 Usage of chaff screen for different wind speeds and different wind directions
2.3.4 初始弹目距离与攻击方向影响分析
定义反舰导弹朝向舰艇艏向攻击为攻击角度(0°),沿顺时针旋转攻击角度逐渐增大,设置20°和2 km分别为攻击角度和初始弹目距离单位增量,仿真分析0°~340°攻击角度和2~32 km初始弹目距离条件下箔条幕布放方案,其余条件与案例2一致,仿真结果如图11和图12所示。由图11目标函数值计算结果可知,本仿真计算的目标函数值均小于1,证明研究在不同场景下均可得到有效的箔条弹布放方案。综合图11和图12箔条弹用量分析结果可知:① 以初始弹目距离为基本变量,目标函数值无明显规律性变化,但其对箔条弹用量及是否需要补弹影响较大。在2~14 km范围内,只需进行一次箔条弹布放,箔条弹用量为2~3;在16~28 km范围内,需进行一次补弹,箔条弹用量为3~5;在30~32 km范围,需进行两次补弹,箔条弹用量为6~8;② 以攻击角度为基本变量,分析得出攻击角度越接近180°,即反舰导弹从舰艇尾向进行攻击时,目标函数值越小,最小值为0.059,证明自卫干扰综合效果越好。当攻击角度越接近0°,即反舰导弹从舰艇艏向进行攻击时,目标函数值越大,最大值为0.176,自卫干扰效果相对越差。综上所述,初始弹目距离主要影响箔条弹用量,而反舰导弹攻击方向对自卫干扰综合效果影响较为明显。

图11 不同初始弹目距离与攻击角度下的目标函数值Fig.11 Objective function values for different initial missile distances and different attack angles

图12 不同弹目距离与攻击角度下的箔条弹用量Fig.12 Usage of chaff screen for different initial missile distances and different attack angles
3 结 论
针对海战场环境中舰艇采取箔条幕方式干扰反舰导弹雷达导引头跟踪问题,提出了一种采用IGWO算法进行箔条幕干扰构设的方法。在对箔条幕干扰机理进行分析的基础上,构建了干扰场景模型和布放方案求解模型;其中,干扰场景模型具体包含导弹运动模型、舰船运动模型和箔条幕形态模型;干扰方案求解模型则基于采用灰狼算法进行布放方案求取的总体思路,构建了遮蔽有效性约束条件、质心拖引有效性约束条件和干扰能力约束条件3类约束条件,综合考虑干扰有效性与资源损耗性,构设了目标函数,建立了补弹策略,采用Logistic混沌映射和反向学习策略改进了灰狼优化算法。最终通过仿真案例分析得出,本研究提出的箔条幕构设方法寻优速率较快,可保证整个对抗过程中舰艇始终能够有效自卫干扰;初始时刻构设的箔条幕轴线基本与弹目轴垂直,而箔条幕质心基本处于弹目轴线附近;风速风向对箔条幕干扰效果影响较小,初始弹目距离主要影响箔条弹用量,而反舰导弹攻击方向对自卫干扰综合效果影响较为明显,当从舰艇尾向进行攻击时,干扰效果最好,相反从艏向进行攻击时,干扰效果最差。

