一种基于稀疏重构的多视角MIMO雷达关联成像算法研究

张 弓, 田雨薇, 袁家雯, 张 宇

(1. 南京航空航天大学电子信息工程学院, 江苏 南京 210016; 2. 南京工程学院信息与通信学院,江苏 南京 211167; 3. 南京信息工程大学电子与信息工程学院, 江苏 南京 210044)

0 引 言

雷达成像技术拓宽了早期雷达测速和测距的功能,具有全天时、全天候观测,以及受天气影响小的工作特点,因此得到了迅速的发展,被广泛应用于军事预警、电子对抗和遥感测绘、抗震救灾等领域[1-3]。雷达成像技术按照雷达与目标是否存在相对运动可分为相对运动雷达成像和相对静止雷达成像。相对运动雷达成像主要包括合成孔径雷达(synthetic aperture radar, SAR)成像[4]和逆SAR(inverse SAR, ISAR)成像[5]。通过相对运动,可合成更大的虚拟合成孔径,扩大观测视角,提高方位向分辨率,但当相对转角小、目标观测条件不理想时,分辨率会受到影响,成像效果差。相对静止雷达成像主要指实孔径雷达[6],通过波束扫描实现对重点区域的连续观测,其成像方位向分辨率受制于天线阵列孔径的大小。

雷达关联成像是借鉴光学“鬼成像”[7-8]提出的一种全新体制的相对静止成像雷达,通过多个独立的辐射源发射随机调制信号,在成像区域形成一个时空随机辐射场。通过回波与推演得到的参考信号辐射场的关联处理即可实现高分辨率成像。雷达关联成像不依赖于目标与雷达间的相对运动,可以突破传统雷达成像中天线孔径对分辨率的限制,实现短时间内对固定区域的连续高分辨成像。作为一种新体制的高分辨率雷达成像方式,近十余年来,雷达关联成像受到了国内外的广泛关注。众多学者从成像机理与分辨率表征[9-10]、随机辐射场构造[11-12]、重构算法[13-14]以及失配修正[15-16]等方面相继开展了对雷达关联成像的研究,促进了雷达关联成像的发展。

重构算法是雷达关联成像的研究重点。现有的关联成像重构算法主要分为相关法和参数重构法。相关法是最基本的关联成像算法,对噪声和模型误差的鲁棒性高,但分辨率受制于阵列孔径,无法实现超分辨成像。参数重构法又包括伪逆法(最小二乘法)[17]、正则化法[18-19]和稀疏重构法[13]等。最小二乘法可突破瑞利限,实现超分辨成像,但对模型误差和噪声敏感。在实际成像过程中,由于发射信号不理想、收发阵列布局、成像单元的划分等因素的影响,参考矩阵并不完全正交,呈现出病态性。为了降低参考矩阵病态性对成像的影响,有学者[20]将正则化策略引入了雷达关联成像,提出了Tikhonove正则化方法、截断奇异值分解(truncated singular value decomposition, TSVD)方法和全变差正则化方法,其中全变差正则化方法在保持逆问题求解性的同时,可保持边缘的细节特性,但相比其他两种正则化方法,该算法对噪声更敏感。经典的稀疏重构算法,例如光滑l0范数算法[21]、基追踪算法[22]、正交匹配追踪算法[23]、稀疏贝叶斯学习[24-26]等算法,已被应用于雷达关联成像中,并获得了较高的成像质量。

雷达关联成像依靠辐射场的时空随机性进行成像。现有的雷达关联成像研究都是多输入单输出(multiple input single output, MISO)关联成像,通过对发射信号与发射阵型的设计可提高辐射场信号的随机性,突破传统雷达成像中天线孔径对分辨率的限制进而实现超分辨成像。多输入多输出(multiple input multiple output, MIMO)雷达采用多个发射天线和接收天线,通过发射天线的波形设计以及收发阵列的协同工作,增加了雷达系统的自由度,具有良好的探测性能[27]。有学者研究多点接收的雷达关联成像机理,将多个接收通道的数据联合处理,不仅加快样本获取,而且降低参考矩阵的病态性,可有效改善成像质量[28-29]。采用MIMO雷达关联成像,通过空间维的扩展及多个接收通道的数据联合处理,可提高辐射场信号的随机性,从而突破MISO雷达关联成像的分辨率极限,实现超分辨成像。

雷达散射面积(radar cross section, RCS)起伏特性是雷达目标的基本属性。SAR成像技术通过目标与雷达之间的相对运动形成大转角,等效扩大了雷达天线孔径,也有利于对目标形成多视角观测。MISO关联成像通过多个发射阵元协同工作,可对目标形成多视角观测,而在以往雷达成像研究中往往将目标建模为各向同性的理想点目标。MIMO雷达关联成像通过增加接收通道,可进一步扩展观测视角。本文在扩展视角的同时,建立复杂目标RCS起伏模型,有助于更全面地表现复杂目标。但多视角目标RCS起伏特性使关联成像模型中接收回波与参考信号的相关性退化,严重影响成像质量。

针对多视角MIMO雷达关联成像中复杂目标RCS起伏的相关性退化问题,本文分析了复杂目标多视角RCS起伏,建立了多视角MIMO雷达关联成像模型,提出了一种基于稀疏重构的多视角MIMO雷达关联成像算法,将目标的稀疏性作为先验条件,约束目标RCS起伏能量,来自适应更新目标RCS值,解决多视角RCS起伏下回波与参考矩阵相关性退化问题。同时,通过全变差正则化项最小化,可实现相邻成像单元间的平滑,提高成像的主观视觉效果。

本文所提出的复杂目标MIMO雷达关联成像算法具有如下优势:

(1) 通过对多接收通道数据的联合处理以及目标RCS起伏能量的约束,实现成像单元多视角RCS均值的精确获取,可全面反映目标特性,有效改善RCS起伏下关联成像的质量;

(2) 与多个接收通道各自MISO关联成像求解后进行平均操作所得的成像结果相比,MIMO雷达关联成像通过扩展空间维,提高了辐射场参考信号的随机性,且一次稀疏重构成像、关联成像分辨率更高;

(3) 在本文所设计的稀疏重构模型中引入全变差正则化最小化项,可实现相邻成像单元间平滑,同时又可保留成像结果的不连续边界,增强雷达关联成像图像的整体表现。

1 信号模型

MIMO雷达关联成像原理图如图1所示。假设雷达阵列含有M个发射天线,N个接收天线。由于成像单元不能无限划分,将成像平面离散为L个大小相同的成像单元,假设目标散射点中心位于成像单元中心。Rm和Rn分别表示第m个发射阵元和第n个接收阵元的位置矢量,rl为成像场景中第l个成像单元中心的位置矢量,c为光速。用Sm(t)表示相互正交的发射信号,第n个接收通道下的第l个成像单元对应的辐射场参考信号An(rl,t)可表示为

(1)

图1 MIMO雷达关联成像原理图Fig.1 MIMO radar coincidence imaging’s principle schematic

一般地,考虑到实际目标的散射特性必然随观测视角变化,雷达关联成像都采用理想点目标。为简化多视角关联成像模型,本文将发射多视角下的目标RCS值做平均化等效,增加接收通道多视角,仅考虑接收通道视角变化对目标RCS的影响,那么第n个接收通道的回波信号yn(t)可表示为

(2)

式中:wn(t)为第n个接收通道的噪声;σn,l为第n个接收视角下第l个成像单元中心所对应的散射系数。此时,各接收通道所反映的目标RCS是变化的。

可根据式(2)中的回波表达式,对时间离散化,时间采样数为J,构造第n个接收通道所对应的雷达关联成像方程:

yn=Anσn+wn

[wn(t1),…,wn(tJ)]T

(3)

式中:yn为第n个接收通道的回波向量;An为推演得到的第n个接收通道的参考矩阵;σn为第n个接收通道的散射系数向量;wn为第n个接收通道的噪声向量。

在实际中,目标RCS起伏是随机的、不规律的。目前,往往用统计学的方法对目标RCS起伏定量表征,现有的RCS起伏模型主要包括经典起伏模型和现代起伏模型。前者主要包括马克姆模型和Sweling1～4模型,后者有卡方分布模型、对数正态分布模型、赖斯模型等。由于对数正态分布模型的平均中值比ρ为可变参数,可拟合多种类型的目标,基本涵盖了大多数现代雷达目标RCS的起伏规律[30],因此本文采用这种模型。对数正态分布模型目标RCS的随机变量σ的概率密度函数表达式如下:

σ>0

(4)

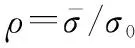
采用MIMO体制,得到了N个接收通道的回波数据,可用数据层扩维融合方法,将多接收通道的回波数据在时间维进行拼接,通过扩展空间维提高辐射场参考信号的随机性,推导出基于多视角RCS起伏的扩维成像方程:

(5)

2 基于稀疏重构的多视角MIMO雷达关联成像算法

2.1 成像模型

在MIMO雷达多视角关联成像场景中,存在目标多视角RCS起伏,为保证多视角RCS起伏下的关联成像质量,得到全面反映各视角RCS起伏特性的多视角综合图像,期望MIMO雷达多视角关联成像的结果表现为成像单元多视角RCS起伏平均。

关联成像重构是一个经典的线性逆问题,全变差正则化算法在保持逆问题求解稳定性的同时,具有良好的边缘保持特性,在图像复原和去噪领域得到了广泛的认可和应用。近年来,也有学者将全变差正则化算法应用于雷达关联成像,在有噪情况下得到稳健的高分辨成像结果[18]。全变差正则化表示的是空间梯度的范数,表达式为

(6)

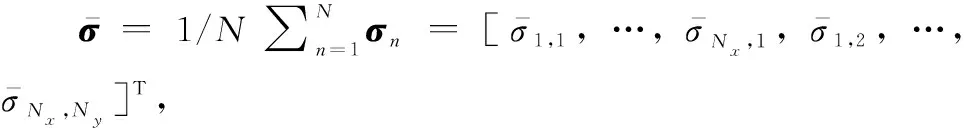
(7)

多视角稀疏关联成像模型建立的主要思路如下:针对稀疏成像场景,可以将目标的稀疏性作为先验条件引入多视角关联成像的成像模型中,并对RCS起伏能量进行约束。为进一步改善图像质量,保留目标边缘细节特征,在目标函数中增加全变差正则化项。在多视角RCS起伏下,雷达关联成像模型可表示为

(8)

将目标RCS的稀疏项和全变差正则化项作为目标函数,可在对目标重构的同时,实现空间平滑。同时,式(8)中对RCS起伏能量的约束项可以削弱多视角RCS起伏对参考矩阵与回波之间相关性的影响,实现成像单元多视角RCS均值的精确获取,全面反映目标特性。综上所述,本文所提方法不需要计算各个视角的RCS值,即可一次重构得到包含多视角RCS信息的高分辨图像。

2.2 基于稀疏特性的全变差正则化算法求解

(9)

使用Lagrange乘子将约束函数写入目标函数,可以得到:

(10)

式中:(·)*表示矩阵的共轭转置。该目标函数取得极值的条件如下:

(11)

(12)

(13)

对式(11)进行推导,(·)†表示对矩阵求伪逆,可得

(14)

(15)

(16)

将式(12)代入式(16),可得出Lagrange乘子的更新计算公式,即

(17)

(18)

(19)

基于不动点迭代法的全变差正则化信息处理迭代公式如下所示:

(20)

其中,迭代步长为v(l)=-(H(l))-1G(l)。

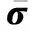
算法 1 基于稀疏重构的多视角算法输入 A,y初始化:σ-(0)=0,λ(0)=1循环:1) 由式(13)计算L(l)=L(σ-(l));2) 根据式(18)计算目标函数的梯度:G(l)=μL(l)σ-(l)+λ(l)A*·(Aσ-(l)-y)+Λ(l)σ-(l);3) 根据式(19)计算目标函数的近似Hessian矩阵:H(l)=L(l)+λ(l)A*A+Λ(l);4) 采用不动点迭代法,计算迭代步长v(l),满足方程;5) 更新全变差迭代结果:σ-(l+1)=σ-(l)+v(l);6) 根据式(17)更新参数λ(l+1);7) 令l=l+1,直到到达最大迭代次数lmax。输出 ^σ=σ-(lmax)

3 仿真结果

为验证本文所提出的算法,采用多发多收天线阵列,发射和接收阵列均采用均匀线阵,仿真的参数设置如表1所示,其中发射信号为一组相互独立的噪声调幅信号。天线阵列与成像场景位于同一个平面,阵列与成像场景之间的距离d=100 m。成像单元大小为0.24 m,成像目标均位于成像单元中心,目标RCS随接收视角变化而起伏,随视角变化满足对数正态分布。

表1 关联成像参数设置

下面分别采用伪逆算法[17]、TSVD法[31]、全变差正则化算法[20]、迭代收缩算法[32]、正交匹配跟踪(orthogonal matching pursuit, OMP)算法[23]以及本文所提出的基于稀疏重构的多视角MIMO雷达关联成像算法进行仿真和对比。仿真图呈现的是15×15个成像单元,成像单元的RCS值由对应单元的颜色表示,颜色越亮,表示该成像单元的RCS值越大。考虑噪声在实际场景中的影响,在实验中设置信噪比为10 dB。图2给出了目标RCS起伏在接收端满足均值为15 dBsm、方差为10 dBsm的对数正态分布时,100次蒙特卡罗实验的成像结果,图2(a)～图2(i)为9个接收视角下的目标场景,可表现同一成像单元的目标在不同视角下的RCS起伏特性,而图2(j)表示多视角RCS取平均的综合目标场景。由图3可知,在存在方差为10 dBsm的RCS起伏情况下,各种算法均可实现目标的反演成像,但伪逆算法、TSVD法和全变差正则化算法下部分背景区域的散射系数值高,部分区域目标无法清晰分辨。而迭代收缩算法、OMP算法和本文所提算法利用了目标的稀疏先验信息,具有良好的求解能力,重构的目标轮廓清晰可识别。通过计算可得伪逆算法、TSVD法和全变差正则化算法的NMSE依次为4.2 dB、-20.1 dB和-4.1 dB,而迭代收缩算法、OMP算法的NMSE分别为-63.2 dB和-66.48 dB,本文所提算法的NMSE为-68.3 dB,可进一步说明迭代收缩算法、OMP算法和本文所提算法在RCS起伏小时,成像效果好,并且本文所提算法的成像效果最好。

图2 多视角RCS起伏方差为10 dBsm时的成像场景图Fig.2 Image scene diagram of fluctuation variance with multi-view RCS of 10 dBsm

图3 RCS起伏方差为10 dBsm时不同算法的成像结果图Fig.3 Imaging results diagram of different algorithms with fluctuation variance of RCS of 10 dBsm

图4为RCS起伏增大、在接收端满足均值为15 dBsm、方差为50 dBsm的对数正态分布时,100次蒙特卡罗实验的成像场景图。图5成像结果显示,由于多视角RCS起伏特性导致参考矩阵与回波之间相关性严重失配,伪逆算法和全变差正则化算法已经完全失效,TSVD法、OMP算法和迭代收缩算法也出现了不同程度的成像模糊,成像目标与背景之间不能很好地区分,部分区域目标已无法分辨。本文所提算法可在一定程度上削弱多视角RCS起伏的影响,重构的图像依旧可以清晰地分辨出目标,背景区域散射系数值低,进一步说明了基于稀疏特性的全变差正则化算法的稳健性。

图4 多视角RCS起伏方差为50 dBsm时的成像场景图Fig.4 Image scene diagram of the fluctuation variance with the multi-view RCS of 50 dBsm

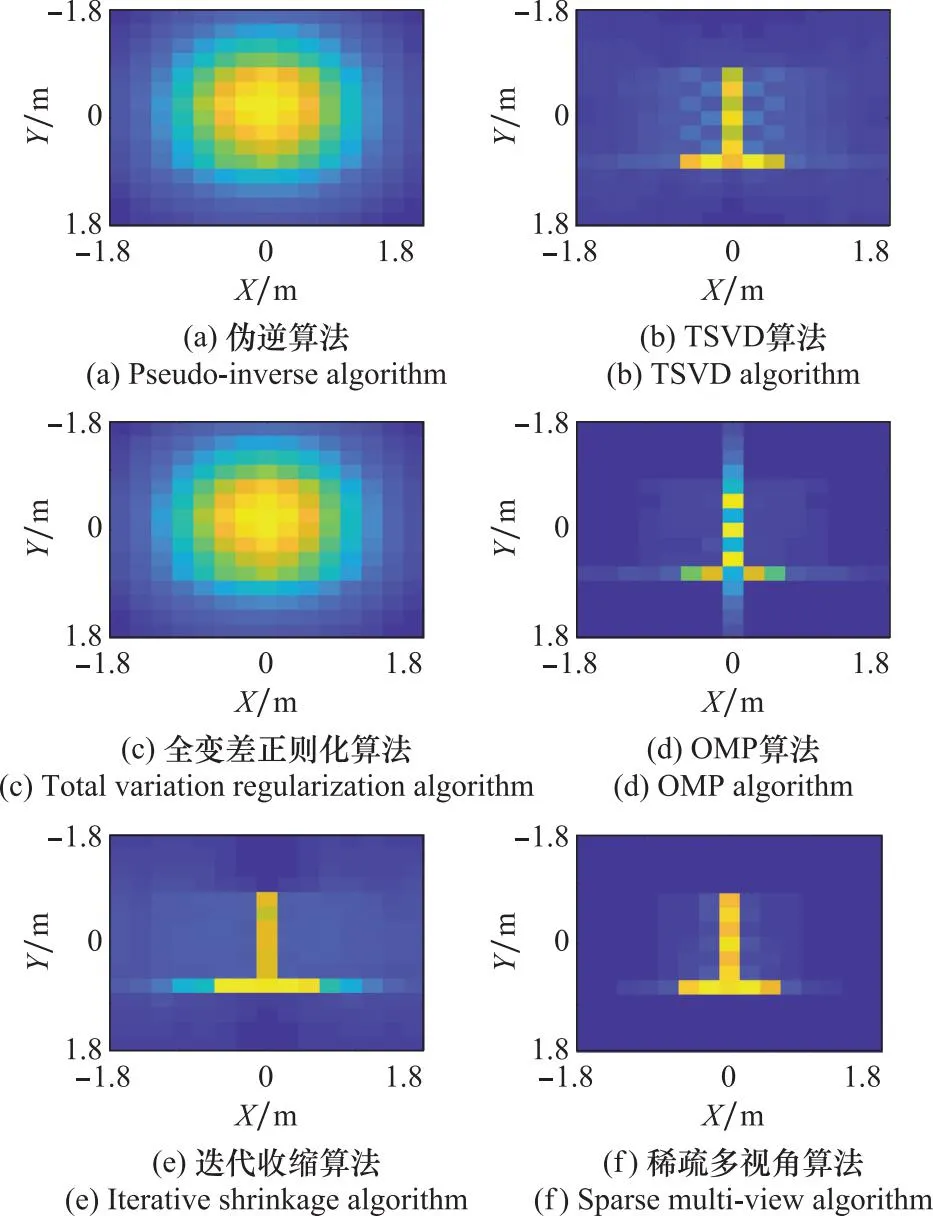
图5 RCS起伏方差为50 dBsm时不同算法的成像结果图Fig.5 Imaging results diagram of different algorithms with fluctuation variance of RCS of 50 dBsm

图6为目标RCS起伏在接收端满足均值为15 dBsm、方差为30 dBsm的对数正态分布时各算法在不同时间采样数下的NMSE。随着时间采样数的增加,各算法的NMSE均呈减小趋势。基于稀疏重构的多视角MIMO雷达关联成像算法的NMSE在不同时间采样数下都是最小的,且NMSE随时间采样数的变化小,在时间采样数较少时,依旧具有良好的成像效果。

图6 不同时间采样数下各算法的NMSE比较Fig.6 NMSE comparison of different algorithms with different time sampling numbers

图7显示了不同算法在RCS起伏方差从-10 dBsm到70 dBsm下的NMSE。可以看出,所有算法都随着RCS起伏方差的增大而出现成像质量恶化的趋势,稀疏重构算法的效果优于伪逆算法和全变差正则化算法,而稀疏多视角算法效果最好,该算法在RCS起伏较大时,NMSE依旧较小,说明了该算法在多视角观测方面的优越性。

图7 不同RCS起伏下各算法的NMSE比较Fig.7 NMSE comparison of different algorithms with different RCS fluctuations

4 结束语

为了实现多视角下的MIMO雷达关联成像,本文分析了目标RCS起伏对MIMO雷达关联成像的影响机理,建立了RCS起伏下的成像模型,并提出了基于稀疏重构的多视角MIMO雷达关联成像算法。在利用MIMO体制扩充探测视角的同时,增加了数据维度,提高了辐射场信号随机性,为进一步提高成像分辨率提供了条件。该算法建立了多视角下的稀疏重构模型并结合全变差正则化项,改善了多视角RCS起伏造成的接收回波与参考信号的相关性退化对关联成像质量的影响问题。与MISO雷达关联成像相比,MIMO雷达关联成像分辨率更高、成像整体表现更好。目前,已完成了该体制雷达仿真研究,验证了所提算法的有效性,后续将进行实验验证,同时算法效率提升也有待进一步研究。