基于FAST和Sobol指数法的雷达系统效能敏感性分析

胡 涛, 申立群, 朱镜达, 孙成会, 董伟锋

(哈尔滨工业大学仪器科学与工程学院, 黑龙江 哈尔滨 150001)

0 引 言

现代化战争以信息战为基本形态,集海洋、陆地、天空、太空、网络五位于一体[1-2],雷达作为战争信息化的重要标志,具有远距离探测、空中指挥等功能,是决定战争胜负的关键节点。但对空探测雷达研制经费高昂、研制周期较长,在现有条件下研究如何以较小代价快速提升雷达系统的综合效能已成为一大难题。

近年来,国内学术界对雷达的效能分析开展了广泛研究。文献[3]构建了舰机综合雷达对抗侦察模型,从侦察范围、侦察数据更新率等方面分析了舰机综合雷达对抗侦察效能。文献[4]分析构建了相控阵雷达信息保障的层次结构,利用层次分析法对雷达信息保障效能进行了定量的评估。文献[5]针对目标指示雷达的配置优化问题,建立了雷达情报保障综合效能评估模型,并应用典型参数验证了该评估模型的有效性。以上研究只是定量计算出雷达效能的大小,并没有找出影响雷达效能的性能指标,而且大多数也只考虑了雷达本身某方面的能力,并没有从雷达全系统的角度出发进行综合效能分析。同时,目前对对空探测雷达的综合效能分析较少,极少延伸到系统的性能指标层面,无法为对空探测雷达综合效能的提升提供更具有指导意义的结论。鉴于以上问题和不足,本文在建立对空探测雷达综合效能评估模型的基础上,采用敏感性分析的方法力求找到影响对空探测雷达综合效能的性能指标。

敏感性分析主要用来研究各输入因子发生一定变化时,模型输出发生的变动大小[6-7]。敏感性分析方法的归类并不唯一[8-10],最常见且最受认可的是将其分为局部类型和全局类型的敏感性分析方法。全局敏感性分析方法目前在经济[11-12]、工程[13-14]和生态[15-16]等领域都有广泛的应用,主要包括傅里叶幅度敏感性测试(Fourier amplitudes sensitivity test, FAST)和Sobol指数法。文献[17]运用改进的FAST方法分析了各参数对陆面过程模式输出的影响,推进了陆面过程模式参数化方案的优化。文献[18]使用Sobol指数法对装备体系可用度进行敏感性分析,得到装备体系保障能力指标的重要程度,定量衡量了装备体系保障的效果。但有研究表明[19-20],由于采用的敏感性分析方法不同,分析结果也会有些许差异。因此,本文为了使分析结果更加准确可靠,用FAST和Sobol指数法来对对空探测雷达系统综合效能分别进行频域和时域的敏感性分析,并将分析结果进行对比验证,为综合效能的提升提供可靠的依据。

综上所述,本文为了研究如何能以较小的代价快速提升对空探测雷达系统的综合效能,利用FAST和Sobol指数法来对对空探测雷达系统综合效能分别进行频域和时域的敏感性分析,找到影响综合效能的主要参数指标。本文首先搭建了对空探测雷达系统综合效能的评估指标体系,在此基础上建立了综合效能评估模型。为了得到更加准确可靠的分析结果,使用FAST和Sobol指数法这两种全局敏感性算法对模型进行分析,得出了各参数指标对对空探测雷达系统综合效能的敏感性大小。最后,对比两种分析方法得到的敏感性分析结果,找到综合效能的主要影响指标,为后续对空探测雷达的研发和改进提供依据。

1 对空探测雷达系统评估模型建立

1.1 指标体系的建立

根据对对空探测雷达主要任务场景的分析,并参考文献[21-23]中的相关研究,构建了评估模型的指标体系结构,如图1所示。本文将对空探测雷达系统综合效能评估体系结构分为效能层、能力层和指标层,并对指标层的各个指标采用参数公式、直接定量、专家打分的方式进行评价,最终形成了影响雷达系统综合效能的参数层。

图1 对空探测雷达系统指标体系整体结构Fig.1 Overall structure of index system of air detection radar system

采用参数公式进行评价的指标主要有最大作用距离、测距测角精度以及系统可靠性等,这些二级指标与对空探测雷达参数之间存在确定的公式对应关系[24]。

(1) 最大作用距离Rmax表征的是对空探测雷达能收集到的目标信息的最远距离,考虑实际评价需要,作用距离方程可使用如下形式:

(1)

式中:Pav为发射机平均功率;Ar为接收天线的有效孔径面积;Tr为信号重复周期;Ls为系统损耗;S/N为信噪比;kl为雷达衰减系数。

(2) 距离测量精度σΔR与对空探测雷达信号带宽B以及信噪比有关,且满足如下关系式:

(2)

式中:c为光速,取值为3×108m/s。

(3) 对空探测雷达每一次测量在方位和仰角上的误差可分别表示为

(3)

式中:Δφ1/2为天线波束在方位上的半功率点宽度;Δθ1/2为天线波束在仰角上的半功率点宽度;Km为单脉冲测角时角灵敏度函数的斜率(误差斜率)。

(4) 对空探测雷达通常采用测量多普勒频率的方式来获取目标径向速度,使用该测速方式达到的测量精度如下:

(4)

式中:λ为工作波长;Td为相干积累时间,σΔv为多普勒滤波器的带宽,受波束驻留时间等条件限制,一般为10 ms。

(5) 对空探测雷达系统的可靠性可用两个参数来描述,通过以下关系式可将系统可靠性扩展到参数层:

(5)

式中:MTBF(mean time between failure, MTBF)为平均故障间隔时间;MTTR(mean time to repair, MTTR)为平均修复时间。

采用直接定量的方式进行评价的指标主要包括方位角和俯仰角的观察范围等,这些指标本身可用一定的数值来量化表示。例如,方位观察范围Ra一般指对空探测雷达在方位上能够观察到的范围,目前对上装载雷达的方位检测能力要求较高,为全方向覆盖,即Ra为360°;俯仰观察范围Rp为对空探测雷达在俯仰角上能够检测到的范围,在保证能完成观测任务的情况下,天线俯仰观察范围扩展到±30°即可满足要求。

采用专家打分的方式进行评价的指标主要有环境适应性和抗毁伤性等,这些指标通常是以定性的方式进行分析,本文采用专家打分的方式对定性指标进行量化。例如,环境适应性是指对空探测雷达对恶劣环境的适应性[25],环境适应能力越强,使用局限性越小,适用条件更加广泛;抗毁伤性是指对空探测雷达能够承受外部攻击并保持正常工作的能力[26],抗毁伤性越强,承受外界攻击的能力就越强。以AN/APY-1型号雷达为例,对此雷达的环境适应性和抗毁伤性采用专家打分的方式进行量化,打分分别为80分和85分。

1.2 指标权重的确定

根据搭建的对空探测雷达系统综合效能评估指标体系,为了保证指标权重的客观性,本文基于德尔菲(Delphi)专家咨询法[27]进行打分来确定指标权重。邀请专家组根据各个指标在评估体系中的重要程度进行打分,运用层次分析法来计算系统各项指标相对上一层指标的权重。指标权重汇总如表1所示,各指标按权值累加后,可建立起对空探测雷达系统的综合效能评估模型。

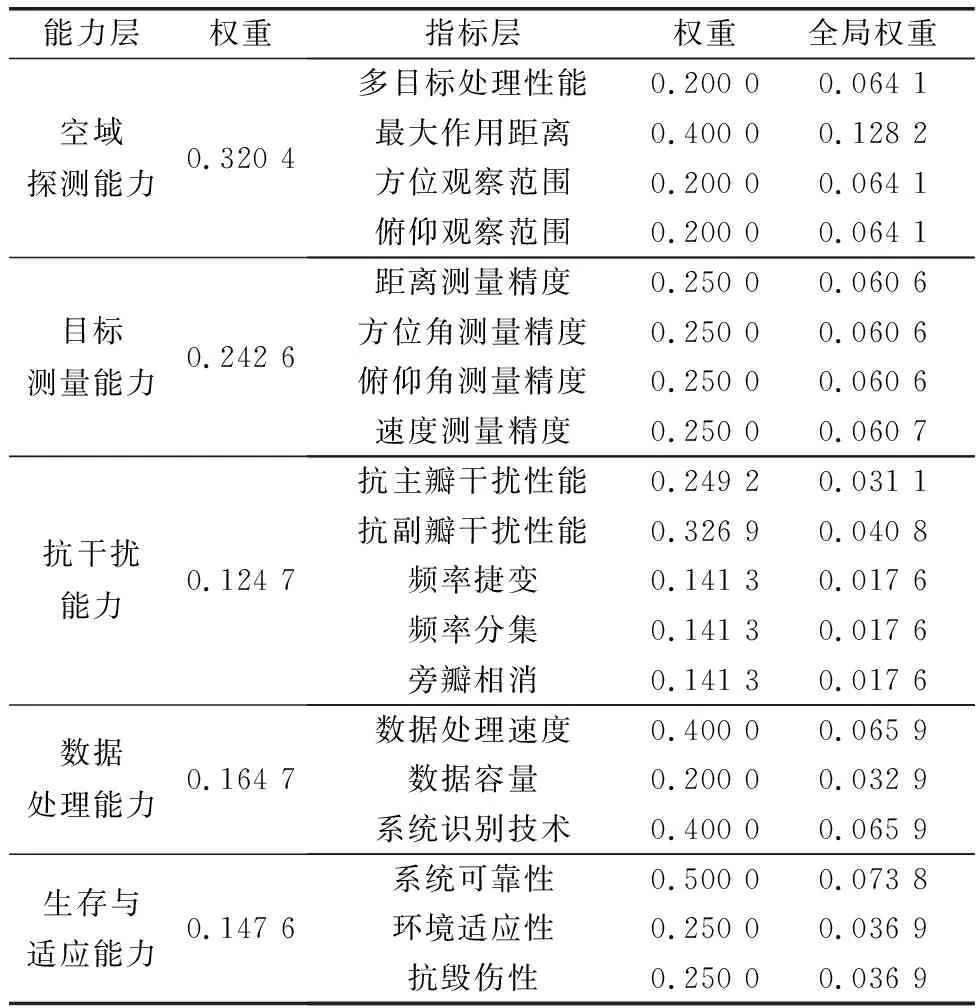
表1 指标权重汇总

如表1所示,得到一级和二级指标的权重后,可通过计算得到二级指标层相对顶层综合效能的权重,称为全局权重。

1.3 参数取值处理与评估模型建立

1.3.1 数据的归一化处理

为使不同属性、不同数量级、不同量纲的参数层的各个变量值能够共同表述对空探测雷达系统的综合效能值,应将参数的取值作相应的归一化处理,使得参数变量的取值区间变为[0,1]。效用函数是以函数映射的方式对不同类型的指标值进行归一化处理,适用性广、操作灵活,常用的函数形式有线性、折线、二次曲线等。考虑到文中涉及的二级指标均为效益性指标或成本型指标,为进一步简化归一化过程,本文采用线性效用函数完成对参数层的各个变量值的归一化,线性函数的一般形式如下:

(6)

式中:(x0,y0)和(x1,y1)为根据指标取值范围及指标所属类型配置的效用点。效用点的取值和指标值的类型有关,如表2所示。

表2 效用点取值

以多目标处理性能和测量距离精度为例,若多目标处理性能的不满意值设定为0,满意值设定为800,当多目标处理性能的指标值为600时,对应效能值为0.75,多目标处理性能的指标值越大,效能值越高,此为效益型指标特征。若距离测量精度的不满意值设定为200 m,满意值设定为0 m,当距离测量精度的指标值为20 m时,对应效能值为0.9,距离测量精度的指标值越小,效能值越高,此为成本型指标特征。根据指标值的不同类型和不同取值范围,选择合适的效用点,即可完成归一化处理。

1.3.2 参数取值与聚合计算

本文使用的对空探测雷达系统指标数据,主要参考的是AN/APY-1型号雷达。对参数层的各个变量值作量化、归一化处理后,可得到二级指标层的效能值,将其按权值累加,可得到系统的综合效能值。参数层各个变量值的典型取值如表3所示。

表3 指标参数变量及典型取值

利用表3提供的参数变量的典型取值可以得到二级指标层的典型效能值,按层次分析法[28]打分得到的全局权重进行累加,可得到典型综合效能值:

(7)

令21项参数指标的取值在典型值基础上进行上下10%的波动,代入效能模型可得到对应的效能输出值。运用敏感性算法对多组效能输出值进行分析处理,即可得到各项雷达系统指标变化时给对空探测雷达系统综合效能带来的影响,为后续的雷达系统优化提供可靠、合理的参考依据。

2 基于FAST方法的敏感性分析

2.1 算法主要思想

FAST方法的主要思想是通过一个转换函数将多维问题转化为一维问题进行求解,为每个输入参数分配对应的特征频率ωi,通过定义一个辅助变量s建立搜索曲线,周期性地探索整个输入空间,使得系统输出的频域特征包含了各输入变量的特征频率成分。最终,输入参数对输出方差的贡献可通过模型输出的傅里叶系数计算得到。主要流程如图2所示。

图2 FAST方法整体思路Fig.2 Overall idea of FAST method

效能评估模型Y=f(x1,x2,…,xn)将模型中的每个参数指标输入xi均与一个特定的频率ωi相关联。ωi为预先选好的特征频率,因此多维输入空间可以通过一组定义良好的参数方程转化为一维变量s,将该参数方程称为转换函数。假设各指标xi在[ai,bi]上均匀分布,转换函数可写为如下形式:

(8)

式中:s是一个标量参数,变化范围为(-∞,+∞)。当s变化时,输入参数xi以特征频率ωi周期性变化,通过搜索曲线周期性地探索整个输入空间,使得系统输出的频域特征包含了各输入变量的变化规律。

根据转换函数的形式,可知无论Y=f(X)形式如何变化,效能评估模型都可表示为s的2π周期函数,即f(s)。将模型进行傅里叶级数展开如下:

(9)

参数Ak和Bk是傅里叶系数,在s∈[-π,+π]的整数频率域上定义为

(10)

(11)

式中:k∈Z={1,2,…,+∞}。

FAST算法可以根据模型输出展开得到的傅里叶系数估计出模型输出的总方差,以及单个输入因子对总方差的贡献,即求得一阶敏感性指数,从而定量得到对空探测雷达系统各项指标单独对其综合效能的影响。

对于FAST方法,给出第i个参数指标xi的一阶敏感性指数(或主效应指数)为

(12)

2.2 特征频率选取

FAST方法利用转换函数将参数指标按不同的特征频率进行采样,把问题转化到频域并进行分析。特征频率集的选取将影响后续敏感性分析的效果,在选取特征频率时,一般遵循如下的基本原则[29]:

(13)

式中:ω为特征频率;A=[a1,a2,…,ai,…,an]为检验向量,ai为任意整数;M为影响阶数,一般取4。式(13)表明,特征频率必须为线性无关的,同时也保证了特征频率的M阶及以下谐波不会对敏感性分析结果产生影响。

文献[30]采用计算机穷举实验得出了5～19维模型下满足基本原则的一组最优特征频率集,该频率集可在保证敏感性分析结果准确性的前提下尽可能减少运算量。本次用于对空探测雷达系统综合效能敏感性分析的共有21项参数指标,同时为适应更加复杂的武器装备敏感性分析要求,需搜索出新的可用的特征频率组。采用穷举法的搜索数目可简要估算为C(n,r),其中n为频率集中最大特征频率的预计值,r为模型维数。以C(150,10)为例,搜索次数达到1015数量级,无法通过普通计算机进行计算,故在此根据文献[30]的计算结果,拟合其变化曲线,初步确定特征频率的范围,再进一步搜索,在较少的计算量下,找到可用的特征频率集。

首先,采用二次函数对提供的频率集中包含频率较多的频率集中的所有频率进行拟合,在此选择15～19维的特征频率集进行拟合,如表4所示。

表4 特征频率集二次多项式拟合

由表4可以看出,各拟合方程对相应特征频率集中频率的拟合程度(R2值)均达到0.99以上,基本可用二次函数初步表示一组特征频率集。

将10～19维特征频率集中的最大特征频率用二次函数进行拟合,得到如下的拟合曲线:

y=5.37x2-72.49x+393.30

(14)

按式(13)预测21维特征频率集拟合方程的3点分别为:P1(21, 1 239.62),P2(1, 123.96),P3(41, 123.96)。经计算,为21项参数指标{x1,x2,…,x21}分配的初始特征频率{ω1,ω2,…,ω21}为{124, 233, 336, 434, 526, 612, 693, 768, 838, 902, 961, 1014, 1 061, 1 103, 1 139, 1 170, 1 195, 1 215, 1 228, 1 237, 1 240},进而按照图3所示的方法进行迭代搜索得到满足准则的特征频率集。

对此结果按特征频率的基本准则进行检验,并记录不满足要求的情况,找出不满足要求次数最多的特征频率,对其在一定范围内进行调整和尝试,进而得到满足准则的特征频率集:{124, 233, 336, 434, 526, 612, 693, 768, 838, 902, 961, 1 014, 1 064, 1 103, 1 139, 1 170, 1 195, 1 215, 1 226, 1 237, 1 245}。采用21维输入指标所对应的特征频率集,利用FAST方法可以在频域内分析对空探测雷达系统综合效能的敏感性。

3 基于Sobol指数法的敏感性分析

3.1 算法主要思想

Sobol指数法的核心思想是基于方差的分解,把函数模型分解为单个参数以及参数之间的组合,通过计算单个输入参数或输入参数集的方差对总输出方差的影响来进行参数的敏感性分析。

假设效能评估模型为Y=f(X),其中X=(x1,x2,…,xn),xi(i=1,2,…,n)服从[0,1]均匀分布Ω=(X|0≤xi≤1)。如果f2(X)可积,那么模型可以分解为

…+f1,2,…,n(x1,x2,…,xn)

(15)

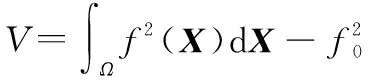
将偏方差与总方差之比作为系统输入指标的各阶敏感性指数,如下所示:

(16)

式中:Si为xi的主效应指数或一阶敏感性指数,表示单个输入xi取值发生波动时,给输出带来的干扰程度;Sij为xi和xj的二阶交互效应指数或二阶敏感性指数,表征两个输入之间的交互作用给输出带来的干扰程度。高阶的敏感性指数表征了多个输入之间的交互作用给输出带来的干扰程度。输入指标xi对对空探测雷达系统综合效能的总影响(即总敏感性指数)可表示为

(17)

图3 特征频率集调整流程Fig.3 Eigenfrequency set adjustment process

3.2 分析计算

(18)

(19)

利用蒙特卡罗模拟的思想,将多维积分问题进行离散求解,效能评估模型输出方差和敏感性指数的估计计算如下:

(20)

参数指标xi的一阶敏感性指数为

(21)

参数指标xi的总敏感性指数为

(22)

参数指标xi和xj的二阶敏感性指数为

(23)

排序前10位的二阶敏感性指数如表5所示,由表5可以看出指标间交互作用较小部分的指标间存在稍大一些的交互作用,但数值均小于0.001。故对对空探测雷达系统进行敏感性分析时,可不考虑交互效应,即主效应与全效应值基本一致,一般只分析主效应即可。

4 敏感性结果分析

通过上述对FAST方法和Sobol指数法的分析,分别利用这两种敏感性分析方法对对空探测雷达系统的综合效能评价模型进行敏感性分析。两种分析方法得到的21维输入指标的敏感性大小如表6所示。

表6 FAST方法和Sobol指数法的敏感性分析结果

续表6

根据表6的数据可知,无论是运用FAST方法或是运用Sobol指数法进行敏感性分析,发射机平均功率、工作频率等指标的主效应指数都较大,半功率点垂直宽度等指标的主效应指数都较小,两种敏感性分析方法的分析结构具有较好的一致性。

采用FAST方法以及Sobol指数法得到的主效应指数对比柱状图如图4所示。观察所有指标的主效应指数大小情况,Sobol指数法与FAST方法的敏感性分析结果基本吻合,且数值误差较小,最大误差为0.002 3,为发射机平均功率对应的主效应指数。

图4 主效应指数大小对比Fig.4 Main effect index sizes’comparison

两种敏感性分析方法所得的主效应指数排序对比如图5所示。FAST方法和Sobol指数法得到的各指标主效应指数排序情况基本吻合。其中,数据处理速度与系统识别技术、平均维修时间与平均无故障时间、旁瓣相消与频率捷变之间主效应指数大小相差很少,出现了排序互换的情况。从整体上看,两种敏感性分析方法获得的敏感性分析结果基本一致。

图5 主效应指数排序对比Fig.5 Main effect index ranking’s comparison

对比两种敏感性分析方法的分析结果,可知功率和频率为对空探测雷达系统的主要影响指标。由雷达原理与实际使用情况可知,雷达发射功率越大,对目标的测量距离越大;在一定范围内,工作频率越高,对目标的分辨能力越好。但在实际设计时会受到T/R组件性能和固态功放器件的限制,目前功率和频率是对空探测雷达系统升级研发的主要研究方向。

5 结 论

对空探测雷达研制经费高昂、研制周期较长,在现有条件下,对其综合效能进行敏感性分析,可以较小代价快速提升对空探测雷达系统的综合效能。本文首先建立了对空探测雷达综合效能的评估体系,采用参数公式、直接定量、专家打分的方式对各个指标进行分析,确定了影响雷达系统综合效能的参数层,构建综合效能的评估模型。为了得到准确可靠的分析结果,本文采用FAST方法和Sobol指数法分别从频域和时域来对综合效能进行敏感性分析。在基于FAST方法进行敏感性分析时,提出了21维输入指标所对应的特征频率集的选取方法;在基于Sobol指数法进行敏感性分析时,考虑了二阶及高阶敏感性指数的影响。对比两种方法的敏感性分析结果,得到功率和频率为对空探测雷达系统的主要影响指标,且两种分析方法的计算结果具有良好的一致性。在后续分析时,效能评估模型的形式应根据不同的任务需求进行修整,也可进一步探索其他敏感性分析方法在效能评估上的应用情况。