基于子阵级处理的宽带非规则子阵相控阵鲁棒性干扰抑制

陈吉源, 徐振海, 肖顺平

(国防科技大学电子科学学院电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410073)

0 引 言

相控阵技术在雷达、通信、遥感等领域广泛应用,特别是在预警探测、目标识别等方面大放异彩[1]。现代化的雷达装备需要满足多功能、大带宽及数字化等要求,这将给阵列雷达系统的整体成本及工程复杂度带来巨大的挑战[2-3]。子阵技术是实现相控阵性能和成本折中的一项关键技术,其中非规则子阵技术凭借其模块化可重构的特性以及全寿命周期低成本的优势成为子阵技术的新一轮研究热点[4-6]。目前,针对该技术的研究主要集中在窄带情况下的子阵设计和处理,并已取得较大的进展[7-10]。随着对目标精密跟踪、高分辨成像、目标特征感知和识别等要求的不断提高,相控阵雷达系统对工作带宽的要求也不断提升[11-12]。

在日益复杂的电磁环境中,伴随着现代雷达对抗技术的成熟,宽带相控阵雷达的工作环境也将越来越恶劣[13]。相比窄带体制,宽带相控阵面临着更加复杂的干扰威胁。例如,伴随目标回波同时出现的有源压制干扰,接收机在整个信号频谱内都接收到干扰,即宽带阻塞式干扰以及与目标回波高度相似的欺骗干扰[14]。另外,包括扫频式干扰和扫描式干扰在内的窄带干扰也是目前雷达对抗中常见的干扰样式[15]。这些干扰组合成复杂的宽窄带组合干扰,对宽带雷达实现目标高分辨成像、识别带来了极大的困难。为应对宽带波束色散和常规窄带方法在宽带相控阵雷达中抗干扰性能不足的问题,目前主要有自适应抽头延时[16-17]、频域子带处理[18-19]两种典型的处理方式。由于多抽头处理和多子带处理增加了系统运行复杂度以及硬件实现难度,在实际相控阵雷达系统中难以实时处理。对于宽带相控阵中最常见的宽带线性调频(linear frequency modulation, LFM)信号,其特殊的调频特性可以采用Stretch处理方法实现脉冲压缩,有效地降低处理带宽[20]。过去的研究大多数针对模拟Stretch预处理,随着高速模数转换器和集成电路的发展,射频直采和数字Stretch处理在宽带阵列中的研究也逐渐增多[21]。然而,Stretch处理后的窄带信号模型与传统窄带模型存在差异,直接采用窄带处理方式会造成性能损失。对于非规则子阵相控阵,以子阵级实现数字化处理能够有效实现雷达系统成本和性能的平衡,但目前关于子阵级Stretch处理干扰抑制的研究较少。

此外,在实际阵列中还存在一些不可避免的误差,这些误差会导致阵列流行误差和性能降低。例如,由元器件加工带来的差异、由阵元安装中存在的布阵误差带来的幅度和相位误差,以及各通道的接收信号采样存在的误差和由某些阵元失效带来的随机幅相误差[22]。多功能宽带相控阵雷达一般具有多个工作模式,在窄带模式下实现目标检测、跟踪和参数测量,在宽带模式下进行成像。受限于测量精度和目标运动影响,窄带模式下获得的目标距离和方位信息与真实值存在一定误差,这进一步导致导向矢量失配。对于宽带非规则子阵相控阵,子阵级处理也会带来难以避免的误差。这些误差会使得阵列波束形成后的输出信号信干噪比(signal to interference and noise ratio, SINR)严重下降。近年来,研究人员提出了多种在复杂环境下保持鲁棒性的波束形成方法,包括对角加载[23]、子空间分解[24]、最坏情况最佳化(worst-case performance optimization, WCPO)[25]等方法。Gu等[26]提出了性能更佳的协方差矩阵重构方法,该方法只采集目标期望信号空间区域之外的信息,即可获得干扰加噪声协方差矩阵,但在阵列流型存在误差时该方法会失效[27]。在此基础上,涌现出了一系列基于协方差矩阵重构的改进波束形成算法[28-29],这些方法在特定条件下能够获得较好的性能,然而这些方法计算量均较大,对于大规模阵列难以实时处理,且都只应用在阵元级处理中。

针对以上问题,本文围绕宽带非规则子阵相控阵的子阵级Stretch处理和鲁棒性自适应波束形成方法展开研究。首先,建立存在误差的子阵级回波模型,将各种误差的影响转化为各通道的随机幅相误差。然后,进行子阵级Stretch处理,包括混频、抽取、滤波和时变相位加权处理几个重要步骤。进一步地,利用处理后的数据和先验信息校正干扰子区间内的阵列流型,通过改进的谱分离方法重构面阵的干扰加噪声协方差矩阵,利用对角加载的思想获得最优权值。最后,加权合成各通道信号,经过快速傅里叶变换(fast Fourier transform, FFT)获得目标一维距离像。文中通过多个实验验证了非规则子阵较规则子阵的优势,以及所提鲁棒性自适应波束形成算法的有效性。

1 存在误差的子阵级回波模型

宽带相控阵雷达发射的LFM信号可以表示为

(1)

式中:f0、μ、T0、B分别表示信号载频、调频斜率、脉宽和带宽;B=μT0;rect(·)表示门信号,即

假设一个宽带非规则子阵相控阵阵面中有N个阵元,则在t时刻,阵面接收到的信号可以表示为x(t)=(x1(t),…,xk(t),…,xN(t))。其中,xk(t)表示第k个阵元接收到的信号。目标入射方向为θs,目标与参考阵元的距离为Rs,第k个阵元的接收信号可以表示为

(2)

若该阵面被划分为M个非规则子阵,子阵和阵元之间的转换矩阵为TN×M,阵元级无加权处理,则T是一个仅包含0～1元素的矩阵。接收到的信号在子阵级合成后进行处理,可以将每个子阵视为一个通道。子阵级接收信号可以表示为

xsub(t)=TH·x(t)

(3)

对每个子阵进行数字采样,则第m个子阵在第n时刻接收到的信号为

(4)

式中:Nm表示第m个子阵包含的阵元个数;Ts表示采样间隔。将第n时刻阵列接收的数据矢量化表示为

xsub(n)=THx(n)=TH(s(n)+i(n)+n(n))

(5)

式中:xsub(n)=[xsub1(n),xsub2(n),…,xsubm(n)]T代表子阵级接收信号矢量;x(n)=[x1(n),x2(n),…,xn(n)]T代表阵元级接收信号矢量;s(n)=[s1(n),s2(n),…,sN(n)]T、i(n)=[i1(n),i2(n),…,iN(n)]T和n(n)=[n1(n),n2(n),…,nN(n)]T分别表示目标信号、干扰和噪声矢量。

在干扰抑制中通过空域处理滤除干扰信号,只保留期望目标信号,获得最优SINR。但在实际阵列中,存在一些不可避免的误差,这些误差会导致性能降低。对于第m个通道,假设随机幅度和相位可以表示为αm和βm,且通道中干扰信号和目标信号的随机幅度和相位误差相同。故接收的信号可以表示为

(6)

(7)

2 子阵级数字Stretch处理

为实现数字Stretch处理,需要产生数字域参考信号,然后与回波信号做差频处理。参考信号可以表示为

(8)

式中:tr=2Rr/c,Rr表示参考距离,一般取目标散射中心和参考阵元之间的距离,可通过窄带模式测得;Tr为参考信号脉宽(一般取Tr>T0);r0=(Tr-T0)c/2为距离窗口,其大小取决于目标的尺寸和测距精度。

对子阵回波信号和参考信号做差频处理并进行低通滤波处理后,有

(9)

从式(9)可以看出,经过差频处理之后,目标信号变为多个单频信号的合成信号,这些单频信号的频率可以表示为fsubm={μ(tΔ-τk)|k∈[1,Nm]}。前面所取距离窗一般大于目标距离与参考距离之差,因此差频处理后的最大有效带宽为Bd=μ(2r0+L)/c,其中L表示阵列尺寸。一般情况下,发射信号脉宽远大于距离窗口和阵列尺寸对应的时宽,因此信号带宽B远大于差频处理后的有效带宽Bd,则射频直接采样的采样间隔取决于信号带宽B。差频处理后的信号带宽大幅降低,为有效降低处理数据量,可以进行数据抽取。差频处理后需先进行滤波处理,滤波器的通带截止频率Bp>Bd,对应的数据抽取倍数则小于D=fs/Bd。为简化表达,抽取后的采样间隔仍用Ts表示,则式(9)在形式上无变化。通过以上分析也可以看出,在无需射频直接采样的应用中,可在子阵级完成模拟差频处理和滤波等处理后再通过A/D(analog/digital)数字采样,这样可以大幅降低数据采样率和对A/D转化器的带宽要求。当然,数字处理可以有效减少模拟期间带来的失真,处理更加灵活。

为了更好观察子阵之间的相位关系,将式(9)改写为如下形式:

(10)

(11)

从式(11)可以看出,Φ(n)与τk无关,不随k变化。exp{j2πf0τk}可视为导向矢量。Ψk(n)是一个多项式,与阵元间时间差τk和时间变量n有关。对应一个固定方位角,阵元间相位差时变将导致子阵间相位差时变,这与窄带阵列中阵元相位差恒定不符,因此需要对Ψk(n)进行补偿以消除时变相位差的影响。

(12)

(13)

(14)

(15)

因此,可将式(14)简化为

(16)

(17)

将式(17)写为向量形式:

(18)

(19)

式中:

表示阵元级实际的导向矢量。根据窄带测量估计出来的子阵级导向矢量为

(20)

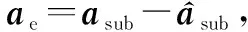
(21)

对式(21)求模值平方可得

(22)

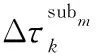
(23)

式中:t′=nTs-ts。故,可得

(24)

因此,实际子阵导向矢量可以通过不确定集表示:

Ω{asub|≤ε0}

(25)

该误差约束也被称为球形不确定集,可根据先验信息获得。通过上面的推导和分析可以看出,经过子阵级数字Stretch处理以及时变加权补偿处理,子阵级的目标信号可以看作窄带信号,但子阵级的导向矢量存在误差,属于一个不确定集。经典Capon波束形成模型为

(26)

(27)

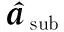
3 鲁棒性自适应波束形成

利用经典Capon空间谱估计技术可以粗略地估计干扰的到达方位角,描述空间的信号分布情况。面阵的Capon空间谱基本公式为

(28)

(29)

图1 导向矢量失配和区域划分示意图Fig.1 Schematic diagram of steering vector mismatch and region division

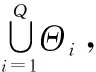
(30)

(31)

式中:εI是一个反应阵列流行误差程度的边界值,可参考式(24)的取值。这里利用拉格朗日算子法求解该问题。

(32)

式中:η为拉格朗日乘子。最终,可以获得最优的导向矢量为

(33)

将式(33)代入式(37)的约束条件中,可得关于η的方程:

(34)

求解式(34)首先需确定解的上下界,然后利用二分法或牛顿迭代法即可通过求解获得η的值,将η的值代入式(33)即可估计出准确的导向矢量。故最终可以准确获得干扰加噪声协方差矩阵:

(35)

式中:Ωint∈Θint。在实际中,求解式(35)可以离散化处理。因此,波束形成问题变为

(36)

可以获得最优权值为

(37)

式中:λ是对角加载因子,可以通过牛顿法获得。总结前面的自适应处理过程,可得算法流程如算法1所示。

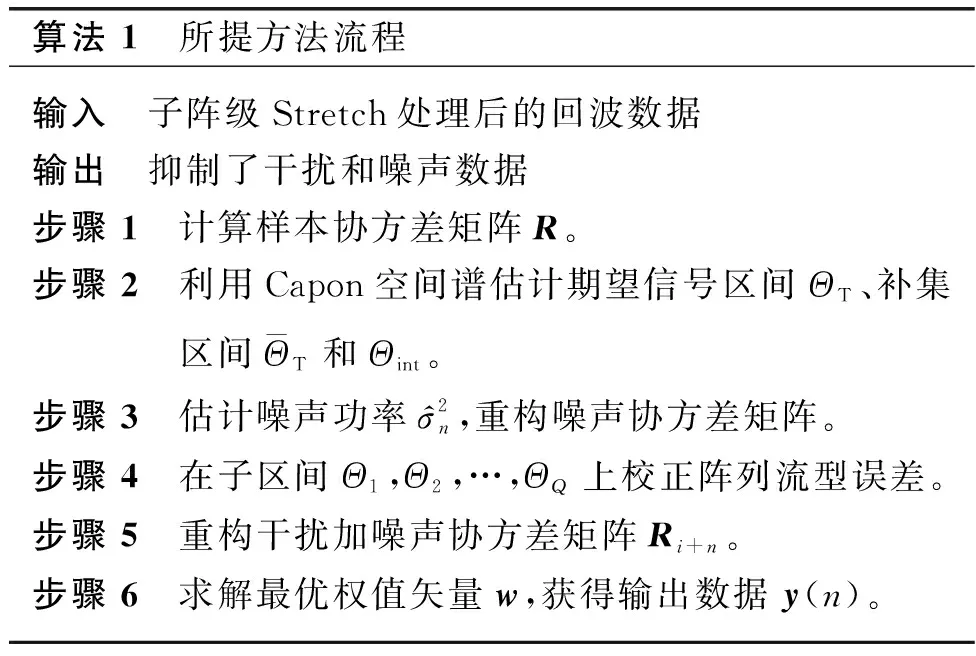
算法 1 所提方法流程输入 子阵级Stretch处理后的回波数据输出 抑制了干扰和噪声数据步骤 1 计算样本协方差矩阵R。步骤 2 利用Capon空间谱估计期望信号区间ΘT、补集区间ΘT和Θint。步骤 3 估计噪声功率σ^2n,重构噪声协方差矩阵。步骤 4 在子区间Θ1,Θ2,…,ΘQ上校正阵列流型误差。步骤 5 重构干扰加噪声协方差矩阵Ri+n。步骤 6 求解最优权值矢量w,获得输出数据y(n)。

最终波束形成器的输出信号通过对数据使用获得的权矢量进行加权获得

(38)

对输出信号进行FFT处理可以获得目标的一维距离像。

总结前面所有的处理流程,结合所推导的过程给出如图2所示的处理流程图,其中数字Stretch处理过程包含了混频处理、抽取、滤波以及时变加权处理过程。通过Stretch处理后获得的数据进行鲁棒性自适应波束形成,即执行算法1的流程,获得经最优权值加权抑制了干扰和噪声的输出信号,最终通过FFT处理即可获得目标的一维距离像。

图2 阵列接收信号处理流程Fig.2 Procedure of array receiving signal processing

4 实验结果与分析

实验中的阵面规模为64×64,子阵大小为8单元子阵,子阵类型分别为2×4矩形子阵和L型8单元非规则子阵。当子阵类型为矩形子阵时,通过规则拼接获得整个阵面;当子阵类型为非规则子阵时,采用分层子阵设计策略获得阵面结构[31],如图3所示。阵面工作在X波段,中心频率为10 GHz,发射信号为宽带LFM信号,阵面和信号的基本参数设置如表1所示。下面根据不同的子阵类型、干扰类型、SINR、目标类型、SNR对所提方法的性能进行仿真验证和分析。

图3 非规则子阵阵面结构Fig.3 Structure of irregular subarrayed array

表1 仿真参数设置

4.1 宽带规则子阵相控阵

为了对比宽带非规则子阵相控阵的性能,首先仿真子阵类型为矩形子阵的宽带相控阵空域方向图和时域干扰抑制效果。宽带相控阵易受宽带阻塞式干扰,也会受到窄带扫频式干扰或扫描式干扰,除此之外可能还会受到支援式欺骗干扰,例如常见的间歇采样转发式干扰。

实验 1

依据不同宽带干扰类型和干扰来波方向,通过4个仿真实验验证不同子阵的性能和所提方法的有效性。首先假设空间中有一个窄带干扰和一个宽带噪声干扰的组合干扰信号抵达阵列,两个干扰的参数设置如表2所示。

表2 两个干扰的参数设置(实验1)

阵列的幅相误差均服从高斯分布,先固定随机幅相误差的标准差为0.1和5°。目标实际方位与期望方位在两个方向均有1°的差异。根据提出的处理流程和方法,首先获得子阵级回波数据,经与参考信号混频和滤波后进行时变加权相位补偿,利用补偿后的数据实现鲁棒性自适应波束形成(robust adaptive beamforming, RABF)获得最优权值,实现回波数据中的干扰抑制。

经过鲁棒性自适应波束形成处理获得阵面的正弦空间方向图,其中雷达天线坐标系下u=sinθcosφ,v=sinφ,结果如图4(a)所示,两个干扰方位均能形成零陷,即图中两个红色实线圆圈内的位置。将输出数据与获得的最优权值加权并进行FFT处理,最终获得目标的一维距离像,如图4(b)所示。可以看出,处理前干扰和噪声将目标淹没,无法检测出位于10 m处的目标信号,经鲁棒性自适应波束形成处理可以有效抑制干扰和噪声,目标可以非常清晰地被识别出来,且旁瓣电平被压低。

图4 规则子阵阵面实验1结果Fig.4 Experiment 1 results of regular subarrayed array

实验 2

然而,阵面由矩形子阵规则拼接而成,子阵级处理的阵面方向图中不可避免地存在由栅瓣引起的高副瓣,如图4(a)中粉色椭圆圈内位置所示。仅在子阵级加权处理无法抑制这些方位的高副瓣,如果干扰从这些角度抵达阵列,那么干扰信号将难以被抑制。为验证该现象,修改干扰的方位角为栅瓣所在位置,干扰1的方位在uv域为(-0.88,0.17),干扰2的方位为(0.17,-0.35)。其余参数和前面设置相同,经过仿真实验2可以获得如图5所示的结果。

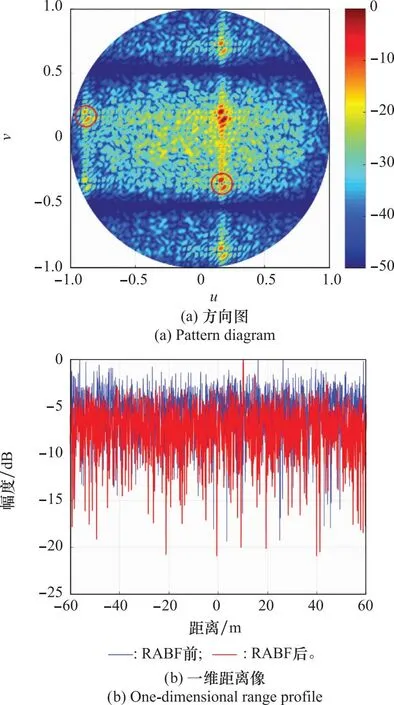
图5 规则子阵阵面实验2结果Fig.5 Experiment 2 results of regular subarrayed array

从实验2结果可以看出,图5(a)中的方向图主瓣发生畸变和分裂,造成阵列增益损失;在干扰处高栅瓣也发生分裂,方向图零陷深度变浅,干扰抑制效果变差。图5(b)所示的一维距离像可以直观地展示脉压后的干扰抑制效果,干扰和噪声对检测造成较大影响,难以有效检测出目标。

实验 3

实验1中的干扰2为一个宽带噪声干扰,在实验3中将该干扰替换为一个和目标信号相同的宽带干扰信号,该干扰的参数和实验1保持一致,如表3所示。宽带干扰为宽带LFM信号,中心频率为10 GHz,带宽为1 GHz,脉宽为50 ms。实验获得方向图和一维距离像如图6所示。

表3 两个干扰参数的设置(实验3)

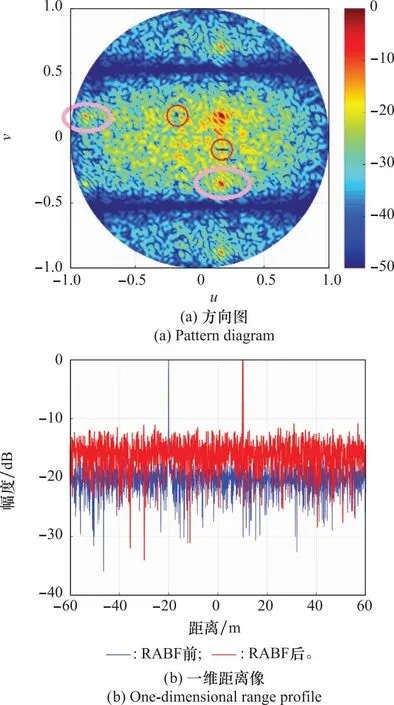
图6 规则子阵阵面实验3结果Fig.6 Experiment 3 results of regular subarrayed array

从实验3结果可以看出,阵列方向图在两个干扰方位处形成零陷;未经RABF处理的一维距离像在干扰2的位置处产生虚假目标,完全无法检测出目标。经过RABF处理后,可以在目标位置处清晰检测出目标。

实验 4

当干扰来波位于图6(a)中红色虚线圆圈,即栅瓣位置处,设置与实验3相同的参数进行实验4,则可获得阵列方向图和一维距离像,如图7所示。

图7 规则子阵阵面实验4结果Fig.7 Experiment 4 results of regular subarrayed array

实验4结果和实验2类似,阵列的方向图主瓣发生分裂和畸变,两个干扰处零陷深度变浅。经RABF处理后,一维距离像在目标处出现尖峰,但干扰位置处的虚假目标尖峰依旧很高,同时副瓣电平整体较高,说明干扰抑制能力大幅降低。

通过实验2和实验4可以看出,规则子阵会导致阵列方向图中产生高副瓣电平,且这些由栅瓣引起的高副瓣电平难以通过子阵级加权处理实现抑制;当干扰从栅瓣进入,会造成方向图发生畸变,降低阵列增益和干扰抑制效果。

4.2 宽带非规则子阵相控阵

对于宽带非规则子阵阵面,和规则子阵阵面一样完成4个仿真实验,以验证该体制的优势以及所提方法的有效性。4个实验的参数设置分别对应前面的规则子阵阵面。首先给出非规则子阵阵面实验1的实验结果,如图8所示。方向图中在干扰来波方位处形成零陷,即图8(a)中红色圆圈内。相比规则子阵阵面,非规则子阵方向图的主瓣波束附近的副瓣更低,主瓣增益损失更小。经RABF处理后的一维距离像中干扰被有效抑制,可清晰检测和辨识目标对应的峰,且旁瓣压低至-10 dB水平。

图8 非规则子阵阵面实验1结果Fig.8 Experiment 1 results of irregular subarrayed array

非规则子阵阵面方向图中仍然存在较高的副瓣,如图8(a)中红色虚线圆圈所标记。实验2的干扰方位来自高副瓣位置,干扰1的方位在UV域为(-0.35,0.17),干扰2的方位为(0.17,-0.35),实验结果如图9所示。可以看出,在非规则子阵阵面方向图中主瓣波束未发生畸变,在高副瓣位置仍然可以形成零陷,来自该方位的干扰可以被有效抑制。同样,在所获得的一维距离像中可以清晰检测到目标对应的尖峰,干扰和噪声被压制。

图9 非规则子阵阵面实验2结果Fig.9 Experiment 2 results of irregular subarrayed array

实验3的结果如图10所示,无论是方向图还是一维距离像结果都验证了所提方法的有效性。实验4中干扰来波方位与实验2相同,实验结果中的方向图主瓣无畸变,如图11所示,且主瓣附近副瓣电平较规则子阵阵面方向图较低,在高副瓣位置形成零陷;在对应的一维距离像中目标可以被完全检测出来,旁瓣水平低于10 dB,干扰抑制效果较好。

图10 非规则子阵阵面实验3结果Fig.10 Experiment 3 results of irregular subarrayed array

图11 非规则子阵阵面实验4结果Fig.11 Experiment 4 results of irregular subarrayed array

通过4个仿真实验可以看出,采用非规则子阵的阵面性能更为突出,RABF处理后方向图中主瓣能够保形,主瓣附近的副瓣较低,阵列增益更高;同时不存在导致干扰抑制效果变差的方位角度,更有利于实际使用。

4.3 多散射点目标实验结果

宽带相控阵雷达可以获得较高的距离分辨力,小于目标物理尺寸,则实际目标通常可以采用散射点模型,即在距离维有多个强散射点。假设目标在距离维有3个强散射点,距离分别为9,10,12;对应的散射强度分别为1,2,1.5。保持非规则子阵阵面和信号的参数设置不变,将单点目标变为多个散射点目标。如前文所述,将该部分仿真仍然分为两部分,实验1首先仿真干扰2为宽带噪声干扰的情况,其他参数与第4.2节中的实验1相同。由于干扰和噪声与前文单目标实验相同,且目标方位角度不发生变化,则经RABF处理后的方向图与图8(a)一样,目标的一维距离像如图12所示,黑色圆圈内为处理后的一维距离像,放大后如图12(b)所示。

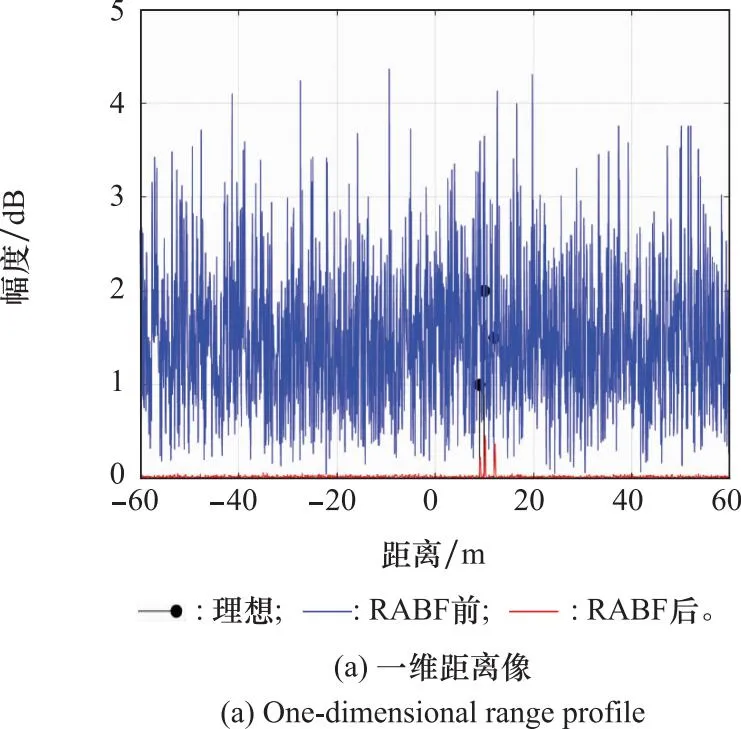
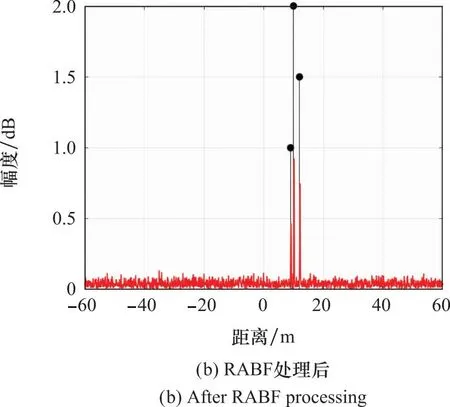
图12 多散射点目标实验1一维距离像Fig.12 One-dimensional range profile of multi-scattering target in experiment 1

从实验结果可以看出,在RABF处理后可以清晰获得目标散射点对应的峰,而在RABF处理前则被干扰和噪声完全覆盖,无法检测出目标信号。从图12(b)可以看出,所获得的一维距离像中目标散射点的强度较理想值有一定损失,各通道的相位误差是造成能量损失的根本原因,相位误差主要来源于子阵级处理过程中的时变相位补偿以及各通道随机幅相误差。

实验2的仿真主要将干扰2替换为宽带欺骗干扰信号,该干扰与目标信号具有相同的参数,其他参数设置与第4.2节实验3相同。假设干扰信号先于目标到达阵面,距离分别为-11,-10,-8。此时的干扰2与单目标中的干扰2不同,经RABF处理后获得的阵面方向图和归一化的一维距离像如图13所示。阵列方向图与前面单目标情况类似,在干扰方位形成零陷,主瓣波束无畸变;图13(b)所示的一维距离像在RABF处理前无法识别目标,湮没在干扰和噪声中,获得了较好的欺骗效果。处理后目标对应的峰值可以清晰地获得,且干扰和噪声信号被压制在-20 dB水平。

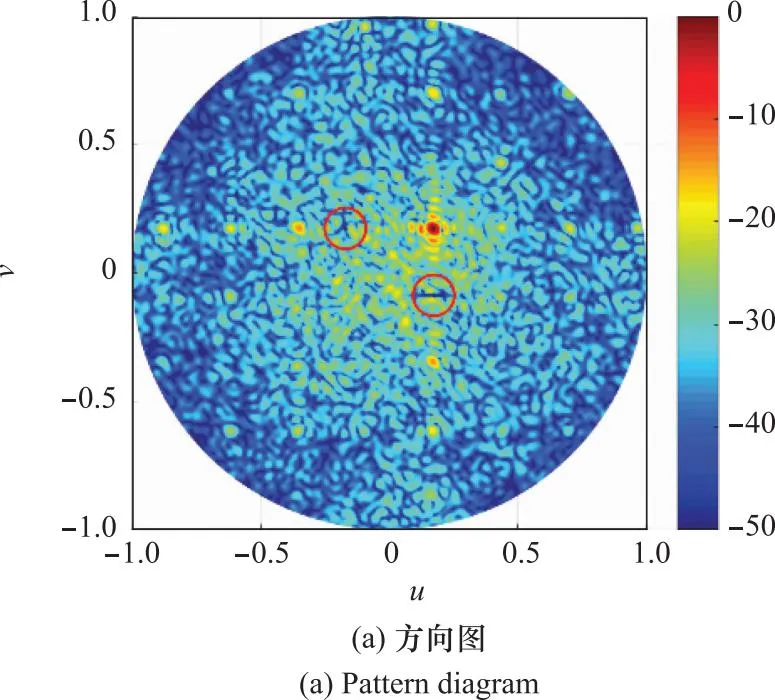
图13 多散射点目标实验2结果Fig.13 Experiment 2 results of multi-scattering target

如同实验1,这里进一步给出了RABF处理前后的一维距离像。图14(a)中干扰的强度远远大于目标信号强度,成像结果中的虚假目标会影响目标检测和识别。黑色圆圈内为处理后的一维距离像,放大后如图14(b)所示。经过RABF处理后,干扰得到了有效抑制,形成多个散射点对应的尖峰。与实验1类似,目标散射点能力存在一定损失。

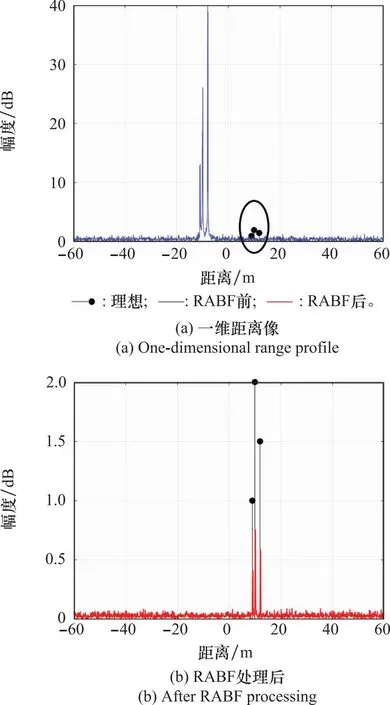
图14 多散射点目标实验2一维距离像Fig.14 One-dimensional range profile of multi-scattering target in experiment 2

4.4 干扰抑制性能分析

本部分实验研究不同误差情况下的干扰抑制性能,比较几种经典方法的干扰抑制性能,每个点经过200次蒙特卡罗实验得到。设置如第4.2节中实验1的参数,在输入SNR从-20 dB变化到20 dB的阵列输出SINR的变化情况,结果如图15所示。可以看出,相比已有的SMI算法、对角加载方法、子空间分解方法、WCPO方法,所提方法输出SINR更高,干扰抑制性能更好。

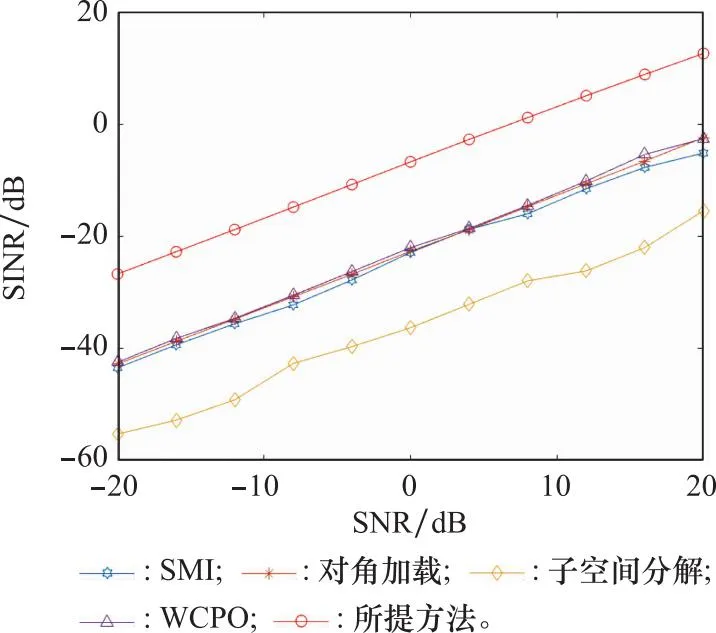
图15 输出SINR随输入SNR的变化情况Fig.15 Variation of output SINR with input SNR

进一步固定输入SNR为-10 dB,在随机相位误差标准差为5°的情况下,随机幅度误差标准差的变化范围为[0,0.4],输出SINR的变化情况如图16所示。所提方法的输出性能明显优于其他方法,高于对角加载方法8 dB左右。同时可以看出,随机幅度误差标准差的变化对这些方法的输出SINR影响不大,实验结果无明显变化。在图17中,固定随机幅度误差标准差为0.1,随机相位误差的标准差从0°变化到10°,所提方法输出SINR无明显变化,但其他方法都下降了约3 dB。从图16和图17的结果可以看出,随机幅度和相位误差的标准差增大会导致干扰抑制性能降低。

图16 输出SINR随幅度误差标准差的变化情况Fig.16 Variation of output SINR with standard deviation of amplitude error

图17 输出SINR随相位误差标准差的变化情况Fig.17 Variation of output SINR with standard deviation of phase error

此外,本文还分析了期望信号方位与目标实际方位存在误差时阵列的干扰抑制性能变化情况。由于在两个方位同时变化时难以对比这几种方法的性能,因此固定目标的俯仰向为0°,方位向为10°,假设误差只存在于方位向。固定输入SNR为-10 dB,随机幅度、相位误差的标准差分别为0.1°和5°,目标的方位向误差角度从0°变化到5°,不同方法的输出SINR变化情况如图18所示。所提方法的输出SINR在低SNR时较其他方法更高,但随着目标期望角度误差增大,SINR值也逐渐下降,当角度误差达到4°以上时,所提方法的干扰抑制性能与其他方法相比无明显差距。整体上看,角度误差的增大会导致SINR值降低,这也意味着干扰抑制性能下降。

图18 输出SINR随期望信号方位角误差的变化情况Fig.18 Variation of output SINR with desired signal azimuth error

从本节的实验结果可以看出,相比其他已有的方法,所提方法的性能更好,稳定性更高,且在重构干扰协方差矩阵时计算量更低。在该仿真条件下,已有的方法中子空间分解性能最差,对角加载方法性能更好。

5 结 论

本文针对宽带非规则子阵相控阵在存在通道误差和在复杂干扰环境下性能变差的情况,基于子阵级Stretch处理提出协方差矩阵重构的鲁棒性干扰抑制方法,主要步骤包括面阵的子阵级回波模型建立、子阵级数字Stretch处理和改进的基于谱分离协方差矩阵重构的鲁棒性自适应波束形成方法。该处理过程有效降低了数字化采样通道数量和计算量,且能够在存在误差的情况下较好地抑制不同宽窄带组合干扰。通过多个实验对比分析,本文方法具有更好的性能和适用性:① 对比规则子阵阵面,非规则子阵阵面干扰抑制性能更好,方向图中不存在干扰难以抑制的方位角度;② 在不同目标和组合干扰类型下都能较好地抑制干扰;③ 能获得更高的输出SINR,对多种存在误差的情况具有较强鲁棒性。