Sylvester-Kac矩阵的奇异值所在区间估计
白明月,秦建国
(郑州商学院 通识教育中心,河南 巩义 451200)
设P是如下形式的(n+1)×(n+1)的三对角矩阵
(1)
其中n是一个非负整数.这个矩阵在统计力学和量子物理学中应用比较多,比如,布朗运动、在超大立体上随机漫步和氢原子的斯塔克效应等许多问题中.SYLVESTER JJ[1]猜想出计算P的特征值的公式λi=n-2i,i=0,1,2,…,n.MUIR T[2]第一个给出了此公式的证明.矩阵P的对称形式出现在SCHRODINGER E[3]的论文中,这些结果包含了波动力学的基础.后来,KAC M[4]应用生成函数的办法,证明Sylvester公式,还给出了相应特征向量的分量的多项式表示.VINCZE I[5]和近些年的EDELMAN A[6]通过把P表示成适当定义的函数空间上的微分算子的矩阵,给出了Sylvester公式简洁的证明.长期以来,关于矩阵P的谱分解的研究可谓如火如荼,但关于矩阵P的奇异值分解的研究却并不充分.BOROS T[7]和CARLOS M[8]分别给出了在n=2m,即P的阶数是奇数时,P至少有m+1个奇异值的平方是正整数这一猜想的证明.近年,人们对于矩阵奇异值的研究一直没有间断[9].本文给出矩阵P的其余m个奇异值存在的区间估计.

1 基本结果
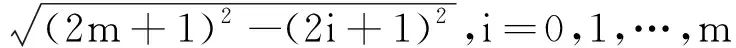
(2)
证明先考虑m为奇数的情形.
下面利用置换矩阵将P化为四分块矩阵.
令Π=[e2,e4,…,e2m,e1,e3,e5,…,e2m+1],这里
ei=(0,…,0,1,0,…,0),
第i个位置元素是1,其余元素全为零,长度为2m+1的第i个单位向量,i=1,2,…,2m+1.不难验证
(3)
(3)式中Q∈R(m+1)×m和S∈Rm×(m+1)分别是如下形式的矩阵
又因为P、Q、S均为实矩阵,有
(4)
所以,矩阵QQ*=QQT和SS*=SST的所有特征值的算术平方根构成矩阵P的奇异值集合.而矩阵QQT的特征值或Q的奇异值已由BOROS T[7]给出.现在只需要讨论矩阵SST的特征值问题.由于目前尚未找到计算P的这些奇异值的公式,下面给出其存在的区间估计,为此计算SST,
下面利用关于矩阵特征值的Gerschgorin圆盘定理[10],估计SST的特征值所属范围.由于SST是一个m阶的三对角矩阵,应用Gerschgorin圆盘定理,加之SST的非零元素仅位于主对角线和紧邻该主对角线的上和下2条对角线上,只需考虑SST的这3条对角线上的元素.由于SST的元素又满足条件
(SST)i,j=(SST)m-i+1,m-j+1,i,j=1,2,…,m,
(5)

Dk={z||z-[k2+(2m-k)2]|≤k[2m-(k-2)]+(k+2)(2m-k)},k=3,5,…,m.
而第一行的元素不能用上式,把第一行所对应的圆盘单列,于是可知SST的特征值必然位于下述圆盘的并集之内
∪{z||z-[1+(2m-1)2]|≤3(2m-1)}.
(6)
但(SST)*=SST,表示矩阵SST是一个Hermitian矩阵,因此它的特征值是实数,即它的特征值全在复平面的实数轴上,这时(6)式中表示复变量的z可以换为表示实变量的x.进一步,矩阵SST还是一个半正定矩阵,从而是一个Hermitian半正定矩阵,它的特征值全部非负.于是,上述全部闭圆盘可以全部改为闭区间.
将(6)式中的圆盘进一步化简,发现上述m个圆盘(闭区间)具有逐个包含关系.
事实上,
即
先比较除第一行外所对应的区间的包含关系,由此取∀k1,k2∈{3,5,…,m},k1 由于这2个区间 D1=[4[(m-k1)2-m],4m(m+1)],D2=[4[(m-k2)2-m],4m(m+1)] 的右端点相同,而左端点之差是 4[(m-k1)2-m]-4[(m-k2)2-m]=4[2m-(k1+k2)](k2-k1), 由于k1,k2∈{3,5,…,m},k1 [0,4m(m+1)]⊂R. (7) 再将此区间与第一个(圆盘)区间[4m2-10m+5,4m2+2m-1]比较,当m≥3时, 0 所以,第一行所对应(圆盘)区间包含在(7)式所表示的区间内.得到P的另外m个奇异值应该位于(7)式所表示的区间[0,4m(m+1)]. (7)式所表示的区间的左端点还可以改为开区间.由此,下面证明矩阵SST是可逆矩阵,那样SST就没有零特征值,从而可以将(7)式的左闭改为左开. 仿造证明方程组STx=0和方程组SSTx=0同解的办法可以证明 秩(ST)=秩(SST). 再由矩阵S可知,SST的阶数m=秩(S)=秩(ST)=秩(SST). 这表明0∉σ(SST).因此SST的特征值所属区间应是将(7)式中闭区间的左闭改为左开,即SST的特征值所属范围估计是 σ(SST)⊂(0,4m(m+1)]⊂R. (8) P的其余m个奇异值所属范围是 (9) 接下来,处理m为偶数的情形.这时,利用(3)式,仍将计算SST的结果记为 仿m为奇数的情形可以证明SST的特征值也是位于区间 证毕. 定理2非负矩阵SST的谱半径ρ(SST)满足下述界限: 4m2+2m-1<ρ(SST)<4m2+4m. (10) 证明首先,指出SST是一个m阶非负不可约方阵.在平面上取m个不同点,标以号码1,2,…,m,作为矩阵SST的结点,然后画出SST的有向图Γ(SST),如下所示: 图1 SST的有向图Γ(SST) 显然,对Γ(SST)的任何一对有序结点(i,j)都有一条由有向弧线组成的有向路径 连接结点i与j,因此矩阵SST的有向图Γ(SST)是强连接的,即SST是一个非负不可约矩阵.这样关于SST谱半径ρ(SST)的范围估计,只有2种情况可能发生. 由于SST的第一行元素之和为4m2+2m-1,其余各行元素之和均为4m2+4m,SST的各个行和并不相等,这就排除了第一种可能,即排除了 发生的可能性. 剩下的唯一的可能性是 即 4m2+2m-1<ρ(SST)<4m2+4m. 区分m分别是奇数和偶数2种情况,研究了n=2m时Sylvester-Kac矩阵的另外m个奇异值所在区间估计及其谱半径所在区间的估计.(1)式中的矩阵P与文献[11-12]中的矩阵A同为可对角化矩阵,但后者可以和对角矩阵酉相似,而P不可以和对角矩阵酉相似.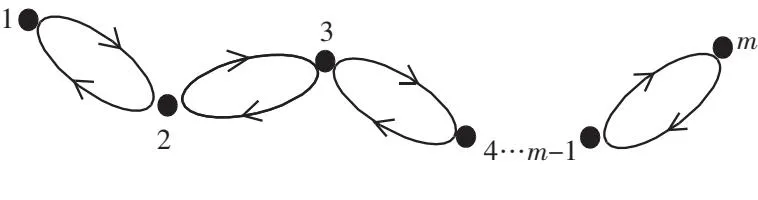

2 结语

