含孔板微通道内随流气泡运动的两相格子Boltzmann模拟

丁弘毅, 王治云, 赵敬帅, 王 楠, 娄 钦

(上海理工大学 能源与动力工程学院, 上海 200093)

0 引 言

随着能源利用的发展,含气泡运动的两相流系统在自然界和工程应用中广泛存在,如舰船废气隐蔽排放、页岩油开发、生物柴油制备、CO2地质封存等[1-2],这些过程都存在气泡通过孔板的现象．撞击孔板过程中,气泡在表面张力和惯性力的作用下发生形变甚至破碎现象,涉及复杂的界面演化问题[3]．随着计算科学的快速发展,此类流动的数值模拟能揭示气泡破裂聚合的机理,为提高两相流传热传质效率提供理论依据,是实验研究的重要补充[4],具有重要的工程实践和学术研究意义[5]．

许多研究者都对微通道内的气泡流动问题进行过实验研究．Hallmark等[6]研究了含孔板矩形通道内,气泡在高黏度Newton流体中上升时的形状变化,发现气泡穿越孔板后演化为“新月形”．Dawson等[7]研究了体积流量恒定条件下气泡在狭窄微通道内传播变形的过程,发现该过程由黏性剪切力主导,从而影响气泡前后部的曲率变化规律．Losi等[8]对气泡在水平管道中的运动进行了深入实验,分析了黏度对气泡在水平管道中漂移速度和形态的影响．Wu等[9]研究了孔喉微结构中的气泡破碎现象,实验表明随着孔径比、喉长、母泡速度和毛细数的增大,子泡大小呈线性或指数减小趋势．

过去三十余年,作为一种介观数值计算方法,格子Boltzmann方法(lattice Boltzmann method, LBM)在模拟多相流时具有算法简单、并行效率高和复杂边界易于实现等显著优势[10],因此开发能够模拟大密度比流场的多相流模型在LBM研究者中是一个很有吸引力的课题[1]．Inamuro等[11]提出了第一个基于自由能方法的LB模型,实现了密度比高达1 000的液滴与气泡模拟计算．随后Yi和Xing[12]使用其改进模型,模拟了光滑毛细管和窄喉管道中的气泡-水流动,系统分析了煤的润湿性对切割两相流动的影响．Sankaranarayanan等[13]运用多组分伪势LB方法建立了气泡流动的LB基准模型,成功模拟了单个气泡和规则气泡群的上升过程,其结果与实验数据一致．Yuan和Schaefer[14]将伪势模型推广到大密度比的情况,但应用于动态问题时会受到限制．部分研究者也尝试建立基于相场理论的LB模型[15-16],该模型可以很好地进行界面捕捉,在多相流模拟计算中越来越流行[17]．Lou等[18]基于大密度比LB模型,对气泡在不同类型多孔介质中的上升过程进行数值模拟,研究了不同Eotvos数、黏度比、孔隙形状、气泡数量及不同多孔介质排列方式下的气泡和流体动力学．

以上研究揭示了气泡在复杂结构微通道内的运动机理,但主要集中于气泡通过自身浮力竖直上升方面,对水平通道内受液相强制流动下驱动的气泡运动行为关注较少,而此类两相流动问题在工程应用中十分常见(如潜艇水下排气系统水平通入废气进行降温降噪)．本文使用Liang等[19]提出的基于Allen-Cahn方程的相场LB模型,对受液体推动的气泡在含孔板结构的水平微通道内的运动形态进行了模拟研究;通过考察气泡变形、分裂、合并、质量损失和速度变化等动力学行为,分析了不同气泡状态参数和表面润湿性对气泡穿过孔板过程及其后续演化的影响．

1 数 值 方 法

在气液两相流动的数值计算中,两相界面的捕捉计算是一个复杂的问题,为准确描述整个流体系统中多种非混溶流体共存的状态以及它们在相互作用下的运动,相场模型将任意位置上非混溶流体所占的体积分数定义为该点的序参数,气液相界面由一个连续的薄层表示．

Liang等[19]提出的相场LB模型采用两个分布函数分别用于捕获相界面和描述速度/压力场,其中序参数分布函数满足保守Allen-Cahn方程,如下所示：

(1)

式中,φ为序参数,φ取0和1分别表示气相和液相,当0<φ<1时为气液间界面;M为迁移系数;t表示时间;n=∇φ/|∇φ|,n是垂直于界面单位向量;λ为序参数φ的函数,

(2)

式中,W为界面厚度．

流体运动速度u和压力p等宏观量还需满足不可压缩的Navier-Stokes方程．对于Allen-Cahn方程和Navier-Stokes方程,具有BGK碰撞算子的LB演化过程可分别表示为

(3)

(4)

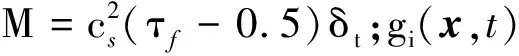
在两相流系统中,由于存在不同物质,流体动力黏度μ并非定值,动力黏度由序参数和气液两相各自的动力黏度线性差值得到,计算公式如下：

μ=φ(μl-μg)+μg．

(5)

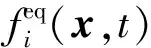
(6)

(7)

(8)

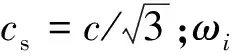
(9)

在式(3)、(4)中,外力项Gi(x,t)和Fi(x,t)的计算公式如下：

(10)

(11)

其中偏导项∂t(φu)可由显式Euler法计算：

(12)

为描述气泡与黏性液体的相互作用,力项F由表面张力Fs与外力Fg相加而得,Fs=μφ∇φ,μφ=4βφ(φ-1)(φ-0.5)-κ∇2φ是化学势．式中,κ和β是常数,由界面厚度W和表面张力σ决定,即κ=1.5σW,β=12σ/W．

通过对分布函数求和,可以得到序参数、压力和速度等宏观统计量：

(13)

(14)

(15)

数值迭代中,对模型内导数项进行差分离散,梯度项和Laplace算子采用二阶各向同性中心格式计算：

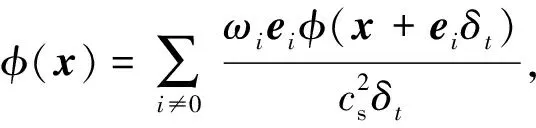
(16)

(17)

其中,离散速度ei的表达式为

(18)

式中,c为格子速度,计算方式为c=δx/δt,δx和δt分别表示格子长度和格子时间,本文中取δx=δt=1．

而对流固界面处的润湿性参数,本文采取虚拟密度法进行构建[20],以微通道底部边界为例,对于固体边界处的格点,虚拟节点上的序参数计算式如下：

(19)

其中导数项采用二阶中心差分法计算：

(20)

2 物 理 模 型

本文所研究水平管道的几何模型如图1所示,在计算域为Nx×Ny=840×120的微通道内,包含一块垂直放置的孔板结构,孔板的左表面距离计算区域左边界Lqx=360,孔板厚度wd=15,孔板的开孔半径rd=6,板上四个开孔的中心位置纵向坐标分别为15,45,75,105．

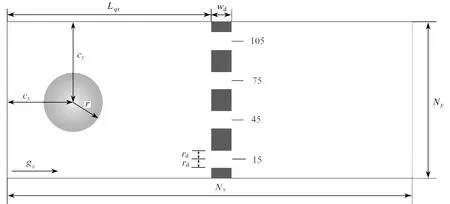
图1 模型示意图

初始时刻,在孔板前方放置一个半径为r,动力黏度μg=1的圆形气泡,其圆心距计算区域左沿距离cx=60,距计算区域上沿距离cy=60,周围区域为动力黏度μl=100的液相流体．气相密度ρg设置为1.0,液相密度ρl为1 000,其他参数固定为界面厚度W=4.0,迁移率M=0.1．气泡在水平管道流动的体积力推动下(体积力Fg=gx×ρ)经过孔板并流出计算区域．本文并未考虑竖直方向的浮力．对微通道的上下壁面采用半步反弹边界,左右边界采用周期边界．如无特殊说明,文中所涉及的仿真参数和计算结果均为格子单位．

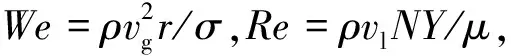
3 模 型 验 证

3．1 Laplace验证

与其他研究一样,本文首先使用Laplace定律验证了模型对于气液分离的正确性．Laplace定律表明,对处于稳定状态的气泡,气泡的内外压差ΔP与气泡半径r的倒数呈线性关系,即满足以下关系式：

ΔP=|Pin-Pout|=σ/r,

(21)

式中,Pin为气泡内部流场的平均压力,Pout为气泡外部流场的平均压力．

设置计算区域Nx×Ny=200×200,四周均采用周期边界．液相和气相密度分别为ρl=1 000和ρg=1．在初始时刻,计算区域被液相填充,一个圆形气泡被置于区域中心,通过改变气泡半径大小得到不同压差．半径分别选取r=15,20,25,30,35,并分别在三种不同表面张力σ=0.1,0.2,0.3下进行模拟．如图2所示,数值结果与式(21)吻合较好,ΔP与1/r呈线性关系,符合Laplace定律．

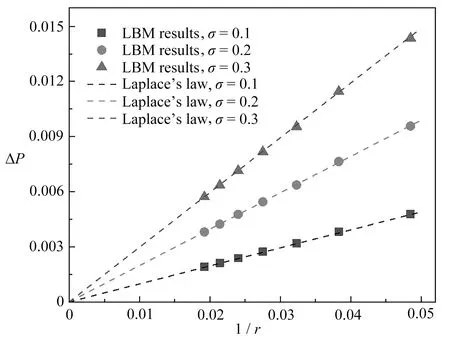
图2 Laplace验证

3．2 润湿性验证

为了验证当前润湿边界方案在实现非稳态运动过程中接触角方面的能力,本小节以毛细管的侵入为典型润湿现象进行模拟．在尺寸为L×H=400×20的毛细管中,初始时刻由未润湿性气体填充,然后外部润湿性液体侵入管内．总计算区域设为Lx×Ly=800×36,其中毛细管占据区域为200≤x≤600,气体组分的位置为240≤x≤750．液气密度比为ρl/ρg=1 000,黏度比设置为μl/μg=100(其中μl=100,μg=1)．其他参数取σ=0.2,M=0.1,W=4．对所有管壁施加无滑移边界条件,对毛细管管壁边界采用润湿性边界方案,其余边界设置为周期边界．如果忽略重力和惯性效应,相界面的演化可以描述为

(22)

如图3所示,本小节计算了在三种不同的规定接触角θ=30°, 45°和60°下,使用润湿边界方案模拟得到的毛细管侵入距离和公式计算结果的比较．需要注意,由于式(22)中未考虑惯性效应、初始条件以及进气道效应等因素,本模型数值结果会小于式(22)的计算结果．且随着接触角的增加,由σcosθ决定的毛细管力减小,在较大接触角下,二者之间的偏差还会增大．图3中还将本文模拟的毛细管的侵入距离与采用类似润湿性方法的模拟结果[20]进行对比,两者最终结果在三个不同接触角下的偏差分别为1.5%,0.9%,0.4%,故可认为该润湿性方法是有效的．

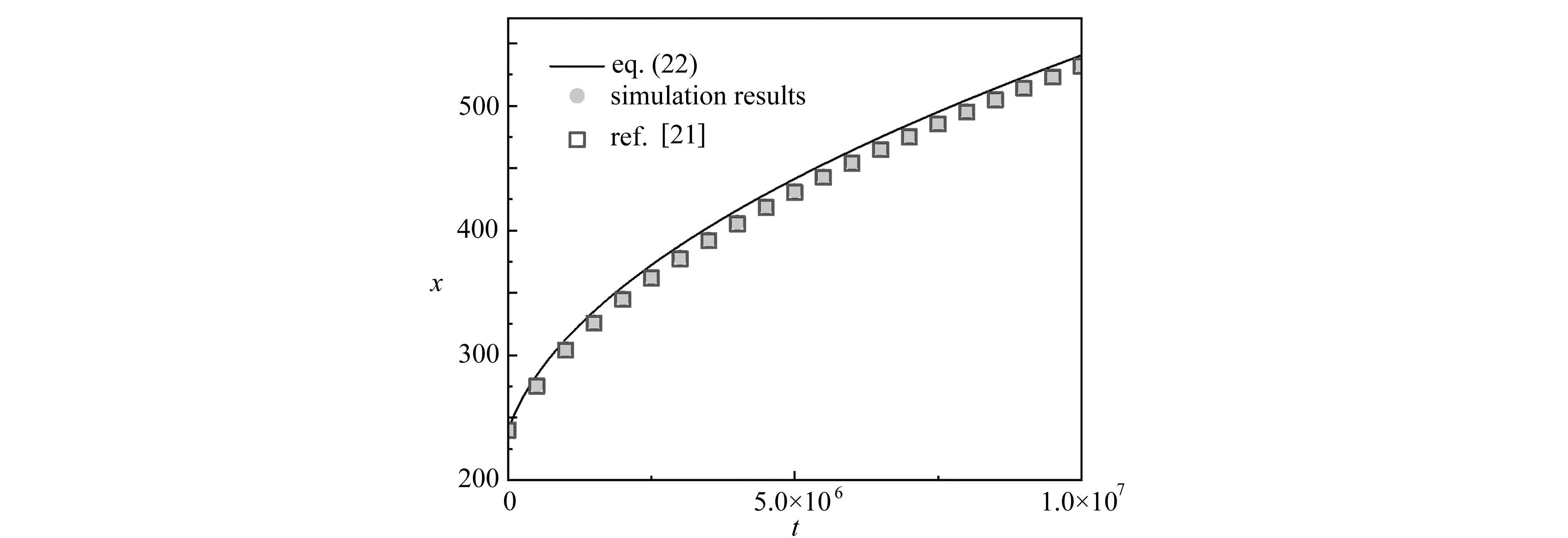
(a) θ=30°

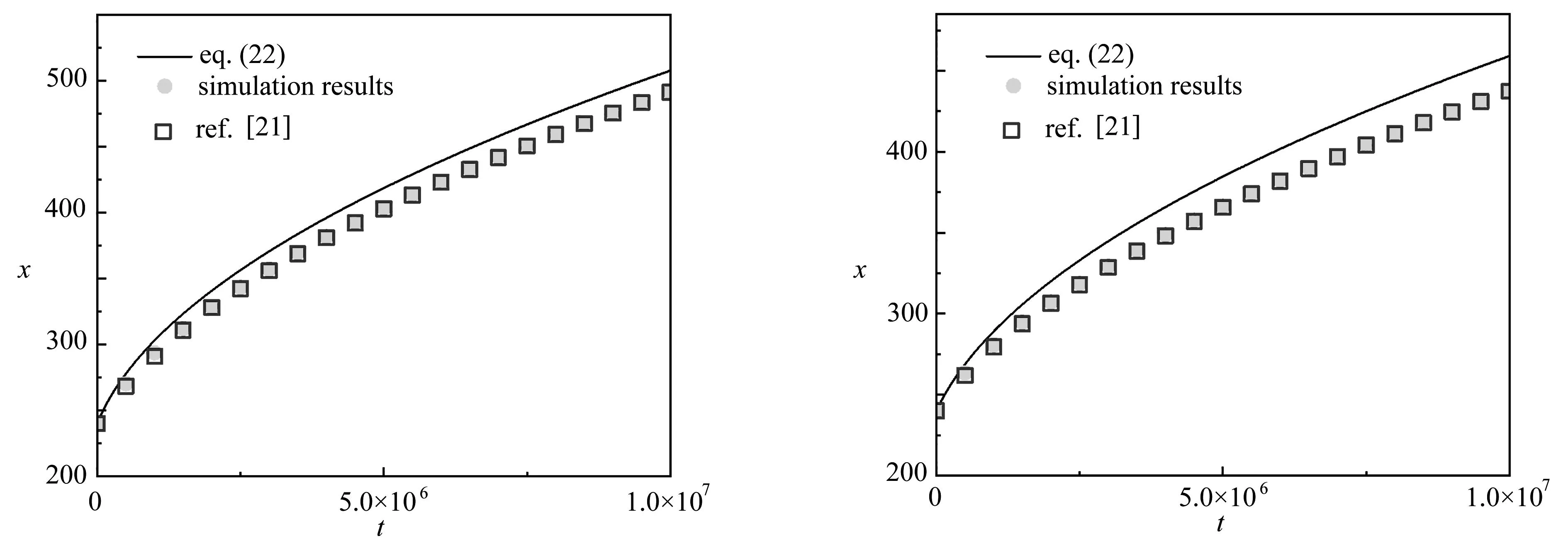
(b) θ=45°(c) θ=60°图3 润湿边界对毛细管侵入的模拟图

3．3 网格独立性验证

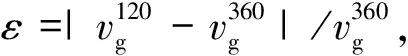
图4给出了在四个不同密度的网格下,气泡在进入及离开孔板时,其界面轮廓的局部图．可以看出Nx×Ny=840×120和1 120×160网格得到的气泡轮廓几乎相同．而由图5显示,气泡通过孔板时,随着网格密度的增大,气泡的气体平均速度vg和通过孔板时间t*的相对偏差ε逐渐减小,并且在Nx×Ny=840×120和1 120×160两种网格密度下与密集网格的相对偏差ε均小于1%,这样的偏差是可以接受的．综合考虑计算精确度需要和运算成本,本文采用840×120网格进行计算．

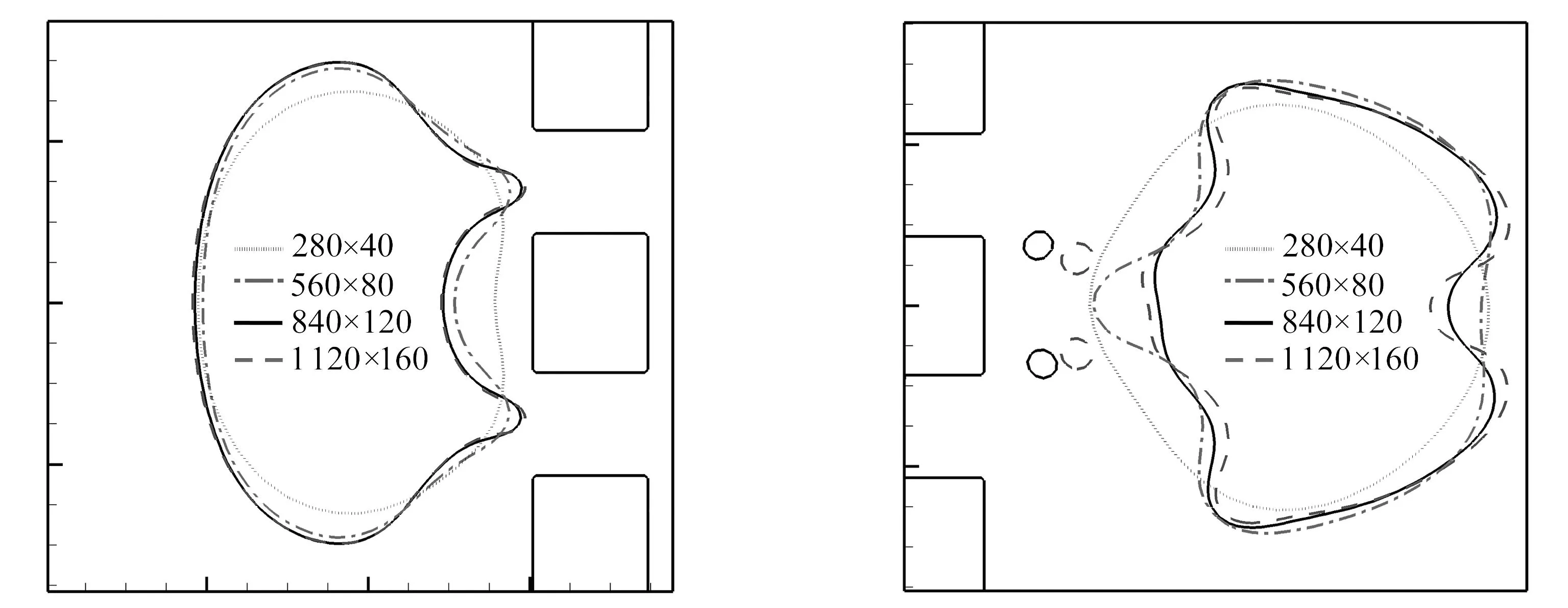
图4 气泡进入孔板和离开孔板时,不同网格下的气泡轮廓

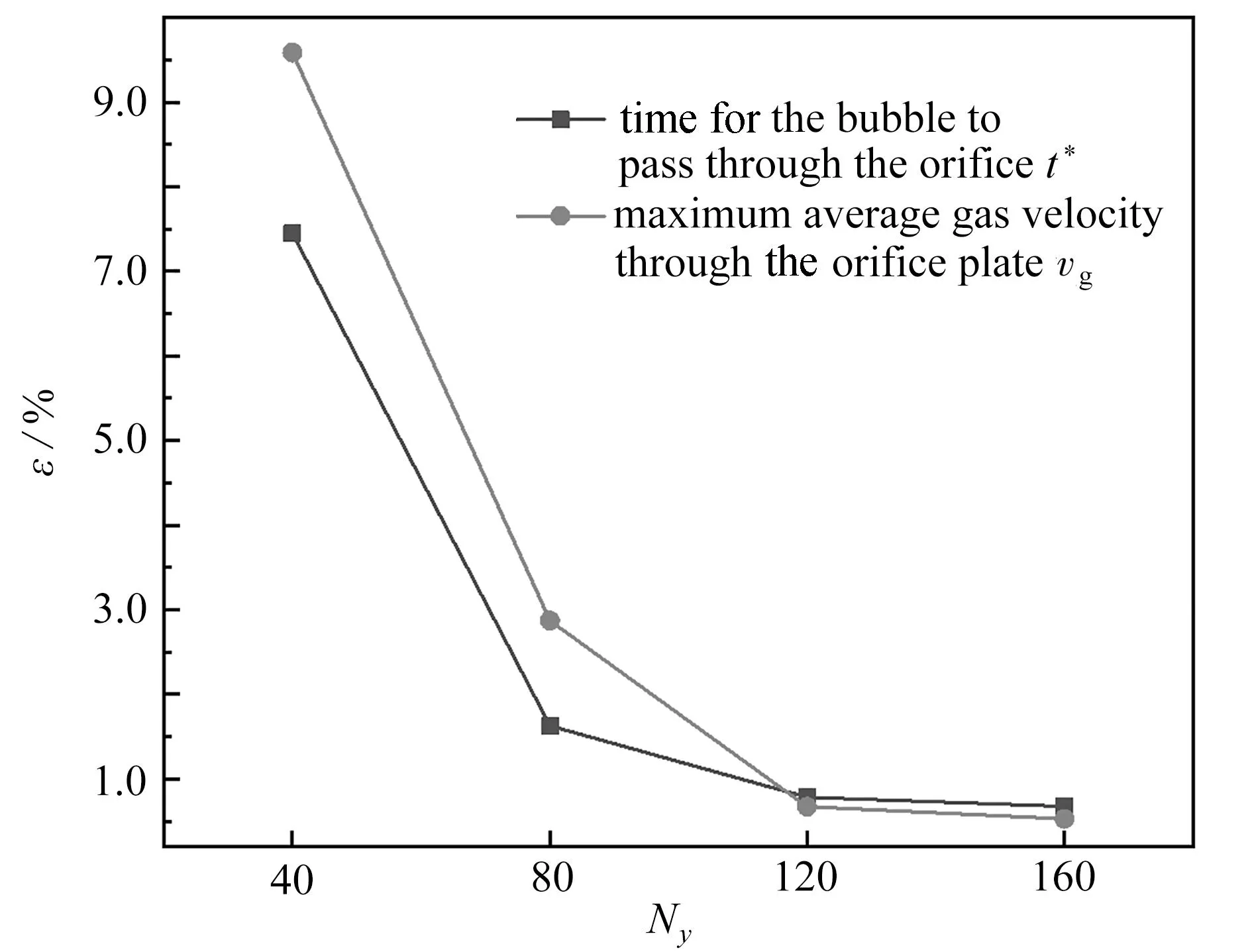
图5 网格独立性验证

4 计算结果与分析

4．1 We数对气泡通过孔板的影响

气泡在液体中的变形和破碎主要受外力和表面张力之比的影响,这一关系可以用We数进行描述,本小节主要讨论不同We数下气泡在水平管道的运动及撞击孔板表面的动态过程．

图6为不同We数(We=0.588,1.176,4.704)下气泡通过孔板的动态过程,此时Re=4.38,气泡半径r为32个格子单位．可以看出, 随着We数的增加, 气泡在通过孔板时呈现出不同的形态．如图6(a)所示,We=0.588时,气泡在孔板结构前受到连续流体推动向前运动,在表面张力和黏性力作用下逐渐达到稳定,呈现“子弹形”．当气泡逐渐向右运动并接近孔板时,气泡受中间障碍产生的两个前缘呈现曲率半径呈减小趋势,当前缘到达孔板位置时达到最小值．然后,随着前缘穿过孔喉,其曲率半径回升增大,这一趋势与实验中气泡穿过孔隙结构的现象相吻合[21]．由于孔板部分管道宽度快速变窄,气泡平均速度剧烈上升,留在孔板前端的“尾部”气膜变薄,气泡受到强烈的黏性切断力[7]产生变形和破裂．由于气泡内部存在对称的黏性应力,气泡破裂为两个大小几乎相同的子气泡．受孔板后方回流影响,破裂子气泡在通过孔板后速度随即下降,快速互相靠近发生二次聚合．聚合形成的新气泡在表面张力作用下,排出内部小液滴逐渐恢复稳定,再度发展至子弹形．如图6(b)所示,在We=1.176工况下,气泡表面张力减小,故在运动过程中形成子弹形后,会继续发展为“弹弓形”,处在管道中间气膜的厚度减小而两侧体积增大．因此,当气泡在通过孔板结构时,部分气体会从靠近管道壁面的开孔通过,整体被分割为四个主要子气泡．中间两个子气泡如同刚才一样重新汇聚后发展为稍小的子弹形气泡,由于破碎后结构的不对称性,很多情况下该破碎气泡会被流动推向管道一侧(t*> 3.5时)．靠近两侧的子气泡由于速度差距较大而独立发展,形成扁平状气泡并在靠近壁面的位置运动．继续增大We数,如图6(c)所示,当We=4.704时,由于表面张力进一步缩小,气泡在运动到孔板之前已经产生巨大形变,直接被液体流动完全分解(t*=1.991),大部分残余气体被挤压到两侧的低速流动区,在通过孔板时被进一步撕裂,在管道两侧形成连续的扁平泡状流．而“头部”的少量气体在通过孔板后重新汇集成箭头形向前流动,运动速度远高于两侧的分裂气泡．

(a) We=0.588 (b) We=1.176 (c) We=4.704图6 d/D=0.533 33的气泡通过孔板的动态行为

从图7的气体与液体流速随时间变化图可以观察到,气泡在低We数下通过孔板是一个连续过程,气体与液体速度存在一个共同的波峰．随着We数的增加,气泡变形程度提高,部分被分割的子气泡在孔板靠外的位置通过,从而使气体平均速度产生了两个存在时间错位的峰值．由于中部汇聚气泡在一段时间后被推离管道中心,气体平均速度在后续时间(t*> 3.5时)相比通过孔板前会更低．而We数更高时,气泡经过前孔板已经被撕裂,但位于管道中部的“头部”残余子气泡也因此有了更高的速度,气泡的“头部”部分更早运动到孔板位置后流过,使气体与液体流动速度均有提前的小幅加速．而两侧气泡偏向长条的形状,使孔板结构持续会有小型子气泡分解流过,故气液平均速度提高的时间会持续得比之前两种情况更久．

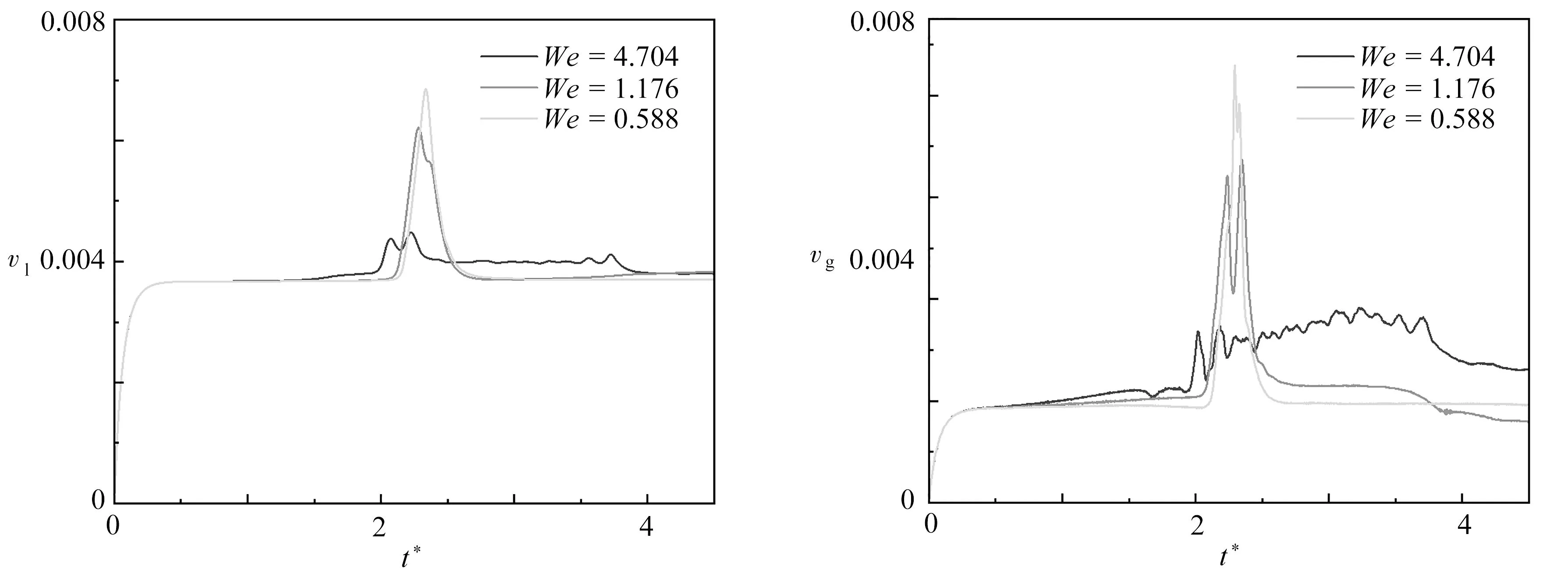
(a) 液体速度 (b) 气体速度(a) The liquid velocity (b) The gas velocity图7 气液速度随无量纲时间t*的变化

4．2 直径比对气泡融合和脱落过程的影响

本小节讨论在Re=4.38条件下,气泡大小对其通过横向管道孔板的影响．为方便参考,选择气泡直径与管道直径之比d/D为气泡大小的参照．在模拟中分别设置了d=0.266 7D至d=0.533 3D等多种不同大小的气泡．

图8给出了在不同直径比d/D和We数下,气泡流经孔板的相图．不同气泡在通过孔板时,会表现出三种形态：先分裂再聚合、直接分裂和先撕裂再分裂．在直径比d/D和We数均较小时,气泡主体会在被孔板分裂为两部分后再次聚合为一个气泡运动．当气泡处于较高We数时,其直径比d/D会出现两个临界值．当d/D大于第一个临界值而小于第二个临界值时,气泡会被孔板分裂为三个主要子气泡运动,而当d/D超过了第二个临界值时,气泡将在孔板前直接被流动撕裂,并被孔板进一步分裂为众多小气泡．这两个临界直径比的大小都会随着We数的增加而降低．

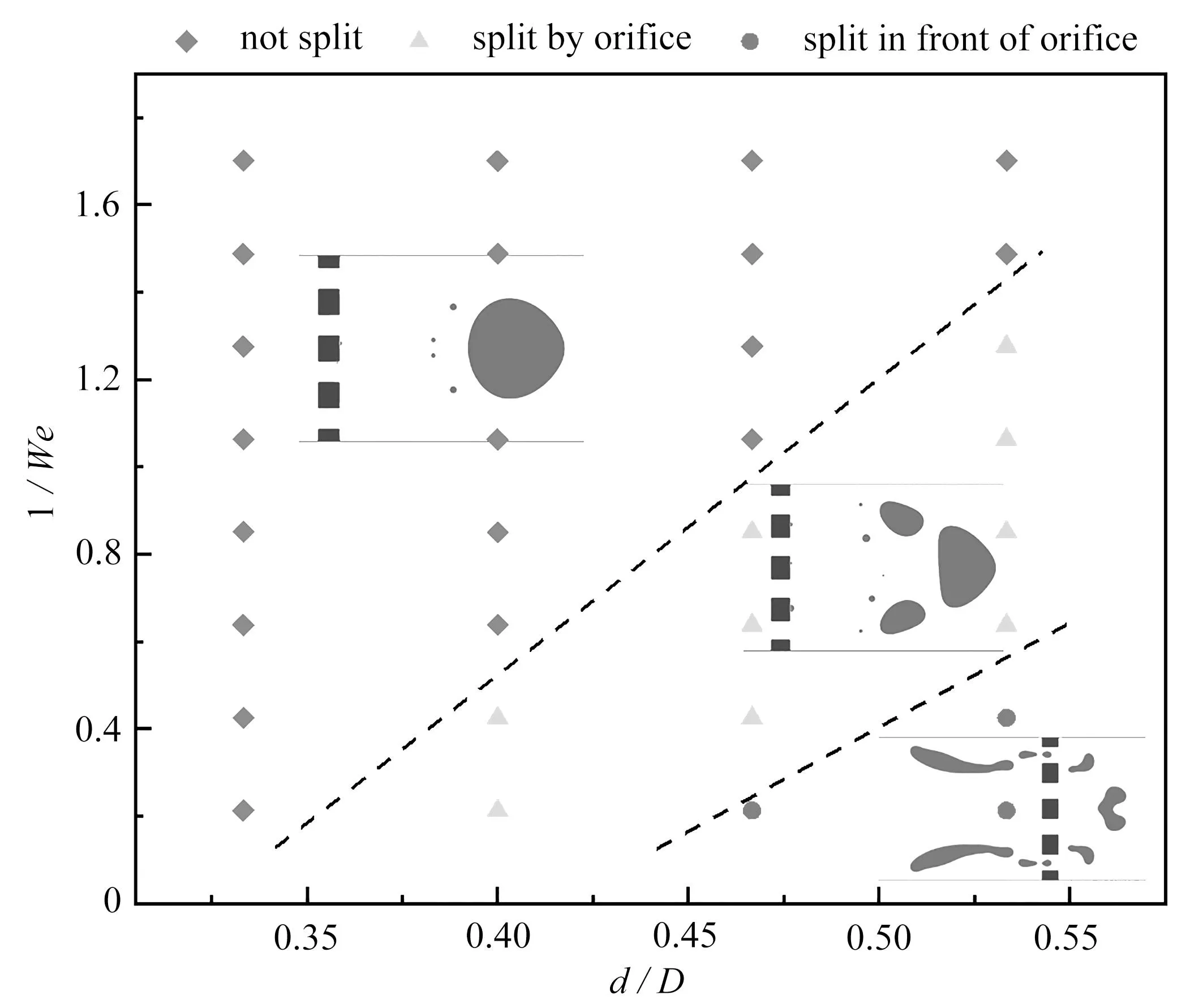
图8 不同1/We和d/D下气泡通过孔板的动态行为

4．3 润湿性影响

孔板孔喉部分毛细压力受表面润湿性的影响,会改变非润湿相通过孔喉的能力．本小节为研究孔板表面润湿性对水平微通道内气泡-水流动特性的影响,分别对不同接触角情况进行了一系列数值模拟,包括θ=30°,60°,90°,120°,150°．气泡参数如下：d/D=0.4,Re=4.28,W=4.0．

其中三种不同接触角下气泡的运动过程如图10所示,孔板表面润湿性变化对气泡在横向微通道内的动态行为存在较大影响．如图10(a)所示,当θ=60°时,孔板表面处在疏气亲水工况,在横向驱动力、表面张力和孔板表面阻力等共同作用下,气泡前端进入孔板之中并与孔板表面发生接触．之后,气泡以极快速度通过孔板,在加速和减速过程中受到孔板表面阻力和表面张力的共同作用,有小部分气体被撕裂独立发展(t*=2.756 3),主体气泡重新恢复为子弹状(t*=3.368 8)．

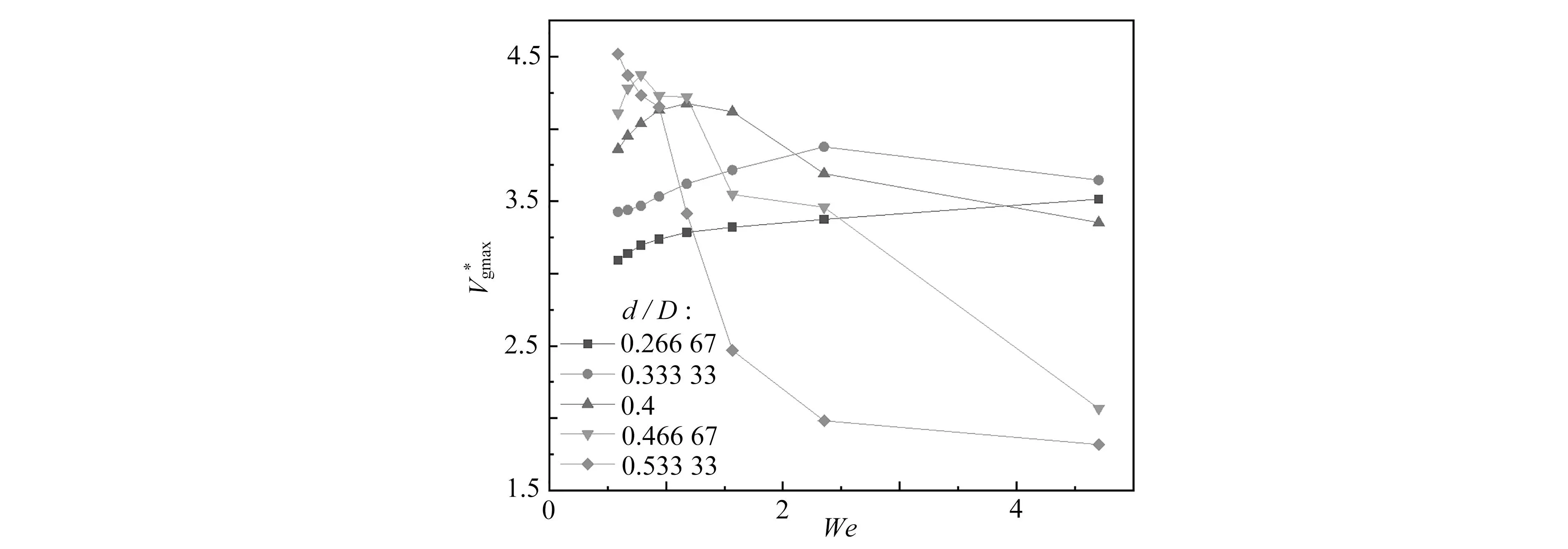
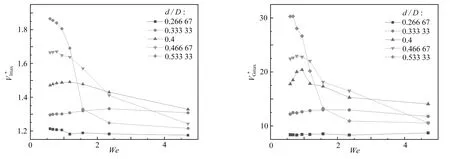
图9 气泡运动过程中在不同d/D下几种运动参数随We数的变化

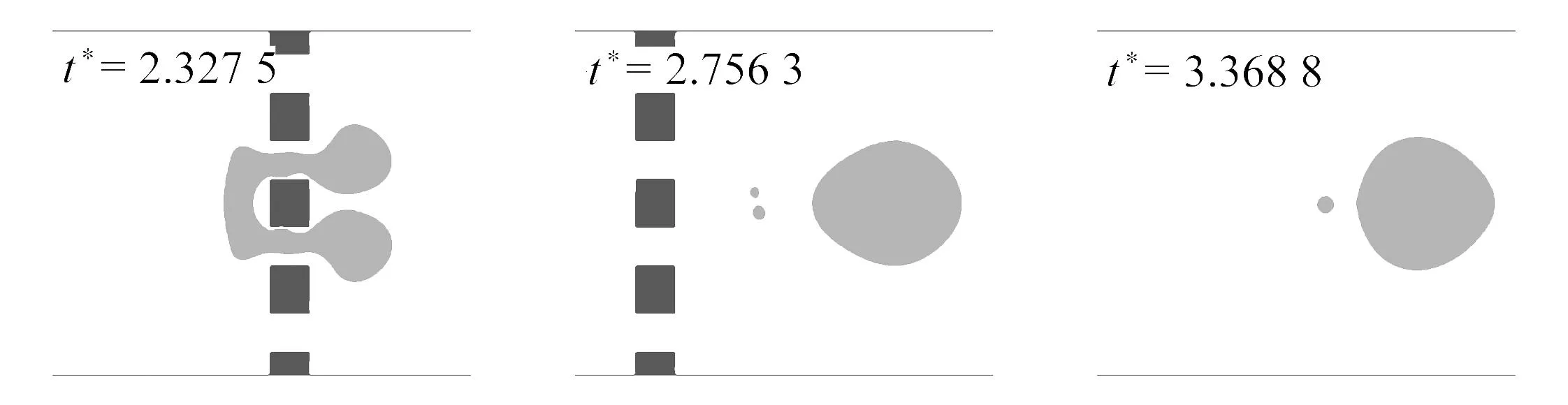
(a) θ=60°

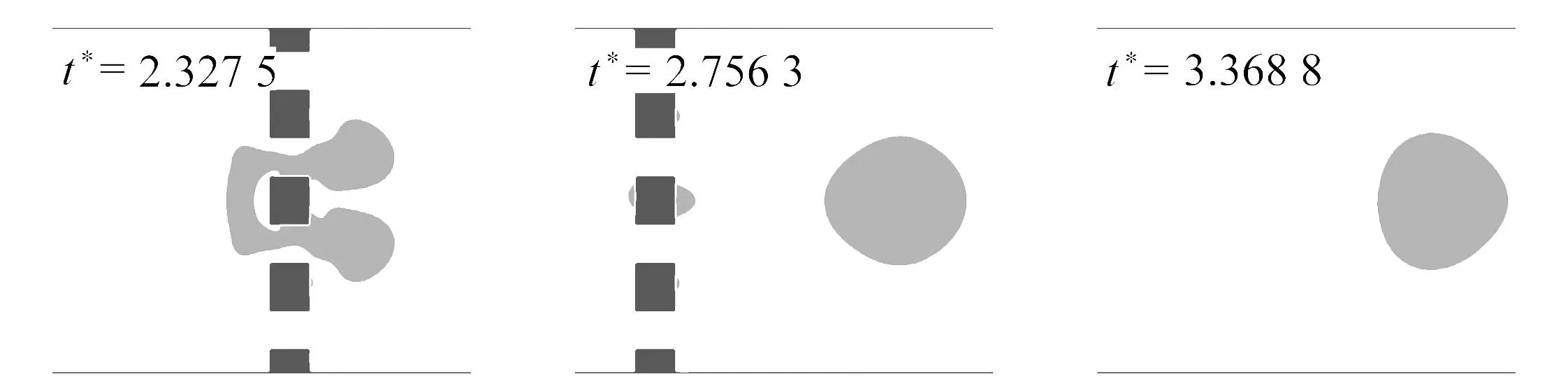
(b) θ=120°

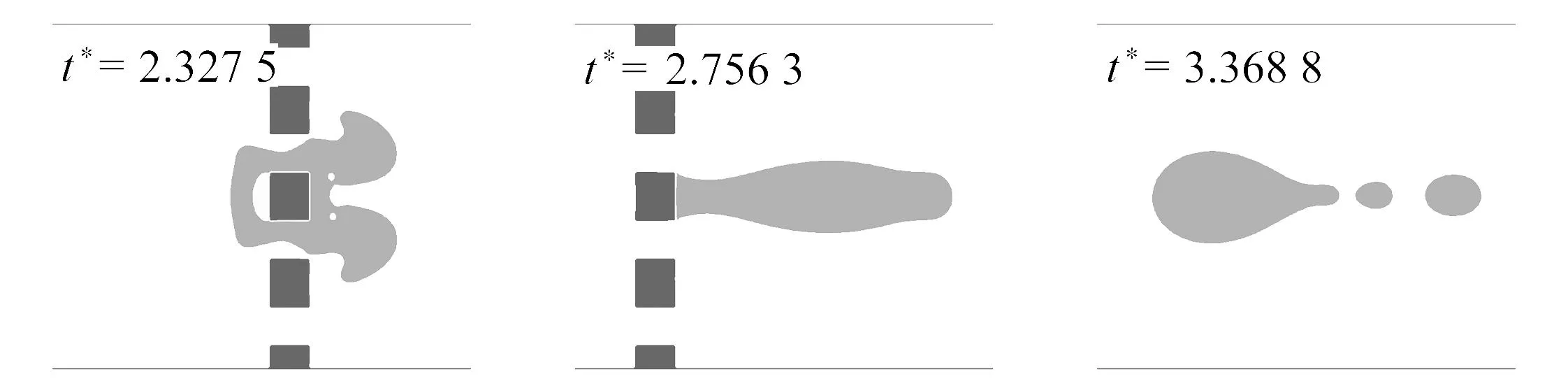
(c) θ=150°图10 气泡通过不同润湿性孔板动态行为

当接触角θ=120°时,如图10(b)所示,相比于θ=60°工况,由于孔板障碍表面亲水性减弱,导致气泡在通过孔板过程中与表面的接触面积增大．在通过孔板结构的速度变化过程中,气泡同样出现了破裂现象,但在亲气表面产生的破碎小气泡会倾向于黏在孔板后方(t*=2.756 3)．主气泡与亲水工况一样演化为子弹形状(t*=3.368 8)．如图10(c)所示,随着孔板表面亲气性进一步加强,接触角增大为θ=150°,气泡几乎紧贴着孔板表面穿过孔喉(t*=2.327 5),受到结构表面毛细力影响,气泡会整体被孔板结构捕获,被捕获后的气泡滞留在孔板结构后方(t*=2.753 6)．气泡前端会产生两个先行分离的小气泡,气泡的主体随后在液流驱动下离开孔板,继续发展演化．

(a) εg

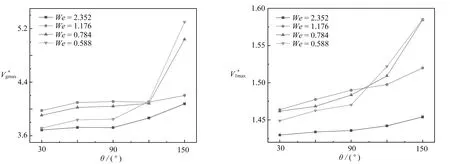
图11 气泡运动参数随孔板润湿性变化

为定量分析孔板润湿性改变对气泡运动的影响,本文统计了不同接触角下不同We数气泡的运动数据和残余质量εg．气泡残余率如图11(a)所示,当孔板表面亲气性较弱时,气泡不会被结构吸附,几乎可以整体穿过孔板(θ=30°,60°)．当θ>60°后,随着表面亲气性的加强,气泡残余质量逐渐减小,但整体质量损失不大(均小于10%)．观察图11(b)不难发现,当θ=60°,90°,120°,150°时,气泡的最大平均速度比分别为3.92,3.93,4.04,4.65(不同We数的气泡取平均),即当孔板表面开始成为亲气表面时,接触角以相同幅度增大,但气泡运动中的最大平均速度分别提高了0.3%,2.8%和15.2%．因此随着接触角的增大,通过孔板结构的平均气泡速度也逐渐增大,此外当接触角大于120°后,平均最大气泡速度随着接触角增大的程度更加剧烈,特别对We数较低的气泡尤为明显．图11(c)显示,在接触角增大的过程中,周围液体的最大平均速度也出现了和气体速度类似的现象,不过在大接触角下的增加程度没有气体速度显著．

5 结 语

本文基于Allen-Cahn方程的大密度比相场LB模型,对气泡在含孔板微通道内的运动过程进行了数值模拟研究．分别考虑了We数、气泡当量直径和孔板表面润湿性等因素对气泡平均速度和破碎性等运动学特性的影响,得到了如下结论：

1) 随着We数的增大,气泡在孔板前的形变会更加剧烈,表现为气泡边缘到两侧管壁的距离逐渐缩短,气泡在通过孔板时更容易发生破裂、汇聚等形变;气泡通过孔板过程中,当气泡大小和流动强度均相同时,We数的增大会使速度变化的时间更长．

2) 在本文所研究的参数范围内存在两个临界直径比,这两个临界直径比将气泡通过孔板的运动分成了“分裂后聚合为一个气泡”“被孔板分裂”和“在孔板前被撕裂”三种形态．而气泡直径比d/D的增加会使得气泡运动过程中出现最高速度时所需要的We数逐渐变小,最高气泡速度、单点速度和液体速度峰值则会随之增加．

3) 随着接触角的增大,孔板结构亲气性越强,孔板表面对气泡的吸附作用越明显．此时气泡与孔板的接触面积增大,被吸附的气体也越多,导致穿过孔板的气泡体积逐渐减少．且随着接触角的增大,气泡的最大平均速度增加,气泡通过孔板的时间减少,这在接触角大于120°后尤为明显．

实际微通道中的气泡运动是一个三维问题,本文采取二维模型计算,后续应通过优化并行效率计算三维情况,使结果更符合真实情况,尤其是对于计算含浮力水平通道内流动的问题[22]．我们希望这一数值研究有助于理解气泡动力学的基本物理原理,以及在未来的微结构流体应用中设计更为接近现实的复杂流动．