考虑Gauss移动热源瞬态效应的传热结构拓扑优化
周崇伟, 赵清海,2, 陈建良, 时高松
(1. 青岛大学 机电工程学院, 山东 青岛 266071;2. 青岛大学 电动汽车智能化动力集成技术国家地方联合工程研究中心, 山东 青岛 266071)
0 引 言
移动热源散热问题在工程应用中普遍存在,如汽车制动盘摩擦生热和金属材料的热处理等.考虑移动热源条件下传热结构的瞬态热效应,设计高效散热拓扑结构,将移动热源的热量迅速地传递到环境中,从而有效提高结构的散热性能,具有重要研究意义.
Caroline[1]分析了移动热源在半无限大物体中引起的热传导问题,无限时移动热源周围的温度场表现为稳态.Atluri等[2]考虑热传导系数因素,在较宽的热源速度范围内研究了运动热源所产生的温度场,给出了不同坐标系中,不同速度情况下,温度场随时间变化的情形,并给出了不同热源速度下的温度场分布.对于稳态热传导问题,左孔天等[3]通过对热传导结构进行数学建模,设计出结构优化的最佳散热路径.Bouk[4]对拓扑优化方法系统进行了比较,并对拓扑优化方法在热传导问题中的实际工程应用现状进行了综述.陈拥平等[5]以变密度法为基础,建立了以结构散热弱度最小化为目标的稳态热传导拓扑优化模型.赵清海等[6]提出了一种周期性约束下的稳态热传导拓扑优化设计方法.张晖等[7]针对热源随结构变化的稳态热传导结构优化问题, 考虑热载荷的拓扑相关性进行了优化设计.龙凯等[8]基于独立联系映射法,解决了多工况下的稳态热传导拓扑优化问题.闫浩等[9]提出了一种密度指数函数插值的有序多材料性能近似模型,实现了三类热边界条件下复杂热环境的多材料传热结构拓扑优化.Zhao等[10]基于无网格的广义有限差分法和具有惩罚插值模型的固体各向同性微观结构,提出了稳态散热结构的拓扑优化方法.
上述文献都是基于稳态热传导开展研究的,然而移动热源温度场本质上为瞬态,其温度分布大都随时间和空间变化.因此,Turteltaub[11]将SIMP方法扩展应用到瞬态拓扑优化,考虑了瞬态效应对拓扑优化结果的影响.吴书豪等[12-13]基于区域温度控制函数构建瞬态热传导拓扑优化数学模型,开展了瞬态热传导结构拓扑优化方法研究.李信卿等[14]搭建了基于有序有理近似材料属性法的多材料插值模型,提出了一种周期性多材料瞬态热传导拓扑优化设计方法.Zhuang等[15]对瞬态热传导设计的多重温度准则和三相拓扑优化进行了探究,考虑了瞬态效应的热传导拓扑优化过程中热柔顺度最大值最小化的问题.上述考虑瞬态效应的拓扑优化设计,极大地推动了考虑热源时变下传热结构设计优化理论的发展.
综上可知,散热结构拓扑优化设计缺乏考虑移动热源瞬态效应对拓扑优化结果的影响.考虑移动热源的瞬态效应时,热源随时空变化增加了传热结构优化的复杂性.因此,本文基于瞬态热传导优化设计问题,建立了以变密度法为基础的拓扑优化模型.针对Gauss热源模型进行仿真模拟,分别考虑了以传热结构区域温度最大值最小化与最小散热弱度为设计目标,通过伴随变量法对目标函数与约束条件进行了灵敏度推导,并基于移动渐近线法对设计变量进行了更新迭代.最后通过数值算例验证了所提方法的必要性与有效性.
1 瞬态热传导效应分析
热源的瞬态效应涉及到结构热传导随时间变化,需要建立复杂的瞬态热传导模型.这要求对瞬态热传导过程进行准确建模,包括考虑瞬态热传导方程、边界条件和初始条件等.尤其在移动热源进行传热结构优化时考虑热源瞬态效应,其随时间空间均发生变化.
1.1 考虑瞬态响应的传热结构
考虑瞬态效应的传热结构如图1所示,由热源Q(t)加热的设计域应用了两种边界条件,一个是恒温边界Γ1,另一个是绝热边界Γ2,设计域内部采用高热传导属性的材料填充,设计域需要离散成有限数量的单元,非设计域为低导热系数基板结构.
采用有限元法,温度场的瞬态热传导数学模型可描述为
(1)
式中M和K分别为热容矩阵和热传导矩阵;T为节点温度向量;Q为移动热源的热载荷向量.
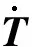
(2)
利用θ-时间差分法[14]求解结构温度和载荷向量:
Ti+θ=θTi+1+(1-θ)Ti,
(3)
Qi+θ=θQi+1+(1-θ)Qi.
(4)
联立式(2)—(4)并代入式(1)中,得到温度场迭代公式:
(M+θΔtK)Ti+1=[M-(1-θ)ΔtK]Ti+Δt[θQi+1+(1-θ)Qi],
(5)
式中θ为算法参数,θ=1时,式中向前差分,θ=0时,式中向后差分;Qi为第i时刻的热载荷向量.
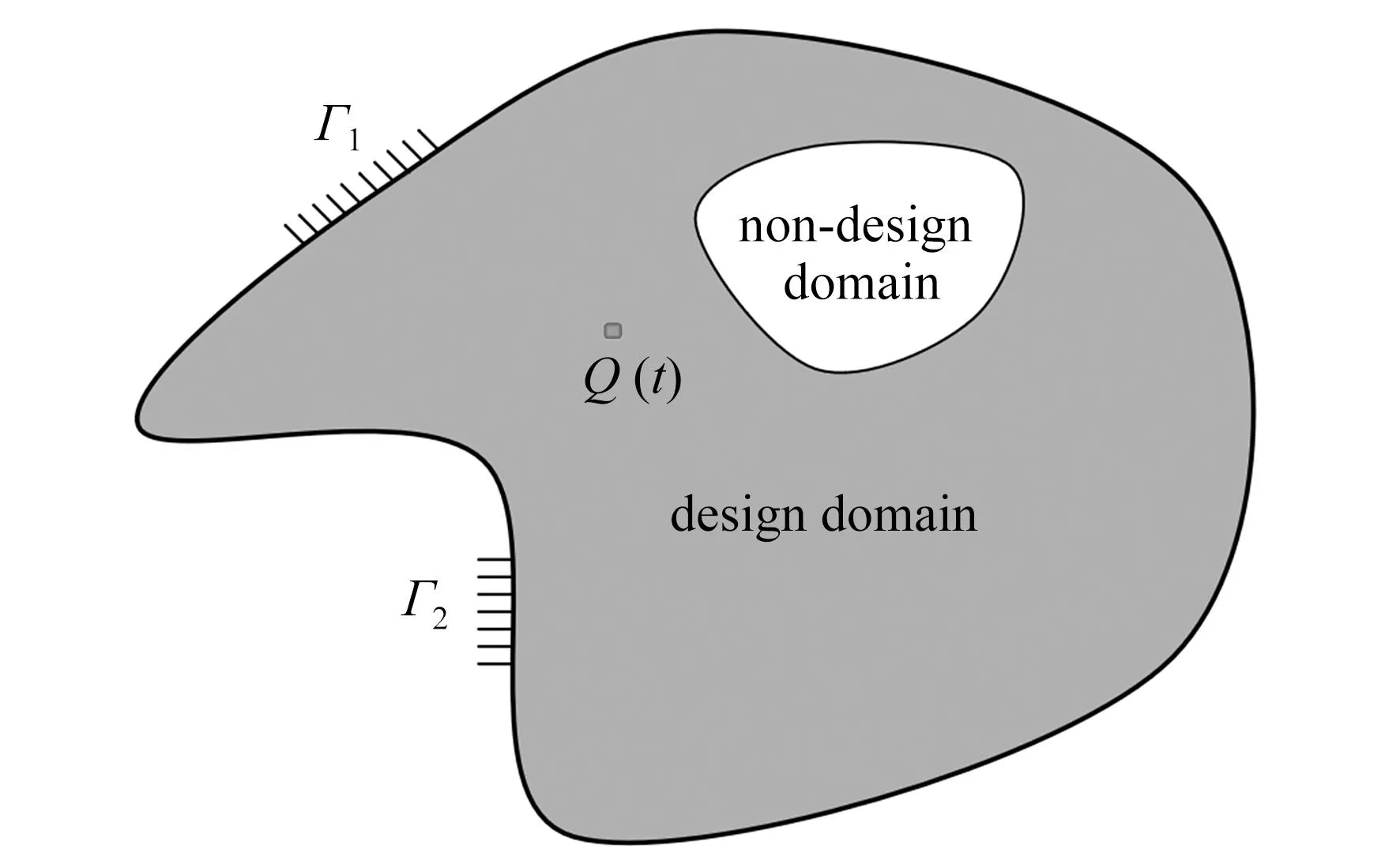
图1 瞬态效应传热材料结构
1.2 热源模型分析
工程中常用的热源模型主要有Gauss热源、Rosenthal的解析热源模型[16]、椭球形热源及多热源组合的复合热源模型.Gauss热源具有中心温度高而周围温度递减的特点,例如制动器摩擦生热及金属热处理等,温度分布符合正态分布,模型如图2所示.

图2 Gauss热源模型
图2中,O为热源中心,R为热源有效加热半径.热源加热过程中任意一点的表面热流密度可确定为
qr=qmaxexp(-μr2/R2),
(6)
式中qr为外部热源有效加热范围内半径为r处的表面热流大小;qmax为加热中心处的最大热流,在Gauss热源有效范围内qmax=103W/m2;μ为热源的集中系数,取值为3.基于有限元思想,将设计域划分为网格状,将Gauss热源施加到单元节点,计算热源作用区域中所有单元节点的热流密度,具体步骤如下:
① 确定热源中心节点的位置.
② 计算单元各节点到热源中心的距离S.
③ 将S与热源有效加热半径R比较,若S不大于R(如图3中OABC四个节点),则按照Gauss模型计算该表面的热流密度;若S大于R(如图3中节点DEFG),则热流密度赋为0.
④ 判断热源在移动过程中满足规律的节点并赋予符合Gauss热源规律的热流密度.
如图3所示,Gauss热源在移动过程中[17],热源作用在基于有限元网格划分后的节点上,相比正态分布的Gauss热源,点热源作用在单个节点上.将移动热源的路径在时间和空间上进行提前规划,使其在单位时间上从指定节点间依次移动.使热源从设计域网格顶点P到达顶点Q,分别设计对角线移动路径以及区域S形移动路径.
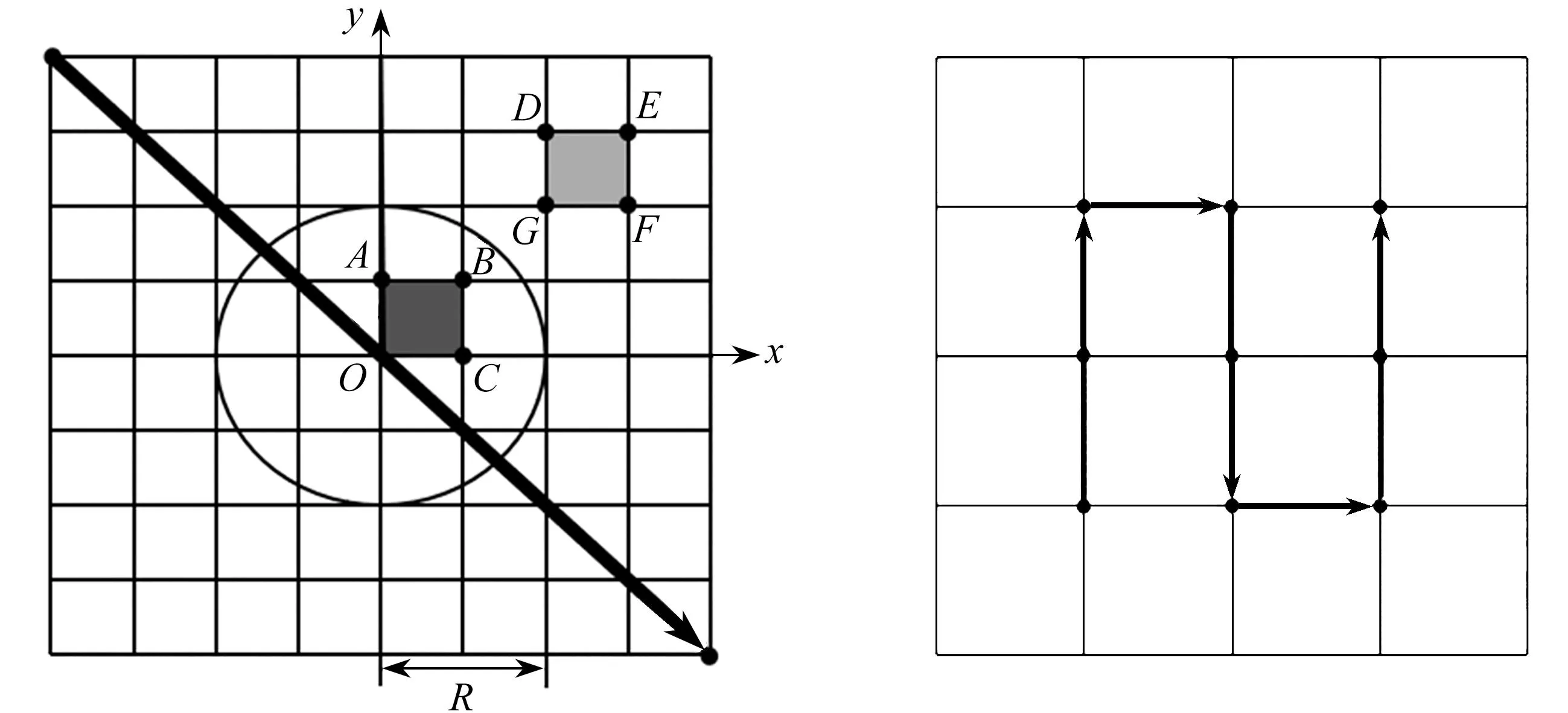
图3 Gauss热源热流密度及模拟路径
经典Rosenthal解析热源模型,其主要被简化为集中热源模型,按照加热材料及尺寸形状等方式将其简化为点状、线状、面状三种热源模式.其热源温度高度集中,如激光加热、焊接等,热源施加在结构表面时,可以将热源看作一个点热源.点热源形成的温度场其解析式为
(7)
式中P为热源所提供的热流量;m为材料热扩散率;l表示到热源点的距离;c为导热介质的比热容;t为热源供热时间.
1.3 Gauss热源仿真
通过对Gauss热源模型移动过程进行仿真[18-19],规划移动路径,观察仿真过程中热源温度分布规律.以顶点为散热边界条件,四周为绝热材料,热源运动模型为
d=v·δt, δt=tf/Nn,
(8)
式中d为移动路径总节点;v为热源移动速度,表示单位时间经过节点的快慢;δt为运动时间步长,它由总时间tf和时间划分段数Nn决定.
令Gauss热源沿对角线以每秒经过一个节点的速度移动,取tf=80,Nn=80.取移动过程中3个位置点观察热源规律,分别取热源在开始、中间位置以及最终位置.
如图4所示,热源匀速缓慢移动过程中符合Gauss分布规律,在初始位置可以明显观察到中间高、四周低的温度分布规律,移动过程中留下明显的“彗尾”状温度,到达终点后,移动路径温度向散热边界方向降低.

图4 Gaussian热源移动过程仿真
1.4 构建瞬态热传导拓扑优化模型
基于变密度[20]理论,考虑移动热源瞬态热传导问题建立优化模型:
(9)
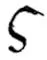
针对目标函数进行分析,考虑如下两种优化目标[22]:
目标Ⅰ 散热弱度
(10)
目标Ⅱ 区域温度
f(T(x,t),x)=LTT(t),
(11)
式中L为列向量,在目标节点处为1,其余为0.
1.5 灵敏度推导
基于伴随变量法求解散热弱度最小化的目标函数.引入Lagrange因子λ1,构建Lagrange函数:
(12)
求解新目标函数的灵敏度,对任意设计变量xn求导:
(13)
将关于温度的偏导数进行分部积分计算,可得
(14)
考虑λ1|tf=0,进行回代,所以上式经过化简为
(15)
忽略载荷设计相关性影响,消除温度灵敏度,则目标函数灵敏度方程为
(16)
(17)
其中,伴随向量λ1计算公式为
(18)
在整个时间历程上以区域内的最高温度最小化为目标,最高温度在瞬态下非连续,导致优化问题的求解变得更加困难,因此用聚合函数φt重新定义最高温度目标函数为
(19)
定义空间函数为
(20)
式中κ为聚合参数,当κ→∞时,φ→Tmax,Ni表示温控区域总节点数量.
结合目标函数与约束条件构建优化准则公式,定义Lagrange函数,ϑt为Lagrange因子:
(21)
目标函数Rt对设计变量xn进行灵敏度推导:
(22)
其中
(23)
(24)
对温度偏导数进行分部积分,考虑ϑt|tf=0同时不考虑载荷设计相关性,消除温度灵敏度项.
忽略热载荷与设计变量关系,目标函数为
(25)
计算Lagrange因子:
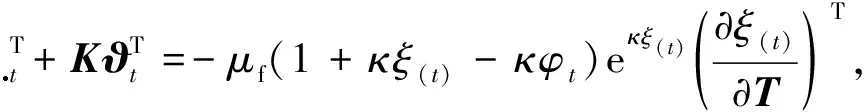
(26)
其中
(27)
(28)
1.6 算法求解过程
考虑瞬态热传导响应,基于SIMP材料插值模型,分析移动热源结构拓扑优化设计研究,具体流程如下:
① 定义散热结构设计区域、材料属性、边界条件、热载荷工作时间.
② 初始化材料设计变量值、温度边界和热负荷移动路径,将设计域进行离散网格划分,获得单元热容矩阵和热传导矩阵.
③ 计算整体热容矩阵和热传导矩阵,利用向前差分法得到温度场和载荷向量.
④ 计算两个目标函数对于设计变量的导数,得到灵敏度并进行灵敏度过滤.
⑤ 利用移动渐进线法对设计变量进行更新.
⑥ 判断优化设计结果是否收敛,若收敛,则输出拓扑构型;否则返回步骤③,重复步骤,直至满足收敛.
2 数 值 算 例
考虑Gauss移动热源在结构中瞬态热传导的问题,针对不同Gauss热源移动路径,给出数值算例.定义传热结构背景区域的热传导系数λmin与热容系数γmin分别为0.2 W/(m·K),2.25 J/(K·m3);在结构区域中施加热源并布置高热传导材料,导热系数为500 W/(m·K),热容系数为1.2×105J/(K·m3).
2.1 对角线路径算例
如图5所示的结构优化设计域,设计域选取为0.1 mm×0.1 mm×0.05 mm的正方形结构,并将其离散成50×50个平面四边形单元.Gauss热源中心点强度为103W,在固定热源设计域中,热源位于设计域的中心位置,四顶点为0 ℃点,四边是绝热边界,在不同加热时间为0.1 s,0.5 s,1 s,5 s和10 s下,研究热传导瞬态效应对结构散热拓扑优化的影响规律.
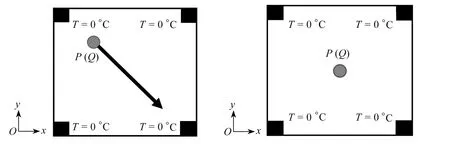
(a) 对角线路径设计域 (b) 中心固定热源设计域 (a) The diagonal path design domain (b) The center fixed heat source design domain图5 结构优化设计域
移动热源沿对角线从左上顶点移动至右下顶点,设计域的余下顶点温度恒为0 ℃,其他边界为绝热材料,过滤半径选取rmin=1.2.
图6中,基于稳态传热的拓扑优化模型只考虑热量传递,忽略了设计域温度不断被上升的情况.随着加热时间不断增加,结构整体温度场并非呈现稳态不变,其温度在逐渐升高,同时拓扑构型受热源瞬态效应的影响变化明显.当加热时间足够大时,考虑瞬态热传导的传热结构拓扑构型趋向于稳态热传导拓扑结果.

图6 稳态热传导与瞬态热传导的拓扑优化结果
针对不同的优化目标(目标Ⅰ为散热弱度,目标Ⅱ为区域温度)对传热结构进行优化.作为对比,将集中热源模型与Gauss热源使其沿对角线路径移动,传热结构优化结果列于表1.
考虑移动集中热源和Gauss移动热源所优化的拓扑结果沿其对角线路径对称分布,且不同优化目标所优化的散热结构材料分布有明显不同.集中热源其拓扑构型受其移动路径的影响,分布更加集中,而Gauss热源热传导路径效果更加明显.
控制Gauss移动热源加热时间,以热源移动速度v为变量,观察传热结构拓扑构型,可以清楚得到其运动过程中受到瞬态热传导影响的变化规律,如图7所示.
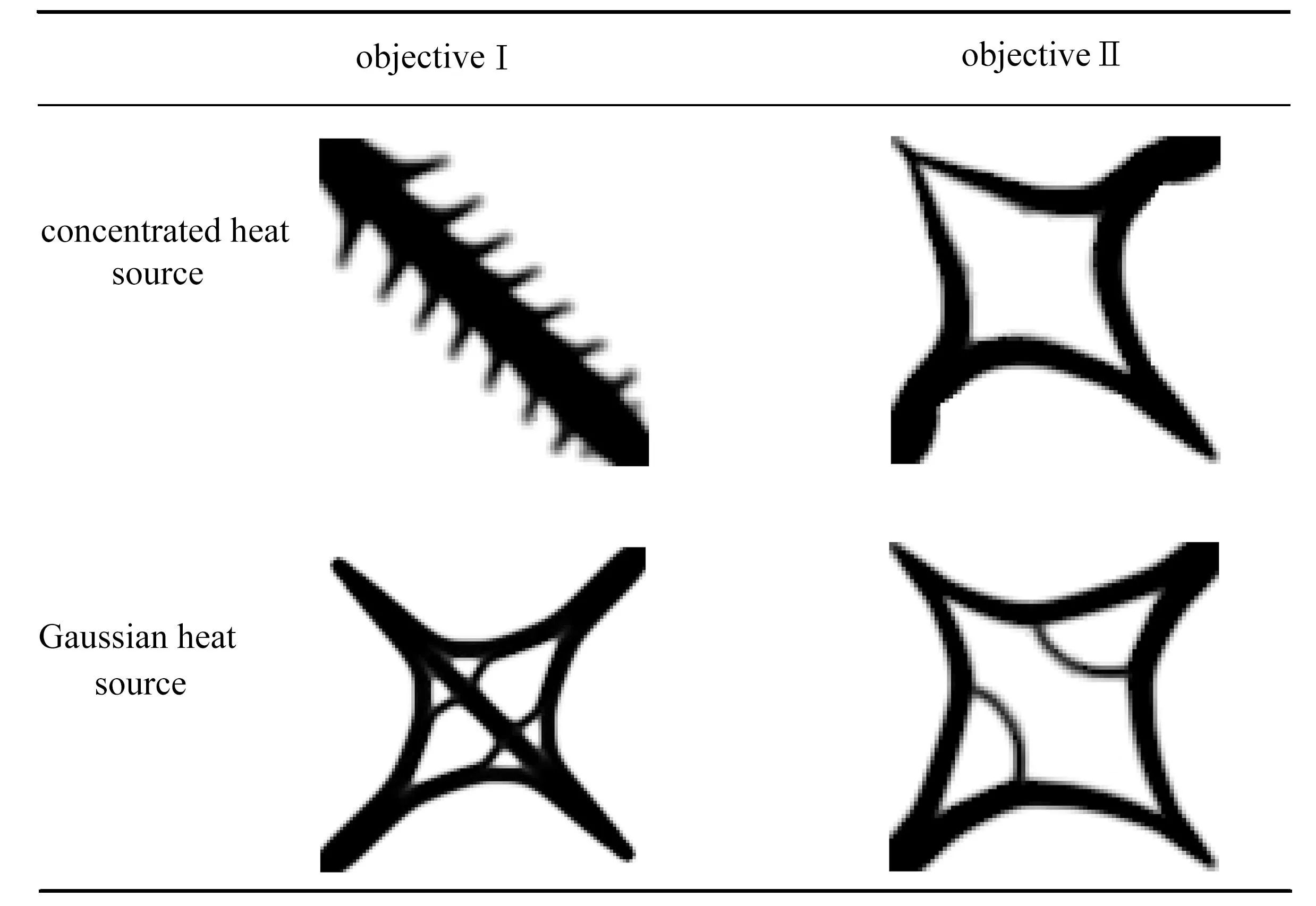
表1 不同热源拓扑优化结果

图7 稳态热传导与移动热源不同速度的优化结果
图7中考虑了移动热源瞬态效应对传热结构的优化结果的影响,随加热时间的不同,其瞬态效应明显,可与图6中固定热源的传热结构瞬态热传导进行对比.Gauss移动热源速度较为缓慢时,其传热材料的拓扑构型瞬态效应明显,沿移动路径向恒温点传热,材料聚集于热源移动路径周围.一定时间内,当热源在路径上处于高速移动时,可以将其视为固定在路径上的稳态热源.Gauss热源沿路径移动,热源速度的变化导致整体结构的温度并非稳态温度场,因此,非稳态的温度变化必须要考虑移动热源在瞬态效应下对传热结构的热传导拓扑优化设计.
图8为Gauss热源移动速度下,传热结构的目标函数随迭代步数的变化.在迭代过程中,目标函数能快速收敛到最优解,不同速度的移动Gauss热源对于传热结构优化迭代过程会有一定影响,产生轻微波动,但整体趋势平缓,证明该方法具有较好的稳定性.
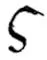
由图9可得出其优化后的材料最高温度变化趋势.两个优化目标随体积分数变化的温度变化规律,其温度变化趋势呈现一致性,即随着传热材料的增加,移动热源下的整体结构最高温度下降明显.目标Ⅱ在对角线路径随材料体积变化的最高温度小于目标Ⅰ,而优化目标Ⅰ的温度变化幅度明显比目标Ⅱ更迅速.
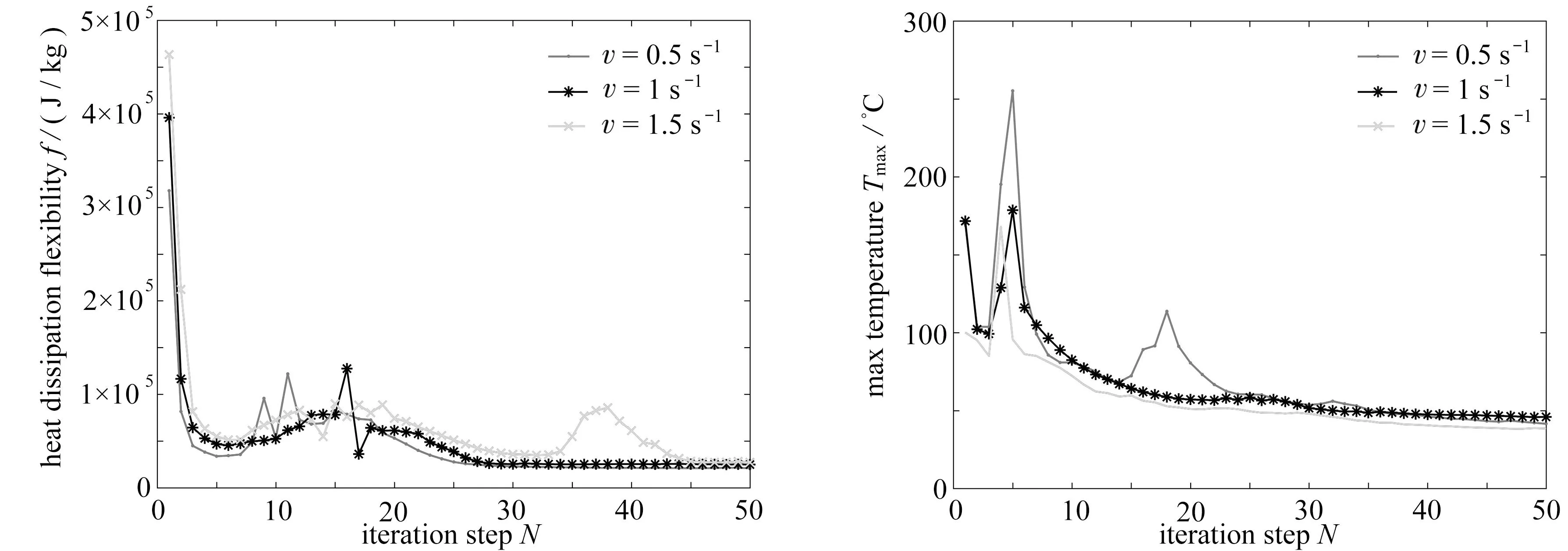
(a) 目标Ⅰ (b) 目标Ⅱ (a) Objective Ⅰ(b) Objective Ⅱ图8 不同热源速度下的目标函数随迭代步数变化曲线

图9 最高温度变化
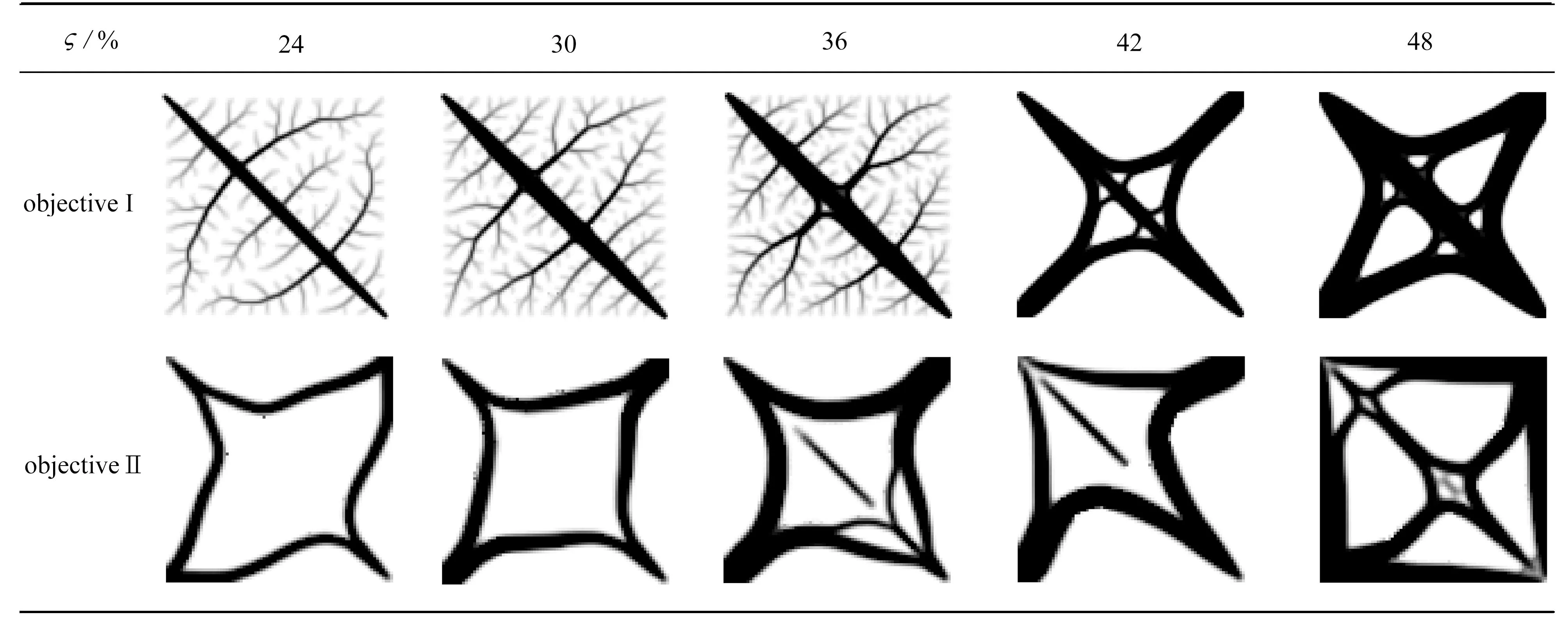
表2 材料体积占比不同下拓扑优化结果
如表2所示,随着设计域体积分数的递增,两个目标优化后的拓扑构型材料的分布具有一定的规律.以散热弱度最小化为优化目标,材料占比较小时,其传热结构不够稳定,受移动热源瞬态效应影响较大,随体积分数的增加,优化后的拓扑结构趋于稳定,材料向热源移动路径集中,同时向0 ℃点延伸.区域温度最大值最小化的优化目标,其优化后的材料分布逐渐向对角线移动路径周围集中靠拢,即从加热路径向零温度点延伸的变化,材料占比足够大时,优化后的构型边界清晰、结构合理.
2.2 方形区域路径
针对区域路径移动热源的结构散热优化,设计域几何尺寸同样取1 mm×1 mm×0.8 mm,将其离散为80×80的四节点方形单元.热源移动区域路径如图10所示,令其设计域四顶点为温度恒定为0 ℃的恒温材料,其余材料为隔温绝热材料.
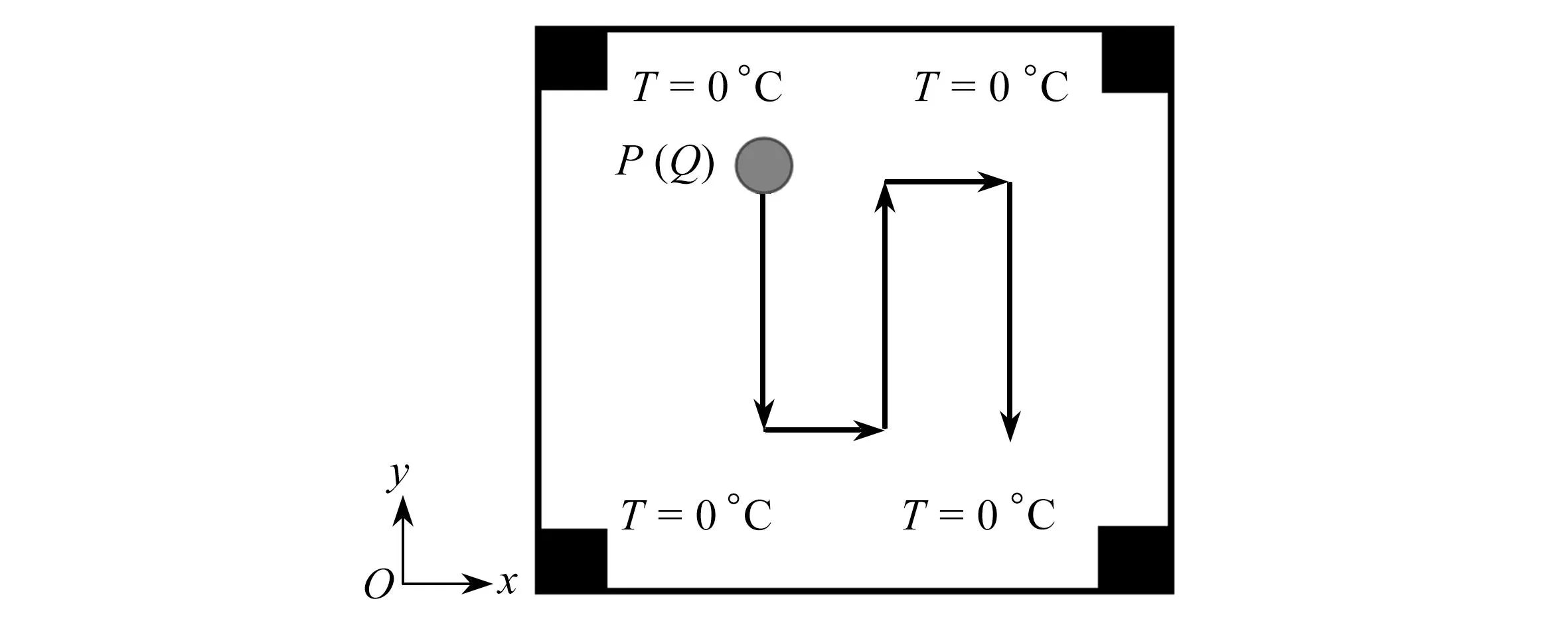
图10 区域S形路径结构设计域
如图11所示,给定移动热源速度v=1 s-1,在离散单元中取中心20×20的移动范围,以热源加热时间为变量,考虑Gauss移动热源对传热结构的拓扑结果具有明显的瞬时性,其材料分布随着加热时间的变化边界更加清晰,结构更加合理.

图11 S形路径移动热源的拓扑构型
Gauss移动热源在离散的结构单元内部区域进行移动,规划热源移动路径范围,使其分别在单元中心区域以5×5,10×10,20×20,25×25的方形单元范围内,移动速度为0.5 s-1经过1单元,利用奇偶性改变运动方向进行S形路径移动,控制迭代次数直至达到优化结构的传热路径最佳.优化拓扑构型列于表3.
根据优化结果显示,在针对目标Ⅰ进行优化时,同一速度Gauss移动热源的在不同移动范围内的运动对传热结构优化结果具有一定影响,运动范围相对整体结构较小时,其热源可近似为固定点热源,其拓扑构型会受热源瞬态效应的影响,构型分枝较多,其温度分布受到移动热源运动终点的影响呈现非对称性.然而,拓扑结果呈现一定规律性,在热源移动区域较小时,进行传热优化的结构其主散热结构仍然是向角点延伸,随着热源移动区域的增大及加热时间的增长,角点延伸区域材料分布越来越多,最终呈现X形结构.随着运动范围占据整体结构的比例上升,散热材料集中分布在运动路径并向恒温点发散,其拓扑构型呈现出X形,中间温度较高区域也随之变大,最高温度点位于热源运动终点处并偏向与位置最近的恒温点散热.
由区域温度最大值最小化为目标的拓扑结果可知,当移动热源小范围运动时,其拓扑构型呈现X形, 温度分布大体与拓扑构型重合, 中心移动范围扩大, 其温度分布不再沿其拓扑构型, 受运动终点的位置影响较大.

表3 Gauss移动热源不同移动范围的拓扑构型
对比不同目标函数下的拓扑构型及温度云图, 在相同热源移动区域下, 目标Ⅰ温度幅值明显高于目标Ⅱ.移动区域较小(5×5)时,热源作用时间短,因此热源瞬态效应明显.目标Ⅰ优化结构传热路径较为复杂,路径尚未连接恒温点,整体设计域温度偏高,热源最高温度高达243.87 ℃;目标Ⅱ优化后的构型形成了更为高效的传热路径,设计域温度最大温度仅为73.19 ℃.移动区域的增加使优化后地路径有效地连通了恒温顶点,传热材料分布更加集中,温度得到有效降低.相比目标Ⅰ优化后的温度分布,随着移动路径的变化,其目标Ⅱ整体结构最高温度更低,以区域温度最大值最小化为目标的拓扑构型相比以最小散热弱度为目标的优化,在考虑移动热源的瞬态情况下具有更佳的散热效果.
3 结 论
1) 本文以对角线路径为例,对Gauss热源模型移动过程中温度分布进行模拟,验证了将Gauss移动热源作为热载荷应用于结构优化的有效性和可行性.
2) 基于变密度法建立了考虑移动Gauss热源瞬态效应的传热结构拓扑优化模型,分析了不同优化目标下的拓扑构型.算例表明,材料比例小于36%时,不同目标的温度赋值变化幅度较大,超过后最高温度趋向稳定降低.调整散热材料体积占比,可以得到传热更佳的拓扑构型,验证了该方法的有效性.
3) 优化结果表明,基于控制变量的思想,不同Gauss热源移动速度、移动路径范围以及材料体积占比优化的拓扑构型均会受到热源瞬态效应的影响.温度云图显示目标Ⅱ优化后的结构整体温度明显低于目标Ⅰ的优化结构,最高温度仅为目标Ⅰ的1/2左右.不同优化目标的传热结构优化结果存在一定的差异性和规律性,可为将来工程应用中考虑移动热源的传热结构拓扑优化设计研究提供理论基础.

