变速抽水蓄能电机在发电工况不同转速下磁场和损耗研究

韩继超,董桀辰,张 勇,孙玉田,李桂芬,张春莉,胡金明,于鸿浩

(1.水力发电设备全国重点实验室(哈尔滨电机厂有限责任公司),哈尔滨 150040;2.哈尔滨电机厂有限责任公司,哈尔滨 150040;3.哈尔滨大电机研究所,哈尔滨150040;4.哈尔滨理工大学,哈尔滨 150080;5.雅砻江流域水电开发有限公司,成都 610051)

0 前言

近年来,我国提出了“中国二氧化碳排放力争于2030年前达到峰值,努力争取2060年前实现碳中和” 的发展目标[1]。因此加快可再生能源在电力系统中的应用已成为当下最重要的研究内容之一[2]。目前我国风电、太阳能电站的装机容量已位居世界前列,但受到地理位置、气候条件等环境因素的影响,风力与太阳能发电具有间歇性与随机性,这会导致电能质量下降,调相、调频、调压与调峰填谷能力下降,影响电力系统的安全可靠运行[3-5]。我国水力资源相对丰富,水电本身也是一种优质的可再生能源。抽水蓄能电站的建设可有效的实现电力储能、调相、调频和调峰填谷[6-9]。因此大力发展抽水蓄能电站不仅可以有效地减少碳排放,更对电力系统的安全稳定运行有着重要的意义。

目前为止,我国抽水蓄能电站大多数采用凸极同步电机,其转子侧加直流励磁,受静态稳定极限的约束,无法进入深度吸收无功的运行状态。同时转子磁场相对于转子的位置是固定不变的,因此进行有功与无功调节时必然会伴随转子的机械过渡过程,而变速抽水蓄能电机转子侧为隐极结构,通过调节三相对称交流励磁绕组内励磁电流的频率、幅值和相位来调节转子磁场大小和位置,从而实现有功与无功的独立调节[10-14]。传统的抽水蓄能电机恒定转速运行,在抽水(电动机)工况下运行时由于无法对转速进行调节而导致只有一条水泵特性曲线,在扬程确定时只有一个输入功率与之对应;在发电机工况下运行时转速固定不变,无法适应因水头变化或负载变化引起的转子转速变化,会引起抽水蓄能电机功角摆动,甚至影响抽水蓄能电机的安全稳定运行,而转子交流励磁变速抽水蓄能发电电动机通过调节转子电流的工作频率来改变机组的运行转速,扩大水泵水轮机运行水头与扬程比范围并获得最佳性能指标,很多学者开展了变速抽水蓄能发电电动机关键技术的研究工作[15-19]。本文以一台10MW 变速抽水蓄能发电电动机为例,建立了10MW 变速抽水蓄能发电电动机二维电磁场的数学方程和物理模型,对变速抽水蓄能发电电动机的电磁场数学方程进行了计算,研究了不同转速时变速抽水蓄能电机在发电机工况下磁密的分布规律,分析了不同转速下定子铁芯损耗和转子铁芯损耗占总铁芯损耗比例的变化规律,通过试验测试验证了计算结果的准确性。

1 变速抽水蓄能电机数学模型分析

变速抽水蓄能电机定子与转子均采用三相对称绕组,其结构与等效电路如图1所示。

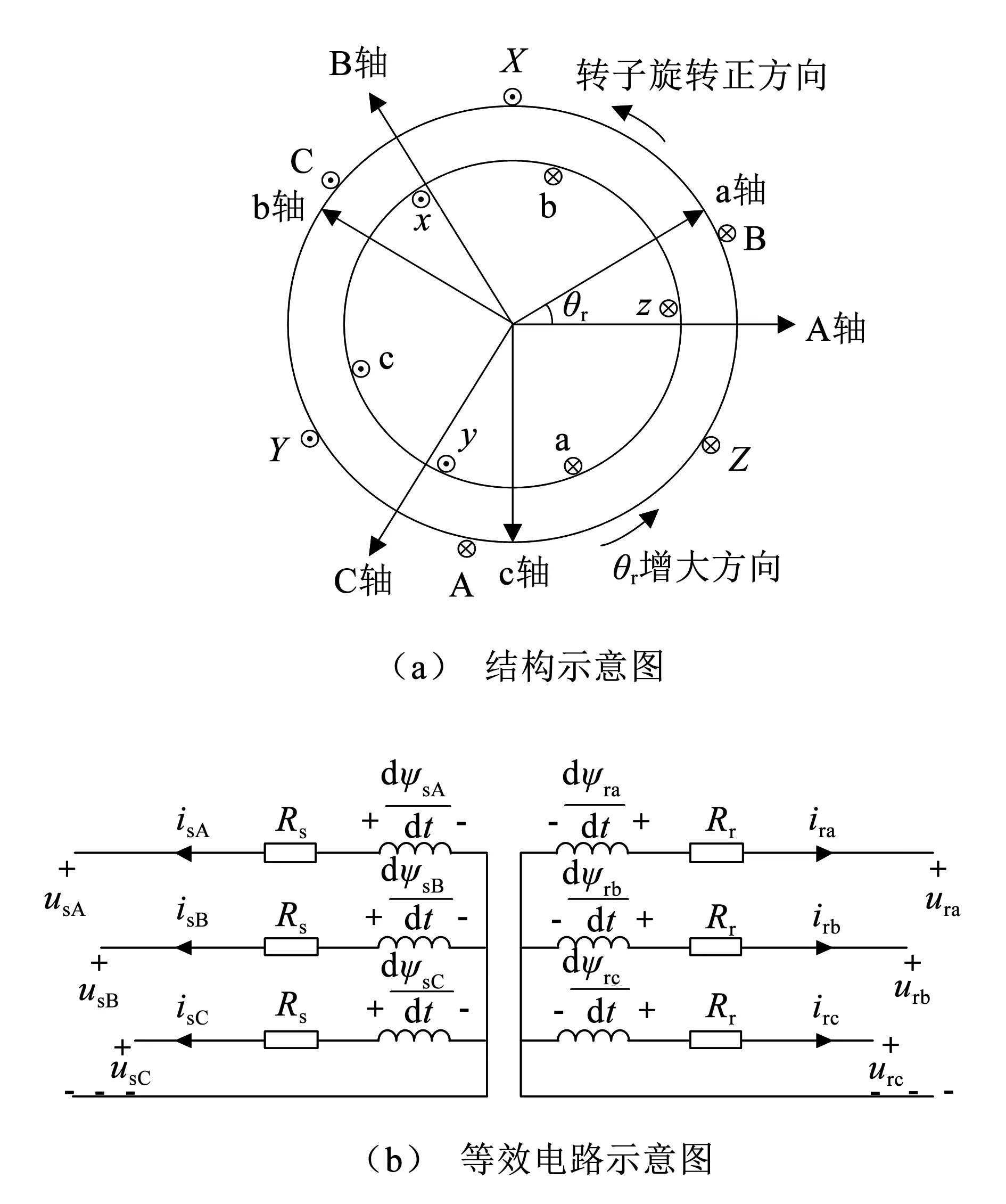
图1 变速抽水蓄能电机示意图

变速抽水蓄能电机的定子绕组与转子绕组三相绕组均按照逆时针排列,定子三相绕组采用A、B、C表示,转子三相绕组采用a、b、c 表示。转子旋转电角速度为ωr,转子a 相轴线与定子A 相轴线之间的夹角为θr,ωr与θr之间满足ωr=dθr/dt。本文中定子绕组的电气值由下标sA、sB、sC 表示,转子绕组的电气值由下标ra、rb、rc 表示。图1 中usA、usB、usC分别是定子A 相、B 相、C 相的电压,isA、isB、isC分别是定子A 相、B 相、C 相的电流,Rs为定子电阻,ura、urb、urc分别是转子a 相、b 相、c 相的电压,ira、irb、irc分别是转子a 相、b 相、c 相的电流,Rr为转子电阻。

1.1 电压方程与磁链方程

以变速抽水蓄能电机的发电机工况为例,假设电机气隙均匀且不计铁芯饱和,将转子绕组电气参数折算到定子侧,可得变速抽水蓄能电机在发电机工况下数学模型的矩阵形式[20-22],即

式中,U为定子和转子绕组端电压矩阵,U=[usAusBusCuraurburc]T;I为定子与转子绕组电流矩阵,I= [isAisBisCirairbirc]T;Ψ为定子和转子绕组磁链矩阵,Ψ= [ψsAψsBψsCψraψrbψrc]T;R为定子和转子绕组电阻矩阵,R=diag[RsRsRsRrRrRr];L为定子和转子绕组电感矩阵,可表示为:

其中,Ls、Lr、Lsr可表示为:

式中,Ms为定子绕组相间互感;Mr为转子绕组相间互感;Msr为定子绕组和转子绕组间的互感,Msr=2Ms=2Mr;Lss为定子绕组自感,Lss=2Ms+Lsσ;Lsσ为定子绕组漏感;Lrr为转子绕组自感,Lrr=2Mr+Lrσ;Lrσ为转子绕组漏感;θr为定子A 相轴线与转子a相轴线之间的夹角。

1.2 电磁转矩方程

根据虚位移原理,结合式(1),可推出变速抽水蓄能电机电磁转矩表达式为:

式中,Te为变速抽水蓄能电机电磁转矩;p为变速抽水蓄能电机极对数。

代入电流矩阵I和电感矩阵L,可得电磁转矩表达式,即:

1.3 运动方程

变速抽水蓄能电机运动方程为:

式中,ωr为转子旋转电角速度;Tm为变速抽水蓄能电机机械转矩;J为变速抽水蓄能电机转动惯量;kF为阻尼系数;kθ为扭转弹性转矩系数。

2 变速抽水蓄能电机二维电磁场数值计算

表1 给出了10MW 变速抽水蓄能电机的基本设计参数。

表1 10MW 变速抽水蓄能电机的基本设计参数

建立了10MW 变速抽水蓄能电机二维电磁场数学方程和物理模型,其二维电磁场数学方程如下:

式中,Az为矢量磁位;Js为电流密度矢量;μ为介质磁导率;Γ1为定子外表面圆周;Γ2为转子内表面圆周。

本文采用有限元方法对变速抽水蓄能电机在发电工况下五种转速时二维电磁场数学方程进行了计算,图2 给出了10MW 变速抽水蓄能电机二维电磁场的物理模型。

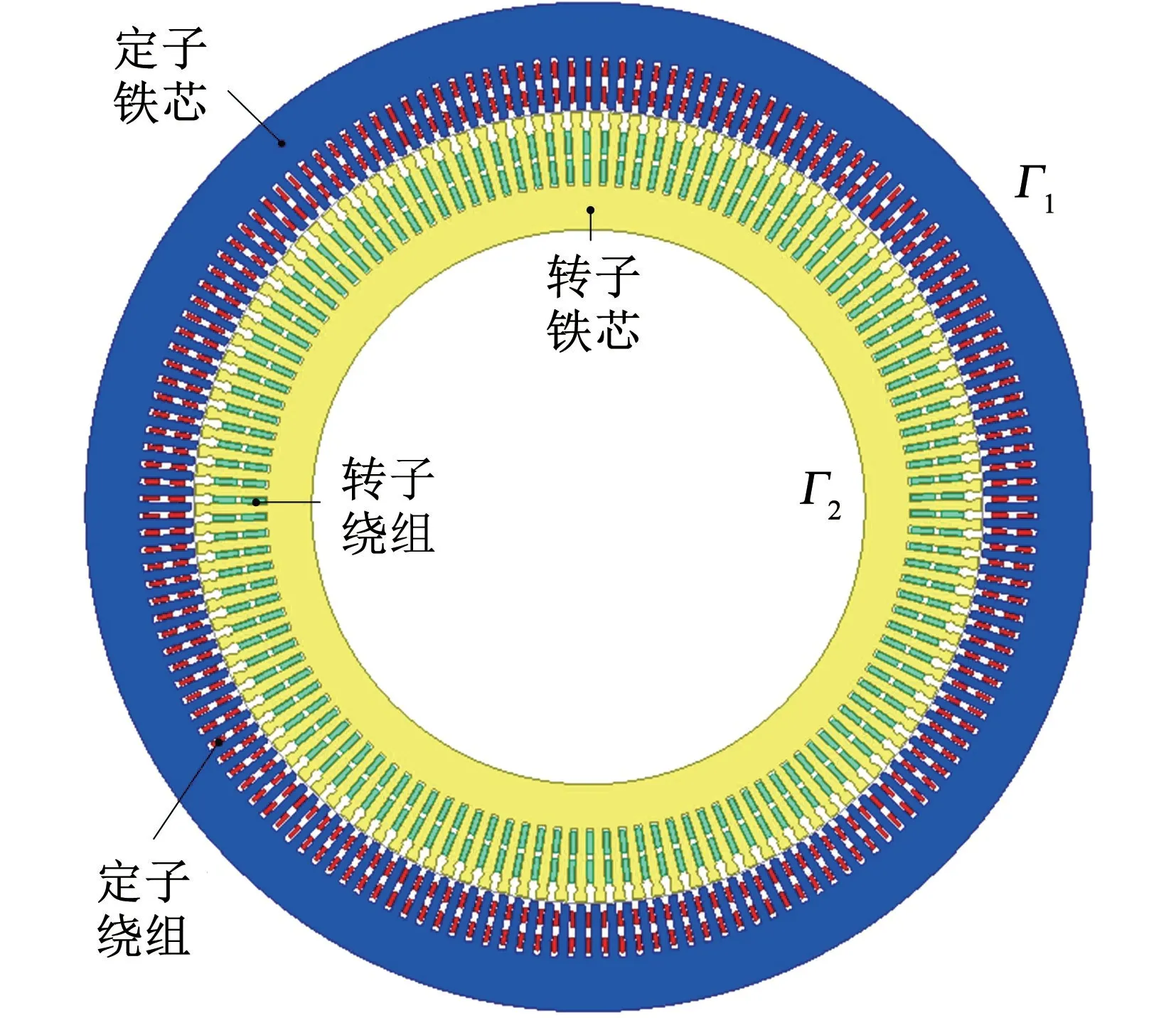
图2 变速抽水蓄能电机二维电磁场的物理模型

10MW 变速抽水蓄能电机的转速变化范围为460～540r/min,本节对变速抽水蓄能电机在超同步速(540r/min)时二维电磁场进行了数值计算。图3 和图4 分别为10MW 变速抽水蓄能电机在发电机工况下超同步速(540r/min)时定子电压波形图和定子电流波形图,可以看出定子电压波形和定子电流波形的三相对称度均较好。通过变速抽水蓄能电机二维瞬态电磁场数值计算得到的定子线电压有效值和定子线电流有效值与通过电磁计算程序得到的定子线电压有效值和定子线电流有效值较为接近。

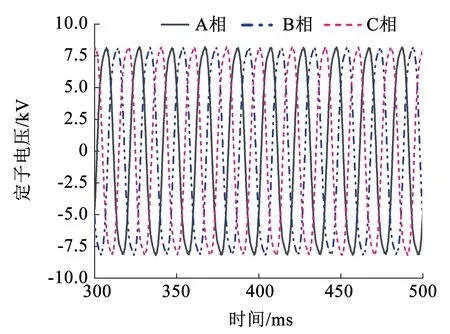
图3 超同步速(540r/min)时定子电压波形

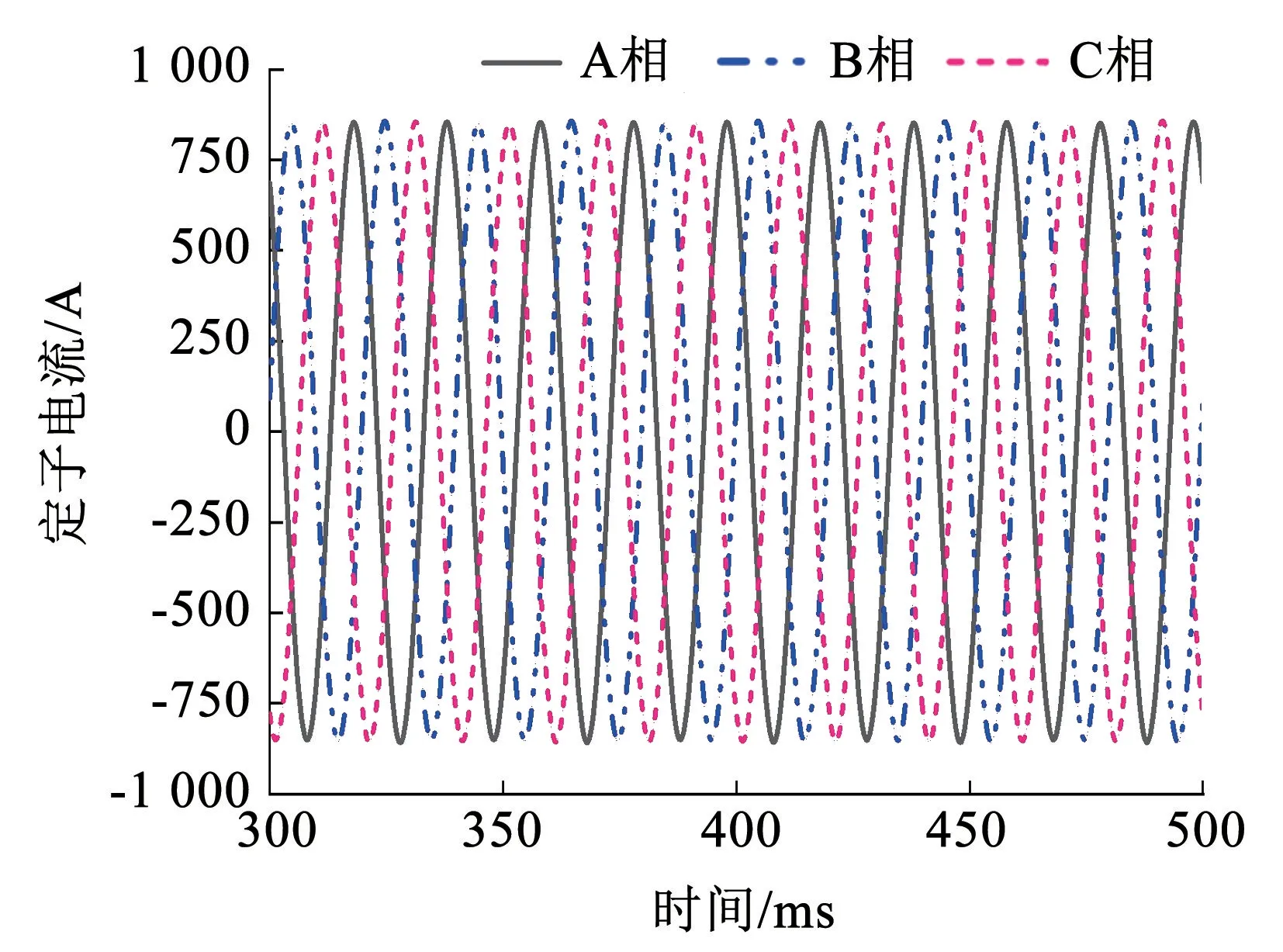
图4 超同步速(540r/min)时定子电流波形

3 不同转速下变速抽水蓄能电机磁密变化规律的研究

本节对变速抽水蓄能电机在发电机工况下亚同步速(460r/min 和480r/min)、同步速(500r/min)、超同步速(520r/min 和540r/min)五种不同转速下变速抽水蓄能电机二维电磁场进行了数值计算,研究了不同转速下变速抽水蓄能电机内磁密的变化规律。

图5 给出了不同转速时10MW 变速抽水蓄能电机的磁密云图,不同转速下变速抽水蓄能电机内部磁密分布大致相同,变速抽水蓄能电机在500r/min 时磁密较高。

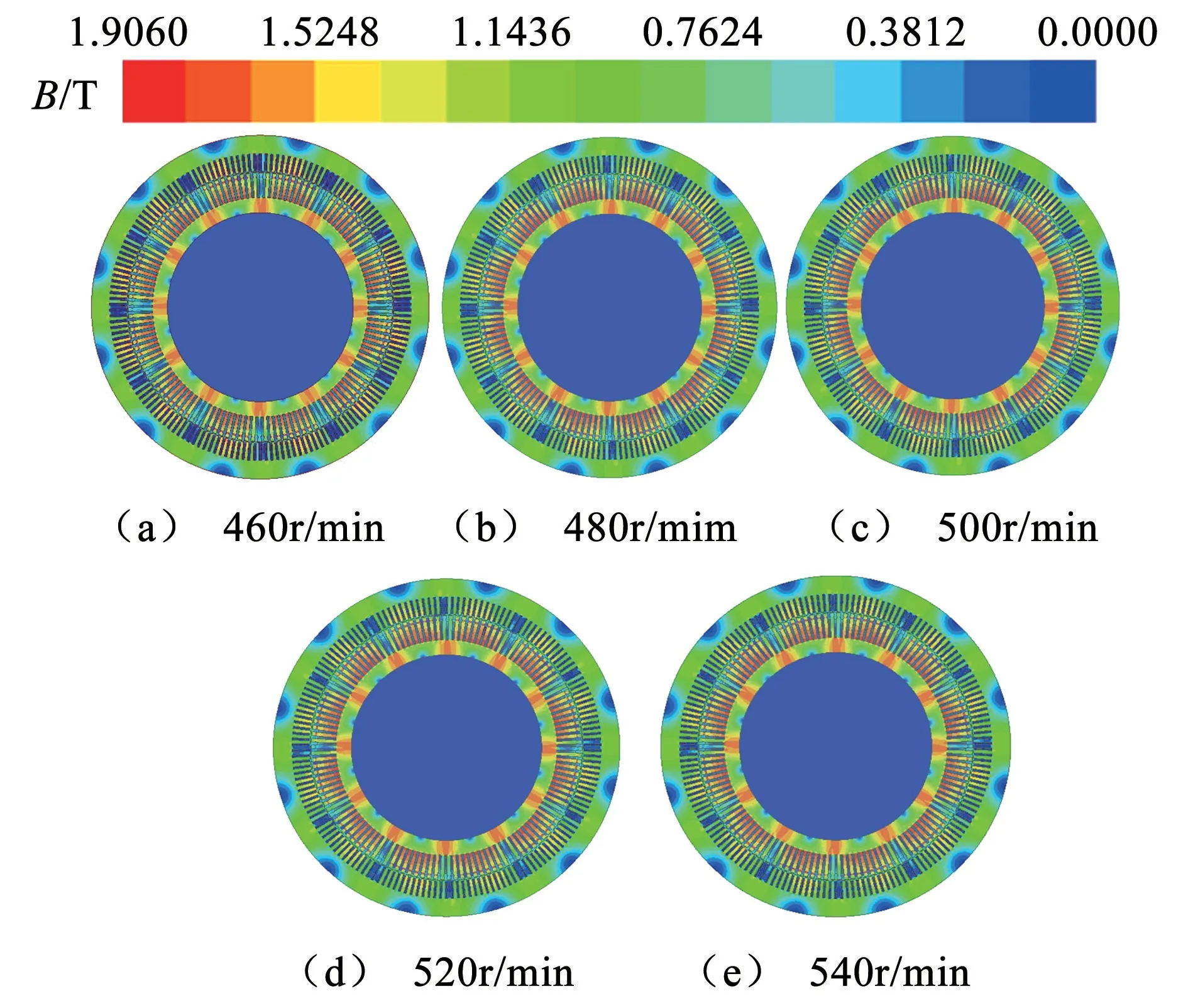
图5 不同转速时变速抽水蓄能电机的磁密云图

图6 为不同转速时10MW 变速抽水蓄能电机一对极下气隙磁密的基波和各次谐波对比图。可以看出五种转速下各次谐波幅值相差较小。变速抽水蓄能电机在转速为460r/min 时基波幅值较大,在转速为540r/min时三次谐波幅值较大。气隙谐波分解可以确定变速抽水蓄能电机内各次谐波磁密幅值,为准确计算变速抽水蓄能电机表面损耗奠定基础。

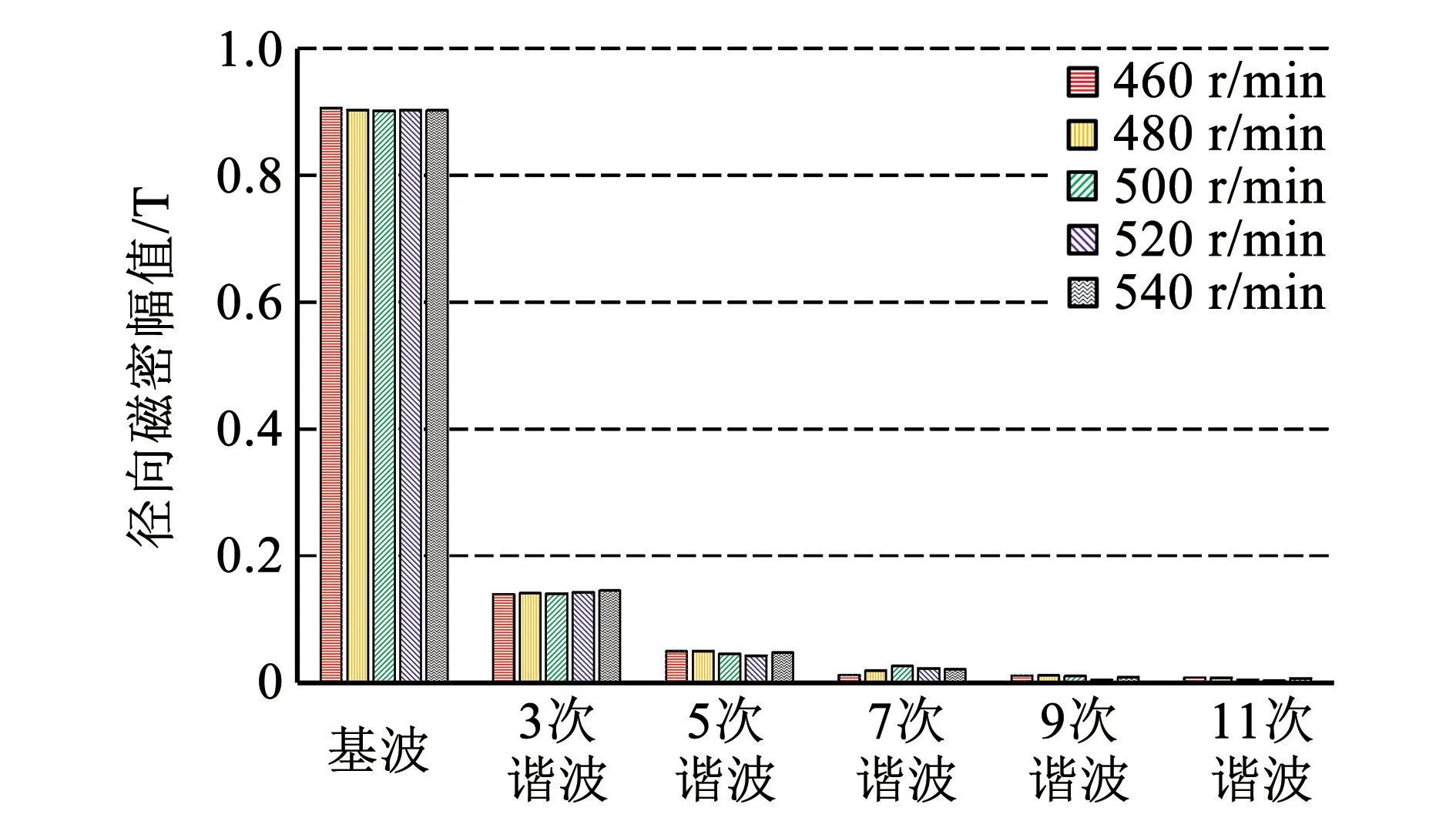
图6 不同转速时10MW 变速抽水蓄能电机气隙磁密的基波和各次谐波对比图

4 不同转速下变速抽水蓄能电机定子铁芯损耗和转子铁芯损耗的分析

变速抽水蓄能电机定子铁芯损耗和转子铁芯损耗由磁滞损耗、涡流损耗和附加铁芯损耗三部分组成,铁芯损耗计算公式如下[23-24]:

式中,Pν为铁芯损耗;Ph为磁滞损耗;Pc为涡流损耗;Pe为附加铁芯损耗。

磁滞损耗Ph主要取决于磁滞环所围面积与磁通密度交变频率,即:

式中,Bm为磁密幅值;kh为磁滞损耗系数;f为频率。

涡流损耗和附加铁芯损耗主要取决于磁通密度变化率。当磁密波形为正弦波时,可以得到在频域上铁芯损耗的计算公式,即:

式中,kc为涡流损耗系数;ke为附加铁芯损耗系数。

图7 给出了不同转速下变速抽水蓄能电机定子铁芯损耗和转子铁芯损耗占总铁芯损耗的比例分配图。由于转子绕组通有三相交流电,导致转子铁芯损耗也较高。变速抽水蓄能电机在转速为500r/min 时定子铁芯损耗占比较高,转子铁芯损耗占比较低。转子铁芯损耗与频率有关,变速抽水蓄能电机在转速为460r/min 和540r/min 时转子绕组所通励磁电流的频率为4Hz,转子铁芯损耗占比较高。随着变速抽水蓄能电机转子转速的增加(从460r/min 到540r/min),转子铁芯损耗占比先逐渐减小后逐渐增加。

图7 不同转速下变速抽水蓄能电机定子铁芯损耗和转子铁芯损耗占总铁芯损耗的比例分配图

5 10MW 变速抽水蓄能发电电动机样机的试验测试

为了验证10MW 变速抽水蓄能发电电动机二维电磁场数值计算结果的准确性,构建了10MW 变速抽水蓄能发电电动机试验测试平台,如图8所示。试验测试平台主要包括变速抽水蓄能发电电动机、拖动机、减速箱、变流器、励磁变压器等。

图8 变速抽水蓄能发电电动机试验测试平台

对10MW 变速抽水蓄能发电电动机进行了试验测试,调节励磁电流和转速,记录定子电压和定子电流。表2 给出了不同转速下10MW 变速抽水蓄能电机实测值与计算结果对比。可见不同转速时10MW 变速抽水蓄能发电电动机的计算结果与实测值较为接近,验证了计算结果的准确性。

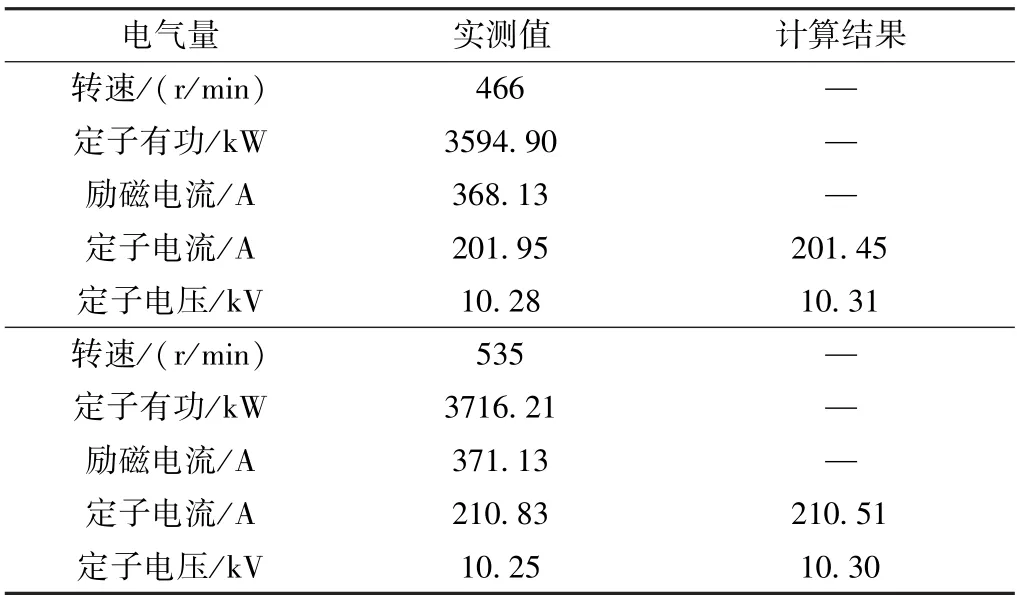
表2 不同转速下10MW 变速抽水蓄能电机实测值与计算结果对比

6 结论

本文对不同转速下10MW 变速抽水蓄能电机的磁密和定转子铁芯损耗进行了研究,变速抽水蓄能电机在500r/min 时磁密较高。变速抽水蓄能电机在转速为460r/min 时基波幅值较大,在转速为540r/min 时三次谐波幅值较大。变速抽水蓄能电机在转速为500r/min 时定子铁芯损耗占比较高,转子铁芯损耗占比较低。随着变速抽水蓄能电机转子转速的增加,转子铁芯损耗占比先逐渐减小后逐渐增加。通过10MW变速抽水蓄能发电电动机样机验证了计算结果的准确性和计算方法的可行性。