海底不均匀沉积层斜向声学原位纵波测量的仿真研究

王 莹,陶春辉*,,张国堙,周建平,3,沈洪垒

(1.上海交通大学 海洋学院,上海 200030; 2.自然资源部海底科学重点实验室,自然资源部第二海洋研究所,浙江 杭州 310012; 3.自然资源部海洋智能观测技术创新中心,浙江 杭州 310012; 4.中国矿业大学 深地工程智能建造与健康运维全国重点实验室,江苏 徐州 221116)

0 引言

海底沉积物声学特性通常用声速、声衰减系数等参数表示,可以用于反演沉积物的物理力学性质,在海洋工程地质评价、海洋声场预报、潜在工程地质灾害评估等领域有着广泛的应用前景[1]。受沉积环境以及沉积物被改造、埋藏后压实与固结等作用影响,从陆架、陆坡到深海盆地,不同沉积单元地层分层,导致沉积层垂向分布不均匀,其声学特性存在着明显的垂向变化[2]。另外,以花岗岩为基底的沉积层中常见孤石分布[3],会造成沉积层的横向分布不均匀。针对这些不均匀沉积层开展声学特性测量方法研究具有重要意义。

海底沉积物的声学特性测量方法主要包括实验室测量与原位测量两种。实验室测量即是在室内测量沉积物样品,方法简单高效,但是样品脱离了海底原始的温度与压力环境,且在搬运过程中可能造成结构的变化,测量精度较低[4]。原位测量是将测量仪器放置在海底沉积物中进行测量,该方法保持了海底原始的温度与压力环境,且最大程度降低了对沉积物的扰动,可以获得高精度的沉积物声学特性[1,5-6]。根据声源与接收换能器相对位置的不同,原位声学测量方式可分为垂向测量、横向测量、孔中测量以及斜向测量四大类[4](图1)。横向测量的发射与接收换能器在同一水平线上,由于受尺寸限制,现有的横向声学原位测量系统只能测所在层位一定水平范围内的沉积物声学特性,很难识别宏观的沉积层空间不均匀性,代表性设备有美国的ISSAMS 系统[7]、ISSAP系统[8]、ACS系统[9]、AA沉积物声衰减测量阵列[10],英国的SPADE探针[11]、SAPPA系统[12],我国自然资源部第一海洋研究所研发的HISAMS系统[13]和BISAMS系统[14]。垂向测量的发射与接收换能器在同一垂线上,其识别垂向不均匀性效果较好,但无法识别横向不均匀性,代表性设备有美国的AL声学长矛测量系统[15],我国自然资源部第二海洋研究所研制的多频海底声学原位测试系统MFI GeoA系统[6]和第二代MFI GeoA系统[16]。孔中测量通常依靠钻机进行装置下放,可实现大深度测量,对水平方向的沉积空间不均匀性具有较好的识别效果,但是难以避免滑行波对测量结果的影响,由于探测波频率通常较高,水平探测距离受到限制,典型代表有传统声波测井。斜向测量的发射与接收换能器呈一定角度倾斜,可获取垂向和横向信息,其识别垂向不均匀性的效果不如垂向测量好,代表性设备有美国的SAMS系统[17],该系统可以获取横向、纵向的沉积层信息,由于探测距离较短,且声速计算方法过于简单,对大深度沉积层空间不均匀性识别效果较差。总体而言,现有的原位声学测量系统主要针对浅表层沉积物声学特性测量,探测深度较浅,且受激发声源频带和接收偏移距等客观因素制约,横向探测范围有限。斜向测量能够同时获取沉积层垂向、横向信息,是获取不均匀沉积层声学特性的有效方法,通过扩大探测距离并优化声速计算方法,将有效推动大深度沉积层原位测量技术的发展。

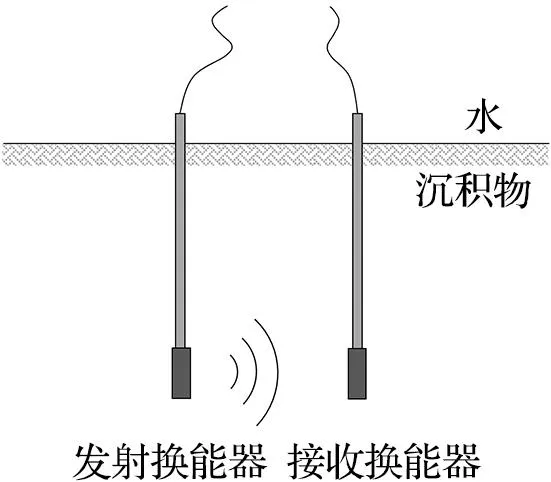
(a)横向测量

(b)垂向测量

(c)孔中测量

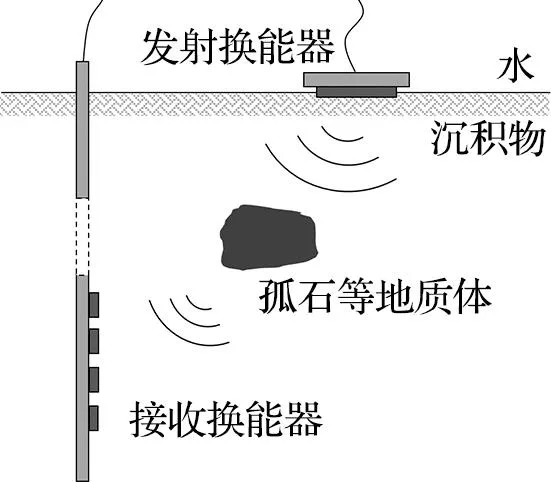
(d)斜向测量图1 四种原位测量方式的示意图Fig.1 Schematic diagram of four in situ measurement methods(图片根据文献[4]改绘。)(Figure was modified from reference[4].)

随着海洋工程建设不断发展,扩大探测范围的趋势明显,由此带来的潜在沉积层不均匀性问题对原位测量方式提出了新的挑战。对此,本研究针对垂向百米和横向十几米甚至更远的双重探测范围内极有可能出现浅层气、孤石等地质异常体的情况,提出一种基于海底沉积层不均匀性的斜向声学原位纵波测量方法,并利用COMSOL软件构建沉积分层和含孤石地质异常体两种不均匀沉积层模型,对分布式斜向声学原位测量方法进行仿真研究,旨在解决斜向测量在获取大范围声学特征时受识别地层不均匀性影响的问题。同时针对斜向测量模式对垂向不均匀性识别效果较差的特点,提出了基于等效偏移距校准的声速计算方法,以期有效识别沉积层不均匀性。

1 斜向声学原位纵波测量方法

斜向声学原位纵波测量方法可同时获取百米深度内沉积层垂向和横向的不均匀性信息,其测量结果可通过声速、声衰减系数等表示。斜向声学原位纵波测量系统包括甲板显控单元与水下测量单元两部分(图2)。其中,甲板显控单元负责数据采集与显示,与水下测量单元通过电源线和信号传输线连接,可实时配置水下测量单元的工作参数,并显示存储采集的声波信号。水下测量单元包括放置于海底表面的声学发射换能器TX与搭载于探杆上的声学接收换能器RX阵列。测量时,利用贯入装置以预设速度v0贯入探杆,将接收换能器阵列全部刚好插入沉积物的时间标记为零时刻。继续贯入深度Δh,发射一次信号并采集数据。每贯入Δh,重复上述操作。Δh取值越小,探测精度越高。

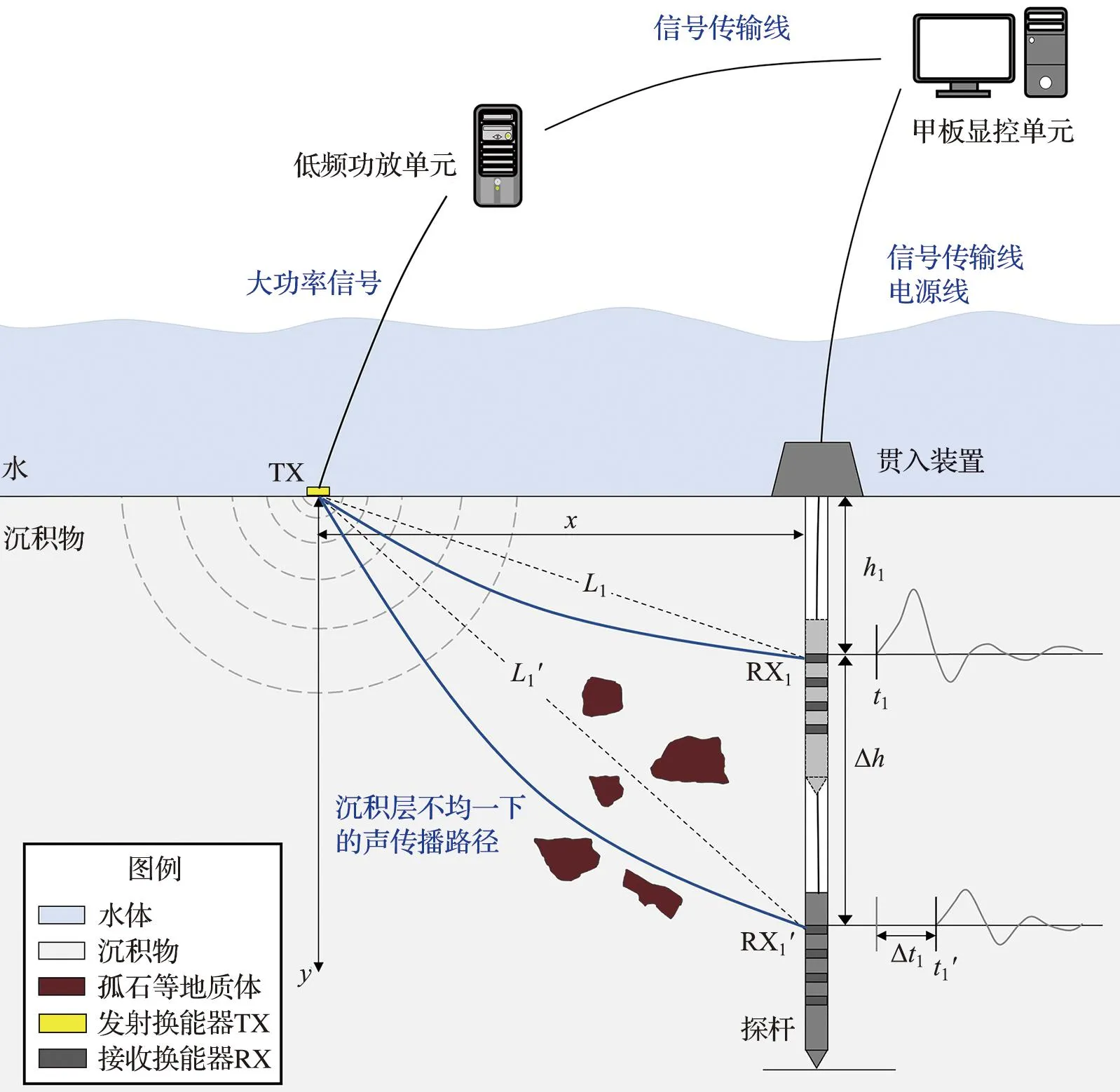
图2 斜向声学原位纵波测量系统及工作原理示意图Fig.2 Oblique acoustic in situ longitudinal wave measurement system and schematic diagram of working principle

该系统尚在研发阶段,缺乏实测数据,因此基于海底原位测量相关文献及工程勘探资料,构建不同沉积层模型,对海底声学原位测量时声在不同沉积层结构中的传播过程进行数值仿真,并根据仿真结果进行声速反演,从而分析该方法对沉积层不均匀性的识别效果。

2 斜向声学原位纵波测量的数值仿真

2.1 声传播特性仿真基础

基于COMSOL Multiphysics压力声学模块,使用有限元方法开展沉积物中声传播的仿真研究。利用微扰理论将声学问题转化为线性问题,在脱离背景属性的情况下进行简化分析。基于能量、质量和动量守恒,假设整个系统中的热力学过程绝热可逆,黏度和导热系数忽略不计,材料属性数据为常数且无热源,将声场描述为由波动方程控制的声压p,波动方程[18]如下:

(1)

2.2 沉积层模型构建

根据东海工程勘探资料构建均匀型沉积层、分层型沉积层、含孤石型沉积层三种模型。为模拟声波在海底半无限连续空间的传播过程,模型主体采用 50 m×60 m的矩形,两侧和底部设置厚度L0为10 m的完美匹配层(perfectly matched layer,PML),以避免模型边界处的反射对仿真结果产生影响。沉积层中的声波瞬态传播过程与沉积物的声阻抗(密度×速度)相关。

东海大陆架宽且沉积层厚[19],为使仿真更符合实际情况,搜集了东海某区域工程勘探中的140个土样资料,其主要特征为:土质类型以淤泥、淤泥质黏土、淤泥质粉质黏土为主,少量为粉砂;干密度ρd为830～1 630 kg/m3;含水率ω为20%～80%。采用湿密度ρ作为仿真密度参数,根据公式ρ=ρd(1+ω) 换算,取值1 600～1 800 kg/m3。参考以往东海沉积物的取样测量及原位测试测量结果,声速范围设定为 1 500～1 700 m/s[1,6,20-21]。模型基本参数见表1。

表1 模型基本参数表Tab.1 Model basic parameter table

设计装置测量环境为浅海,测量时间一般控制在几小时内,假设工作区域变化不大,水深变化不大。为更好地刻化海底原位环境对声传播的影响,考虑压强对于声速的影响,引入背景压强p1(单位:atm,1 atm=101 325 Pa)。假设测量点位处水深为20 m,自海底面(y=0)起,p1可用如下公式表达:

(2)

式中:ρsediment为沉积物的密度,ρwater为上覆水层的密度,y对应图2中的纵坐标。

为充分保证声源发射的连续性,采用域声源的方式来近似点声源,其函数关系式定义为描述空间部分Gx,y与描述时间部分Gt的乘积形式。

Q=Gx,y·Gt

(3)

(4)

(5)

式中:Gx,y为二维平面上的高斯脉冲,Gt为雷克子波, dS表示声源的范围,x、y表示空间中任意点的横、纵坐标,x0、y0表示声源位置的横、纵坐标,f0为发射信号主频,t表示时间。

模型采用笛卡尔坐标系,起点坐标为(0, 0),声源位置坐标为(35, 0);经多次试验,dS取2e-4仿真效果较好;根据系统实际工作情况,频率f0设为1 kHz。

2.3 网格剖分与求解

对均匀型与分层型沉积层模型形状规则的物体,采用映射网格剖分比自由网格剖分质量更好;含孤石型沉积层模型,由于几何形状不规则,选用自由网格剖分效果更为理想。为保证精度,控制沉积物区域最大单元格为波长的1/10。PML区域形状规则,对求解精度并无特殊要求,只需保证信号进入该区域后迅速衰减,因此,采用映射网格剖分,沿PML拉伸方向设置固定单元数为25。

采用向后差分法对0.04 s时间内声波传播过程进行仿真,时间步长设置为1×10-5s。

2.4 建模可靠性验证

沿右侧PML拉伸方向提取横截线声压图像(图3),可以看出进入PML后,信号逐渐衰减,在到达壁面之前声压值已衰减为零,未产生反射信号。表明所采用的仿真模型能够表征真实海底沉积层环境的半无限连续介质声波传播特征。

图3 右侧完美匹配层横截线声压Fig.3 Right perfect match layer transversal sound pressure

3 结果与讨论

3.1 三种沉积层模型仿真结果

3.1.1 均匀型沉积层模型

从均匀型沉积层模型二维平面内声压随时间变化的图像可以看出,自声源发出脉冲信号后,以半球形不断向外扩展(图4a),进入PML后信号衰减剧烈(图4b),传播至边界处无反射(图4c),证明半无限连续的沉积层仿真可靠。

图4 均匀沉积模型中的声传播Fig.4 Acoustic propagation in homogeneous sediments model

在对应均匀型沉积层模型中,声源下方10、20、30、40 m的垂向距离处提取仿真数据,并绘制声压随时间变化的图像,作为接收换能器接收声波信号的记录(图5)。

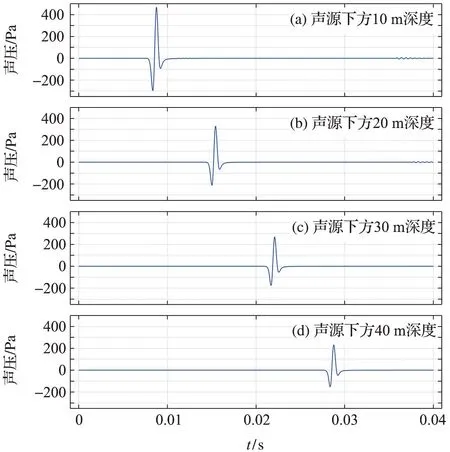
图5 均匀沉积模型中声源正下方接收器声压随时间变化Fig.5 Receiver pressure directly below the acoustic source change with time in the homogeneous sediment model

3.1.2 分层型沉积层模型

在均匀型沉积层模型的基础上构建分层型沉积层模型,上层厚20 m,下层厚40 m(图6a)。根据勘探资料,通常浅层沉积物随深度增加,密度和声速呈增高趋势。故模型上层设置为低速层,详细材料参数取值参考沉积物Ⅰ(表1);下层为高速层,详细材料参数取值参考沉积物Ⅱ(表1)。根据2.3节所述的网格剖分方法,采用映射网格对全部区域进行剖分,得到如图6b所示的由规则矩形构成的疏密不一的网格。

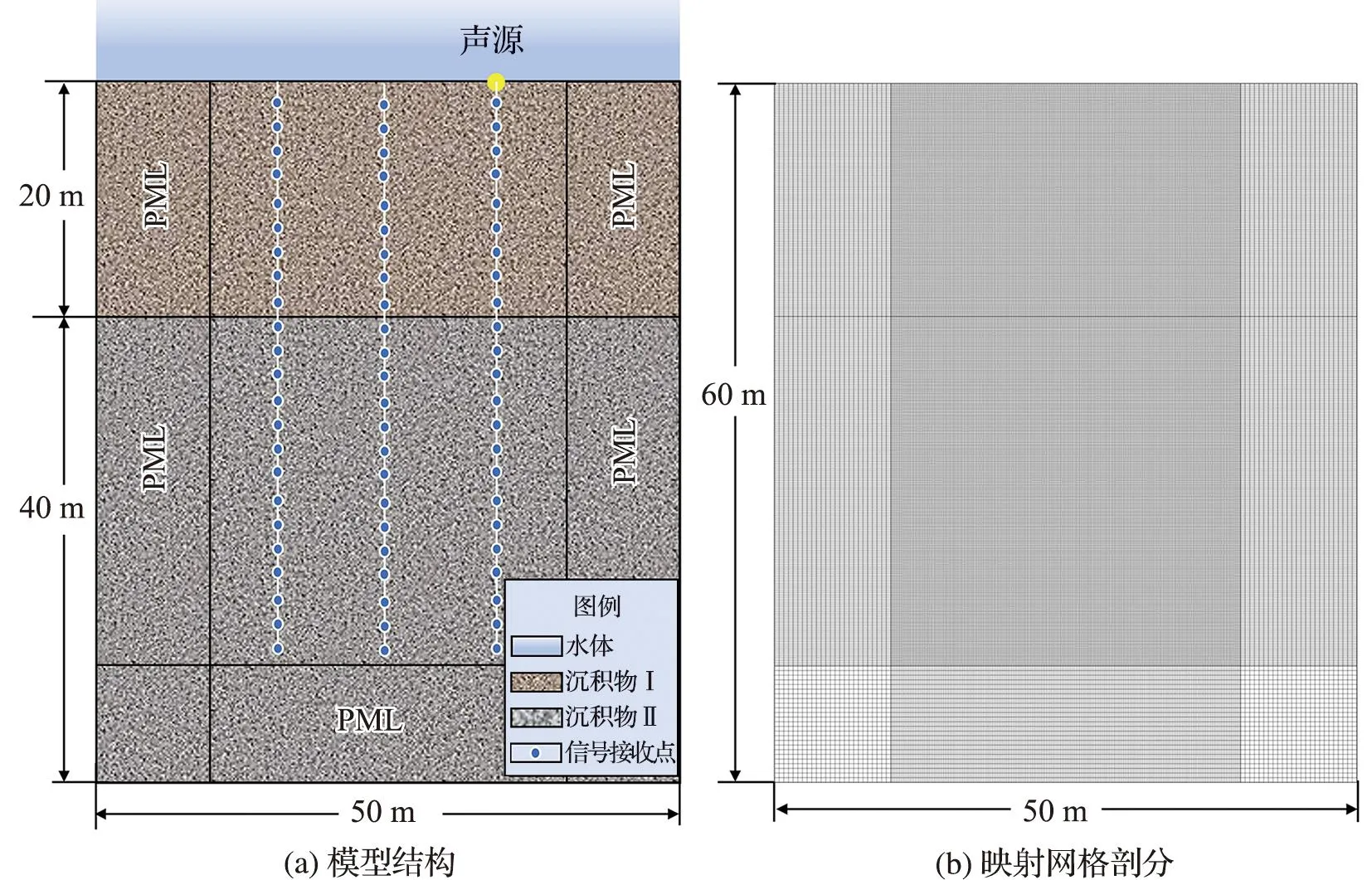
图6 分层型沉积层模型结构(a)及映射网格剖分(b)Fig.6 Model structure (a) and mapping grid subdivision (b) of stratified sedimentary layer model

完成瞬态求解后,可以得到分层型沉积层模型二维平面内声压时空分布规律,图7分别表示在0.021、0.027、0.033 s三个时刻的瞬态声压分布。

图7 分层型沉积层模型中的声传播Fig.7 Acoustic propagation in stratified sedimentary layer model

从图7可以看出,区别于均匀介质,声波传播到低速层与高速层分界面时,一部分能量在界面处被反射(图7a),开始反向传播(图7b),并在海底界面处形成二次反射(图7c)。这表明在测量过程中,如果接收器位置恰好处于分界面附近,收到的波形信号很可能是因存在反射波干扰而失真的。

3.1.3 含孤石型沉积层模型

沉积层中出现与沉积物本身物理性质存在较大差异的地质体,会对声传播过程及其速度与衰减产生较大影响。为探明这种影响,构建含孤石型沉积层模型,并将其与均匀型沉积层模型仿真结果进行对比。根据东海某海域海上风电场项目工程地质勘察资料,在风电场区岛屿、暗礁等附近的残积土、全风化和散体状强风化岩体内多见球状风化体(孤石)。孤石直径一般在0.8～4.0 m。模型中以直径4.0 m球状中风化花岗岩为例,取密度为2 600 kg/m3,声速为3 200 m/s[22]。孤石中心位置坐标设为(30, 20),即孤石设置在相距声源水平距离5 m,垂向距离20 m处(图8a)。孤石与沉积物接触边界的阻抗为8.32×106Pa·s·m-1。采用自由三角形网格对模型进行剖分,沉积物与孤石区域最大单元格为波长的1/10(图8b)。

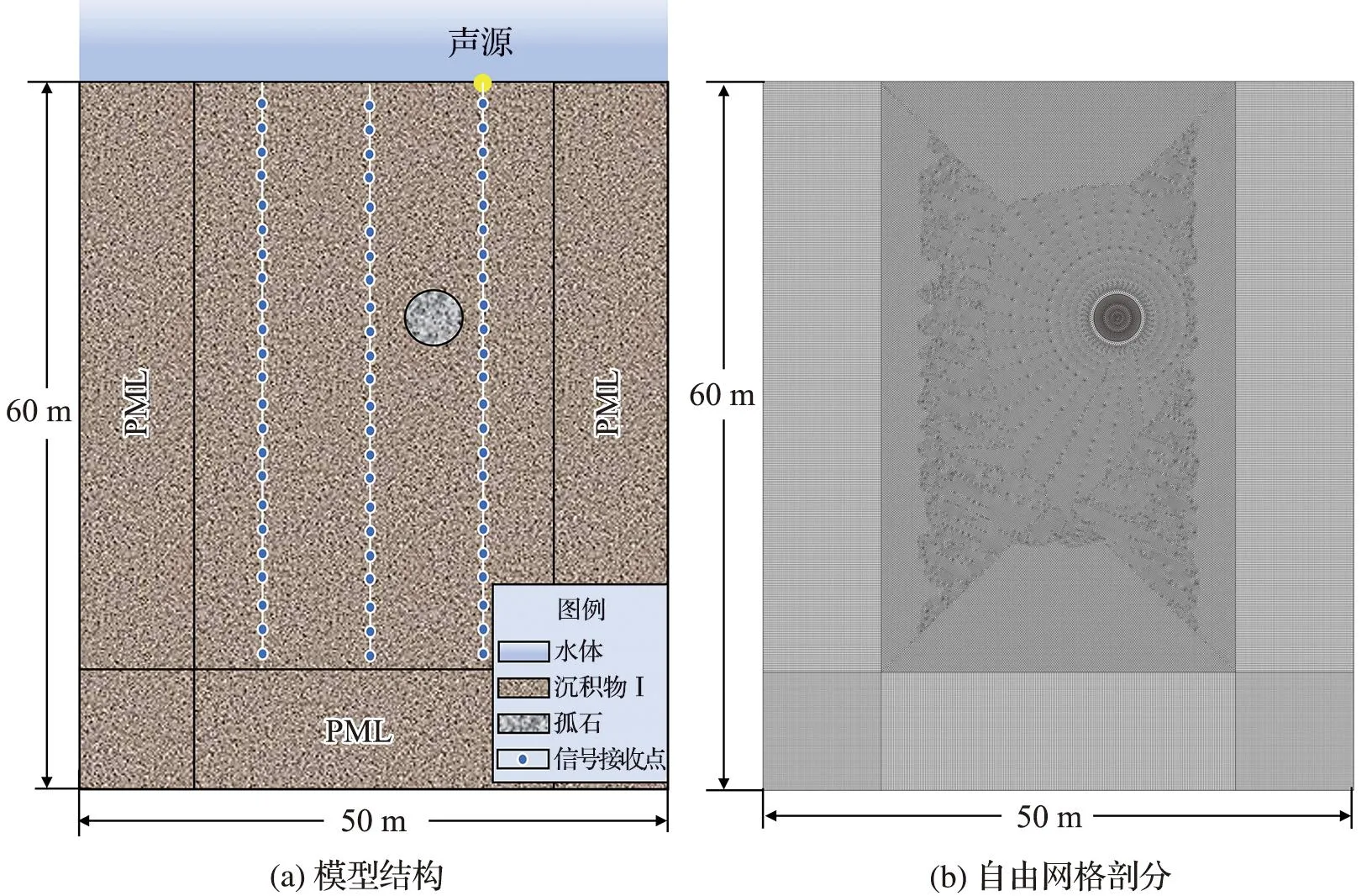
图8 含孤石型沉积层模型结构(a)及自由网格剖分(b)Fig.8 Model structure (a) and free grid division (b) of a sedimentary layer model containing the boulder

对含孤石的沉积层模型求解后,在沿声源发射水平距离10 m处的截线上,30、40 m深度处各取测点,分别绘制测点声压随时间变化的图像(图9)作为接收换能器的波形信号结果。可以看出:相比均匀型沉积层模型,接收到的声压幅值有明显衰减,且波形也发生了明显畸变。

图9 含孤石型沉积层模型接收器声压Fig.9 Receiver sound pressure in a model of a sedimentary layer containing the boulder

图10表示在0.015、0.017、0.033 s三个时刻的含孤石型沉积层模型的声压分布特征。从图中可以看到由于沉积物中存在孤石,声信号在传播过程中一部分会发生透射穿过孤石(图10a),而另一部分在孤石与沉积物接触面发生反射(图10b),并且回波至海底再次反射(图10c),这也是导致信号波形畸变的主要原因。

图10 含孤石型沉积层模型中的声传播Fig.10 Acoustic propagation in a sedimentary layer modle containing the boulder

3.2 声速计算结果与讨论

由于孤石等地质体与沉积层本身存在较大的物性差异,从声学角度可将其视为沉积层中存在的物性不均匀结构体。如果测点附近存在这种物性不均匀结构体,声学原位测量所得的声速往往会与周围沉积层存在显著异常。另外,沉积层也存在垂向的分层物性分界面,可能也会使测量声速结果异常。为了在贯入过程中实时观测到这种异常,利用声波的初至时刻直接计算得到地层声速剖面。

3.2.1 传统井下地震试验声速测量法

在斜向声学原位测量方法中,声速计算算法是决定测量精度的关键。现有声学原位测量系统贯入深度均较浅,忽略了沉积层不均匀性对声速测量的影响。以美国华盛顿大学研制的沉积物声学原位测量系统SAMS[17, 23]为例,其贯入深度为3 m,采用的声速计算方法就是直接使用声信号的传播距离除以声波的旅行时。对于大深度的声学原位测量,由于未考虑沉积层的不均匀性,用该计算方法测量的结果准确度较低。地震波静力触探(seismic cone penetration test, SCPT)是一种大深度的地质勘探方法,它根据同一换能器两次测量结果来进行声速计算。假定到达h1深度发射换能器TX发射声学信号,经过t1时间后信号到达接收换能器RX1。继续贯入Δh后,接收换能器RX1到达RX1′位置处,再次发射声学信号,经过t′1时间后信号到达接收换能器RX1′位置处(图2)。美国材料与试验学会(American Society of Testing Materials, ASTM)在井下地震试验SCPT的标准试验方法中使用的声速计算公式[24]如下:

(6)

式中:cⅠ表示根据井下地震试验SCPT的标准试验方法计算得到的声速,ΔL1是RX1下降前后两次的测量过程中声信号传播直线距离之差,Δt1是前后两次的测量声波旅行时之差,L′1是后一次测量时接收换能器与发射换能器之间的直线距离,L1为前一次测量时接收换能器与发射换能器之间的直线距离,t′1为后一次信号发出到接收器接收所用时间,t1为前一次信号发出到接收器接收所用时间,x为声源水平偏移距。

SCPT的声速算法可应用于海底不均匀性沉积层的大深度测量中:根据沉积层模型的仿真结果,在不同声源水平偏移距下,按测点间距Δh=1 m提取数据;参考李倩宇 等[25]提出的声学原位信号自动拾取方法,采用长短时窗均值比(short term average/long term average, STA/LTA)结合峰值校正方法拾取声波初至时刻;用公式(6)计算得到测点处声速,并绘制声速剖面图像(图11)。对于分层型沉积层模型:在x=0 m 的垂向测量时,公式(6)的计算结果与假定值基本一致;但在x=20 m的斜向测量时,在声速假定值为1 700 m/s的沉积层中,声速计算结果最高值为 1 934.4 m/s。由公式(6)计算得到的声速结果在遇到沉积层分界面时异常偏高。对于含孤石型沉积层模型,在距离声源0、10、20 m测量时均能明显观察到由于孤石存在导致的声速曲线异常情况(图11d～11f),分别在27、22、33 m处声速开始出现异常。斜向测量声速结果偏离假定值更大,更易识别。上述结果表明,斜向声学原位纵波测量方法能识别到位于发射和接收范围内的孤石,相比垂向测量在识别水平不均匀性方面具有明显优势。

图11 不同模型在不同水平偏移距时的声速剖面Fig.11 Sound velocity profiles of different models at different horizontal offsets

对比测点间距Δh=1 m时,不同声源水平偏移距下根据分层型沉积层模型的仿真数据得到的声速计算结果,随着声源水平偏移距增大,按照公式(6)计算得到的声速结果在遇到沉积层分界面时的异常偏高愈明显。原因是该公式忽略了复杂地质情况导致的声线弯曲,将从声源发射到接收点处的声传播路径近似为直线。以本文提出的分层模型为例,声源距接收器存在一定水平偏移距,根据斯涅尔定律,声波从声速小的介质进入声速大的介质时,折射角大于入射角。此时,真实的声传播路径与公式(6)表示的路径长度不符,故依据有限元仿真结果代入公式(6)得到的计算声速与假定声速存在较大偏差。

3.2.2 基于水平偏移距校准的原位声速测量法

在沉积层情况未知的条件下,为获取更贴近真实情况的实时声速剖面,在公式(6)的基础上进行改进,引入权重系数α,以降低声源水平偏移距增大加剧声线弯曲带来的测量结果异常突变效应。优化后的声速计算公式如下:

(7)

式中:cⅡ表示优化后的声速计算公式计算得到的声速;α是权重系数,取值范围为0～1,与声源水平偏移距大小有关。通过多次仿真发现,声源水平偏移距离为20 m,α取值为0.5时,声速计算效果最优。

为进一步明确原位声速测量的影响因素,通过调整每次下降的深度,得到不同测点间距Δh下的声速剖面结构,并验证公式(7)的计算效果(图12)。对于分层型沉积层模型,在声源水平偏移距x=20 m,Δh为2、1、0.5和0.2 m时,根据公式(7)计算的声速范围分别为1 494.8～1 722.9、1 480.8～1 720.8、1 430.6～1 767.3 和1 332.9～1 925.0 m/s,公式(7)的计算结果比公式(6)更贴近于假定沉积层声速结构(图12a～12d)。结果表明,不同Δh下,分层界面位置也随之变化,Δh越大,沉积层分界面识别滞后的效应越明显。

图12 不同模型在不同测点间距时的声速剖面Fig.12 Acoustic velocity profiles of different models at different measuring point spacing

上述规律不仅适用于分层型沉积层模型,对含孤石型沉积层模型同样适用。对于在距声源水平距离5 m、垂向距离20 m处存在孤石异常体的沉积层模型,当声源水平偏移距x=20 m,Δh为2、1、0.5和0.2 m时,根据公式(7)计算的声速范围分别为 1 491.2～1 665.9、1 465.9～1 690.1、1 455.7～1 696.5 和 1 279.0～1 843.7 m/s(图12e～12h)。声速在约32 m深度处开始出现异常升高,这与孤石所在20 m深度相比是滞后的。说明斜向原位纵波测量方法能识别沉积层水平方向上的不均匀性,但当异常地质情况与测点水平距离较大时,识别结果呈现一定的滞后性,后期可以通过数据处理反演孤石真实层位。

两种模型在不同Δh下的声速计算结果均表明:随着Δh的减小,计算声速数据波动加剧,计算结果误差明显增大。推测这是由于Δh越小,声信号到达接收点处的时间差越小,精度要求过高导致声速计算结果误差增大。这说明在实际工程测量中,若时间精度不能保证,加密测量反而可能会放大误差。为优化上述结果,保证空间采样率,同时降低计算误差,自上而下每隔Δh依次取间隔1 m的两个测点数据,根据公式(7)计算得到相应声速结果(图13):分层型沉积层模型测点间距为0.5 和0.2 m,计算声速范围分别为 1 462.5～1 734.5 和1 456.6～1 770.6 m/s;含孤石型沉积层模型测点间距为0.5 和0.2 m,计算声速范围分别为1 469.0～1 679.5 和1 461.5～1 693.8 m/s。与优化前相比,计算误差明显降低,曲线更平滑。将图 13 与图 12b和图 12f对比,发现测点间距小的声速结构更精细,这是由于在相同长度上的测点间距越小,测点数量越多,降低了数据随机误差。

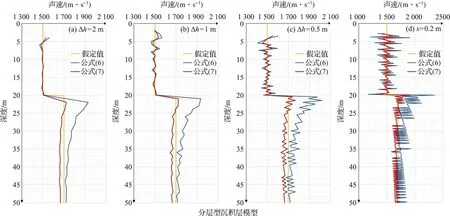
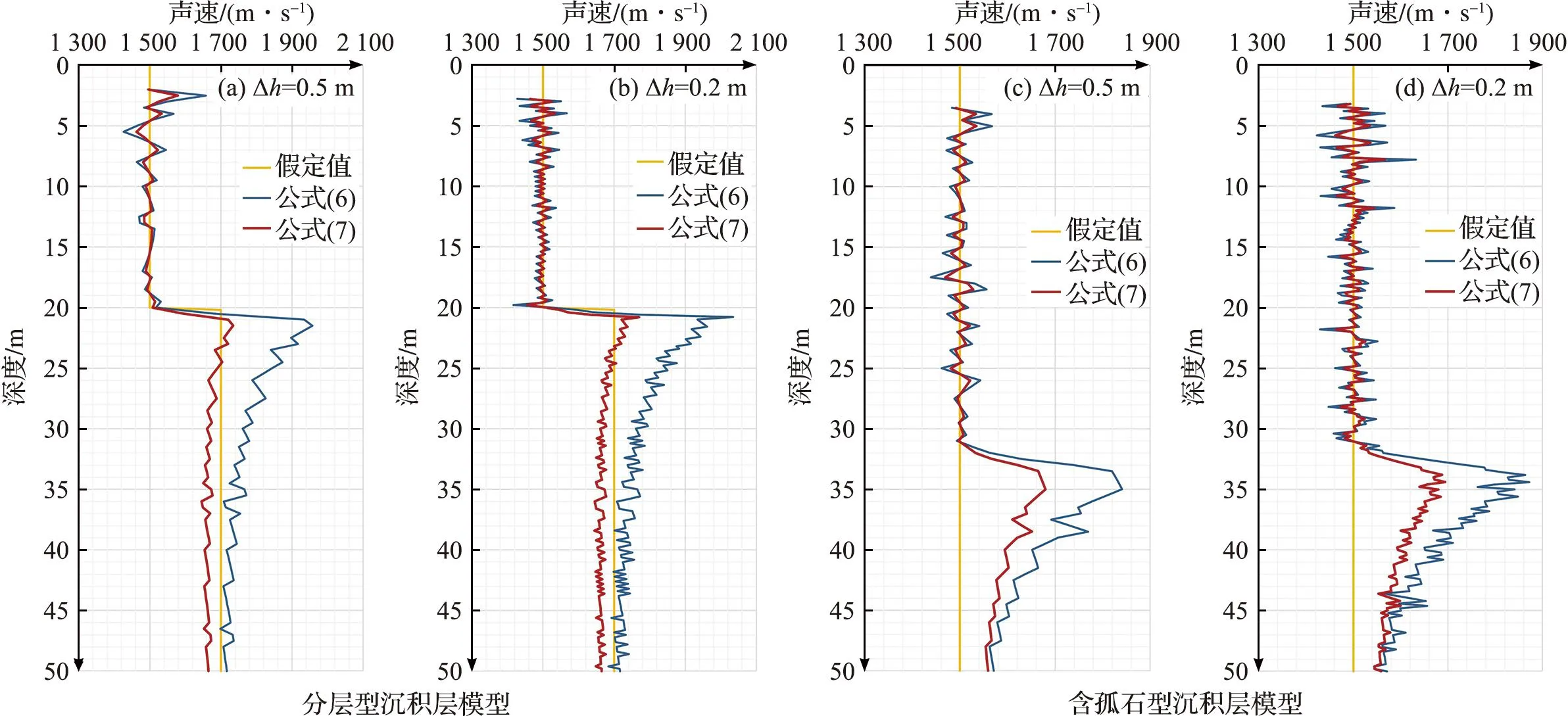
图13 优化后的不同模型在不同测点间距时的声速剖面Fig.13 Optimized acoustic velocity profiles of different models at different measuring point spacing

4 结论与展望

本文提出一种针对海底沉积不均匀性的斜向声学原位纵波测量方法,通过仿真海底沉积层声波传播的瞬态过程,对分层和含孤石两类典型的沉积层不均匀性结构进行仿真,探究发射换能器与接收换能器水平距离、测点间距对于声学原位测量结果的影响,结论如下。

1)沉积层空间结构的不均匀性导致信号异常衰减甚至波形变化,进而对声学特性测量结果产生影响。测点间距Δh越小,获取的沉积层声速剖面结构越精细,但时间精度不够会导致误差放大,增大计算所用测点间隔并对每个测点的结果进行重新计算,可有效减少由于时间测量精度不够带来的误差。

2)斜向测量声源水平偏移距越大,沉积层垂向不均匀性造成的声线弯曲越严重,增大了准确获取沉积层声速剖面的难度,改进后的声速计算公式在一定程度上弥补了斜向测量在准确识别垂向不均匀性方面的不足,后续可考虑进行迭代反演获取沉积层真实声速结构。

3)斜向原位声学探测方法对于沉积空间不均匀性具有良好的识别效果,可广泛应用于海洋工程勘察,服务于海洋工程基础设计,有望在天然气水合物探测及大洋矿产资源调查等领域实现拓展应用。