基于相关性分离的逻辑电路敏感门定位算法

蔡 烁 何辉煌 余 飞 尹来容 刘 洋

①(长沙理工大学计算机与通信工程学院 长沙 410114)

②(长沙理工大学汽车与机械工程学院 长沙 410114)

③(中通服咨询设计研究院有限公司 南京 210019)

1 引言

随着互补金属氧化半导体(Complementary Metal Oxide Semiconductor, CMOS)器件特征尺寸持续缩小，电路规模不断增大，芯片的速度、功耗等性能得到稳步提升。但与此同时，工艺扰动、环境噪声和粒子辐射等造成的芯片失效率问题日益严重，给电路可靠性带来严峻挑战[1-3]，尤其是因空间高能粒子辐射引发的软错误所带来的影响最为严重。依据国际半导体技术发展蓝图(International Technology Roadmap for Semiconductors,ITRS)对集成电路的预测，电路制造工艺由45 ns缩减至12 ns时，电路软错误率可增加10个以上数量级。因此，在设计阶段对电路失效率进行有效评估并采取合理容错与加固设计以提高产品可靠性变得刻不容缓[4]。

电路可靠程度可用电路失效率衡量。准确、高效地评估电路失效率是指导高效容错设计的前提[5]。逻辑电路失效率评估方法一般可分两类：基于模拟的方法与基于信号概率分析的方法。蒙特卡罗(Monte Carlo, MC)方法是典型的基于模拟的方法，其准确性与模拟次数密切相关[6]。由于要模拟多次才能保证准确性，MC方法往往耗时较长。概率转移矩阵(Probability Transition Matrix, PTM)与概率门模型(Probabilistic Gate Models, PGM)方法都可通过准确分析电路的输入输出关系评估电路整体失效率。PTM方法通过建立基本门电路的输入与输出关系评估电路可靠性，是一种能准确计算电路整体失效率的概率分析方法，其缺点是算法的空间复杂度太大[7,8]。PGM方法利用条件概率计算不同类型扇出重汇聚结构的节点信号概率，具有线性的空间复杂度，但在扇出重汇聚处的指数级时间复杂度未能得到有效解决。基于PGM的估算方法则假设所有逻辑门的输入信号相互独立，通过逐个门迭代计算输出节点概率，虽然计算过程简单，但因忽视了信号相关性影响，仅能得到近似结果[9-11]。文献[12]表明三模冗余技术是目前使用最广泛的缓解FPGA软错误的电路加固技术，可以有效提高电路可靠性。文献[13]提出的关键信号算法(Critical Score Algorithm, CSA)可快速计算特定输入下的电路失效率，其复杂度与电路规模呈线性关系，但也因其没有考虑信号相关性而导致准确性不高。当前关于电路信号相关性的研究仍无法做到在保证计算精度的情况下解决耗时问题，难以应用于超大规模电路的评估与计算。

精准定位敏感目标且针对性地容错加固能以最小代价降低电路失效率[14,15]。在容错设计中，人们关注的是那些对电路输出端有直接影响的门，即敏感门。敏感门与输入激励向量及电路拓扑结构有关[16]。文献[17]结合信号传播特点，通过深度优先搜索递归算法对敏感单元进行标识，但因其重复计算扇出节点而影响了准确性。文献[18]考虑了扇出源节点与敏感门的关系，并通过从电路原始输出端向前迭代获取潜在敏感门集合，再逐一验证集合中的门单元。然而，潜在敏感门集获取方法是基于关键信号的，没有准确考虑信号相关性影响的情况下，潜在敏感门集本身存在误差。综上，由于电路规模增大和信号相关性影响，目前的方法很难既准又快地评估超大规模电路失效率[19]；也很难精准、高效地定位对电路失效率影响较大的敏感单元。

本文提出一种相关性分离方法用于准确、快速地计算特定向量激励下的电路失效率；在此基础上，利用相关性分离后的电路模块和反向搜索算法精准定位电路敏感单元；再综合考虑多输入激励的情况，确定最优容错目标，实现以低容错成本提高电路可靠性的目的。

本文第2节详细介绍相关性分离方法(COrrelation SEparation Approach, COSEA)；第3节提出基于相关性分离的逻辑电路敏感门定位算法；第4节对一系列电路的实验结果进行分析；最后是结论。

2 相关性分离方法

本文提出一种充分考虑信号相关性的逻辑电路失效率计算方法，该方法将电路划分为多个独立电路结构(Independent Circuit Structure, ICS)，并以这些独立电路结构为基本计算单元，分析它们的出错率及故障在电路中的传播情况，以此计算电路失效率。下面介绍此方法的原理与计算过程。

2.1 ICS分类与计算

逻辑电路中普遍存在大量扇出重汇聚结构。上游电路的故障信息会在扇出节点处沿扇出分支传播，若扇出支路重汇聚，则汇聚路径包含相关的故障信息，导致信号具有相关性。可在扇出支路上标记故障来源，根据分支标记溯源故障信息。以扇出节点为间隔将电路划分为不同电路模块。每个模块包含多个输入节点和一个输出节点，其中，输入为电路扇出节点或原始输入信号，输出为扇出节点或原始输出。每个电路模块代表的电路结构都不同，模块失效率相互独立，将这些模块称为独立电路结构。根据ICS输出节点的不同，将其分为两类：输出节点为扇出节点的ICS称为扇出相关电路CFR，其对应的失效率PFR通过扇出源传播；输出为非扇出节点的ICS称为扇出无关电路CFI，其失效率PFI表示以该节点为输出的ICS失效率。

对于非扇出节点j，以该节点为输出的ICS类型为CFI，其对应失效率PFI计算如式(1)所示：

其中，t为其关键信号个数，PFIi为第i个关键输入信号的PFI。

实际上，CFI可转化为CFR。转化后CFR的失效率PFR等于转化前PFI的失效率，与此同时，CFI(b)的PFI变为0，计算过程如式(2)所示：

式(2)表明，在检测到b点为扇出节点后，以b点为输出的CFI(b)即转化为CFR(b)。

2.2 节点信息定义与计算

电路节点的出错率受该节点输入锥中逻辑门的影响。将电路划分为不同的CFR和CFI，节点j的出错率可表示为EPNj= function(CFR1, CFR2, ···,CFRm, CFIj)。其中，m为节点j的输入锥中CFR的个数，CFIj为以节点j为输出的CFI。CFIj对节点j的影响是必然的；而对于CFR，其故障可能被屏蔽，也可能被传播至目标节点j，对该节点的出错率产生影响。因此，节点j的出错率EPNj可表示为

其中，nc为对节点j出错率有影响的CFR的数目，PFRj为CFRj的失效率，PFIj为CFIj的失效率。

影响目标节点出错率的CFR可能有多个，用U表示影响该节点的CFR集合；影响目标节点的CFI只有一个。通过以下节点信息可计算整个电路失效率：节点逻辑值LV、节点PFI、影响节点出错率的CFR集合U。T表示此3类信息集合，即T={LV, PFI,U}。节点逻辑值LV由门输入信号和门类型决定；PFI可利用CSA方法计算，随着目标节点的变化，CFI可转化为CFR。

接下来介绍如何计算集合U。CFR的故障信息通过其输出节点(扇出源)传播，当扇出分支在同一节点汇聚，由于故障信息已保存，在计算该节点出错率时可充分考虑到CFR间的相关性。目标节点前驱逻辑门的输入信号中，若多个输入信号中存在相同的CFR，则说明它们源于同一个CFR。

图1描述了n输入与门输出节点的CFR集合U的计算过程。设与门输入信号中‘1’的个数为n1，‘0’的个数为n0，n1+n0= n。输入为‘1’的信号记为P1，P2, ···,Pn1，对应节点信息为{TP1,TP2, ···,TPn1}，其中TPi={LVPi, PFIPi,UPi}；输入为‘0’的信号记为Q1, Q2, ···,Qn0，对应节点信息为{TQ1,TQ2, ···,TQn0}，其中，TQi={LVQi, PFIQi,UQi}。第Pi个‘1’信号节点信息的CFR集合UPi= {CFRPi(1),CFRPi(2), ···, CFRPi(kPi)}，第Qi个‘0’信号节点信息的CFR集合UQi= {CFRQi(1), CFRQi(2), ···, CFRQi(kQi)}，图1中各信号线上所列即为输入信号所对应的U。输出端的节点信息Tout= {LVout, PFIout, Uout}。

图1 与门输出节点的集合U计算过程

针对不同输入，分情况讨论输出节点的CFR集合U的计算方法，表1列出了与门输出节点信息。同理，或门及非门的输出节点信息的计算方法与门类似，不再赘述。

表1 与门输出节点信息

(1) n1= n, n0= 0。如图1(a)所示，与门的所有输入都为1，其正常输出为1。此时，任意输入信号的CFR出错，都将导致与门输出出错。因此，输出节点的U即为输入节点的U之并集，即Uout=；

(2) n1= n-1, n0= 1。如图1(b)所示，与门输入中存在一个0信号，其正常输出为0。输入信号Qi上的CFRQi(kQi)出错，将导致与门输出出错；但若CFRQi(kQi)也存在于其他输入1信号中，则CFRQi(kQi)出错将使输入1信号变为0，导致与门输出仍为0。因此，只有存在于输入0且不存在于任意输入1上的CFR出错，才会导致与门输出出错。此时，输出节点的U为输入0信号的U减去所有输入1信号的U之并集，即

(3) 1＜n0＜n, n1=n-n0。如图1(c)所示，与门输入中存在多个0 信号，其正常输出为0。与图1(b)情形类似，只有存在于所有输入0信号且不存在于任意输入1信号上的CFR出错，才能导致门输出出错。所以输出节点的U为所有输入0信号的U 之交集减去所有输入1 信号的U 之并集，即

3 敏感门定位算法

敏感门(Critical Gates, CG)指那些若发生故障便将直接导致电路失效的逻辑门。CG的故障不会被下游电路逻辑屏蔽，而是被传至电路原始输出端，或被下游存储单元捕获，从而导致电路失效。本节提出基于COSEA的敏感门定位算法，包括单个输入向量激励下电路的敏感门定位方法和多输入向量激励的敏感门定位方法(Vector Critical Gate Location Algorithm, VCGLA)。

3.1 向量敏感门定位算法

在单个特定向量激励下，若逻辑门故障导致电路失效，则称此逻辑门为向量敏感门(Vector Critical Gate, VCG)。对特定电路而言，不同输入向量对应不同的VCG集合。本节介绍如何计算电路的VCG集合。

类似地，将那些若发生故障便会导致电路失效的ICS称为敏感ICS，否则为非敏感ICS。显然，所有以电路原始输出节点为输出的CFI都是敏感ICS。电路中的CFR是否为敏感ICS则取决于电路的拓扑结构和当前输入向量。由于非敏感ICS的故障不会导致电路失效，所以该结构内部的逻辑门都不是向量敏感门；而敏感ICS结构内部的逻辑门也并非都是向量敏感门，可使用关键信号定位敏感ICS内部的向量敏感门。

VCGLA首先对输入的电路网表进行解析，针对每个单独的输入向量调用COSEA计算电路所有原始输出的节点信息T；其次，对所有输出节点的集合U进行分类，得到对电路输出有影响的敏感ICS集合；最后，对得到的ICS进行敏感门定位，使用反向搜索算法从ICS的输出向上游迭代，通过关键信号定位每个能影响到此ICS输出的逻辑门，将它们加入至敏感门集合。具体过程如算法1所示。

3.2 示例说明

本文以图2电路为例说明VCGLA具体计算过程。

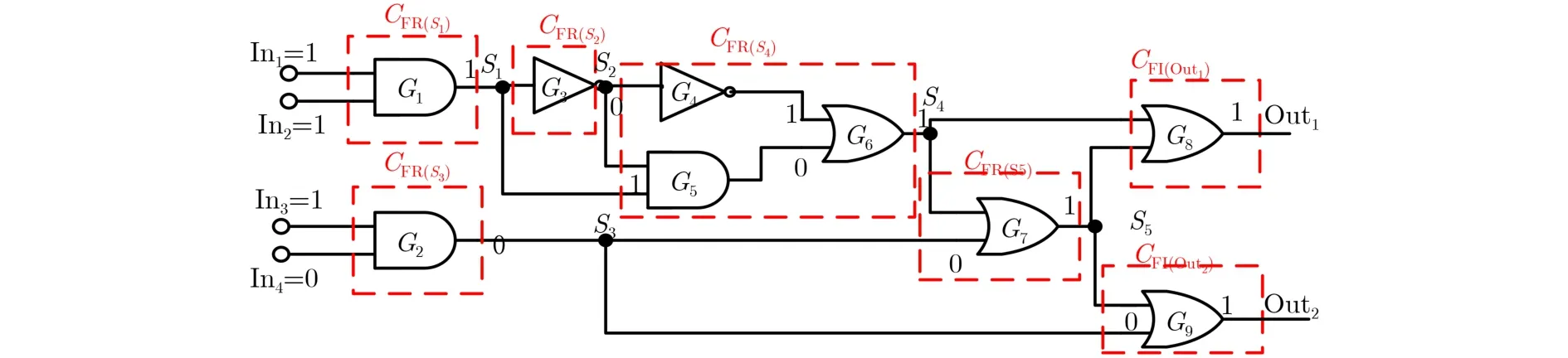
图2 示例电路

步骤1 根据COSEA方法计算示例电路原始输出Out1和Out2的节点信息分别为Tout1={1, FPG,{CFR(S1), CFR(S4)}}和Tout2={1, 4FPG, {CFR(S1),CFR(S4), CFR(S5)}}，则输出节点的UCFR= Uout1∪Uout2= {CFR(S1), CFR(S4), CFR(S5)}, UCFI= {CFI(out1),CFI(out2)}。电路节点信息的具体计算过程如表2所示，其中No表示该节点处不需要进行CFI和CFR之间的转化。

算法1 VCGLA算法

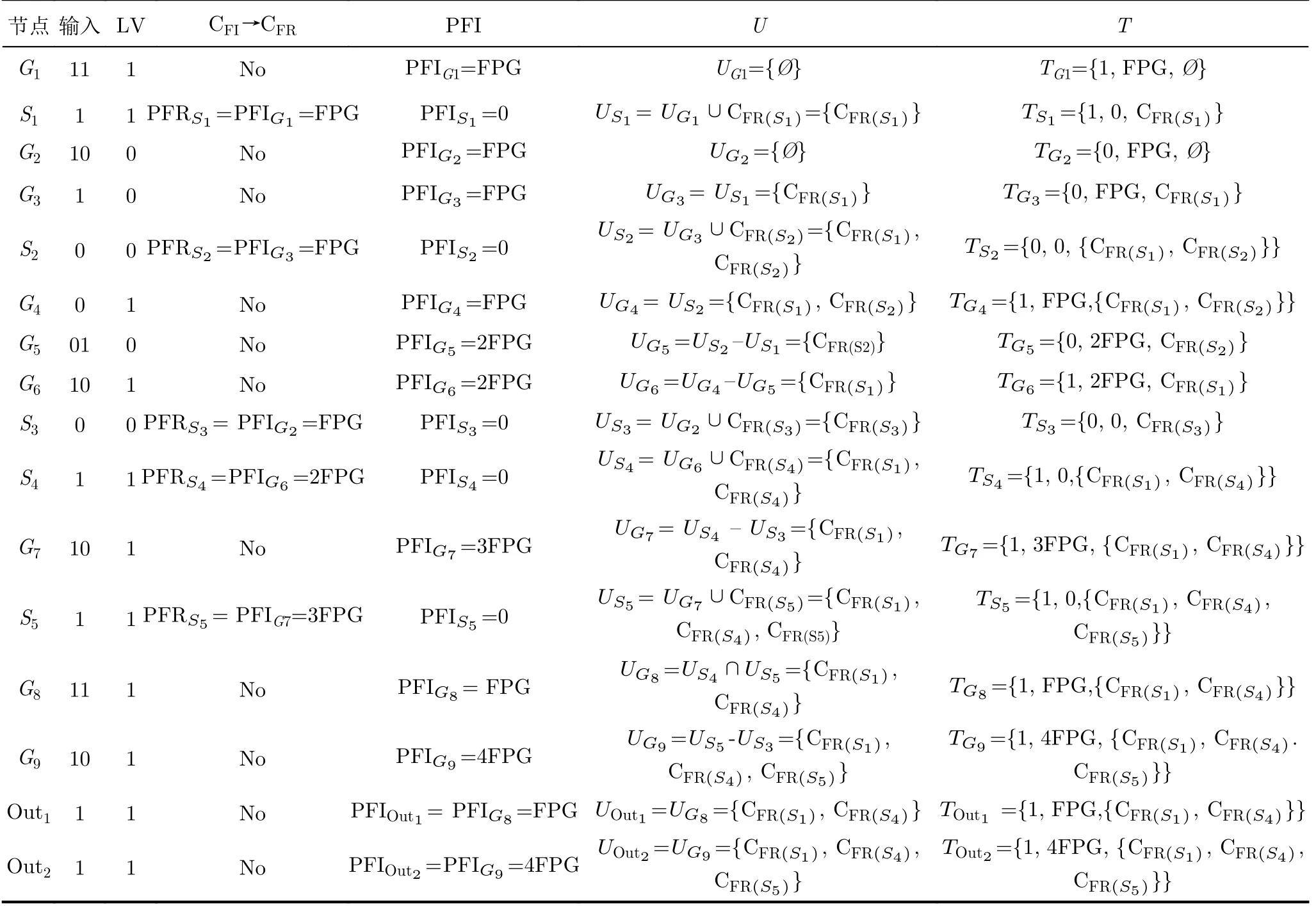
表2 示例电路节点信息计算过程

步骤2：定位每个敏感ICS内的向量敏感门，在此以CFR(S4)为例。CFR(S4)为UCFR中的敏感ICS，首先找到输出节点G6，将G6加入向量敏感门集合；然后，向前追溯G6的输入信号“10”，由于G6是或门，所以输入‘1’为G6的关键信号，该信号的前驱逻辑门为G4，故将G4添加至向量敏感门集合；最后，G4的前驱为扇出节点S2，停止此次迭代。因此，CFR(S4)的向量敏感门为G4和G6。分析所有敏感ICS可知，在输入向量为“1 110”时，电路的向量敏感门集合为{G1, G4, G6, G7, G8, G9}。

3.3 电路敏感门定位算法

电路中被多数向量甚至所有向量都定位为向量敏感门的逻辑门，被称为电路敏感门(Circuit Critical Gate, CCG)，它们是容错设计的重点，对该部分逻辑门进行容错，能够大幅度提高电路可靠性。本节我们提出一种电路敏感门定位算法(Circuit Critical Gate Location Algorithm, CCGLA)，如算法2所示。

若逻辑门G为输入向量V的向量敏感门，则向量V为逻辑门G的敏感向量。定义逻辑门的敏感向量数占总输入向量空间的比值为该逻辑门的敏感度GS。设定敏感度阈值Th，认为电路敏感门即电路中敏感度超过阈值Th的逻辑门。例如，某电路的原始输入数为w，其输入向量空间大小为2w。计算所有输入向量空间的敏感门集合分别为VCG1,VCG2, ···, VCG2w，若逻辑门Gi出现在其中ki个向量敏感门集合中，则Gi的敏感度为ki/2w。随着输入数和电路规模的增大，计算所有输入向量的敏感门集合变得非常困难，因此，通常只选取部分向量计算对应敏感门。设N为选取的向量个数，ki为第i个逻辑门Gi的敏感向量数，则Gi的敏感度为

算法2为CCGLA算法总体框架，包含3步：(1)选取N个向量，计算这些向量对应的向量敏感门集合：VCG1, VCG2, ···, VCGN；(2)计算电路中每一个逻辑门的敏感度；(3)设定阈值参数Th，比较逻辑门的敏感度与阈值Th的大小，超过阈值的门添加至电路敏感门集合。

4 实验结果及分析

4.1 VCGLA效果验证

模拟实验在配备3.0 GHz微处理器和8 GB内存的计算机上进行。VCGLA, CCGLA和CGC方法都是基于MATLAB 2014a平台。ISCAS-85,89系列电路应用于文献[16-18,20]进一步验证提出的方法的准确性，其中文献[17,18]提出的CGC方法被广泛应用于电路敏感门定位，通过与其对比验证VCGLA的准确性与高效性。其中，CGC的变体方法共有6种，选取实验条件相似(单线程)的CGC-V1, V3,V4和V6方法进行对比。V1方法通过逐个检测电路每个单元的敏感性获取向量敏感门，准确率为100%，但因为对每个逻辑门进行检测耗时太高，无法用于大规模和超大规模电路的敏感门定位；相比之下，V3方法是一种快速的VCG定位方法，但准确性不高。V4和V6方法的准确性与定位速度介于以上两种方法之间。

算法2 CCGLA算法

考虑到CGC-V1, V4和V6方法所需时间较长，针对实验电路的每种方法各选择100个向量，用于定位电路的VCG集合。本实验中，由于CGC-V1方法能精准定位VCG集合，故以其为标准验证其他方法的准确性。针对ISCAS’85系列4个规模较小的电路，表3列举了VCGLA与CGC-V1, V3, V4和V6方法的比较结果。其中，avg.CG为100个相同随机向量激励下对应的敏感门数目的平均值，avg.err是它们与CGC-V1方法相比的误差平均值(即每个向量对应VCG误差的平均值)，如式(5)所示，max.err表示单个随机向量激励下敏感门集合误差的最大值，如式(6)所示，表3还列出了单个向量激励下定位对应VCG的平均计算时间。

表3 VCGLA与CGC-V1, V3, V4和V6方法的比较

其中，m1是是激励向量数，VCGCGC-V1(i)是由CGC-V1方法定位出的第i个输入向量的VCG,VCGOther(i)表示其他几类方法计算出的第i个输入向量的VCG，在此统一表示。公式中的VCG差值实际是两个集合中不同的敏感门总数：相比CGCV1方法定位的VCG集合，用其他方法定位的VCG集合中漏检与误检的敏感门。

表3中VCGLA的max.err列都为0表明VCGLA与CGC-V1方法找到的所有敏感门集合完全相同，表明本方法在定位向量敏感门时具有100%的准确性；而在定位速度上，VCGLA平均耗时0.2 s，相比CGC-V1的537.3 s快了3个数量级以上。CGCV3是唯一一个在定位速度上稍快于VCGLA的方法，但由它定位的敏感门集合的最大误差平均值为69.5，且平均误差为22.8，是所列方法中准确性最低的。CGC-V4和V6的速度和准确性介于CGCV1和V3之间，但都不及VCGLA。相关性分离方法通过将电路划分为多个ICS，再以ICS为基本单元分析故障传播及信号相关性影响，在保证准确性的前提下，大大简化了敏感门定位算法的迭代过程。

接下来使用VCGLA计算更大规模电路，衡量其计算大规模和超大规模电路时的有效性，结果如表4所示。考虑到CGC-V1, V4和V6方法的计算时间太长，已很难在合适的时间内定位这些大规模电路的敏感门，后续实验中我们仅使用VCGLA与CGC-V3方法定位敏感门。在表3和表4中，avg.err和max.err的含义相同，都是以CGC-V1方法结果为参考。只是表4中计算avg.err和max.err时，使用VCGLA方法的计算结果代替了CGC-V1方法结果，因为之前已证明，VCGLA方法与CGC-V1方法结果一致，且速度远快于后者。所选实验电路包括ISCAS’85, 89系列和ITC’99的10个电路。对于其中规模相对较小的电路，各选取10 000个测试向量，随着电路规模的不断增大，考虑到定位时间的快速增长，所选取向量的数目逐渐减小。

表4 VCGLA与CGC-V3方法定位大规模电路的敏感门

从表4可知，电路规模达到万门以上，VCGLA的计算耗时仍与CGC-V3方法相差不大，二者计算超大规模电路的向量敏感门速度都比较快。在实验中，随着电路规模的增长，VCGLA方法的计算耗时基本随逻辑门的数量呈线性增长，充分证明所提算法的可拓展性。因此，VCGLA可应用于更大规模电路的敏感门精准定位。

4.2 CCGLA效果验证

影响电路敏感门(CCG)定位性能的参数包括选取的向量数N和敏感度阈值Th。先考虑N的变化对CCGLA的影响。实验电路选取C7552的一个单输出子电路，输出节点编号为65。实验使用CCGLA计算当N为不同值时该子电路的敏感门集合，且对设定的每个N值，取Th的范围为0～1，步长为0.05。以N=50 000时的计算结果为参考标准，比较N取其它值时对应21个不同Th的电路敏感门集合，并将此21组差值求和表示为该N值与最大N值(N=50 000)的敏感门集合差，实验结果如图3所示。由图可知，当N＜5 000时，对应电路敏感门集合与参考标准差别逐渐减小；当N＞5 000时，随着N继续增大，敏感门集合差异已可忽略。实验说明，当N增大到一定程度即可用于准确定位CCG集合，无需遍历所有输入激励。实际上，对多数电路都有此结论。

图3 N的变化对敏感门差异的影响

Th是电路敏感度阈值，其值可影响CCG集的大小和质量：Th值若增大，则CCG集合中的元素减少，但CCG的敏感度更高；反之，则CCG数增加，但门的敏感度降低。定位CCG的目的是更高效地对电路进行容错加固。在此，假设改进后的CCG无错，对比容错前后的电路失效率，即可得到对该CCG集合容错后电路失效率的改善情况，以此评估Th对CCG定位及容错效果的影响。为保证失效率计算结果的准确性，使用MC模拟方法计算容错前后电路的失效率，模拟次数为5×106。实验电路为ISCAS’89系列电路。

本实验分5步：(1)选定实验电路，使用MC方法计算实验电路失效率，将逻辑门的出错概率设为10-4[15,20]；(2)设N=10 000，针对Th值定位CCG集合；(3)计算容错后电路失效率，并对比容错前电路失效率；(4)改变Th大小，其范围为0～1，间隔步长为0.05；(5)重复步骤(3)和步骤(4)，分析Th对容错效果的影响。

实验结果如图4所示，图4(a)-4(f)分别描述不同电路下Th变化对电路失效率的影响。蓝色折线为针对不同Th值定位CCG集合并容错后得到的电路失效率；绿色直线为不进行容错的电路失效率。在图中，当Th为0时，所有输入激励对应的CCG都是容错对象，容错后电路失效率最低(可认为是0)；随着Th增大，容错对象减少，容错后电路失效率也逐渐增大；当Th为1时，只有极少数CCG为容错对象，容错后电路失效率最高。

图4 敏感门容错前后电路失效率对比

容错效果与容错代价是需综合考虑的两个重要指标。设FPCa和FPCb分别为容错后和容错前电路失效率，两者之间的改善比率定义为电路失效率改善率(Improvement Rate of Failure, IRF)，如式(7)所示；NCCG为CCG集合的元素个数，NCCG与电路总门数Num的比值称为电路敏感度比值(Circuit Critical Gate Rate, CCGR)，如式(8)所示。容错效果可用IRF衡量，IRF越大，说明容错效果越好；容错代价则用CCGR衡量，CCGR越小，则表明容错代价越小。定义容错效率(Fault Tolerance Efficiency, FTE)为IRF和CCGR的比值，如式(9)所示。FTE越大，表示对CCG集合容错的效率越高。

图5中两条曲线分别描述了所选择的6个实验电路的IRF和CCGR随Th的变化情况，其中蓝色折线代表IRF，绿色折线代表CCGR。由图可知，IRF与CCGR都随Th的增大而减小。当电路设计人员以特定的IRF为电路设计目标时，可根据IRF选择Th值，从而得到对应的CCG集合，再对集合中的逻辑门进行容错；当以特定的CCGR为电路容错限制条件时，同样可选择对应Th值以得到CCG集合，再进行容错处理。

图6为实验电路的FTE随Th的变化情况。当Th为0时，FTE最小，随着Th增大，FTE也逐渐增大；当Th增大到一定程度时，FTE的增大开始变缓，甚至有减小趋势。从本文实验电路的结果可知：当Th为0.6～1的范围时，电路容错效率较高，但不同电路最佳容错点对应的Th会有差别。

图6 FTE随Th的变化

5 结论

本文提出了一种基于相关性分离的逻辑电路敏感门定位算法。首先将整个电路分离成多个独立电路结构；再针对独立电路结构反向搜索定位特定输入向量的向量敏感门；最后进一步定位面向向量空间的电路敏感门。使用本文提出的敏感门定位算法，能精准定位对多数输入激励都敏感的逻辑门集合；而针对这些敏感门进行容错加固将有助于提升整个电路可靠性，同时能保证较低的容错开销。相比于其他敏感门定位算法，本文提出的算法既准确又高效，适用于定位大规模及超大规模电路的敏感门单元，以辅助高效容错设计。