重叠阵元时分复用MIMO雷达多目标参数估计方法研究

田 丰 刘 万 符渭波② 张浩宇

①(西安科技大学通信与信息工程学院 西安 710054)

②(西安市网络融合通信重点实验室 西安 710054)

1 引言

交通流量监测是现代城市道路、高速公路和智能交通系统的重要组成部分，毫米波雷达具有抗干扰强、分辨率高、成本低等优势，时分复用多输入多输出(Time Division Multiplexing Multi-Input-Multiple-Output, TDM-MIMO)体制毫米波雷达已是交通流量监测的主要雷达方式，但多普勒-角度会产生耦合影响运动目标角度估计的精度，测速范围不满足实际探测需求。因此，开展多普勒-角度耦合和速度解模糊问题的研究，对提高交通流量监测精度具有十分重要的意义[1-3]。

针对多普勒-角度耦合问题，Hu等人[4]提出一种稀疏重构(Sparse Reconstruction, SR)技术和随机传输方案重建目标的多普勒频谱实现运动补偿，在该方法中速度与角度是独立估计的。Bechter等人[5]引入了距离多普勒处理，以减小TDM-MIMO雷达中因目标运动引起的相位误差。Lin等人[6]通过对参考阵元的接收信号进行处理，提取目标运动引入的相位差，进而对阵列进行运动补偿。Hu等人[7]提出一种新的线性调频序列，消除了多普勒-角度耦合问题。Häfner等人[8]提出一种基于模型的估计方法，实现角度-多普勒耦合补偿和多普勒带宽恢复。Neemat等人[9]提出了一种新的波形和处理方法，利用差拍频率信号复用的方法避免了多普勒-角度耦合问题。Jung等人[10]通过在距离-速度检测结果中比较和排列同一目标对应的信号相位，可以估计目标的明确速度和角度。Nguyen等人[11]提出了一种利用距离分多址(Range Division Multiple Access,RDMA)和多普勒分多址(Doppler Division Multiple Access, DDMA)实现调频连续波雷达多输入多输出(Multiple Input Multiple Output, MIMO)功能的方法。

针对速度模糊问题，王元恺等人[12]通过在扫频周期前插入延时，利用相位差信息解多普勒模糊。周奇特等人[13]提出了一种改进的脉冲相干多普勒测速的速度模糊消除方法，通过“相关-相位”组合法进行精确时延估计。Xu等人[14]通过引入距离多普勒处理(Doppler-Range Processing, DRP)算法解决速度模糊问题。Scherhäufl等人[15]提出一种利用维特比译码器解决相位模糊问题的方法。Gonzalez等人[16]通过引入基于密度的聚类(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)算法改进了中国剩余定理速度解模糊算法，实现速度解模糊。Baral等人[17]提出了一种新的代价函数，通过恢复减少的无模糊多普勒频谱间隔来联合估计每个目标的多普勒频率和波达方向(Direction Of Arrival, DOA)。Xiong等人[18]提出了一种基于宽带雷达回波时延互相关处理的距离扩展目标微多普勒模糊度检测方法，将信号的微多普勒频率降低到适当的数值。王超等人[19]提出一种基于回波序列最小二乘拟合的速度估计方法，可以得到目标速度并有效避免速度模糊。

虽然现有方法在理论上一定程度解决了多目标的速度模糊和多普勒-角度耦合问题，但在实际复杂交通场景中，其估计精度往往会大幅降低。本文将通过优化MIMO雷达阵列天线布局，使虚拟阵元在空间上形成重叠，采用重叠阵元特性补偿相位偏移，并通过迭代方式校正阵元间位置误差，实现目标角度估计；通过重叠阵元间的相位差和模糊速度相结合的方式解速度模糊，采用频谱搬移方法解决速度跳变问题。

2 基于重叠阵元的运动补偿和速度解模糊方法研究

2.1 基于重叠阵元的天线阵列结构设计

发射阵列设计为M元均匀线阵，发射阵元之间的间距为Td=dN/2。接收阵列均分为两部分，左侧由接收阵元1～N/2构成，阵元间距为Rd1=d，右侧由接收阵元N/2+1～N构成，阵元间距为Rd1=d，接收阵元N/2和N/2+1之间的阵元间距Rd2=[(M-1)N/2-1]d。基于以上天线阵列形成的等效虚拟接收阵列是由M×N-2个虚拟阵元构成的均匀线阵，阵元间距d=λ/2(λ是自由空间波长)，其中第1个发射阵元发射第N/2+1,N/2+2个接收阵元接收与第M个发射阵元发射第N/2-1,N/2个接收阵元接收的两对重叠阵元的相位中心重合。MIMO天线阵列和等效虚拟接收阵列图如图1所示。

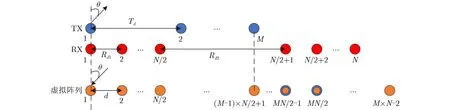
图1 重叠阵元MIMO天线阵列

发射天线的发射顺序按照TX1, TXM, TX2,···,TXM-1的顺序发射，从TX1发射开始到TXM-1发射结束为一个MIMO周期。TDM-MIMO发射波形图如图2所示。

图2 TDM-MIMO发射波形

假设空间中存在1个远场目标，无噪声的环境下，锯齿波发射信号在第k个调频周期表示为

其中，A为发射信号振幅，f0为初始频率，φ0为初始相位，µ为调制斜率

其中，T为线性调频调制周期，B为调频带宽。

发射信号经过目标反射，接收天线接收到回波信号SR(t)，其中由于目标距离、目标速度和天线阵列间距的影响，回波信号相对于发射信号会产生3部分时延：目标相对于雷达径向距离造成的时延ΔtR、目标相对于雷达径向速度造成的时延Δtv和天线阵列间距造成的时延Δtant。

为了获得目标距离、速度和角度信息，需要对回波信号进行信息提取。将回波信号与发射信号混频，得到包含单频和高频的混合信号，其中速度和距离信息包含在单频信号中，高频信号为非单频信号，且远远大于单频信号的频率，所以通过低通滤波器滤除后得到差拍信号。第1个虚拟阵元接收的差拍信号为

其中，A1表示回波信号幅度。第n个虚拟阵元接收的差拍信号表示为

其中，φn表示第n个虚拟阵元的相位信息。

采用4发4收的天线阵列，即M=4,N=4，天线阵列排布方式采用图1所示结构。假设每个周期的信号幅度相等，以第1个虚拟阵元为参考阵元，第n个虚拟阵元的相位φn表示为

其中，φd=2πf0Δtant=2πdsinθ/λ表示电磁波在相邻阵元之间传播路径对应的相位差；φv=2πfdT表示目标运动在相邻阵元之间引入的相位差，其中fd=2v/λ表示目标运动的多普勒频率。

式(5)中，在第7个和第8个阵元位置形成了重叠阵元。多普勒频移在不同发射天线切换时间内带来的相位变化量φv耦合到接收天线中，造成天线间的相位差φn产生误差，因此需要对多普勒频偏进行补偿。

2.2 基于重叠阵元的运动补偿

基于优化阵列进行角度估计时，多普勒频率会耦合到阵列相位中，造成角度估计错误。由式(5)可知天线阵列中第7个虚拟阵元为第1对重叠阵元对，第8个虚拟阵元为第2对重叠阵元对，假设两对重叠阵元间的相位差分别为φO1和φO2，则第1对和第2对重叠阵元间的相位差表示为

两对重叠阵元间的相位差即运动目标产生的相位差，利用重叠阵元间的相位差估计出相位补偿项φv。通过角反射器等强反射物对雷达进行标定，确定一个补偿的幅相系数，从而保证测角的准确性。因此，除重叠阵元外的阵元位置误差对测角的影响可以忽略。假设第1对和第2对重叠阵元位置误差分别为Δd1和Δd2，位置误差引起的相位变化量分别为φref1和φref2，阵元位置误差与相位变化量关系表示为

其中θ为目标角度，由式(7)可以看出，阵元位置误差与相位变化量呈正相关，而且相位变化量还受目标角度影响。此时两对重叠阵元间的相位差可以表示为

式(6)和式(8)对比可知，重叠阵元位置误差影响了多普勒频率的估计，需对阵元位置误差进行校正。

对多个静止目标数据进行测量，采集不同角度θi(i=1,2,...)的雷达回波数据，进行距离维和速度维FFT后，获取重叠阵元间的相位差，静止目标运动引入的相位差φv为0，则重叠阵元间相位差为

将式(9)代入式(7)，因为θi已知，通过多组数据测量求得重叠阵元间的位置误差Δd1和Δd2。假设16个虚拟阵元对应的目标距离维和速度维FFT结果序列为X(mTX,mRX)，其中mTX(mTX=1,2,3,4)表示发射天线编号，mRX(mRX=1,2,3,4)表示接收天线编号，对2维FFT结果进行相位补偿，补偿结果表示为

相位补偿后，每个有效目标去掉2个重叠阵元的数据，在剩余14个2D-FFT频谱中提取峰值单元，经过重新排列，虚拟阵元的相位φn表示为

2.3 基于重叠阵元相位差的速度解模糊

为了解决TDM-MIMO体制下的速度模糊问题，需要将最大不模糊速度恢复到SIMO体制的速度区间。基于优化阵列的重叠阵元间相位差求多普勒频率，可以得到目标的粗估计速度，结合目标的模糊速度实现速度解模糊。当目标速度接近速度区间边界时，会出现速度跳变现象，即模糊数估计错误。针对速度跳变问题，通过频谱搬移的方式将目标速度估计值搬移到速度区间中心位置，从而防止速度跳变现象的发生。TDM-MIMO雷达的最大不模糊速度为

由式(13)可知，雷达可探测的最大不模糊速度范围为[-vmax,vmax]，相对于SIMO体制雷达最大不模糊速度范围缩小M倍，为了解决TDM的限制，需要将多普勒频率变化范围变为|fv|＜1/2T。通过变换发射时序的方式，构成重叠阵元的发射天线依次发射，重叠阵元间多普勒相位范围为[-π,π]，得到相应的速度区间|v|＜λ/4T。速度模糊模型如图3所示。

图3 速度模糊模型

图3中，雷达采用TDM发射方式时，测速范围在模糊数q=0速度区间内，即速度区间[-vmax,vmax]。利用重叠阵元间相位差得到的目标速度在模糊数q=-M/2～M/2的速度区间内。但是由于重叠阵元间相位误差，速度测量会存在一定误差，所以采用粗估计和精估计相结合的方式进行速度解模糊。

以最大不模糊范围作为一个速度区间[-vmax,vmax]，将速度测量转换为速度区间的确定和区间内速度的精确估计问题，通过运动目标的补偿相位，可粗略估计出目标的速度，确定目标速度区间，利用2DFFT算法对速度区间内速度的精确估计，最终实现速度的解模糊。目标实际速度和雷达估计速度的关系为

其中，vest为速度精估计值，q为速度区间即模糊数。通过式(8)得到运动目标的相位补偿值为φv=φO1-φref1或φv=φO2-φref2，又已知φv=2πfdT，所以目标粗估计速度为

通过v判断目标速度的区间，图3可得速度区间为q。对每个虚拟阵元的差拍信号进行距离维FFT和速度维FFT，得到距离速度频谱图，通过CFAR算法进行目标检测，获得目标的距离和模糊速度vest，即速度的精估计。将粗估计速度v和2D-FFT算法提取的精估计速度vest代入式(14)，得到目标的估计速度vr。

在速度解模糊的过程中，由于粗估计速度由重叠阵元间相位差决定，这就导致粗估计速度相较于真实速度存在一个误差σ，一般情况下σ=vmax，所以不会对模糊区间的确定造成影响。但是当目标实际速度接近速度区间边界值时，误差σ的存在会导致粗估计速度从一个速度区间跳变到另一个速度区间，从而导致速度的测量结果出现接近2vmax速度跳变误差。假设一个待检测速度位于vmax附近，由于粗估计速度误差σ的存在，受到速度跳变的影响，测量结果为vr=vest+2(q+1)vmax。通过对速度区间进行频谱搬移将速度区间由[-vmax,vmax]变为[0,2vmax]，搬移后的速度模糊模型如图4所示。

图4 搬移后的速度模糊模型

经过速度解模糊后，雷达的不模糊速度区间变为[-Mvmax,Mvmax]，恢复到信号时分复用前的范围，此时的不模糊速度区间满足实际要求。

2.4 运动补偿和速度解模糊算法设计

基于重叠阵元的MIMO雷达运动补偿和速度解模糊方法主要分为目标检测、运动补偿和速度解模糊3个部分，运动补偿算法和速度解模糊算法流程图如图5所示。

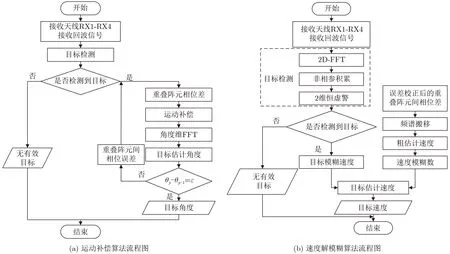
图5 算法流程图

3 仿真与实测结果分析

实测中，雷达探测距离应大于 200 m，探测速度应大于120 km/h，发射波束能完全覆盖单向或双向 4 车道的探测范围。雷达天线阵列采用4个发射天线和4个接收天线，其中包含2对重叠阵元，阵元间距设定为d=1.5λ，阵列布局如图1所示结构。实际场景为多目标场景，因此雷达信号波形采用锯齿波调制的调频连续波，发射天线按照TX1, TX4,TX2, TX3顺序发射信号，接收天线同时接收回波信号，利用本算法对回波信号进行处理，毫米波雷达参数如表1所示。

表1 毫米波雷达参数

3.1 仿真分析

设置3个不同运动状态的目标进行参数估计来验证算法有效性，模拟目标参数如表2所示。

表2 模拟目标参数

对接收天线的回波信号进行处理。通过2D-FFT对差拍信号进行信息提取，得到关于速度和距离的频谱图，取1个MIMO周期中的第1个接收天线的信号进行结果分析，2维频谱图如图6所示。

图6 2维频谱图

图6(a)和图6(b)中包含3个峰值分别对应3个目标，通过峰值对应的坐标可以获得3个目标的距离和模糊速度。第1个目标的距离测量值和速度测量值分别为18 m和4.99 m/s，与目标的真实距离18 m和真实速度5 m/s吻合；第2个目标的距离测量值为34.5 m，与目标的真实距离35 m吻合，速度测量值为1.19 m/s，与目标实际速度15 m/s相差13.81 m/s，因两者速度误差较大，所以目标2存在速度模糊；第3个目标的距离测量值为90.5 m，与目标的真实距离90 m吻合，速度测量值为7.70 m/s，与目标实际速度-20 m/s相差27.7 m/s，所以目标3存在速度模糊。图6(c)中目标2和目标3的实际速度分别在模糊数为1和-2的速度区间内，结合模糊数和模糊速度得到目标2, 3的速度分别为15.08 m/s和-20.07 m/s，与实际速度相差0.08m/s和0.07 m/s，速度估计结果基本吻合，具体仿真结果如表3所示。

表3 多目标仿真结果

为了验证基于重叠阵元解模糊算法的抗噪性，在目标对应的中频信号中添加不同信噪比(Signal to Noise Ratio, SNR)的噪声，采用蒙特卡罗仿真方法统计不同信噪比条件下速度解模糊的正确率。基于重叠阵元天线阵列，对比本文速度解模糊算法与重频参差速度解模糊算法的抗噪性。当目标的解模糊速度与真实速度的误差小于1 m/s时，认定速度解模糊正确。解模糊算法性能如图7所示。

图7 速度解模糊算法性能

图7(a)表明，随着信噪比的增加，速度解模糊的正确率逐渐提高，当信噪比为-20 dB时，速度解模糊正确率为1，随着信噪比的增加，正确率始终为1。当信噪比为-6 dB时，重频参差算法正确率为1。本方法正确率一直高于重频参差算法，并且解模糊正确率最先趋于1。图7(b)表明，随着信噪比的增加，速度均方根误差逐渐减小，当信噪比为-20 dB时，解模糊正确率为1，速度均方根误差为0.11 m/s，当信噪比大于-20 dB时，速度均方根误差保持在0.11 m/s。本算法在低信噪比环境下仍能有效解决速度模糊问题。

为了验证运动补偿方法的有效性，在考虑阵元位置误差的前提下，仿真1TX-14RX的SIMO雷达系统和基于多普勒频率相位的运动补偿方法，并分别与本方法进行对比。选取目标3的角度波形图进行结果分析，目标3的角度波形图如图8所示。

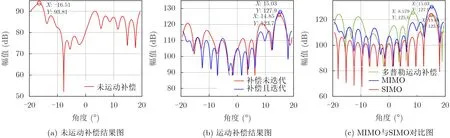
图8 目标3的角度波形图

图8(a)为单目标未进行运动补偿的角度波形图，会出现目标角度估计偏差较大或一个目标被判断为多个目标的现象；图8(b)为运动补偿后的角度波形图，其中红色曲线表示仅对阵列相位进行运动补偿的角度波形图，蓝色曲线表示对阵列相位进行运动补偿并迭代校正的角度波形图。未迭代角度峰值为14.85°，与实际角度15°相比存在一定的偏差，副瓣偏高，而且随着目标角度的增大误差逐渐增大；经过迭代后的角度峰值为15.03°，与实际角度相吻合。运动补偿后可以估计出目标角度，但是阵元间位置误差会影响测角精度，通过迭代算法可以提高角度测量精度。图8(c)为本方法MIMO体制与SIMO体制的对比图，蓝色曲线为本方法的角度波形图，峰值为15.03°，红色曲线为SIMO雷达系统的角度波形图，此时雷达不受多普勒偏移影响，无需进行运动补偿，目标角度为15.01°，目标实际角度为15°，角度误差分别为0.03°和0.01°。绿色曲线为基于多普勒频率相位的运动补偿方法的角度波形图，角度估计值为8.6°，与实际值15°相差6.4°，偏差较大，且波形图曲线与SIMO系统相比走势相差较大。造成巨大误差的原因是该方法利用目标检测获得目标速度，根据速度估计相位误差，从而进行补偿，补偿精度依赖于速度估计精度。仿真中目标3的速度为-20 m/s，超过了不模糊速度范围，速度估计出现巨大偏差，因此角度估计结果偏差较大。本方法与SIMO雷达系统角度误差较小，准确率较高，而且角度波形图走向大致相同。实验结果表明，对单目标进行运动补偿后，可以有效地解决多普勒-角度耦合问题，从而实现目标角度的精确估计。

为了验证多目标的有效性，对3个仿真目标进行运动补偿，目标角度估计的均方根误差定义为

其中，θ1i,θ2i,θ3i为角度估计值，α1i,α2i,α3i的角度实际值，Lc为蒙特卡罗实验次数，RMSE为角度估计值均方根误差。多目标结果图如图9所示。

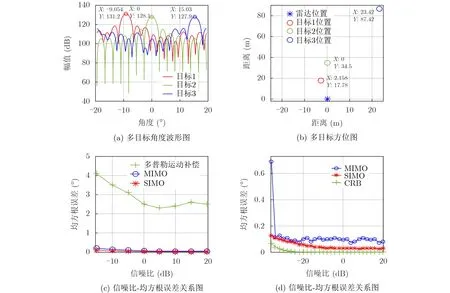
图9 多目标结果图

图9(a)中3个不同颜色的波形分别对应着3个不同目标的角度波形图，峰值对应的位置即为目标的方位角，目标1、目标2和目标3的角度分别为-9.05°,0°, 15.03°，目标的真实角度为-9°,0°,15°，误差分别为0.05°, 0°, 0.03°，角度估计精度较高，具体角度值如表3所示。图9(b)为测量目标相对于雷达的位置，测量结果与目标实际位置一致。图9(c)表明，SIMO体制雷达的角度均方根误差最终保持在0.03°。MIMO体制雷达的角度均方根误差最终保持在0.1°，相较于SIMO体制雷达，误差保持在0.07°，满足实际应用需求。而基于多普勒频率相位的运动补偿方法因为不适用于速度模糊的场景，因此角度误差较大。图9(d)给出了相应的克拉默-拉奥界[20](Cramer-Rao Bound, CRB)作为参考，随着信噪比的增大，其均方根误差逼近克拉默-拉奥下界。实验结果表明，在多目标场景下，运动补偿算法依然有效，能够实现多目标角度的精确估计。

图6-图9和表3仿真结果表明，多目标场景下，经过速度解模糊后可以有效地估计目标实际速度，而且在保持估计精度的同时增大了不模糊测速范围，速度误差为0.1 m/s，满足实际测速需求。经过运动补偿和迭代校正后，雷达可以有效地解决多普勒-角度耦合问题，而且运动补偿后的角度误差为0.1°。本方法可以有效地避免多目标匹配问题，保证了多目标估计的高效性。

3.2 实测验证

为了进一步验证本方法在实际雷达系统中的可行性，利用毫米波雷达在实测场景中采集车辆目标的回波数据，实测场景为城市道路双向车道，将雷达置于天桥上方，面对车道正向采集数据，检测目标为运动的车辆目标，雷达参数如表1所示，目标参数如表4所示，实测场景如图10所示。

表4 目标参数

图10 实测场景

分别选取运动目标数为2个和9个的场景进行实测验证。通过恒虚警检测，在2维频谱图中分辨出多个运动目标，对每个目标进行角度估计，从而实现多目标的距离、速度和角度估计。选取第1个接收天线的2维频谱图进行分析，2维频谱图如图11所示。

图11 2维频谱图

图11(a)和图11(b)表明，雷达检测到两个有效目标，并得到目标1和目标2的距离、模糊速度和相位信息，其中目标1的速度为3.15 m/s，目标2的速度为10.53 m/s，经过速度解模糊后目标1和目标2的速度分别在模糊数为1和0的速度区间内，所以目标1存在速度模糊，解模糊后的速度为16.93 m/s，而目标2不存在速度模糊，与实际速度17 m/s和10.5 m/s基本吻合，速度误差小于0.5 m/s，证明了速度估计的准确性。图11(c)和图11(d)表明，在多目标场景中，通过CFAR检测到9个有效的运动目标，分别对每个目标进行解角，最终实现了多目标场景下的参数估计。为了便于参数估计结果分析，选取2个目标的测试结果进行分析。

提取目标的最大峰值点云进行角度估计，对多目标角度波形图进行结果分析，目标结果图如图12所示。

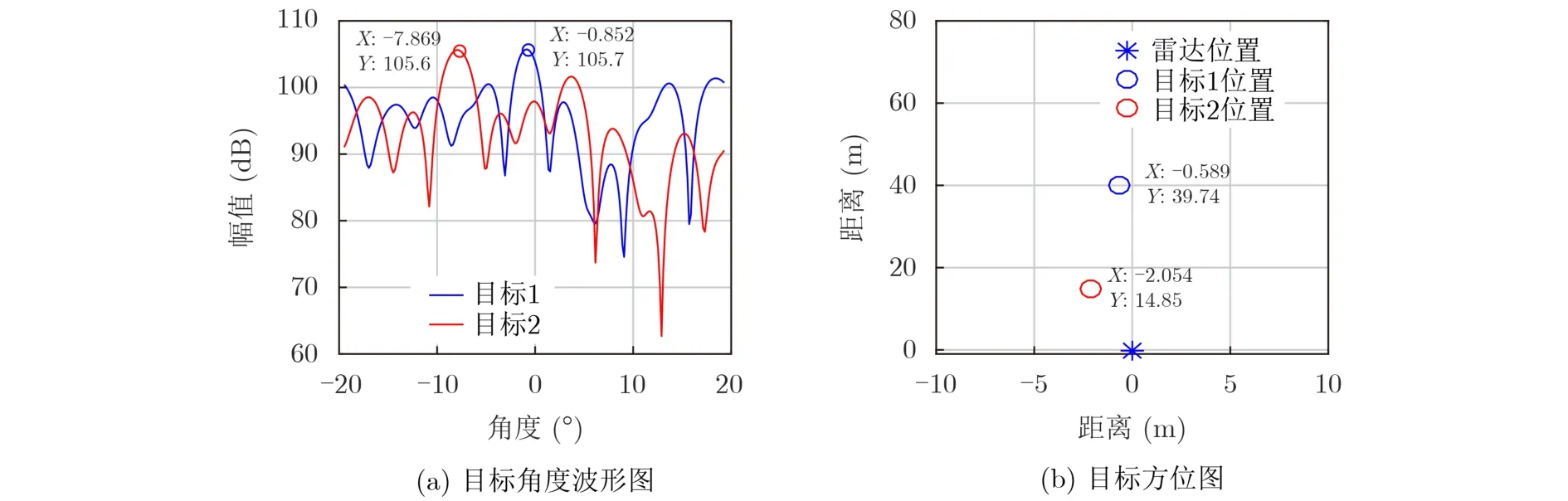
图12 多目标结果图

图12(a)中目标1和目标2的角度分别为-0.85°和-7.87°，与实际角度-1°和-8°基本吻合。图12(b)为目标相对于雷达的位置，测量位置与目标实际位置相吻合。

实测结果表明，在实际交通场景中，基于重叠阵元天线阵列的多目标参数估计算法具有较好的估计效果，满足实际交通应用需求，验证了雷达系统的可行性。

4 结束语

针对TDM-MIMO雷达探测运动目标时因速度-多普勒耦合和速度模糊导致角度和速度估计精度降低的问题，提出了基于重叠阵元的运动补偿和速度解模糊方法。在多目标场景下，通过仿真分析和实测验证，该方法能够有效地补偿多普勒频偏实现多普勒-角度的解耦合，并通过迭代校正阵元位置误差提高了角度估计精度。通过粗估计速度和模糊速度相结合的方法实现了速度解模糊，并通过频谱搬移的方式避免了解模糊过程中存在的速度跳变问题，在保持速度估计精度的同时扩大了雷达可探测速度范围。此外，本方法避免了多目标匹配并表现出优异的整体性能，可应用于任意MIMO雷达系统，适用于交通监测、自动驾驶、安防监控等领域。所提出的方法仍有优化空间，重叠阵元的应用导致孔径减小，影响了角度分辨率。因此，如何提高角度分辨率是本文进一步研究的方向。