基于时-频注意力机制网络的水声目标线谱增强

古天龙 张清智 李晶晶*

①(暨南大学可信人工智能教育部工程研究中心 广州 510632)

②(桂林电子科技大学广西可信软件重点实验室 桂林 541004)

1 引言

利用辐射噪声对目标进行检测是水声信号处理领域的重要内容[1,2]。水下目标的辐射噪声具有丰富的线谱成分，特别是在低频段，提取该线谱成分对水下低噪声安静型目标的检测具有十分重要的意义，因此LOFAR(Low Frequency Analysis Record)线谱检测是被动声纳目标检测的重要内容，然而，由于水声环境复杂，线谱信息淹没在噪声干扰中，难以提取。

随着深度学习技术在水声传感中的广泛应用[3-10]，一些研究者开始探索基于深度学习的线谱增强方法。Ju等人[11,12]从时域数据出发，利用自适应线谱增强器(Adaptive Line Enhancer, ALE)原理[13]，设计了基于深度学习的线谱增强器(Deep-learningbased Line Enhancer, DLE)，采用自编码神经网络代替传统滤波器，增强了系统在时域处理的非线性，提升了低信噪比下的LOFAR谱的线谱检测效果。杨路飞等人[14]直接针对LOFAR谱，提出双层长短时记忆网络(Long Short-Term Memory, LSTM)，利用LSTM处理时序数据的能力，将LOFAR谱中每个频率对应的值分别作为网络输入，增加了网络在频域处理的非线性，实现了对LOFAR谱的线谱增强，并提出通过高斯白噪声实验来验证模型线谱增强的合理性。LSTM由于同时具有时域和频域非线性处理能力，其比DLE具有更高的灵活性。然而，LSTM模型对输入信噪比有要求，在低输入信噪比的情况下线谱增强效果较差。

本文提出基于时-频注意力机制的线谱增强网络模型(Time-Frequency Attention Network,TFA-Net)，在LSTM的基础上同时增加了时域注意力机制模块和频域注意力机制模块，提升了基于LSTM的线谱增强效果。其中，时域注意力机制模块，使网络更关注对LSTM产生重要影响的时刻的数据。频域注意力机制模块采用了改进的深度残差收缩网络(Deep Residual Shrinkage Network,DRSN)，使频域注意力阈值可以更加精准地区分线谱和噪声。本文的技术路线图如图1所示。

图1 技术路线图

本文提出了LSTM和DRSN相结合的网络模型，实现了时域数据处理和频域数据处理的有效融合；运用了时-频注意力机制模块，提取了目标信号在时域与频域的双重重要特征；构建了残差卷积收缩模块，通过将收缩子网络中的全链接层设计为1维卷积层，获得更为合理的频域注意力阈值，从而更加精准地区分线谱和噪声；大量的实验结果表明，相比于LSTM，所提出的TFA-Net具有更高的系统信噪比增益：在输入信噪比为-3 dB的情况下，将系统信噪比增益由2.17 dB提升到12.56 dB；在输入信噪比为-11 dB的情况下，将系统信噪比增益由0.71 dB提升到10.6 dB。

2 DLE和基于LSTM的线谱增强模型

图2为DLE和基于LSTM的线谱增强模型的结构示意图。

图2 DLE和基于LSTM的线谱增强模型结构

DLE由自编码神经网络计算滤波输出，其输入节点个数为N，N为滤波器阶数，记第k时刻的时域信号为s(k)，输入节点的输入数据依次为s(k-Δ),s(k-Δ-1), ···,s(k-Δ-N+1)，Δ为延时步长，以s(k)作为标签，输出节点个数为N。DLE利用了深度神经网络(Deep Neural Networks, DNN)的非线性结构，提升系统增益[15,16]。

基于LSTM的线谱增强模型，以输入信号的LOFAR谱作为输入，通过LSTM网络计算滤波输出。记LOFAR谱中第k时刻的功率谱为xk ∈RM×1，M为LOFAR谱中的频率个数，每个频率对应一个输入节点，即输入节点个数为M。第m个输入节点的输入数据为一组时间序列数据xk-Δ(m,1),xk-Δ-1(m,1), ···,xk-Δ-N+1(m,1)，N为输入时间序列长度，由于长短时记忆网络的特性，N一般比N小得多。以xk为标签，输出节点个数为M。由于每个输入节点数据的维数为N×1，每个输出节点数据的维数为1×1，即属于序列到序列(Sequenceto-Sequence, Seq2Seq)中的多对一模式。

综上所述，由于LSTM具有对时序数据的记忆能力[17-19]，其在网络结构上可以以各频谱分量作为网络输入。一方面，网络可训练参数增多，另一方面对网络参数的训练，同时体现在时域和频域，因此，LSTM比DLE具有更高的灵活性。

3 基于时-频注意力机制的线谱增强网络

3.1 模型结构

基于时-频注意力机制的线谱增强网络，在LSTM的基础上同时增加了时域注意力机制模块和频域注意力机制模块。其中，时域注意力机制模块借助LSTM的隐藏状态，计算各时间序列的注意力分布，产生新的时间序列数据，使网络更关注对LSTM产生重要影响的时刻的数据。频域注意力机制模块采用了改进的深度残差收缩网络，其由多个堆叠的深度残差收缩模块组成，每个残差收缩模块在传统残差收缩模块的基础上，将收缩子网络中的全链接层设计为1维卷积层，使频域注意力阈值可以更加精准地区分线谱和噪声。基于时-频注意力机制的线谱增强网络的模型结构如图3所示。

图3 基于时-频注意力机制的线谱增强网络模型结构

TFA-Net的算法流程如下：

(1) 获取目标辐射噪声信号LOFAR谱[14]；

(2) 选取延时步长Δ、时序数据长度N；

(3) 将得到的时序数据按照时间序列排序，即x1=xk-Δ-N+1,x2=xk-Δ-N,...,xN=xk-Δ，将x1,x2,...,xN输入到LSTM层中，借助LSTM的隐藏状态h1,h2,...,hN，计算各时间序列的注意力分布，产生特征向量V=[v1,v2,...,vN]；

(4) 将特征向量输入频域注意力机制模块；

(5) 频域注意力机制模块的输出为xk-Δ经滤波后的值，目标函数公式

其中，P为样本数，网络模型迭代训练，模型收敛后输出训练后的LOFAR谱。

3.2 时域注意力机制模块

基于LSTM的LOFAR谱的线谱增强任务属于Seq2Seq的多对一模式，由于LSTM对时序数据具有记忆能力，传统LSTM只保留最后一个时刻隐藏状态作为输出。该文提出的时域注意力机制模块，同时考虑所有隐藏状态，加强模型对先前隐藏状态的记忆，并通过计算每个时刻隐藏状态与最后一个时刻隐藏状态的关联，获取每个时刻隐藏状态的记忆权值。

时域注意力机制模块的结构如图4所示，通过3个步骤实现。首先，由于LSTM最后一个时刻隐藏状态的可信度最高，以最后一个时刻的隐藏状态hN作为查询(query)，以每个时刻的隐藏状态hi作为键(key)，计算两者的相似性，得到第i个时刻的隐藏状态hi的注意力分值ei。该文选择的相似性计算函数为余弦相似度。

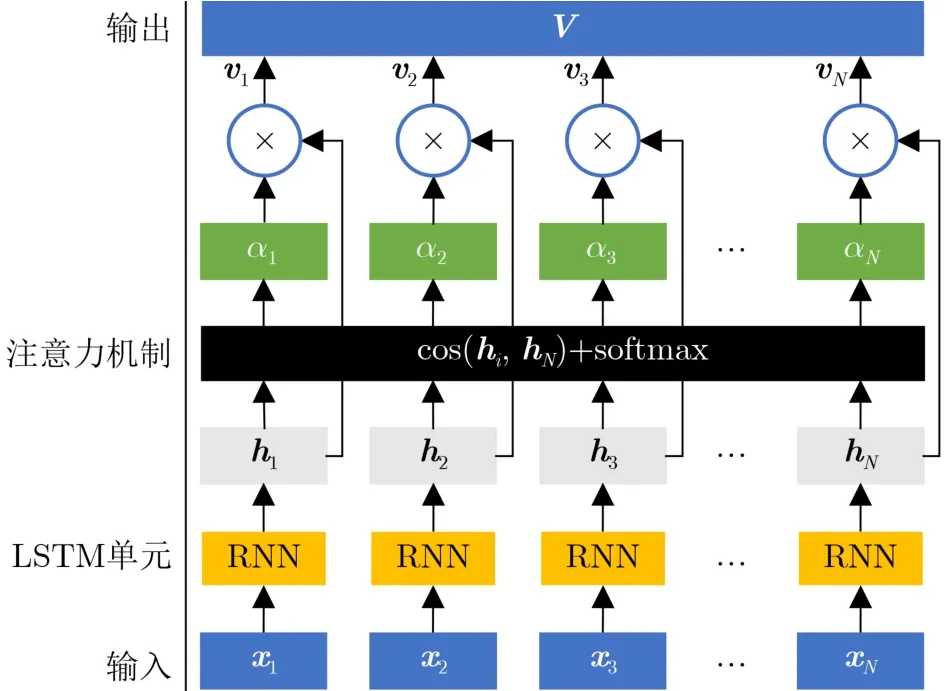
图4 时域注意力机制模块结构

其次，引入softmax函数对注意力分值进行数值转换，对原始注意力分值进行归一化处理，得到权重系数αi。αi表示第i个时刻隐藏状态的重要程度。

最后，以每个时刻的隐藏状态hi作为值(value)，根据权重系数对值进行加权，得到加权后的隐藏状态vi。

考虑到后续频域注意力机制模块的输入数据格式，时域注意力机制模块的输出设计为由vi组成的向量V=[v1,v2,...,vN]，维数为M×N×1。

3.3 频域注意力机制模块

频域注意力机制模块采用改进的深度残差收缩网络，使频域注意力阈值可以更加精准地区分线谱和噪声。其由改进的深度残差收缩模块堆叠而成，每个残差收缩模块在传统残差收缩模块的基础上，将收缩子网络中的全链接层设计为1维卷积层。改进的深度残差收缩模块命名为残差卷积收缩模块。

残差卷积收缩模块结构如图5所示。模块输入是时域注意力机制模块的输出V，将每个频率所对应的N×1的向量作为一个输入通道，输入的通道数为M。首先，输入V经过2次1维卷积，卷积后的特征向量记为B={b1,b2,...,bM}，卷积核大小D=1×1，卷积核的通道数为M，卷积核的个数K=M，步长S=1。然后，特征向量B直接作为收缩子网络的输入，在子网络中B经过2次1维卷积和sigmoid函数取值，得到缩放参数β，将β乘到相应的特征向量B中，得到针对各特征的自适应阈值τ。

图5 残差卷积收缩模块结构

其中，⊗表示按元素相乘。最后，将特征向量B和阈值τ按元素软阈值化，再和模块输入V按元素相加，得到频率注意力机制模块的输出。

其中，⊕表示按元素相加，ητ(B)表示软阈值函数，用于将绝对值低于某一预设阈值的输入数据设置为零，同时使得绝对值大于该阈值的输入数据朝着零收缩。

4 实验结果

为了验证该文所提出的TFA-Net的有效性，本节分别用仿真数据和实测数据进行实验。实验在Python(版本：3.7)平台Pytorch(版本：1.10)深度学习库上进行。所构建模型的超参数设置如表1所示。训练样本个数P由LOFAR谱的时间长度NS、选定的延时步长Δ、时序数据长度N决定，P=NS-N-Δ+1。

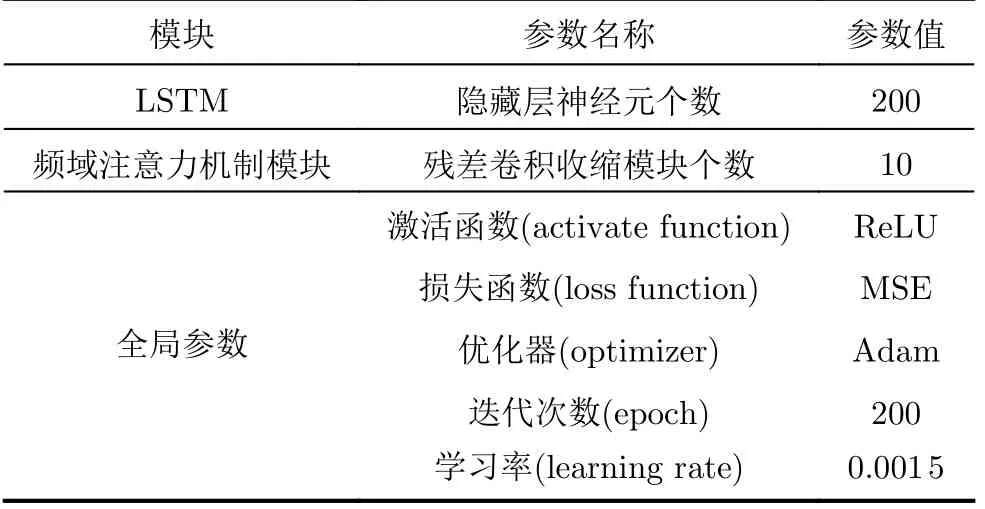
表1 TFA-Net模型超参数设置

4.1 仿真实验验证

仿真实验分为高斯白噪声实验和目标线谱实验。其中高斯白噪声实验的目的是验证模型的抗虚警能力[14]，当高斯白噪声训练后的图谱没有出现连续的线谱，则可证明模型线谱增强效果的可靠性。目标线谱实验的目的是验证网络模型在低信噪比下的线谱增强效果，仿真实验信号由公式

产生，其中，Q表示线谱个数，k表示采样时刻，Ai,fi和φi分别表示第i个线谱的幅值、频率和初始相位，n(k)为高斯白噪声。对仿真信号幅值进行归一化后，采用短时傅里叶变换(Short-Time Fourier Transform, STFT)求取LOFAR谱。LOFAR谱的时域长度NS由信号时长TP、采样频率fS、窗口长度NW和重叠率σ计算

4.1.1 高斯白噪声实验

高斯白噪声实验的参数如下：TP=6.553 6 s,fS=25 kHz,NW=1 024,σ=0.5，频率间隔为20，最大显示频率为4 000 Hz。选择延时步长Δ=1，序列长度N=3，由计算可得，样本数P=316，频率个数M=201。

实验结果如图6所示，其中图6(a)为训练前高斯白噪声LOFAR谱，图6(b)为LSTM训练后高斯白噪声LOFAR谱，图6(c)为TFA-Net训练后高斯白噪声LOFAR谱。由图中可以看出，经TFA-Net和LSTM训练后的LOFAR谱均未出现线谱，证明了TFA-Net具有较高的抗虚警能力。

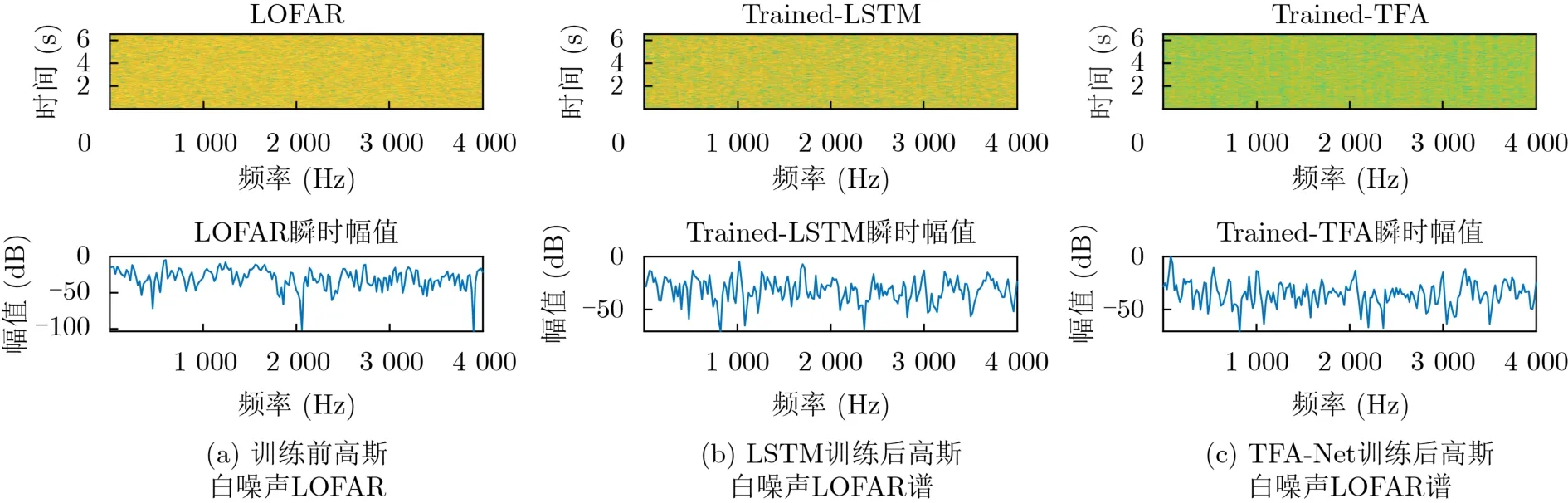
图6 高斯白噪声实验结果

4.1.2 目标线谱实验

目标线谱实验包含3部分内容：线谱增强实验、消融实验和网络深度寻优实验。其中线谱增强实验对比了不同输入信噪比下，所提出的TFA-Net与传统基于LSTM的线谱增强网络的线谱增强效果；消融实验展示了移除时间注意力模块和频率注意力模块后，模型的线谱增强效果；网络深度寻优实验探讨了深度残差卷积收缩网络中残差块的堆叠层数对模型线谱增强效果的影响。

(1) 线谱增强实验

目标辐射噪声仿真信号由4个频率组成，即Q=4，其频率和幅值分别为f1=100 Hz,A1=4.5,f2=220 Hz,A2=2.5,f3=365 Hz,A3=4,f4=1500 Hz,A4=6，噪声为高斯白噪声，TP=19.660 8 s,fS=25 kHz,NW=1024,σ=0.5，频率间隔为20，最大显示频率为4 000 Hz。选择延时步长Δ=1，序列长度N=3，由计算可得，样本数P=959，频率个数M=201。

图7为输入信噪比为-3 dB时的实验结果，其中，图7(a)为训练前目标信号LOFAR谱，图7(b)为LSTM训练后目标信号LOFAR谱，图7(c)为TFA-Net训练后目标信号LOFAR谱。为了量化所提出模型及对比模型线谱增强的效果，定义系统信噪比增益[20,21]

图7 输入信噪比为-3 dB时的线谱增强结果

其中，SNRin和SNRout分别表示训练前和训练后的LOFAR谱的图像信噪比，以训练前的LOFAR谱的图像信噪比为例，计算公式为

其中，Nx,Ny分别表示LOFAR谱矩阵的行数和列数，fˆin(x,y)表示训练前含噪声的LOFAR谱中像素点(x,y)处的像素值，f(x,y)表示不含噪声的LOFAR谱中像素点(x,y)处的像素值。为方便对比，在计算LOFAR谱信噪比时，将含噪声的LOFAR谱和不含噪声的LOFAR谱的取值范围统一，且以最小值作为0 dB。表2所示为系统信噪比增益对比。

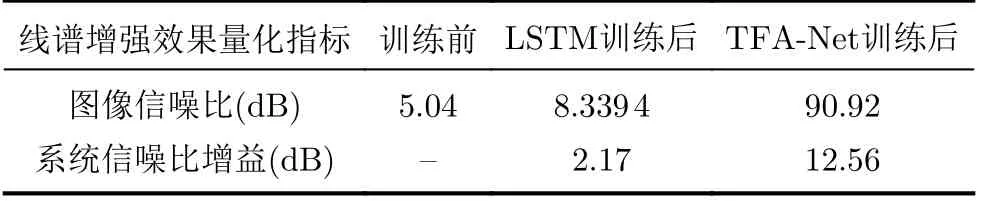
表2 输入信噪比为-3 dB时的系统信噪比增益对比

由图7可以看出，训练前的LOFAR谱中4条线谱淹没在噪声干扰中，尤其是220 Hz处的线谱，由于幅值较小，难以被观察到。经LSTM训练后，LOFAR谱中4条线谱均得到增强，可以观察到220 Hz处的线谱，但系统的信噪比增益仅为2.17 dB。经TFANet训练后，4条线谱得到明显增强，220 Hz处的线谱清晰可见，系统的信噪比增益为12.56 dB。

为进一步验证所提出的基于时-频注意力机制的线谱增强网络的有效性，对不同输入信噪比下LSTM和TFA-Net两个网络模型的系统信噪比增益进行对比，图8所示为不同输入信噪比下的系统信噪比增益对比曲线。由图中可以看出，相比于LSTM，所提出的TFA-Net具有更高的系统信噪比增益，且在输入信噪比为-11 dB的情况下，仍然能得到10.60 dB的系统信噪比增益。

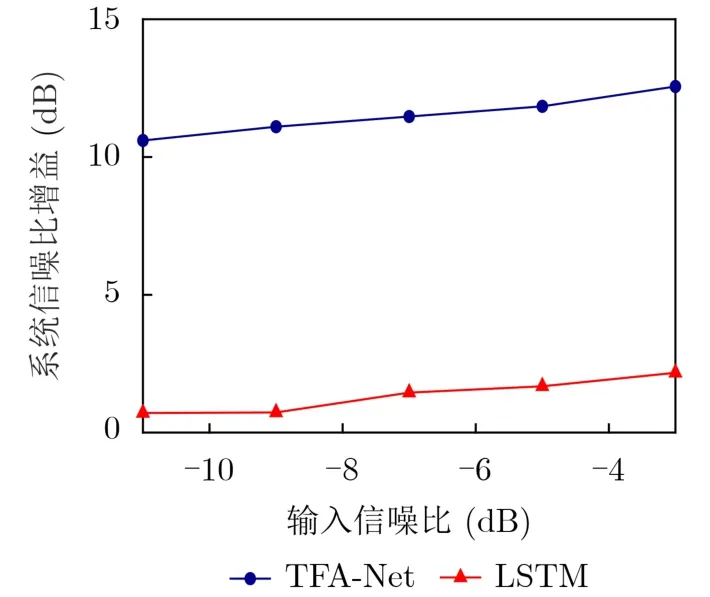
图8 不同输入信噪比下系统信噪比增益对比曲线

(2) 消融实验

为了验证所提出的TFA-Net中时域注意力机制和频域注意力机制的有效性，分别移除TFA-Net中的3个重要模块，即时域注意力机制模块、深度残差收缩模块、卷积改进模块，对比移除后模型的线谱增强结果。实验结果如表3所示。其中，由于卷积改进模块是针对深度残差收缩模块的改进，移除深度残差收缩模块后将无法进行卷积改进，因此，不存在只移除深度残差收缩模块的情况，表3仅给出了5组对比实验。另外，由于深度残差收缩模块和卷积改进模块共同构成频域注意力机制模块，所以将同时移除深度残差收缩模块和卷积改进模块，用移除频域注意力机制模块表示。

表3 消融实验结果

由表中可以看出，移除任意模块后，系统的信噪比增益都有所下降。其中同时移除时域注意力机制模块和频域注意力机制模块后效果最差，其次是同时移除时域注意力机制模块和卷积改进后效果下降明显，证明了时间注意力机制和频率注意力机制相结合的有效性。

(3) 网络深度寻优实验

为了探索残差卷积收缩网络深度对线谱增强效果的影响，构建不同网络深度的TFA-Net进行训练，实验结果如图9所示，其中图9(a)、图9(b)、图9(c)分别表示堆叠6个、10个和18个残差模块时的线谱增强效果。

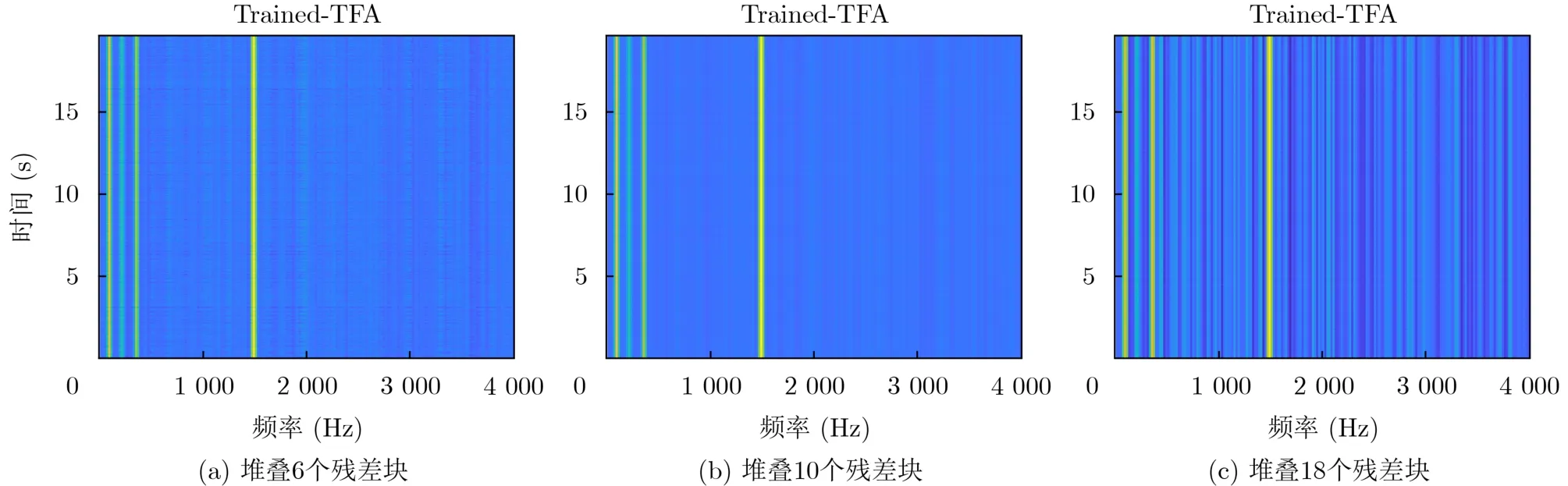
图9 不同网络深度下的线谱增强效果对比

由图中可以看出，当网络深度较浅时，增强后的LOFAR谱在时间上出现较强干扰，即如图9(a)所示，所有频率处的能量在时间上有强烈波动，目标线谱出现时间上的断续。当网络深度较深时，LOFAR谱在频率上出现强干扰，在多个非目标频率处出现能量较高的虚假线谱，最强的虚假线谱能量为5.12 dB。当网络深度选择适当时，增强后的LOFAR谱在时间和频率上均有令人满意的表现，如图9(b)所示。网络深度实验的结果可用来指导网络深度的选择，对TFA-Net在线谱增强的应用具有重要意义。

4.2 实测数据实验

实测数据是在中国某海域里利用水听器收集到的信号，TP=6.5536 s,fS=25 kHz,NW=1 024,σ=0.5，频率间隔为20，最大显示频率为4 000 Hz。选择延时步长Δ=1，序列长度N=3，由计算可得，样本数P=316，频率个数M=201。图10所示为实验结果，其中，图10(a)为训练前实测数据LOFAR谱，图10(b)为LSTM训练后实测数据LOFAR谱，图10(c)为TFA-Net训练后实测数据LOFAR谱。

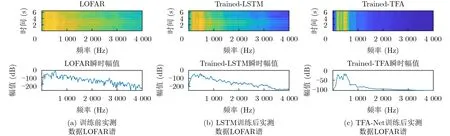
图10 实测数据实验结果

由图中可以看出，相比于LSTM, TFA-Net的线谱增强效果明显，可以清楚观察到200 Hz,440 Hz, 520 Hz等几个低频段的线谱，证明了TFANet在处理复杂背景噪声数据的有效性。

5 结束语

该文针对基于LSTM的LOFAR谱的线谱增强效果不理想的问题，提出基于时-频注意力机制的线谱增强网络模型，利用LSTM隐藏状态之间的关联性，增加模型在时域的注意力，通过在深度残差收缩网络中提取频域特征，增加模型在频域的注意力，克服了LSTM同时处理时域和频域特征时的兼顾问题，实现了系统信噪比增益的大幅提升。大量基于仿真数据和实测数据的实验表明，TFA-Net可以有效提升LOFAR谱的线谱增强效果，解决水下低噪声安静型目标的检测问题。此外，网络深度实验的结果也为TFA-Net的具体应用提供了经验指导。