基于图分级的水下有向传感器网络栅栏覆盖策略

常 娟 申晓红 王海燕 赵红言 李祥祥

①(西北工业大学航海学院 西安 710072)

②(空军工程大学基础部 西安 710051)

1 引言

近年来，随着我国海洋事业的发展，对水下移动目标，特别是对离陆地较近的浅海海域内移动目标的入侵检测已经成为我国水声传感器网络技术发展的重点之一。决定检测水平的基本要素就是网络覆盖的质量，水下传感器网络的覆盖问题已经开始得到广泛关注[1-5]。在不同的应用场景中，需要有不同类型的覆盖，环境感知和监测网络的覆盖主要分为3种：用于监测目标点的目标覆盖，用于监测所有监测区域的面覆盖和用于入侵检测的栅栏覆盖[6,7]。目前，很多有关水下入侵检测的栅栏覆盖的研究都是基于各向同性的传感器进行的，这种传感器的感知区域通常被建模为圆盘模型。只要入侵目标在感知区域内就会被检测到。但在入侵检测中，用于探测的传感器往往是有向感知的。与全向传感器不同，有向传感器的感知范围不仅取决于传感器的感知半径，还取决于它的感知方向角和偏移角，因此有向传感器网络的栅栏覆盖问题复杂度更高。

关于有向传感器网络栅栏覆盖问题，大量成果利用尽可能少的移动节点进行方向角旋转，旋转角度尽可能小来对栅栏进行增强。文献[8]通过一个新的全视角覆盖模型，将部署区域划分为若干连接的网格并提出了基于网格的部署策略为每个网格部署传感器。文献[9]利用了虚拟力和虚拟边界转距的概念提出了栅栏增强部署算法解决了可移动、旋转的异构传感器网络的栅栏增强问题。文献[10]首次提出了可行方向范围的概念，并提出一种在可行性范围内选择传感器方向的快速算法，通过调整节点的方向角来填补栅栏空洞。文献[11]将有向传感器网络目标栅栏覆盖问题转化为更简单的优化问题，采用一种分布式粒子群算法利用调节节点的方向角来填补空洞，对栅栏进行优化。文献[12]提出了一种新的基于网络区域的聚类算法来减少信息交换，再提出了一种启发式算法利用最小移动距离来弥补漏洞修复栅栏。也有学者直接根据有向传感器节点的最小旋转角度来构建栅栏。文献[13]研究异构视频传感器网络全视角覆盖估计问题，为消除边界效应，提出了扩展监测区域及最大探测区域的概论，并推导出目标全视角覆盖估计模型，采用该模型减小了平均绝对覆盖误差。文献[14]首次定义了安全单元并设计了查找安全单元和栅栏空隙的算法，提高了栅栏覆盖率。以上算法仅讨论了如何利用移动传感器来构建栅栏或对栅栏漏洞进行弥补，未深入讨论如何对静态传感器网络进行首次栅栏覆盖问题。由于水下传感器网络能量十分有限，在水下传感器网络栅栏覆盖中，通常希望在首次栅栏构建中就能够只采用静态节点成功构建栅栏，以减少二次栅栏构建带来的传感器资源浪费。

文献[15]提出了一种分布式扩散算法，在有向传感器网络栅栏的首次构建阶段采用了Dijkstra算法对局部网络的静态节点进行搜索选择，再利用移动节点进行补充来构成完整的栅栏。该算法解决了采用尽可能少的移动节点实现可旋转摄像机传感器的全视图栅栏覆盖问题。该算法中进行局部栅栏首次构建所采用Dijkstra算法，时间复杂度较高，构建栅栏所需的节点数也较多。但是为节约水声传感器资源，通常采用尽可能少的静态有向传感器构建栅栏。显然该算法并不适用于水下传感器网络的首次栅栏覆盖。

文献[16]首次在网络覆盖中提出了分级图的概念，通过对构建的覆盖图进行分级使传感器节点之间的拓扑关系更加清晰，在此基础上构建的栅栏所用的节点数较少。该算法研究了采用尽可能少的节点进行栅栏的首次构建问题，但主要针对静态全向水声传感器网络进行首次栅栏覆盖，不适用于静态有向水声传感器网络。全向传感器网络构建覆盖图时传感器之间的位置关系简单，只需根据传感器之间的距离和感知半径的关系来判断两个有向传感器的感知区域是否相交，进而构建网络覆盖图。而有向传感器之间位置关系判断比较复杂，要综合考虑传感器之间的距离和感知半径的关系，传感器方向角之间的关系和偏移角的大小。文献[17]从这两方面讨论了强栅栏覆盖的条件，并基于邻接矩阵给出了强栅栏覆盖算法，但分析不够全面，且该覆盖算法所需的节点数较多，且要求数据存储量较大。

在水声传感器网络覆盖中，通常认为海域深度小于传感器节点感知半径2 倍的海域为浅海海域，此时用于浅海入侵目标检测所用的水声传感器节点为2维分布。本文主要研究应用于浅海入侵目标检测的2维水下有向传感器网络的首次栅栏覆盖问题。本文首先研究有向传感器多种位置下建立连接关系的条件以便于建立有向传感器网络覆盖图，并在图分级的基础上研究了静态节点随机部署前提下，采用尽可能少的节点实现首次栅栏构建，以节约水下传感器资源。

2 传感器感知模型

有向传感器的感知范围为一个扇形区域，可表示为：〈s(x,y),Rs,α,β〉[3]，如图1所示，其中s(x,y)为传感器s的位置坐标，Rs为感知半径，α(0≤α ≤2π)为X轴正方向与扇形感知区域中心线的夹角，即方向角，β(0≤β ＜π)为扇形感知区域两侧的边界相对于其中心线的偏移角。当β= π时，感知模型为0/1布尔圆盘模型，因此0/1布尔圆盘模型是有向感知模型的特殊情况。

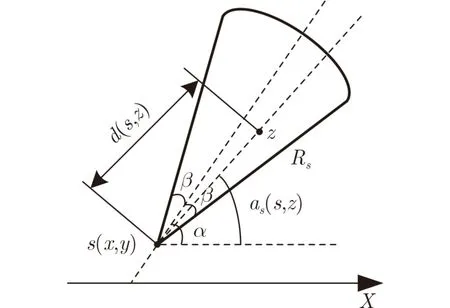
图1 有向感知模型

图1所示有向感知模型的数学表达式为

其中，d(s,z)为空间某一点z与传感器节点s之间的欧氏距离，as(s,z)为它们之间的夹角。

3 问题描述

本文主要研究以采用尽可能少的节点为目标，构建水下有向传感器网络栅栏的问题，为便于下文讨论，对研究的前提条件做一下假设：

(1)水声传感器网络由N个静止的有向传感器s1,s2,...,sN被随机分布在一个2维矩形区域A2-dim=[0, L] × [0, W]，其中L和W分别表示该矩形区域的长和宽，且各传感器是独立同分布的，如图2所示。

图2 随机分布下的有向传感器网络

(2)有向传感器网络中的每一个有向传感器都能够获取自己的位置信息，并能够通过一些定位算法得到与其他传感器之间的相对位置；

(3)有向传感器网络内所有节点都是静态的且同性质的，它们的感知半径、位置坐标和偏移角都相等且保持不变；

(4)有向传感器网络始终保持连通性。

4 基于图分级的有向传感器网络栅栏覆盖策略

基于图分级的有向传感器栅栏覆盖策略是基于覆盖图展开的[16]，在构建覆盖图的过程中需要各节点确定自己的感知区域与其每一个相邻节点的感知区域是否相交，即判断两节点在覆盖图中是否连接。能否正确判断两个节点之间的连接关系是构建覆盖图和栅栏的关键。

4.1 两个节点之间的连接判断方法

栅栏覆盖分为弱栅栏覆盖和强栅栏覆盖两种，定义如下：

定义1通过传感器网络覆盖，使沿任意垂直于带状区域的路径穿越带状区域的移动目标都能被传感器网络检测到的覆盖称为弱栅栏覆盖。在水声传感器网络中，弱栅栏覆盖主要针对机动性较弱的水下目标入侵进行检测。

定义2通过传感器网络覆盖，使沿任意路径穿越带状区域的移动目标都能被传感器网络检测到的覆盖称为强栅栏覆盖。在水声传感器网络中，强栅栏覆盖主要针对机动性较强的水下目标入侵进行检测。

与全向传感器不同，有向传感器的感知区域不仅受感知半径的限制，还受其水平角和偏移角影响。因此两个有向传感器之间连接关系的判断比较复杂。两个传感器感知区域相交的情况分为两种：弱连接和强连接。如果一条栅栏中两个相邻节点满足弱连接，则该栅栏是弱栅栏；如果一条栅栏中每两个相邻节点都满足强连接，则该栅栏是强栅栏。

定义3如果两个相邻节点感知区域的水平投影相交，则两个节点是弱连接。

定义4如果两个相邻节点感知区域相交，则两个节点是强连接。

4.1.1 弱连接

弱栅栏覆盖能够检测到沿垂直路径穿越监测区域的入侵者。将监测区域的下边界作为2维坐标系的水平坐标，监测区域的左边界作为2维坐标系的垂直坐标。当dx(s1,s2)≤2Rs时，这两个节点感知区域的水平投影才有可能相交。

当0≤β ≤π/2且dx(s1,s2)≤2Rs时，两个弱连接的节点有两种位置关系：

(1)两节点中的任一个节点不在另一个节点的水平投影中，这时又有4种位置关系。

(a)0＜α1-β ＜π/2 且π/2＜α2+β ＜π且Rscos(α1-β)+Rscos[π-(α2+β)]≥dx(s1,s2)时，位置关系如图3(a)所示；

图3 当0 ≤β ≤π/2时，两个弱连接的节点中的任一个节点不在另一个节点的水平投影中时的位置关系

(b)-π/2＜α1-β ＜0 且π＜α2+β ＜3π/2且Rscos[2π-(α1+β)]+Rscos[(α2-β)-π]≥dx(s1,s2)时，位置关系如图3(b)所示；

( c )0＜α1-β ＜π/2且π＜α2+β ＜3π/2且Rscos(α1-β)+Rscos[(α2-β)-π]≥dx(s1,s2)时，位置关系如图3(c)所示；

(d)-π/2＜α1-β ＜0 且π/2＜α2+β ＜π且Rscos[2π-(α1+β)]+Rscos[π-(α2+β)]≥dx(s1,s2)时，位置关系如图3(d)所示。

(2) 两节点中有一个节点在另一个节点的水平投影内。

(a)-π/2＜α1-β ＜π/2且dx(s1,s2)≤Rs时，位置关系如图4(a)所示；

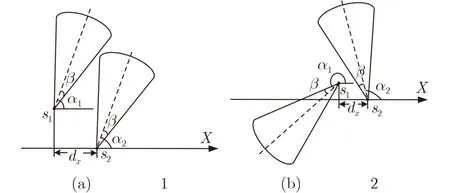
图4 当0 ≤β ≤π/2时，两个弱连接的节点中有一个节点在另一个节点的水平投影内时的位置关系

(b)π/2＜α2+β ＜3π/2且dx(s1,s2)≤Rs时，位置关系如图4(b)所示；

当π/2≤β ≤π且dx(s1,s2)≤2Rs时，两个弱连接的节点有两种位置关系：

(1)两节点中的任一个节点不在另一个节点的水平投影中，这时有3种位置关系。

(a)max{Rscos(2π-α1-β),Rscos(α1-β)}+max{Rscos(π-α2-β),Rscos(α2-β-π)}≥dx(s1,s2)且β ＜α1＜2π-β且2π-β ＜α2＜2π+β时，位置关系如图5(a)所示；

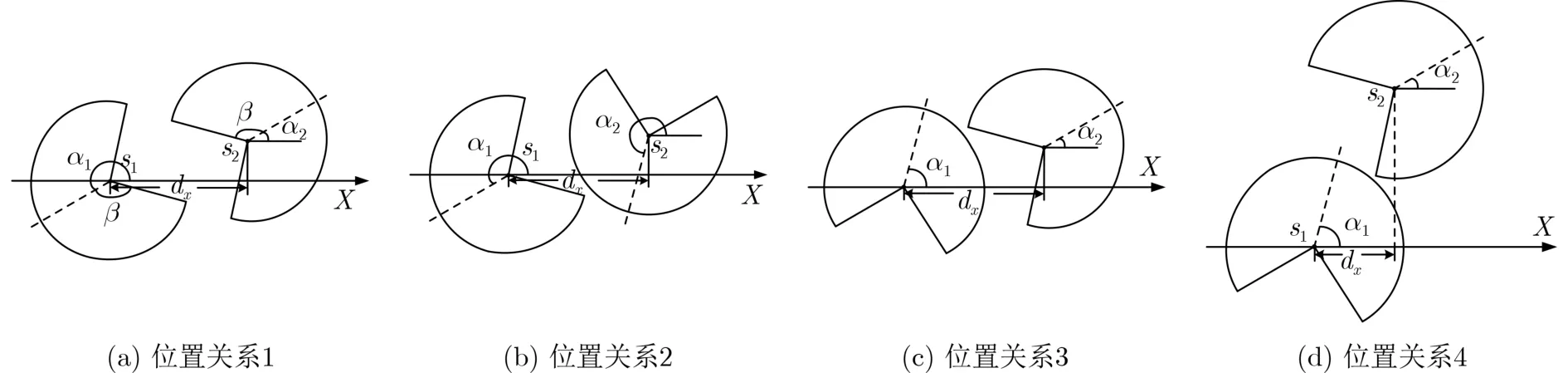
图5 当π/2 ≤β ≤π时，两个弱连接节点的位置关系

(b)Rs+max{Rscos(π-α2-β),Rscos(α2-β-π)}≥dx(s1,s2)且β ＜α1＜2π-β且0＜α2＜π/2 或3π/2＜α2＜2π时，位置关系如图5(b)所示；

(c)Rs+max{Rscos(2π-α1-β),Rscos(α1-β)}≥dx(s1,s2) 且π/2＜α1＜3π/2 且2π-β ＜α2＜2π+β时，位置关系如图5(c)所示；

(2)两节点中有一个节点在另一个节点的水平投影内时，dx(s1,s2)≤Rs，位置关系如图5(d)所示。

4.1.2 强连接

强栅栏覆盖能够检测到沿任意路径穿越监测区域的入侵者。水下有向传感器网络中，两个相邻传感器之间的位置关系判断更为复杂。为便于分析判断，每次将两相邻传感器的连线作为新的水平轴如图6所示。

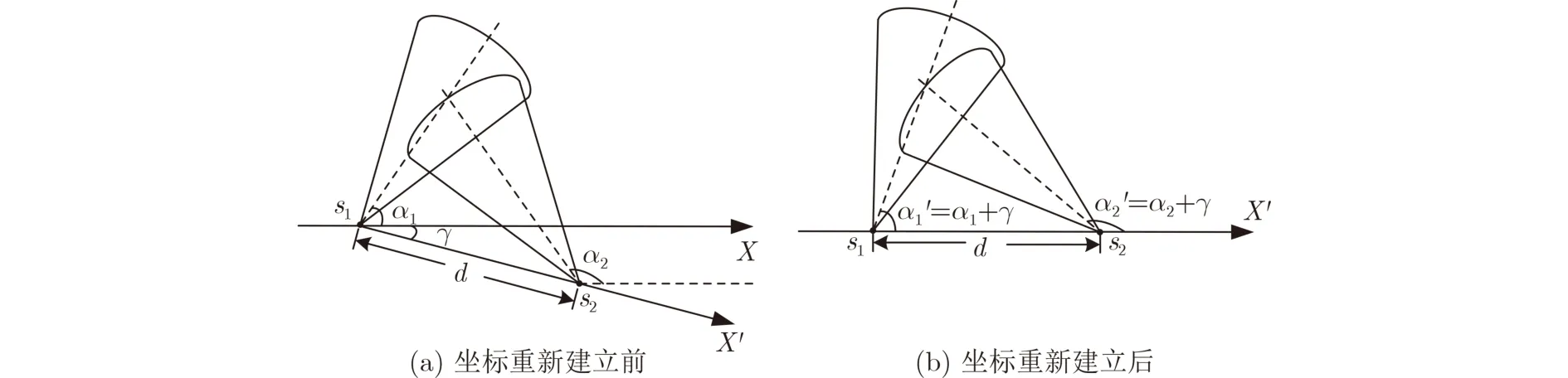
图6 水平坐标重新建立过程示意图

文献[1 7]给出了d(s1,s2)≤2Rs时，0≤β≤π/2 和π/2≤β ≤π两种情况下，两个强连接节点的位置关系。

4.2 基于图分级的有向传感器网络分布式强栅栏覆盖算法(Distributed strong barrier coverage algorithm in underwater Directional sensor network based on Hierarchy Graph, DDHG)

基于图分级的栅栏覆盖策略是在对网络覆盖图进行分级的基础上进行栅栏构建。经过分级的覆盖图可以更加清晰地反映网络的拓扑关系，在构建栅栏时每一个节点只需要知道自己相邻节点的位置和层级信息即可[16]。因此，基于图分级的栅栏覆盖策略既可用于集中式栅栏覆盖又可用于分布式栅栏覆盖。这里以分布式栅栏覆盖为例，讨论了一种基于图分级的分布式有向传感器网络强栅栏覆盖算法。

4.1节分析了两个有向传感器节点各种位置关系下分别满足弱连接和强连接的条件。依据这些条件各节点建立连接关系并构建覆盖图。对图2所示的有向传感器网络构建强栅栏覆盖图如图7所示，在此基础上建立的分级图如图8所示。在构建栅栏时，只要寻找与前一级和后一级某个节点都建立连接的节点即可，最后构建出的栅栏如图9所示。基于图分级的有向传感器网络弱栅栏覆盖算法中除了弱连接条件与基于图分级的有向传感器网络强栅栏覆盖算法中的强连接不同之外，后续的栅栏图和分级图的构建都相同。因此本文只给出基于图分级的有向传感器网络强栅栏覆盖算法(如算法1所示)。

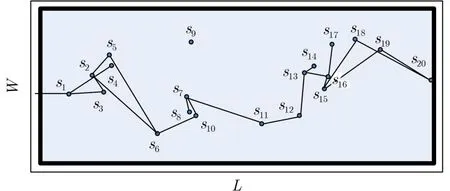
图7 有向传感器网络强栅栏覆盖图

图8 有向传感器网络分级图

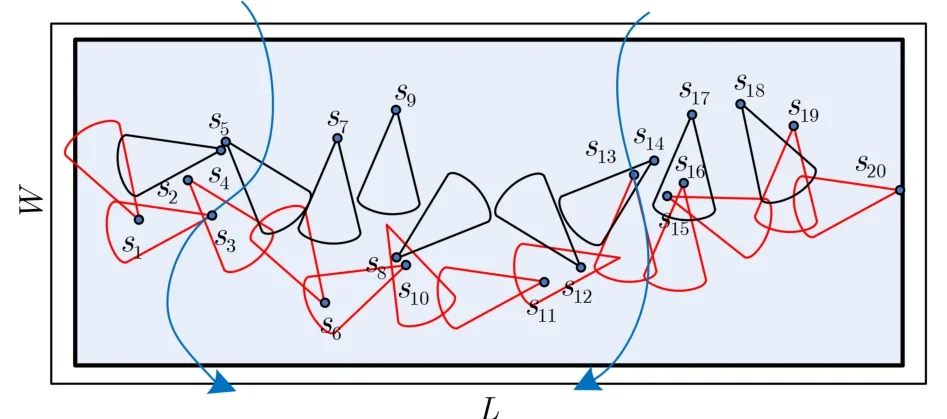
图9 随机分布下的有向传感器网络构建的强栅栏

5 性能分析

为了检验提出的DDHG算法性能，本文将从构建成功率、构建栅栏所需节点数和耗能3方面与文献[14, 15]中的分布扩散算法(Distributed Proliferation Algorithm, DPA)进行比较并进行讨论。水声传感器的偏移角通常在30°～120°，感知半径一般在500～1 000 m。为了研究有向传感器偏移角和感知半径对水声传感器网络栅栏覆盖的影响，仿真中通常取偏移角为30°, 60°和120°，感知半径在500～1 000 m进行比较讨论。仿真采用N个静态传感器构成的随机同分布的有向传感器网络，监测区域为10 000 m×500 m。为保证算法性能检验的可靠性，生成500个随机拓扑，并采用500次仿真结果的平均值。

5.1 栅栏构建成功率比较

图10比较了偏移角为β=60°，DDHG算法和DPA算法分别在感知半径为400, 500和600 m时构建1-强栅栏的成功率。构建成功率随着感知半径的增大而增大，并且采用DDHG算法的构建成功率稍低于采用DPA算法的构建成功率，特别在随机部署的节点数较多时，两种算法的差别不大。由该图可知：偏移角为β=60°，若构建半径为400 m，要使构建成功率达到85%以上，在该检测区域的随机部署节点数需达到400以上；若构建半径为600 m，要使构建成功率达到85%以上，随机部署节点数需达到300即可。

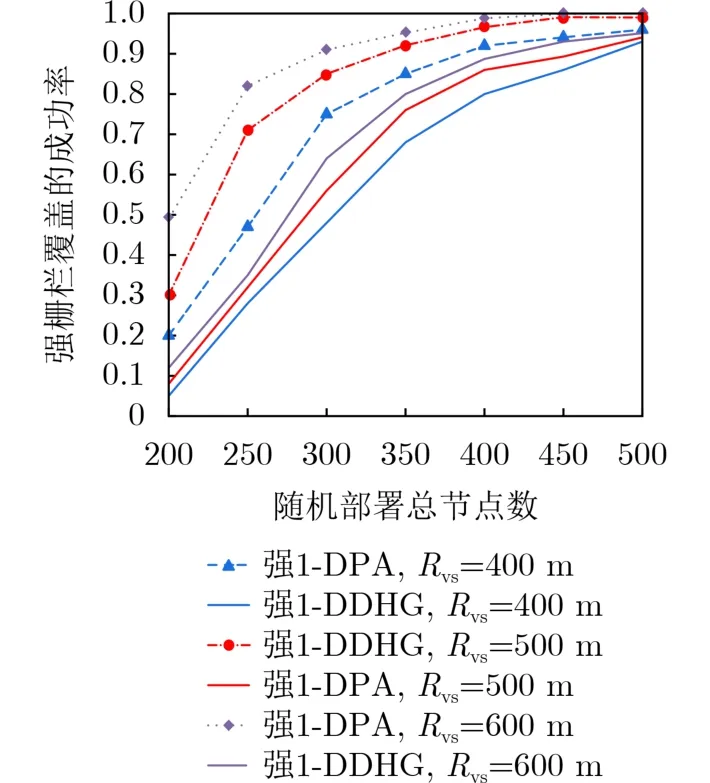
图10 不同构建半径下，采用两种算法构建1-强栅栏的成功率

5.2 节点个数和栅栏个数比较

图11比较了随机分布300个节点，采用两种算法在不同构建半径和不同偏移角下构建1-强栅栏所需的传感器数目。该图显示：构建1-强栅栏所需的传感器数目随着构建半径和偏移角的增大而减少，采用DDHG算法的构建栅栏所需的传感器数目小于DPA算法。

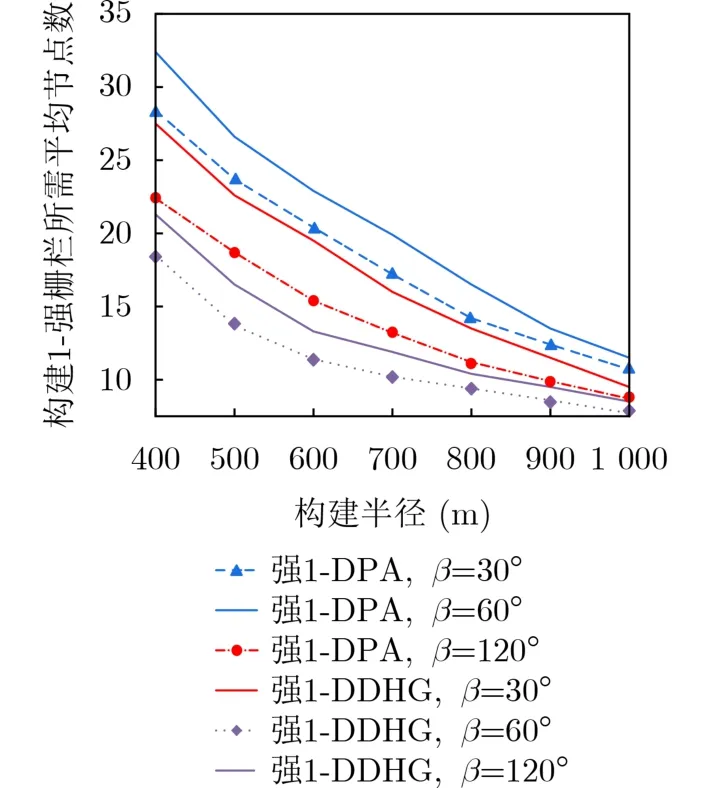
图11 不同构建半径下，构建1-强栅栏所需的传感器数目

图12比较了随机分布300个节点，采用两种算法在不同构建半径和不同偏移角下能够构建强栅栏的数目。构建的强栅栏数目随着构建半径和偏移角的增大而增多。采用DDHG算法能够构建的栅栏数比采用DPA算法构建的栅栏数多。

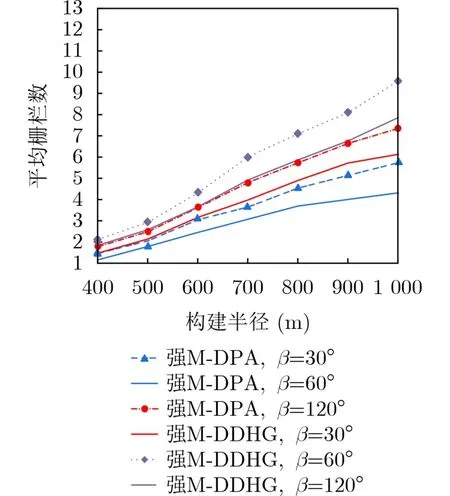
图12 不同构建半径下，构建强栅栏的数目

5.3 水声传感器网络检测概率比较

本小节比较了采用强M-DDHG算法和强M-DPA算法时水声传感器网络的检测概率。构建出多个栅栏的工作模式为多栅栏共同工作模式。

算法1 基于图分级的有向传感器网络强栅栏覆盖算法

图13比较了虚警概率Pf=0.1，随机部署总节点数为300，构建半径Rvs=700 m时，不同发射声源级和偏移角情况下，采用两种算法的网络检测概率。由该图可以看到：采用两种算法时网络的检测概率随着发射声源级和偏移角的增大而增大。多个栅栏采用共同工作模式下，采用强M-DDHG算法时网络的检测概率高于采用强M-DPA算法时网络的检测概率。并且当构建半径Rvs=700 m，发射声源级大于150 dB，偏移角大于60°时，采用强MDDHG 算法网络的检测概率可达到95%。

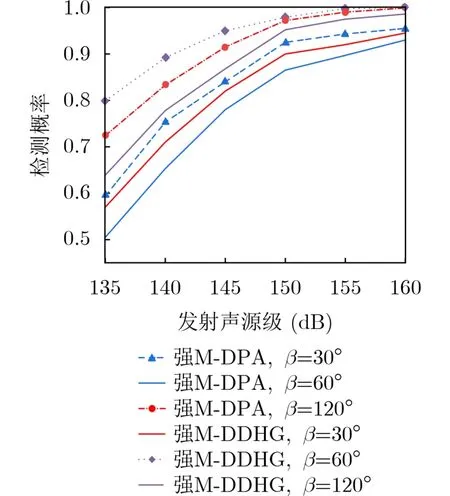
图13 不同发射声源级下，水声传感器网络的检测概率

5.4 水声传感器网络寿命比较

图14比较了随机部署总节点数为 300，构建半径和偏移角β不同时，分别采用两种算法时的网络寿命。这里构建出的多个栅栏采用交替工作模式来延长网络寿命。假设每一个传感器的寿命为2周。由该图可以看到：采用两种算法的网络寿命随着构建半径和偏移角的增大而增大，其中相同条件下采用强M-DDHG算法的网络寿命比采用强M-DPA算法的网络寿命长。原因有两个：一是如图13所示，采用强M-DDHG算法构建的平均栅栏数比采用强M-DPA算法的平均栅栏数多，参与交替工作的栅栏数也就更多；二是采用强M-DPA算法节点在构建栅栏过程中需要旋转方向角消耗能量，这也会导致网络寿命缩短。

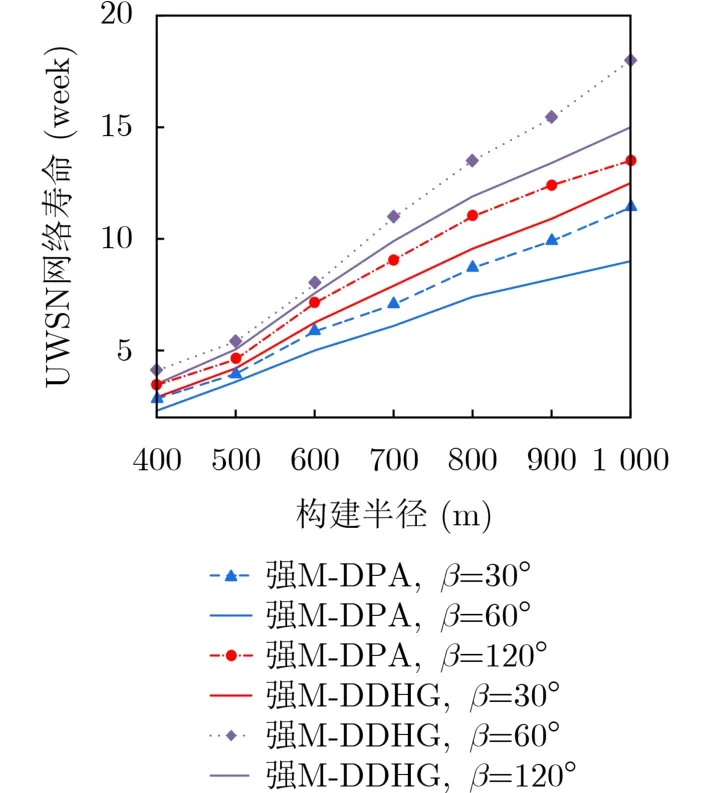
图14 不同构建半径下，水声传感器网络的寿命

5.5 算法执行时间比较

栅栏覆盖算法的执行时间不仅取决于算法的优劣，还取决于构建栅栏的数量。为了比较DDHG算法和DPA 算法的优劣，这里只比较构建1-栅栏的算法执行时间。图15比较了随机部署总节点数300，不同构建半径下，采用不同强1-栅栏算法的算法执行时间。该图显示：采用两种算法的执行时间随着构建半径的增大而减少，这是由于构建半径越大，构建栅栏的节点数就越少，节点搜索时间就越短。并且可以看到：采用强1-DDHG 算法的执行时间比强1-DPA 算法的执行时间更短，说明强1-DDHG 算法的速度更快。

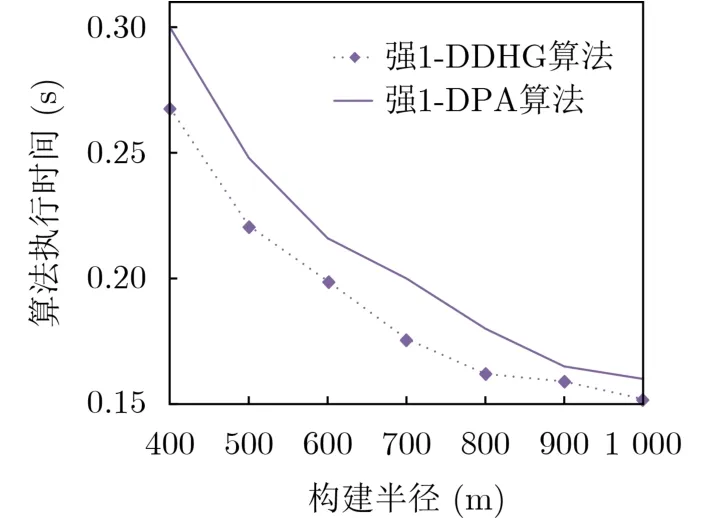
图15 不同构建半径下，算法的执行时间

通过以上仿真结果可以看到：在静态节点的栅栏覆盖中，采用强1-DDHG算法的构建栅栏成功率比采用强1-DPA算法的构建栅栏成功率高。在偏移角一定的情况下，采用强1-DDHG算法所需的传感器数目比采用强1-DPA算法少，并且强1-DDHG算法的运算速度更快。采用强M-DDHG算法构建的平均栅栏数比采用强M-DPA算法构建的平均栅栏数大。当采用多个栅栏共同工作模式时，采用强M-DDHG算法网络的检测概率高于采用强M-DPA算法网络的检测概率。当发射声源级SL=150 dB，偏移角大于60°时，构建半径大于700 m时，采用强M-DDHG算法网络的检测概率可达到95%。

6 结束语

本文通过对有向传感器之间位置关系的讨论，明确了两个有向传感器之间建立连接关系的条件。以此条件为基础构建覆盖图并进行分级，基于分级图能够以尽可能少的节点对静态有向传感器网络进行首次栅栏覆盖。本文提出的强1-DDHG算法的栅栏构建成功率比强1-DPA算法栅栏构建成功率高，构建栅栏所需的节点数比强1-DPA算法少，运算速度比强1-DPA算法快。采用强M-DDHG算法所构建的栅栏数比采用强M-DPA算法多，并且采用强M-DDHG算法时网络的检测概率和网络寿命都优于采用强M-DPA算法时网络的检测概率和网络寿命。因此，在进行静态有向传感器网络栅栏的首次构建时，DDHG算法性能优于DPA算法。但正如文献[14]所述，DPA算法主要适用于移动可旋转有向无线传感器网络的全视野栅栏构建。