新时代供应链低碳转型与效率提升探析
侯小菲
摘 要:本研究借助与碳减排水平存在密切联系的对数函数,以及这一函数的二次Taylor多项式,分析了碳减排水平给低碳产品需求带来的影响,在分析相关数据的基础上,构建出了由一个零售商和一个制造商组建的反映低碳供应链特性的Stackelberg博弈模型,分析制造商碳减排成本、系数、消费者低碳意识给供应链协调、低碳转型以及效率提升带来的影响。但是由于相关数据不足,仍有一些细节需要在后续研究中进行完善。
关键词:新时代;供应链;低碳转型;效率提升
中图分类号:F274 文献标识码:A 文章编号:1005-6432(2024)01-0159-04
DOI:10.13939/j.cnki.zgsc.2024.01.039
为了实现“碳达峰、碳中和”的战略目标,需要落实绿色低碳转型的要求,促进绿色经济发展。企业需要加大低碳技术研发力度,降低生产经营中的碳排放量,遵守国家规章制度,促进企业的绿色发展,制定出科学的发展战略。在“碳达峰、碳中和”战略的推进下,人们的低碳环保意识得到了提升,人们更自觉地购买绿色产品,人们的这些购买行为又推动了企业的绿色低碳转型。
1 相关研究综述
新时代以来,学者们在研究供应链决策协调时,重点分析了那些与“经济理性人”假设不同的决策主体的社会偏好,学者们在后续的研究中得出了新的研究成果,为供应链的实际合作提供了科学的方向。覃艳红等人把供应链成员的利他偏好引入了供应链决策协调模型,发现在需求是线性函数的情况中,供应链整体效率能够得到有效提升[1]。代应等人发现在面临碳减排方面的困难时,零售商利他偏好如果较高,就能够有效提升供应链效率[2]。林强和邓正华结合指数函数的需求,发现了利他偏好水平能够提升对方利润[3]。林强和秦星红在二级供应链Stackelberg博弈模型中引入了利他偏好,证明了电商平台的利他偏好可以提高自身服务水平[4]。
文章在前人研究的基础上,用对数函数替代了线性需求函数中的线性项,这样就能够更科学地描述碳减排带来的影响。借鉴相关研究,设定出了如下的需求函数:D=a-p+ln(1+E),在[0,1]内为E取值,E表示制造商所具有的碳减排水平。文章还构建出了以零售商作为跟随者的Stackelberg博弈模型,分析消费者的低碳意识对碳减排投资、供应链产品定价以及供应链效率的影响。深入探索制造商、零售商的利他偏好给供应链低碳转型协调、决策和效率带来的影响。
2 问题介绍和模型设想
参考前人研究成果,文章假定在碳减排投资成本中,要确保C=k,k>0,这些系数要和碳减排水平存在对应的联系[5]。另外还要确保C′>0,C″>0,在碳减排活动持续进行过程中,改进后续的碳减排技术将会面临较大的难度。消费者在购买低碳产品时不仅看重产品的碳排放水平,而且重视产品本身的绿色低碳属性。在范如国等人的研究中,假定推出低碳产品市场需求函数:D=a-p+tE,其中a表示基本的市场需求,p代表的是零售价格,a和k要大于其他参数,t代表的是消费者所拥有的低碳意识。E是制造商所拥有的碳减排水平,并且满足以下条件:0≤t<1,0≤E≤1。
在这一函数的基础上,能够证实消费者所对应的消费偏好,可以提高低碳产品的市场需求。然而在这一函数中,碳减排水平E和碳减排产品的需求之间存在线性关系。但是在市场活動中,E给市场带来的影响并不能出现线性关系。其他的碳产品所具备的碳减排水平可以给市场需求带来巨大的影响,表现出边际贡献递减的特点。当制造商在早期减少碳排放时,碳排放减少量可以有效提高消费者的购买意愿,进一步提升产品市场需求,然而在推进碳减排的过程中却面临着产品市场需求拉动变小的问题。把E的线性项tE变成对数函数,这样可以更精准地描述出碳减排水平给产品市场需求带来的影响。E的范围是[0,1],在通常情况下,碳减排能够给产品市场需求带来正向的影响,所以可以把对数函数项设成ln(1+E), 把需求函数转变为D=a-p+tln(1+E)。接着假定D=a-p+tln(1+E)能够得到零售商和供应商的一致认可,对于分散决策的情况,制造商来确定w和E,零售商在制造商选出的E和w的基础上,决定最终的p,并结合函数D=a-p+tln(1+E)来制定出最终的订购量q=D。c作为单位生产成本,满足0<c<w<p这一条件,所以可以得出零售商、制造商、供应链的利润,具体内容如下:
πr=(p-w)(a-p+tln(1+E))(1)
πm=(w-c)(a-p+tln(1+E))-kE22(2)
πsc=(p-c)(a-p+tln(1+E))-kE22(3)
3 供应链决策分析
3.1 集中决策情形
面临集中决策这种形式,要制定出科学的决策目标,确保供应链整体利润处于最大化程度,把上文中的式(3)对p、E来求偏导数,让偏导数为0,可以得到以下的式(4)和式(5)。
πscp=a+c+tln(1+E)-2p=0(4)
πscE=(p-c)t11+E-kE=0(5)
通过式(4)可以进一步得出下式:
p=a+c+tln(1+E)2
然后把式(4)代入式(5),可以得出下式:
a-c+tln(1+E)2t11+E-kE=0(6)
由于1+E≠0,所以可以把式(6)改写成:
(a-c)t+t2ln(1+E)-2kE(1+E)=0(7)
在这一方程式中,未知量E的对数函数无法求解,这种情况给后续研究带来了阻碍。为了清除这一阻碍,可以借助对数函数ln(1+E)的二次Taylor多项式E-E2/2来近似替代ln(1+E),把对应的需求函数转变成D=a-p+t(E-E2/2)。由于d/dE(E-E2/2)=1-E>0,d2/dE2(E-E2/2)=-1<0,因此这一需求函数仍然可以反映出以下特点,即“制造商如果在早期阶段减少了碳排放,那么减少单位产品的碳排放数量可以提升消费者购买欲望,提升低碳产品的市场需求,然而在进一步推进碳减排的过程中,其拉动产品市场需求的效果会变弱”。
当函数为D=a-p+t(E-E2/2)时,可以分别得出零售商、制造商和供应链整体的利润,具体内容如下:
πr=(p-w)a-p+tE-E22(8)
πm=(w-c)a-p+tE-E22-kE22(9)
πsc=(p-c)a-p+tE-E22-kE22(10)
使用E-E2/2取代ln(1+E),然后在集中决策过程中,如何让供应链取得利润最大化的效果,需要满足以下条件:
πscp=a+c+tE-E22-2p=0(11)
πscE=(p-c)t(1-E)-kE=0(12)
由式(11)可以得出:
p=a+c+tE-E222(13)
把式(13)代入式(12)之后可以得到:
a-c+tE-E222t(1-E)-kE=0(14)
在整理之后可以得出和变量E相关的方程:
t2E3-3t2E2+(2t2-4k)E+2(a-c)=0(15)
考虑到方程系数取值的差异,式(15)会有1~3个实根,因为E的取值范围是P[0,1],所以只用在5个点处计算供应链整体利润函数的值就能够实现最优利润,并制定出对应的决策。
3.2 分散决策情形
发挥逆向归纳法的作用,使用E-E2/2来取代ln(1+E), 在分散决策的过程中,让零售商拥有最大化的利润,需要具备以下的条件:
πrp=a+w+tE-E22-2p=0(16)
对式(16)进行求解,可以得出下式:
p=a+w+tE-E222(17)
把式(17)代入式(9),可以得到式(18),如下所示:
πm=(w-c)a-a+w+tE-E222+tE-E22-kE22(18)
实现制造商利润最大化,需要具备以下条件:
πmw=a-a+w+tE-E222+tE-E22-w-c2=0(19)
πmE=(w-c)t(1-E)2+t(1-E)-kE=0(20)
通过解析式(19)可以得出式(20),具体如下:
w=a-a-c+tE-E222+tE-E22(21)
把式(21)代入式(20),可以得出式(22),具体内容如下:
3a-c+tE-E222×3t(1-E)2-kE=0(22)
对上述各式进行整理,可以得出如下的方程式:
t2E3-3t2E2+t2+t(a-c)+4k9E+t(a-c)=0(23)
在通常情况下,式(23)和式(15)不同解,对于D=a-p+t(E-E2/2)这种函数,使用批发价契约的方法,难以取得二级供应链协调的效果。当给定了契约参数时,可以按照上述方法进行计算,分别计算分散决策情形和集中决策情形下各供应链成员的效率和利润。
4 利他偏好给供应链效率带来的影响
结合上述关于供应链成员利他偏好的分析[6],文章按照利他偏好供应链的相关特点,分别构建出了零售商和制造商所对应的效用函数,具体内容如下:
ur=(1-βr)πr+βrπm
um=(1-βm)πm+βmπr(24)
在这个函数中,ur、um表示零售商和制造商所对应的效用函数,βr、βm代表的是供应链成员的利他偏好系数。当βr比较大的时候,零售商利他偏好一般也会较大,这时零售商会更加关心供应商利润;当βm比较大的时候,制造商一般也会有较大的利他偏好,这能够说明制造商更关心零售商的利润能力。在现实的供应链合作中,成员企业往往会更看重自身的利润,文章假设0≤βr≤0.5,0≤βm≤0.5。在特定的利他偏好假设中,制造商和零售商在做出决策的过程中,不再只从最大化利润函数的角度进行分析,而侧重于最大化效用函数。在进行供应链集中决策时,需要重点围绕供应链整体的利润函数来实现最大化效果。在制造商和零售商具备利他偏好的情况下,当供应链成员开展集中决策活动时,最优价格、最优碳减排水平和自利型供应链存在一致的关系,当进行分散决策时,制造商和零售商使用的策略以及所采用的求解方法,和自利型供应链的求解方式具有相同的特点[7]。
首先,本研究用MATLAB软件对制造商和零售商的供应链效率和均衡策略进行仿真模拟,全面分析利他偏好给各成员带来的影响。在自立型供应链这种情况中,批发价格所对应的契约参数值如下:c=1、a=15、k=10、t=0.3,当利他偏好系数表现为:βr=0.1、βm=0.1时,使用MATLAB软件对Stackelberg博弈模型进行求解,可以得出制造商对应的批发价格是w*=8.3761,对应的碳减排水平是E*=0.1075;零售商利润π*r=10.4661,p*=10.357,制造商利润π*m=26.5373,供应链利润π*sc=38.1040,制造商利润u*m=24.7500,零售商利润u*r=12.2645,供应链效率r=0.6550。通过比较分析可以发现,制造商碳减排水平提升了0.0124,批发价格提高了0.3625,制造商利润提升了2.8883,供应链效率提高了0.0239,零售商价格下降了0.1718,零售商利潤下降了1.6213。从这些数据中可以发现,利他偏好给各成员的均衡决策以及零售商、制造商、供应链整体效率和利润都带来了巨大影响。
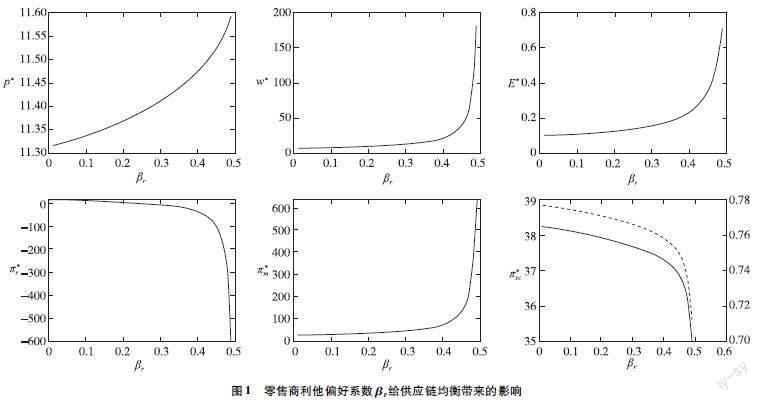
其次,在其他參数固定的情况中,零售商的利他偏好给其他成员的均衡决策、效率和利润带来巨大影响[8]、。在利他型供应链发挥作用的过程中,相关参数值如下:c=1、a=15、k=10、t=0.3,βm=0.1,βr变化的范围是(0.01,0.49),步长对应的数值是0.01,使用MATLAB软件对Stackelberg博弈模型进行求解,可以得出制造商的批发价格和碳减排水平、供应链整体的效率和利润、零售商所对应的零售价格,进而绘制出关系图(如图1所示)。通过图1可以发现,制造商的批发价格w*,制造商所对应的碳减排水平E*,零售商所对应的零售价格p*,都随着βr的上升而下降。在βr在(0,0.5)范围内上升的过程中,刚开始的时候,供应链所对应的整体利润π*sc、零售商所对应的利润π*r以及供应链整体所对应的效率r呈现出缓慢下降的趋势;在βr不断接近0.5的时候,供应链所对应的整体利润π*sc、零售商所对应的利润π*r以及供应链整体所对应的效率r表现出迅速下降的趋势。βr在(0,0.5)范围内上升的过程中,在刚开始的时候,π*m呈现出缓慢上升的现象;在βr不断接近0.5的过程中,π*m的上升速度比较快。
最后,通过分析图中的变化趋势,可以发现提高零售商的利他偏好,并不能对制造商、零售商和供应链整体利润进行帕累托改进。尤其是在零售商利他偏好系数βr提升的过程中,零售商所对应的利润在变化过程中逐渐转为负值。
图1 零售商利他偏好系数βr给供应链均衡带来的影响
在以上分析的基础上,当制造商所对应的利他偏好系数βm得到提高时,供应链成员的利润能够得到有效提升,供应链效率也会得到提高。在本研究中的供应链模型中,如果零售商利他偏好较小,那么制造商利他偏好会变大,结合这二者的特点,可以提高供应链效率。
5 结语
在新时代,促进供应链低碳转型与效率提升,能够促进经济可持续发展,满足广大人民群众日益增长的美好生活需要。结合以上分析,文章认为如果在利他型供应链中,制造商占据了主导地位,需要确保零售商拥有一定的理性,制造商需要合理地提升利他偏好水平,给零售商一定的优惠,鼓励零售商做出科学的订货决策,逐渐对各方利润完成帕累托改进。
参考文献:
[1]覃燕红,艾兴政,宋寒.利他偏好下基于批发价格契约的供应链协调[J].工业工程与管理,2015,20(2):109-115,121.
[2]代应,林金钗,覃燕红,等.利他偏好下低碳供应链批发价格契约协调机制[J].计算机工程与应用,2017,53(11):252-259.
[3]林强,邓正华.利他偏好下基于批发价格契约的供应链协调[J].数学的实践与认识,2018,48(14):129-138.
[4]林强,秦星红.基于利他偏好的电商供应链最优决策与契约协调[J].数学的实践与认识,2021,51(4):287-299.
[5]吴正祥,李宝库.利他偏好下需求依赖于价格和营销努力的两级供应链决策与协调[J].中央财经大学学报,2017(12):108-118.
[6]范如国,林金钗,朱开伟.基于批发价格契约的低碳供应链协调研究——考虑互惠和利他偏好的分析视角[J].商业研究,2020(6):46-54.
[7]王一雷,朱庆华,夏西强.基于消费偏好的供应链上下游联合减排协调契约博弈模型[J].系统工程学报,2017,32(2):188-198.
[8]KOHLER S.Altruism and fairness in experimental decisions[J].Journal of economic behavior & organization,2011,80(1):101-109.

