广义五阶非线性薛定谔方程的怪波与呼吸子的复合波解
董浩楠,扎其劳,2
(1.内蒙古师范大学 数学科学学院,内蒙古 呼和浩特 010022;2.内蒙古自治区应用数学中心,内蒙古 呼和浩特 010022)
广义五阶非线性薛定谔方程是描述一维海森堡铁磁自旋链的模型。近年来有较多关于广义五阶非线性薛定谔方程的研究成果,包括对广义五阶非线性薛定谔方程的一类精确解[1]、N-孤子解[2]、N-暗孤子解[3]、高阶怪波解[4]和周期怪波解[5]等。
关于复合波的相互作用解有一定的研究基础,文献[6]通过使用修正的达布变换讨论了怪波与呼吸子相互作用解的动力学行为;文献[7]讨论了具有两个高阶离散算子的广义非线性薛定谔系统的怪波与呼吸子的相互作用。本文进一步尝试构造广义五阶非线性薛定谔系统的怪波与呼吸子的复合波解。
1 广义五阶非线性薛定谔方程
对于广义五阶非线性薛定谔方程[8]
其中
方程(1)的Lax 对为
其中
其中λ是复特征值。方程(1)的经典达布变换是特殊的规范变换
通过式(3),方程(2)可以得到新的Lax 对
其中U[1],V[1]与U,V在方程(3)中有相同的形式。矩阵中的q和s被q[1]和s[1]替换。U[1],V[1]满足
这里T[1]=λI-S[1],其中
Φ1[0]=(φ11[0],φ21[0])T是方程(3)在q=q[0]和λ=λ1的特殊解。也是方程(3)在q=q[0]和λ=的特解。根据式(6),可以得到方程(1)的一重达布变换
当λ=λk(k=1,2,…,N),Φk=(φ1k,φ2k)T是方程(3)的基础解。N重达布变换通过一重达布变换迭代得到。关于方程(1)的N重达布变换为
这里Φi=(φ1i,φ2i)T(i=1,2,3,…,N) 是方程(3)在λ=λi时的基础解。此处,初值解是Φ1[0]=(φ1i[0],φ2i[0])T=(φ1i,φ2i)T=Φ1。
2 广义五阶非线性薛定谔方程的复合波解
(1)当λ=λj=ihj,得到方程(2)的如下解:
其中
(2)当λ=λr=i,得到方程(2)如下的解:
这里ε是小参数,且sk=mk+nki。令h=1+f2,在f=0(λ=λr=i) 对Φj(λj) 进行级数展开,得
其中,
其中c1,c2,m1,m2是自由参数,也是方程(2)在λ=的解。应用解(12)可以得到怪波解。
利用达布变换,将解(10)和解(12)进行组合,可以得到方程(1)的复合波解。
情形1假设
其中
通过一重达布变换可以得到方程(1)的一阶怪波解
情形2假设
通过二重达布变换可以得到方程(1)的二阶怪波解
通过得到的二阶怪波解,二重达布变换修正为
这里(φ11,φ21)T通过等式(12)(j=1)得到。
情形3假设
在此基础上,通过二重达布变换可以得到方程(1)的一阶怪波与一阶呼吸子的复合波解
情形4通过修正的二重达布变换,将三重达布变换修正为
在此基础上,通过修正的三重达布变换可以得到方程(1)的二阶怪波与一阶呼吸子的复合波解
情形5通过修正的三重达布变换
可以得到方程(1)的一阶怪波与二阶呼吸子的复合波解
3 结论
广义五阶非线性薛定谔方程可以描述五阶、四阶和三阶色散算子光脉冲在非均匀光纤中的传播。本文选择广义五阶非线性薛定谔方程Lax 对的两种特解,应用达布变换给出了该方程的复合解,并详细讨论了怪波和呼吸子之间的相互作用。此外,通过图1-3 展示不同的参数对复合波解的影响。本文的方法具有一定普遍性,可以应用到其它非线性可积系统的求解。

图1 式(23)在γ=δ=α=0.01,λr=i,c1=-5,c2=-5 的一阶怪波与一阶呼吸子的复合波解Fig.1 Hybrid first-order rogue wave and first-order breather with γ=δ=α=0.01,λr=i,c1=-5,c2=-5 of equation(23)

图2 式(25)在γ=δ=α=0.01,λr=i,c1=c2=-5,m1=20,n1=0 的二阶怪波与一阶呼吸子的复合波解Fig.2 Hybrid second-order rogue wave and first-order breather with γ=δ=α=0.01,λr=i,c1=c2=-5,m1=20,n1=0 of equation(25)
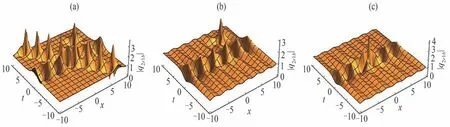
图3 式(27)在γ=δ=α=0.01,λr=i,h1=0.5 的一阶怪波与二阶呼吸子的复合波解Fig.3 Hybrid first-order rogue wave and second-order breather with γ=δ=α=0.01, λr=i,h1=0.5 of equation(27)
本文通过修正的达布变换方法得到了广义五阶非线性薛定谔系统怪波与呼吸子的复合波解。主要得到解的类型如下:一阶怪波与一阶呼吸子的复合波解、一阶怪波与二阶呼吸子的复合波解、二阶怪波与二阶呼吸子的复合波解。此外,本文还讨论了参数对复合波解不同的影响。研究结果表明怪波和呼吸子可以独立存在于复合波解中。

