磁电弹性材料中圆弧形裂纹的反平面断裂问题

刘欣宇，刘官厅，2

（1.内蒙古师范大学 数学科学学院，内蒙古 呼和浩特 010022；2.内蒙古自治区应用数学中心，内蒙古 呼和浩特 010022）

近年来，随着现代高新技术领域的迅猛发展，磁电弹性材料等相关复合材料的力学、电学和磁学耦合问题的断裂力学的课题研究引起了广大学者的关注，尤其在电子技术、超声技术、传感技术以及其它先进智能结构中得到了广泛的应用［1-4］。磁电弹性复合材料是一种新型的多功能复合材料，不仅可以实现磁能、电能和机械能之间的相互转换，还具有优异的力、电、磁及光学性能［5］。然而，在材料上施加电场或磁场会使材料产生变形，电磁器件在使用过程中受到机械、电/磁载荷的作用而导致的应力集中会促使裂纹的产生和扩展，最终将导致部件失效［6］。因此，国内外许多学者在电磁材料断裂特性及强度性能等方面进行分析和研究。

Gao 等［7-8］基于Eshelby-Stroh 公式得到椭圆孔的通解，并分析了无限大电磁材料中单个裂纹和共线裂纹问题，得到了应力强度因子和电磁场的显式解。Chen［9］考虑了热磁电弹材料动态断裂的能量释放率和与路径无关的积分问题。Guo 等［10］在电、磁不渗透情况下，研究了磁电弹性固体中圆孔产生的多裂纹的反平面问题。Rogowski［11］考虑了电磁弹性耦合介质中椭圆孔边含有两个不对称裂纹的反平面问题，结合复变法与保角映射法，求得了场强因子和能量释放率的解。王玮华［12］分析了电磁弹体中正三角形孔边裂纹和椭圆孔边四条不等长裂纹的问题，求解出了场强度因子、能量释放率的解析表达式。刘鑫等［13］利用保角变换技术，研究了磁电弹性材料中的唇形裂纹的反平面问题。郭怀民等［14］提出利用复变函数方法解决了磁电弹性体中的唇形运动裂纹问题。刘鑫［15］引入施瓦兹保角映射，利用复变函数法和叠加原理，研究了电磁弹体中螺形位错与斜裂纹相互作用。Hu 等［16］研究了在反平面剪切载荷和面内磁电载荷共同作用下的电磁弹体与正交各向异性半空间的界面裂纹问题。杨东升等［17-18］借助Gurtin-Murdoch 表面理论和保角变换技术，研究了磁电弹性材料中含有带四条纳米裂纹的正4n形纳米孔的反平面断裂问题，并利用Cauchy 积分公式，针对磁电弹性压电材料中椭圆带四条裂纹的反平面问题进行了研究。

刘又文等［19］首次将不同弹性材料界面共圆弧裂纹版平面问题化为解析函数边值问题，进而获得了一般解及几种典型情况下的应力强度因子；随后基于复变函数的解析延拓技术与奇性主部分析法，针对反平面集中力作用下的不同弹性材料的圆形界面上多条裂纹的问题进行了研究［20］。Wang 等［21］研究了圆形压电夹杂与无界压电基体之间的导电电弧裂纹问题，采用解析延拓的方法，将边值问题化为标准Riemann-Hilbert问题，结果发现裂尖的应力、应变、电位移和电场均具有振荡奇点。曾芸芸［22］构造了圆弧形裂纹的保角映射函数。申大维等［23］提出求解圆弧裂纹问题的新方法，无限大平面弹性体的某一圆周上分布若干条圆弧裂纹，不论无穷远处是否受载荷作用，都可化成求解一个复势函数边值条件的线性关系问题。基于此法，求得了无穷远处受双轴拉伸时圆弧裂纹问题的精确解，进而获得应力强度因子和位移场以及圆弧裂纹面上的位移。皮建东等［24］对一维六方准晶中的圆弧裂纹以及抛物线裂纹的反平面剪切问题进行了研究。郑明明等［25］针对含有两个圆弧裂纹电致伸缩材料的平面问题，应用复变函数方法，获得了在电场作用下复势函数的解析解和应力强度因子的精确解。但是，对磁电弹性材料中含有的穿透型圆弧裂纹缺陷，在磁电全非渗透及全渗透边界条件下的反平面问题，目前尚未见报道。本文研究磁电弹性体中圆弧形裂纹在无穷远处受到沿磁电极化方向的磁/电载荷和反平面机械载荷的共同作用下的反平面问题，借助保角映射技术和复变函数方法，得到了应力场及位移场的精确解析解，以及在磁电全非渗透及全渗透边界条件下，裂纹尖端场强度因子和能量释放率的解析解。

1 磁电弹性材料反平面问题的基本方程

关于x3轴对称的二维横观各向同性磁电弹性材料，取x3轴为磁电极化方向，选垂直于x3轴的x1ox2平面为各向同性面，在远场加载条件下，二维反平面问题中的反平面的位移u(x1，x2)、面内电势φ(x1，x2)和磁势ψ(x1，x2)相互耦合，简化后的本构方程为

其中k=1、2，所有场分量均只是坐标x1和x2的函数。

磁-电-弹三场平衡方程为

应变-位移关系为

磁-电梯度方程为

其中，重复下标表示求和，下标中的逗号表示对相应坐标求偏导；σij、Di、Bi分别表示应力、电位移和磁感应强度；u、φ、ψ分别表示位移、电势和磁势；cijkl、κik和μik分别表示弹性刚度、介电常数和磁通率张量；ekij、qkij和dik分别表示压电、压磁和磁电耦合常数；fi、fe和fm分别表示单位体积体力、体电荷密度和体电流。

若不考虑体力、体电荷密度和体电流的作用，即fi=0，fe=0 和fm=0，则

因为矩阵A是非奇异的，所以式（3）等价于

2 磁电全非渗透情况

2.1 问题描述及求解

假设无限大横观各向同性磁电弹性介质中包含一穿透型圆弧形裂纹缺陷（图1），取圆弧裂纹两端点连线为x1轴，x2轴穿过裂纹中点，设圆弧所在圆的圆心在ic处，圆弧所对应的弦长为2a，弓高为h。

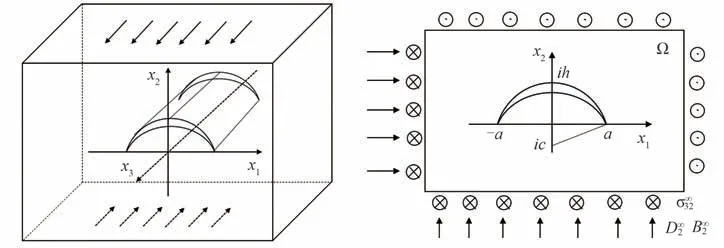
图1 磁电弹性材料中含有穿透型圆弧形裂纹Fig.1 Magnetoelectroelastic material with a penetrating circular arc crack

考虑无限大横观各向同性磁电弹性介质中含有圆弧形裂纹的反平面问题。在无穷远处受到沿磁电极化方向的磁、电、弹作用。由线弹性理论，可转化为在无穷远不受作用，而仅在圆弧形裂纹的表面上受到沿极化方向的磁、电、弹作用，其边界条件为

根据复变方法，调和方程（7）的解u3k、φ、ψ可表示为任意三个解析函数f1(z)、f2(z)、f3(z)的实部，令

并且z=x1+ix2，Re 表示复变函数的实部，且对任一复函数有

因为fk(z) (k=1，2，3)为解析函数，故有

引入保角映射

则解析函数fk(z) (k=1，2，3)可变换为

经过保角映射，记

根据式（7）、（9）-（15）有

位移和应力均可以由fk(z) (k=1，2，3)表示，当在一定的边界条件下求得fk(z) (k=1，2，3)时，即可确定问题的位移场以及应力场。

为了求解上述边值问题，引入保角映射［22］

其中

且|ζ1|＜1，|ζ2|＜1。

该映射将物理平面（z平面）上圆弧形裂纹外部区域Ω 近似地映射到数学平面（ζ平面）上的单位圆γ内部，由点的对应关系可得

将单位圆周γ上的点ζ=σ=eiθ代入式（16），其中ζ为圆内任意一点，并对式（16）等式两边分别乘以后沿单位圆γ积分，结合边界条件（8）得

其中

由于Ψ′k(ζ) (ζ-ζ2)2(k=1，2，3)在单位圆γ内解析，所以有

对保角映射（17）求导得

的边值，因此由Cauchy 积分公式，对于一切|ζ|＜1，有

将式（22）-（27）代入式（20）得到

对式（28）联立求解得到

令方程组（29）中ζ=0，可得

将式（31）代入式（29）的Ψ′k(ζ) (k=1，2，3)中，得

2.2 裂尖处的场强度因子

在式（32）中，令

在裂纹尖端处Ⅲ型场强度因子可定义为

其中ζ′为与裂纹尖端对应的点。由式（23），（33）及（34）可分别求得在裂纹端点z=a和z=-a处的场强度因子。

在z=a处，

在z=-a处，

2.3 讨论

当a保持不变，而h→0 时，圆弧形裂纹退化为Griffith 裂纹，且在z=a处的场强度因子为

在z=-a处的场强度因子为

以上所得结果与文献［2］的结果一致。

2.4 能量释放率

对于磁电全非渗透型裂纹，其能量释放率公式为［10］

将式（35）和（36）分别代入式（39）中，得到用场强度因子表示的能量释放率。

在z=a处，

在z=-a处，

其中

以上在磁电全非渗透边界条件下的结果与文献［13］结果一致。

3 磁电全渗透情况

对于磁电全渗透边界条件可表示为［25］

由此，得到磁电全渗透边界下场强因子的解析表达式，在z=a处，

在z=-a处，

将式（45）和（46）代入式（39），当z=a时

当z=-a时

以上在磁电全渗透边界条件下的结果与文献［13］结果一致。

4 数值算例与讨论

为了讨论圆弧形裂纹的几何参数对场强度因子的影响，以及磁电全非渗透及磁电全渗透边界条件下几何参数、力、电和磁载荷对能量释放率的影响，本文考虑一种特殊磁电弹性复合材料BaTiO3-CoFe2O4，以压电材料BaTiO3为夹杂，以压磁材料CoFe2O4为基底混合而成。磁电弹性复合材料BaTiO3-CoFe2O4相关的材料常数选取见表1。

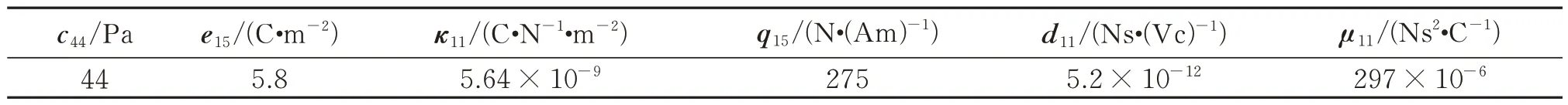
表1 磁电弹性复合材料BaTiO3-CoFe2O4 材料常数Tab.1 Material parameters of magnetoelectroelastic BaTiO3-CoFe2O4 composite

能量释放率的临界值Gcr=5.0 N/m，设=3 Mpa；=0.01 C/m2；=0.001N/Am。

在z=a处，无量纲场强因子K*随圆弧形裂纹半弦长与弓高比值a/h的变化曲线如图2 所示。由图2可知，随着半弦长与弓高比值a/h的不断增大，场强度因子呈现增大的趋势，并且数值增大的速度由快至慢逐渐放缓。当a/h无限增大下去时，即a保持不变，h→0 时，圆弧形裂纹退化为Griffith 裂纹，此时场强因子将会呈现最大值。

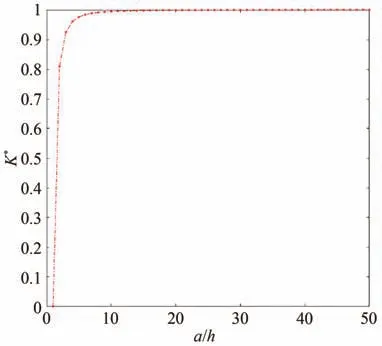
图2 无量纲K* 随a/h 的变化Fig.2 Variation of dimensionless K* with a/h

在z=a处，能量释放率G/Gcr随磁电全非渗透及磁电全渗透边界条件下远场机械载荷τ∞32的变化关系如图3 所示。从图3 可以看出，在磁电全渗透边界条件下，当机械载荷τ∞32的绝对值增加时，能量释放率会随之增大，这表明机械载荷的增加会促进裂纹的扩展；在磁电非全渗透边界条件下，当机械载荷τ∞32的绝对值增加时，能量释放率呈现先减小后增大的趋势，这表明随着机械载荷的不断增加最终还是会对裂纹的扩展起促进作用。

图3 G/Gcr 随 的变化Fig.3 Variations of G/Gcr with

在z=a处，能量释放率G/Gcr随磁电全非渗透及磁电全渗透边界条件下电载荷及磁载荷的变化关系如图4 和图5 所示。在磁电全渗透边界条件下，能量释放率是一个恒定的值，即电载荷及磁载荷的变化对能量释放率没有影响；在磁电全非渗透边界条件下，磁载荷对能量释放率的影响和电场相类似，正负磁/电场可以使能量释放率减小或增大，即磁/电载荷既可以抑制又可以促进裂纹扩展。这表明负磁场或正负电场都会抑制裂纹的扩展，然而正磁场会促进或阻碍裂纹的扩展，具体情形主要与所施加的机械载荷以及磁场或电场强度的组合有关。

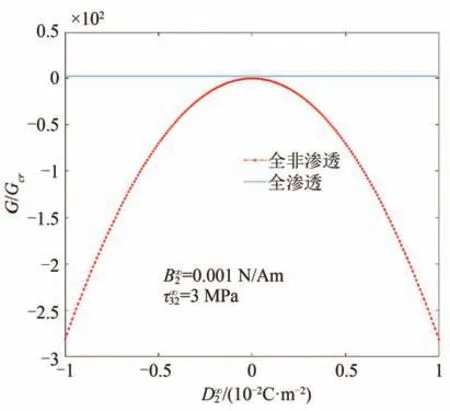
图4 G/Gcr 随的变化Fig.4 Variations of G/Gcr with

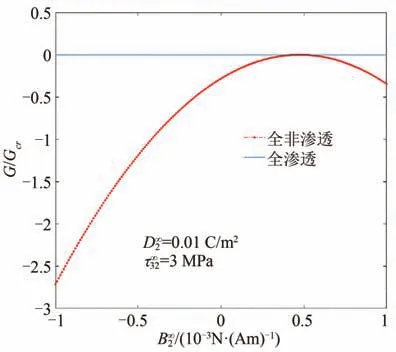
图5 G/Gcr 随的变化Fig.5 Variations of G/Gcr with

5 结论

本文建立了磁电弹性体中含有的穿透型圆弧形裂纹在无穷远处受到沿磁电极化方向的磁/电载荷和反平面机械载荷的共同作用下的断裂力学模型。通过充分利用保角映射技术和广义复变函数理论得到了该问题的应力场及位移场的精确解析解，并同时获得了在磁电全非渗透及磁电全渗透边界条件下，分别在圆弧裂纹的z=a处以及z=-a处的裂纹尖端场强度因子和能量释放率的解析解。基于解析解并利用数值算例，分析了构型断裂失效的影响因素并进一步得到许多有用的结论，这些结论可以在工程实践中提高电磁器件性能以及评估其工作寿命提供理论基础与指导意义。

（1）随着圆弧形裂纹半弦长与弓高比值a/h的增加，会引起裂尖处的场强度因子的增大，并且其增大的速度由快至慢逐渐放缓。另外，当a/h无限增大，即a保持不变，h→0 时，圆弧形裂纹退化为Griffith 裂纹，此时场强因子将会呈现最大值。

（2）在磁电全非渗透及磁电全渗透边界条件下，机械载荷对能量释放率的影响相类似，即随着机械载荷的不断增加，最终还是会促进裂纹的扩展。

（3）在磁电全渗透边界条件下，能量释放率是恒定值，即电载荷及磁载荷的变化对裂纹扩展不产生影响，但与材料常数和机械载荷的大小水平有关；在磁电全非渗透边界条件下，正（负）磁电载荷的增加会阻碍裂纹的扩展。