考虑多因素的致密砂岩气藏不同井型气水产能预测新模型

尹 霜, 李艺恬, 赵 锐, 湛祥惠, 李雨桓, 凌晓杰

(1.中国石油化工股份有限公司上海海洋油气分公司勘探开发研究院, 上海 200120;2.中国石化胜利油田分公司海洋采油厂, 山东 东营 257000;3.中国石油天然气股份有限公司西南油气田分公司川东北气矿, 四川 达州 635000; 4.中国石油化工股份有限公司西北油田分公司, 乌鲁木齐 830011)

跟随着中国油气勘探开发程度的加深,非常规油气资源的关注度逐渐增加。在各种非常规气中,为中国天然气产量提供重要支撑的主要是致密砂岩气[1]。研究表明,中国致密砂岩气可采资源量为8.8×1012～12.1×1012m3,是目前我国最为现实的待开发非常规气资源[2]。

致密砂岩气藏由于孔喉狭窄,渗流时易形成水化膜而产生启动压力梯度[3-6];渗流过程中微小的应力改变会对致密储层渗透率造成较大影响,使得致密储层存在着比低渗储层更明显的应力敏感效应[7-11];加之气水关系多样,生产时,气层含水使得气体渗流启动压力梯度增大、应力敏感效应增强,大大降低气井产能[12-16]。致密砂岩气藏多采用压裂开采且压裂井型多样[17-18]。多种复杂因素的影响使得致密气藏气井的产能较难确定,因此,明确以上因素对致密砂岩气藏压裂井产能的影响具有十分重要的意义。

针对致密气特殊的渗流特征,许多学者提出了多种产能预测模型[19-26],但多数模型仅针对直井或水平井等单一井型,压裂斜井的相关模型较少;且综合考虑启动压力梯度、应力敏感、气井产水等因素研究较少。

基于此,本文以致密气藏压裂直、斜、水平井为对象,研究启动压力梯度、应力敏感、气井产水等多个因素对产能的影响,基于稳定渗流理论,利用保角变换、水电相似原理等,分别建立适用于致密砂岩气藏压裂直井、压裂水平井及压裂斜井的气水两相产能预测模型,并分析各因素对致密砂岩气藏压裂井产能的影响。

1 压裂井理论模型及假设条件

1.1 压裂井理论模型假设条件

压裂井产能预测模型假设条件为[27,30-31]:①压裂井均位于均质、等厚、等温、各向同性、顶底封闭气藏中心;②压裂井采用射孔完井,产层完全打开,直井垂直裂缝沿井眼对称分布,水平井压裂缝垂直于井筒,沿井筒对称分布,裂缝无限导流且与气层等高,流体流动顺序为基质→裂缝→井筒;③流体为气水两相均质流体,水相不可压缩,渗流过程为等温稳态渗流且无任何特殊的物理化学现象发生;④考虑储层应力敏感以及气水两相启动压力梯度的影响;⑤不考虑裂缝、地层及近井筒地带污染,不考虑井筒压降,忽略重力及毛管力的影响。

据以上假设条件,设地层厚度为h,地层原始渗透率为ki,泄气半径re对应的压力为pe,井底流压为pwf,井筒半径为rw,压裂井裂缝半长为Lf,缝宽为Wf,水平井及斜井裂缝条数为N,斜井井斜角为θ,斜井段长度为L。

1.2 压裂直井产能预测模型

以理论模型假设条件为基础,构建压裂直井物理模型(图1)。将压裂直井渗流划分为两阶段,即基质椭圆流(以裂缝端点为焦点)和裂缝线性流(图2)。

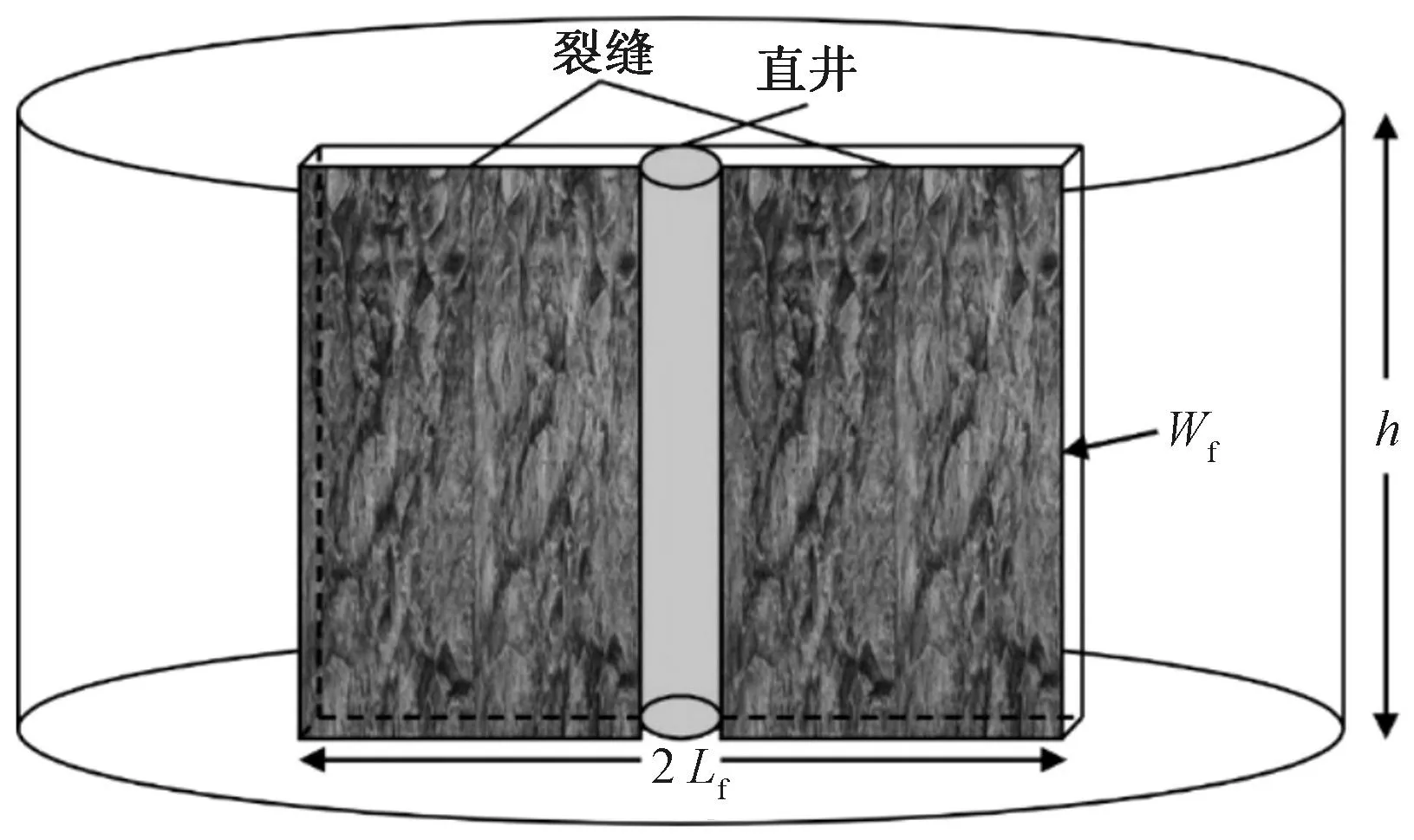
图1 致密气压裂直井物理模型示意图

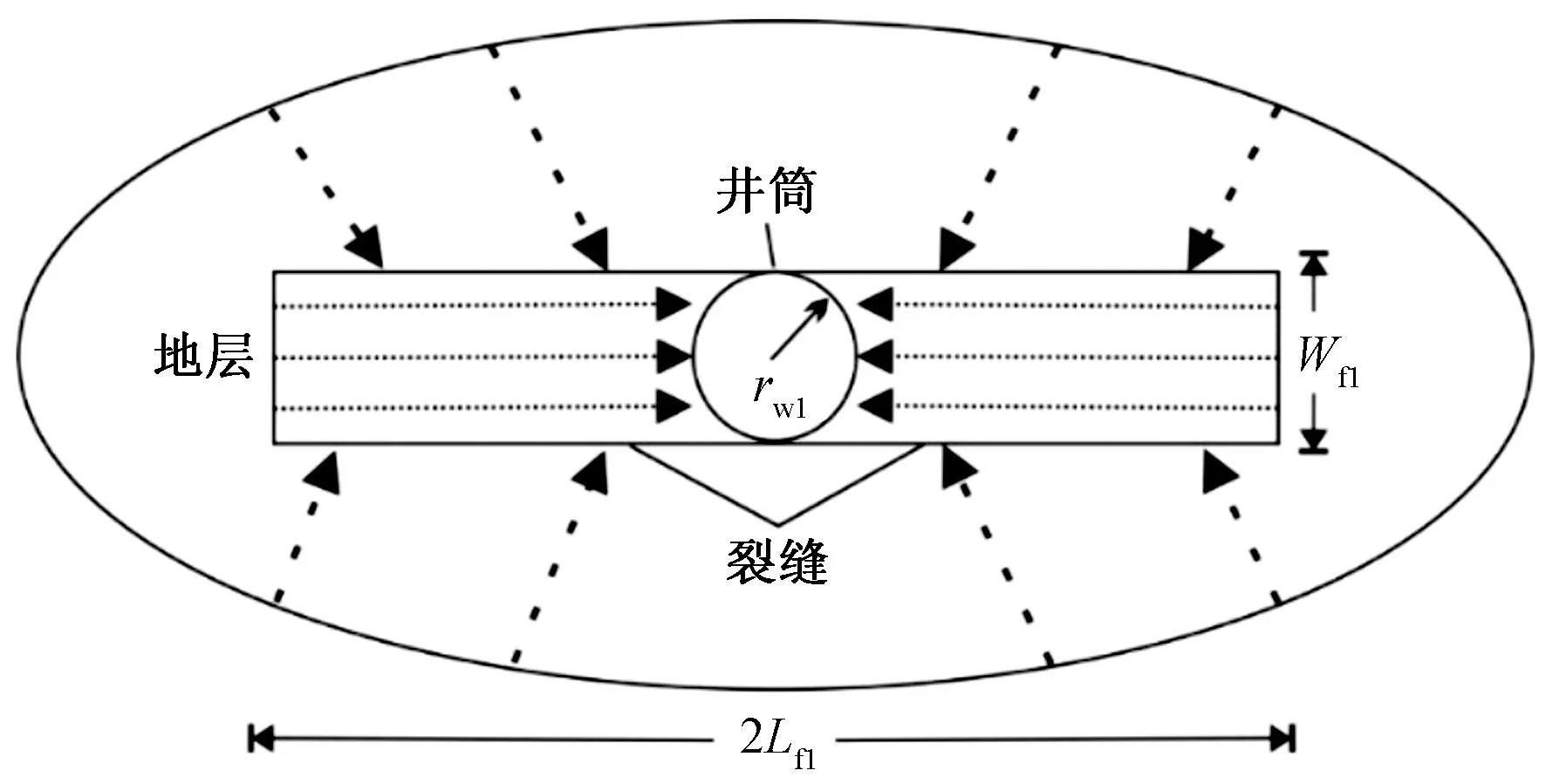
图2 致密气压裂直井地层及裂缝渗流过程示意图

1.2.1 基质渗流模型

针对地层中椭圆渗流部分,可利用保角变换,将裂缝椭圆渗流场变换为等价的直井平面径向渗流场。因此,首先推导考虑启动压力梯度及应力敏感效应的气水平面径向流模型。根据稳定渗流理论,可得气、水流动方程:

(1)

(2)

联立式(1)和式(2),分离变量并移项,有

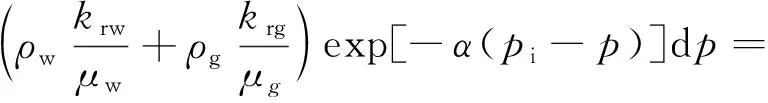
(3)

设地层两相拟压力为

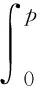
(4)

设地层两相拟启动压力为

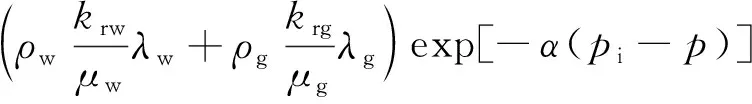
(5)

设水气两相体积流量比WGR为

(6)

将式(6)代入式(3),积分得

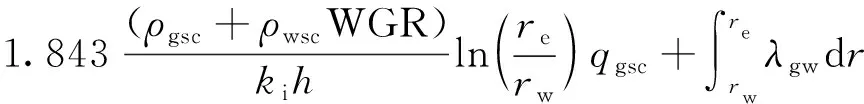
(7)

式中:pe为边界压力(MPa);pwf为井底流压(MPa);pi为原始地层压力(MPa);ρgsc为地面标况下气体的密度(g/cm3);ρwsc为地面标况下水相的密度(g/cm3);WGR为生产水气比(m3/104m3);ki为地层原始渗透率(mD);k为地层渗透率(mD);h为地层厚度(m);re为泄压半径(m);rw为井筒半径(m);qgsc为地面标况下气相的体积流量(m3/d);qwsc为地面标况下水相的体积流量(m3/d);ρg为地层条件下气相的密度(g/cm3);μg为气相粘度(mPa·s);vg为地层中气相流速(m/d);krg-地层中气相相对渗透率;μw为水相粘度(mPa·s);vw为地层中水相流速(m/d);ρw为地层条件下水相的密度(g/cm3);krw为地层中水相相对渗透率;λg为气相启动压力梯度(MPa/m);λw为水相启动压力梯度(MPa/m);α为应力敏感系数(MPa-1)。

式(7)为考虑启动压力梯度以及应力敏感的气水两相直井平面径向渗流模型,在此基础上,引入保角变换建立压裂直井基质中产能模型。

假设由垂直裂缝引起的椭圆渗流场长短半轴分别为af、bf,根据式(8)所示保角变换,有

(8)

图3将椭圆渗流场变换为供给半径为(af+bf)/Lf、井径为1单位圆渗流场,可得考虑应力敏感以及启动压力梯度的气水两相压裂直井基质渗流模型为

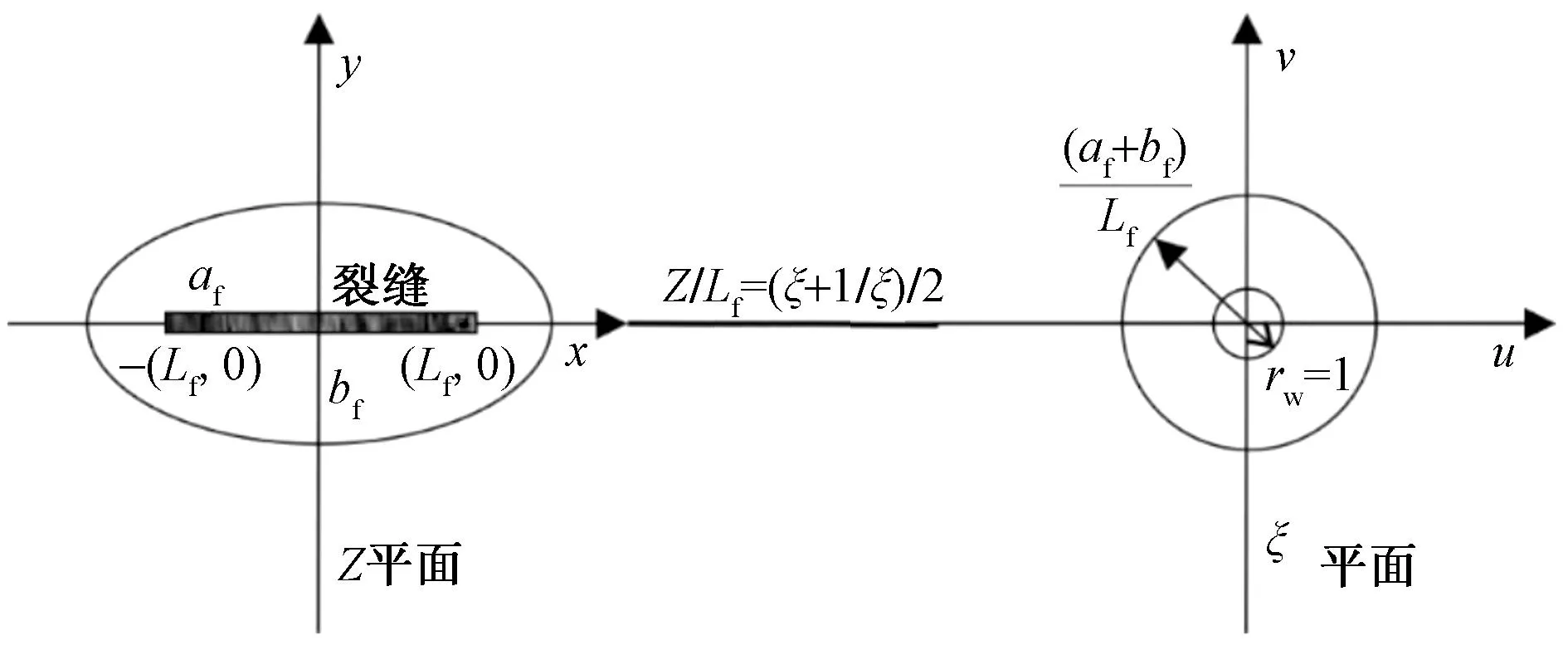
图3 保角变换过程示意图

(9)

式中:

(10)

式中:pf为裂缝尖端压强(MPa);Lf为裂缝半长(m);af为裂缝椭圆渗流场长半轴(m);bf为裂缝椭圆渗流场短半轴(m)。

1.2.2 裂缝渗流模型

直井压裂后形成纵向裂缝,在纵向裂缝中,汇流效应对气体渗流影响较小,因此在裂缝中考虑气体线性流动[28],根据稳定渗流理论,可得压裂直井裂缝中气水两相渗流运动方程分别为

(11)

(12)

联立气水两相运动方程,分离变量并且两边相加,可得

(13)

(14)

从裂缝尖端到井底积分:

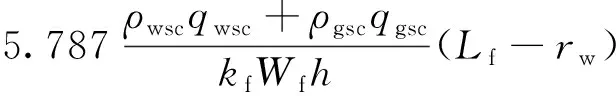
(15)

联立式(7)和式(15),根据水电相似原理,可知两渗流阶段气体流量相等,可得致密砂岩气藏考虑地层应力敏感效应、启动压力梯度的气水两相压裂直井产能方程:

(16)

式中:Wf为裂缝宽度,m。

1.3 压裂水平井产能预测模型

以理论模型假设条件为基础,构建压裂水平井物理模型(图4)。以单条裂缝为研究对象,将压裂水平井的渗流过程划分为地层中以裂缝两个端点为焦点的椭圆流过程以及裂缝中径向流过程(图5)[29]。

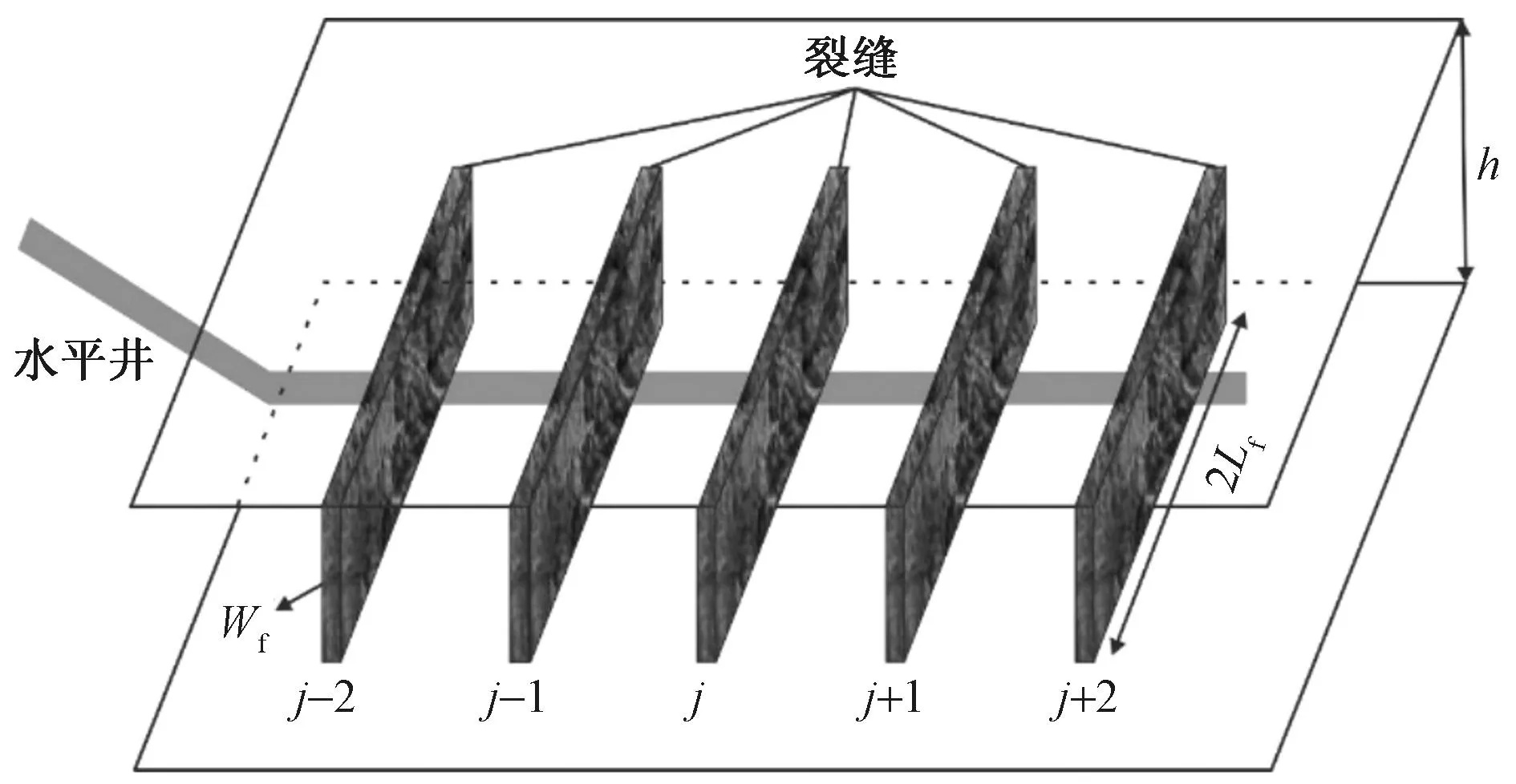
图4 致密气压裂水平井物理模型示意图

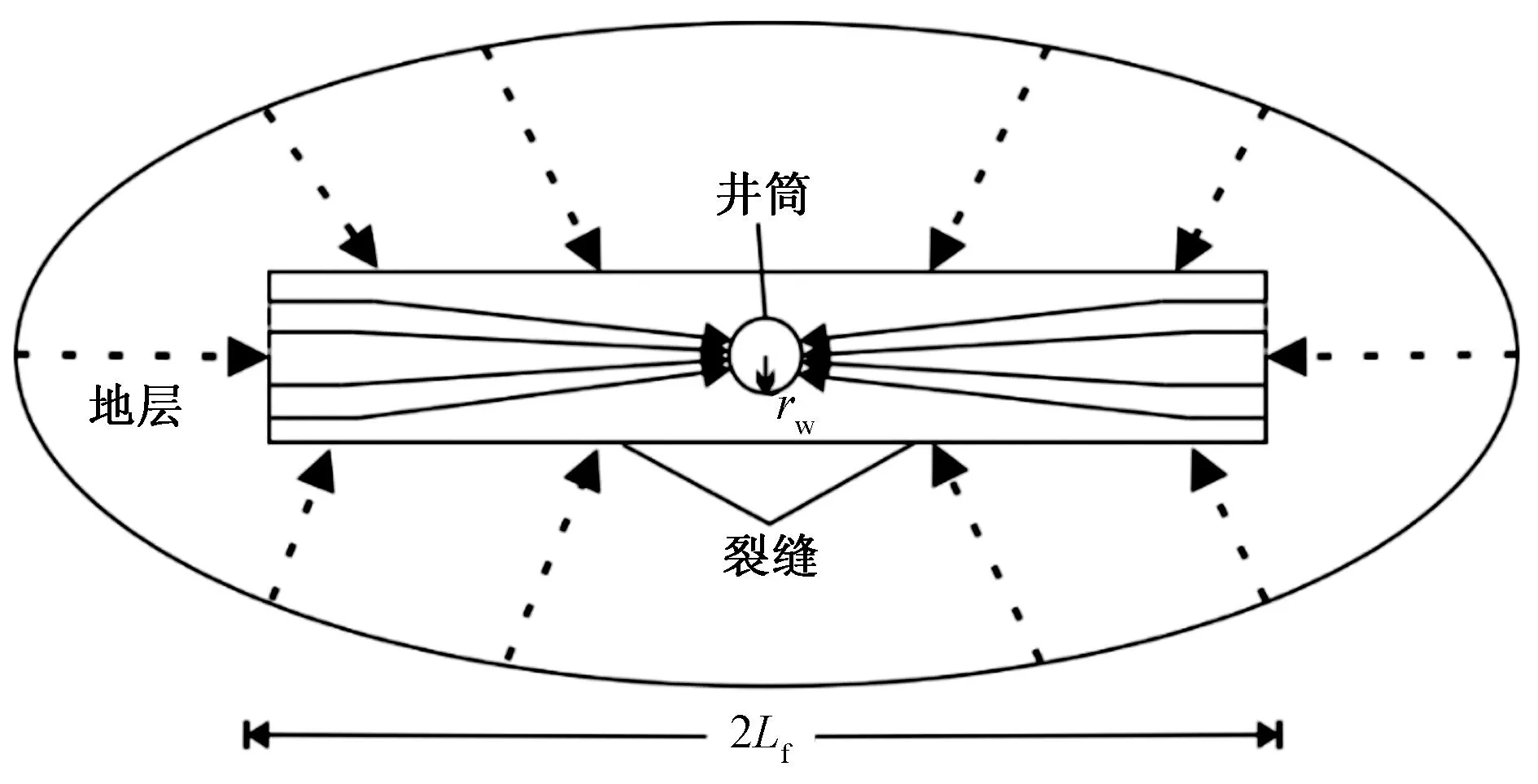
图5 致密气藏水平井地层及裂缝渗流过程示意图

1.3.1 基质渗流模型

当水平井压裂后,气体在地层中渗流发生改变,从而诱发二维椭圆流。与压裂直井相同,引入保角变换,将椭圆流等价为直井径向流,可得压裂水平井基质中考虑应力敏感效应、气水两相启动压力梯度的气水两相模型为

(17)

1.3.2 裂缝渗流模型

(18)

(19)

联立式(18)及式(19),分离变量并移项,有

(20)

(21)

联立式(17)和式(22),根据水电相似原理,可知两渗流阶段气体流量相等,可得致密砂岩气藏考虑应力敏感效应、启动压力梯度的气水两相压裂水平井单条裂缝产能方程:

(22)

N条裂缝总产能为

(23)

式中,N为裂缝条数。

1.4 压裂斜井产能预测模型

以理论模型假设条件为基础,构建压裂斜井物理模型(图6)。以前文推导的水平井模型为基础进行斜井模型的建立,但斜井模型中应加入井斜导致的拟表皮[29]以及裂缝中心和井筒中心并不一致的影响。

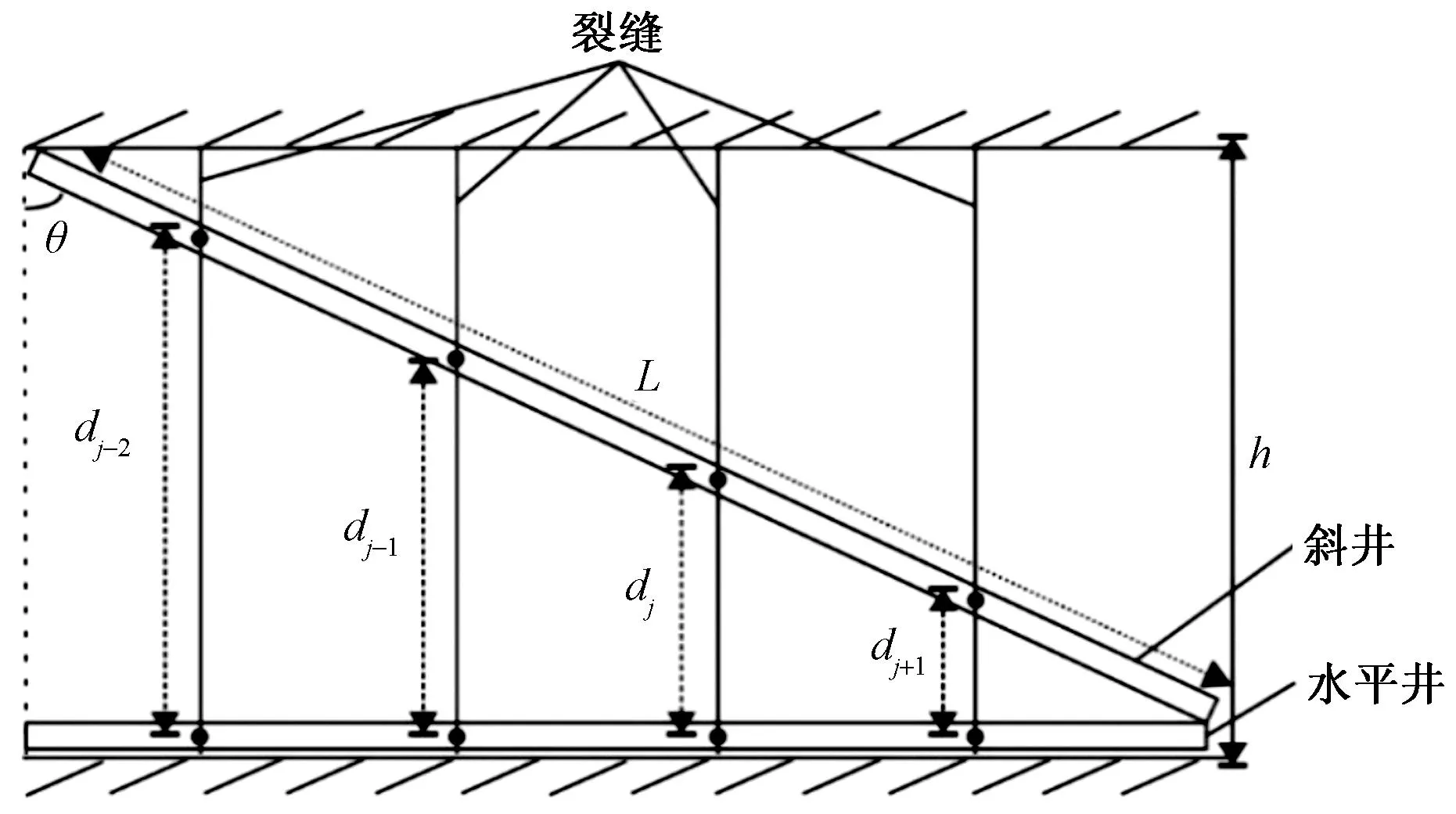
图6 致密气压裂斜井物理模型示意图

1.4.1 基质渗流模型

以单条裂缝为研究对象,气水两相在地层基质中的流动与水平井相同,其产能模型为

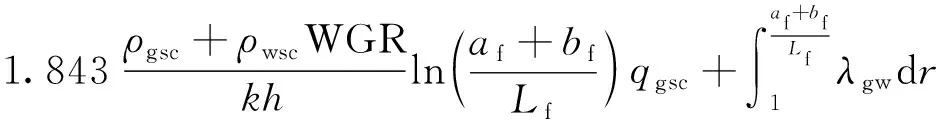
(24)

1.4.2 裂缝渗流模型

针对于裂缝中的流动,井筒倾斜导致压裂缝与井筒相互不垂直,因此,将每条裂缝等效为偏心井,可得其产能方程为

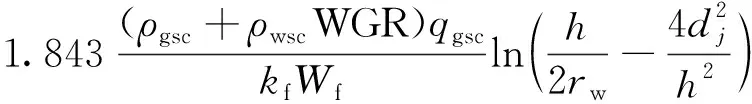
(25)

在式(24)和式(25)基础上,加入井斜导致的拟表皮,可得压裂斜井产能方程:

(26)

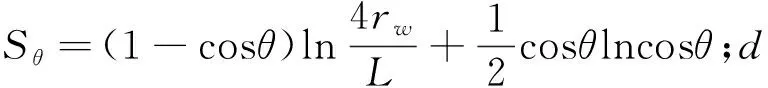
1.5 产能预测模型拟压力函数的求解

将地层水视为不可压缩流体,地层水粘度(μw)、地层水密度(ρw)为常数;通过Lee-Gonzalez方法计算天然气粘度(μg),通过下式计算天然气密度(ρg),公式中天然气压缩因子的计算采用DPR法。

(27)

稳态渗流时,结合水气比定义式及气水运动方程,有

(28)

若假设短时间内水气比WGR保持不变,则首先可由式(28)建立水气相渗比值krw/krg与压力p的关系式;其次通过拟合气水相渗曲线可建立水气相渗比值krw/krg与含水饱和度Sw的关系式;联立上两步操作所得关系式,即可推得压力p与含水饱和度Sw的关系。

鉴于拟压力函数及拟启动压力梯度函数求解过程复杂,因此用梯形公式求解其数值解。

(29)

(30)

2 实例计算及因素敏感性分析

2.1 产能预测模型实例计算

实例计算以四川盆地秋林区块沙溪庙组致密气藏为例。研究区为含局部高点的鼻状构造,河流相沉积为主,中孔、中喉、中分选、较强非均质性储层,87.8%的岩心样品孔隙度<8%、渗透率为0.01～1 mD,属于典型的致密砂岩气藏。各类生产井位于气藏中心部位,均采用射孔完井,模型计算所需相关参数如表1所示,地层、裂缝中气水相渗曲线如图7和图8所示。

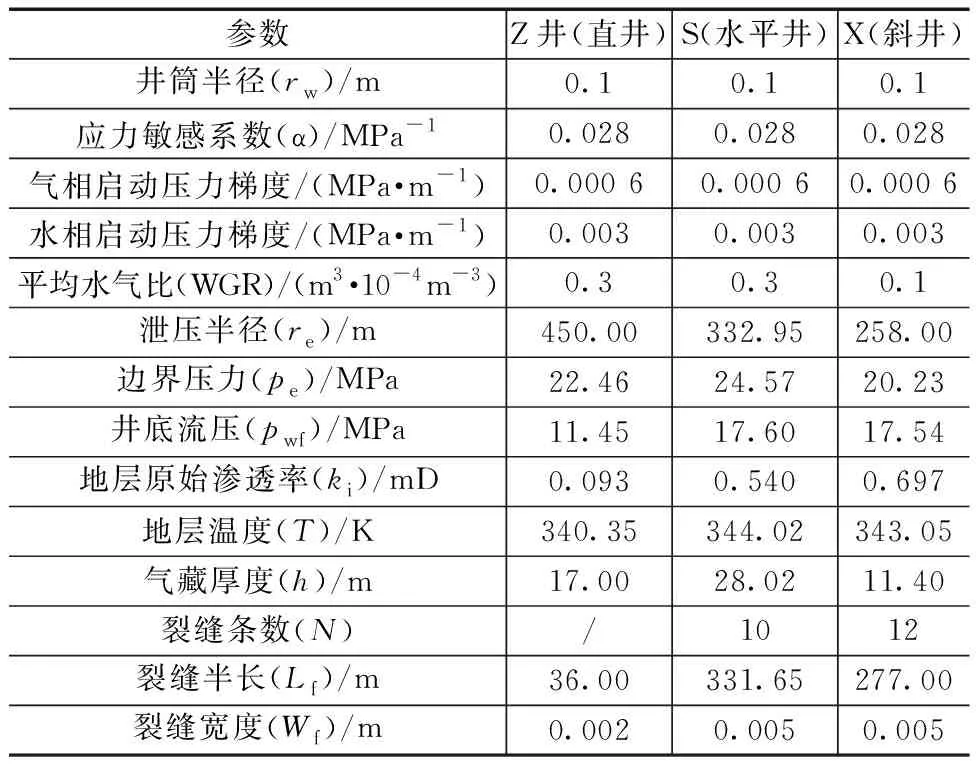
表1 致密砂岩气藏各井型气井基本参数

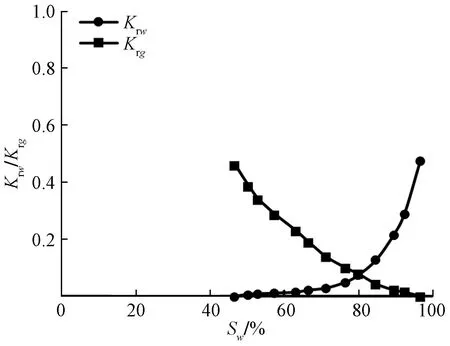
图7 实例气藏地层中气水相渗曲线

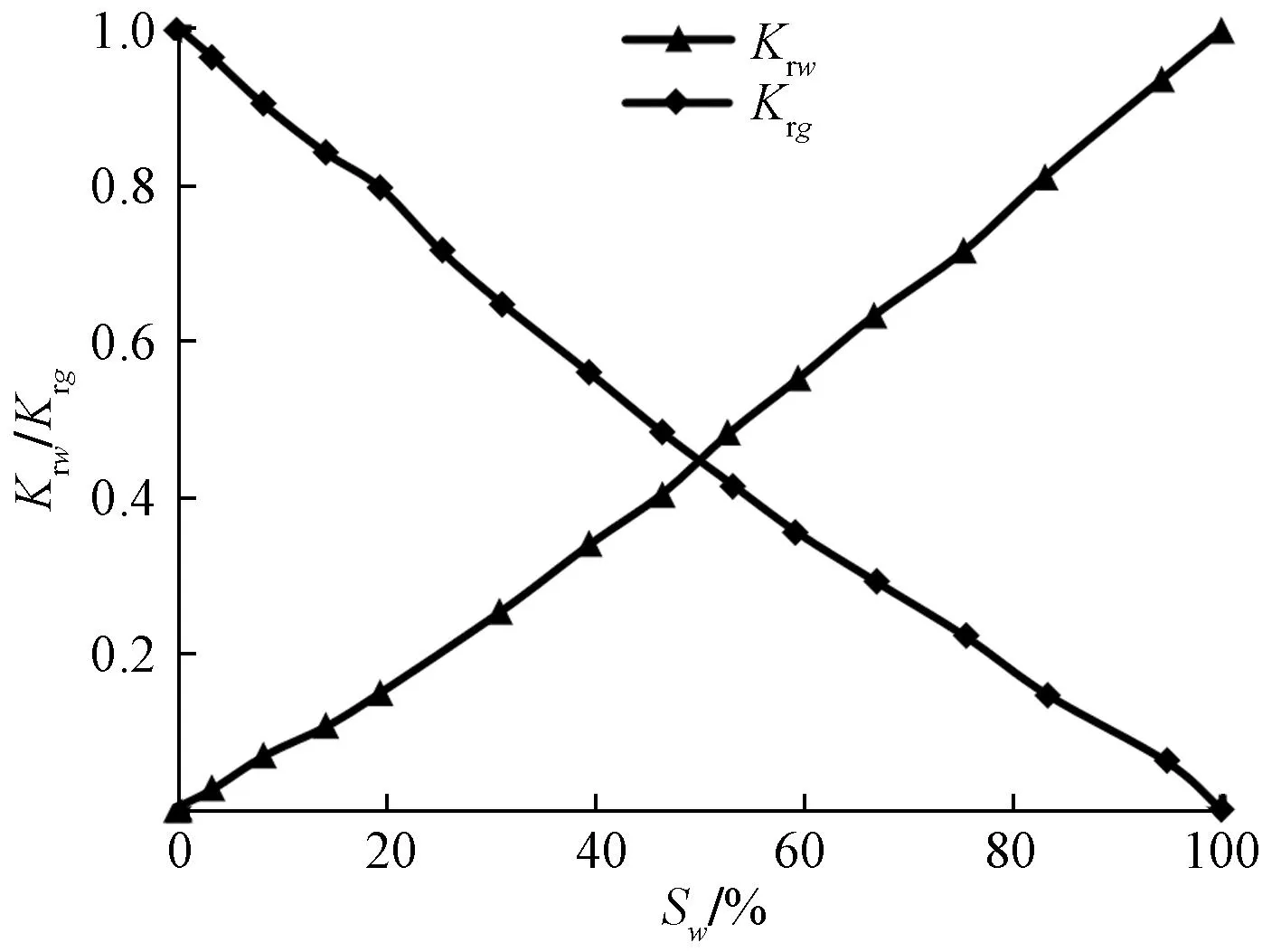
图8 实例气藏裂缝中气水相渗曲线

利用推导的致密砂岩气藏不同井型气水两相产能预测模型预测三类气井的无阻流量,并且与实例中各类气井实测的一点法无阻流量比较,结果如表2所示。由表2可知,通过模型预测的各类气井无阻流量与实测值相近,二者间相对误差百分比均小于5%,属于工程误差范围,表明本文模型能满足现场的需要,能有效地进行产能预测。

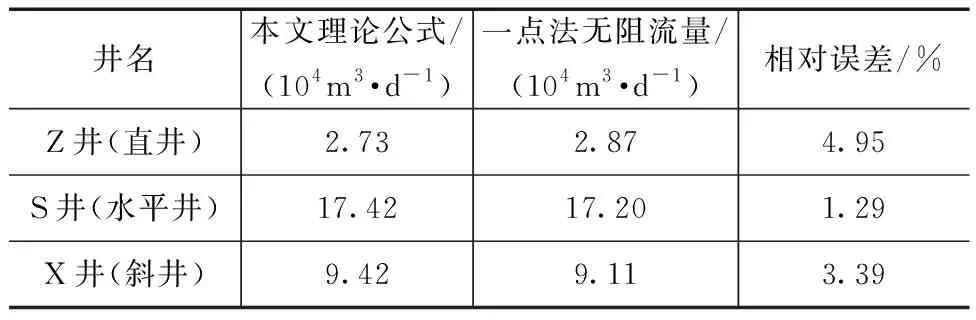
表2 不同井型气水两相产能预测模型计算结果对比

2.2 产能预测模型因素敏感性分析

采用本文推导的产能预测模型,基于上文的实际数据,以压裂水平井B井数据为基础分析不同因素对致密砂岩气藏压裂水平井无阻流量的影响。在分析过程中,采用固定变量的方式,即固定其他参数不变仅调整其中一个参数,通过气井IPR曲线来分析该参数对致密砂岩气藏压裂水平井无阻流量的影响。

2.2.1 应力敏感系数

令除了应力敏感系数(α)的参数保持不变,以0.01 MPa-1为梯度设置4组不同的应力敏感系数,利用本文模型预测相应的IPR曲线,并绘制成图(图9)。由图9可知,应力敏感效应的存在会导致气井无阻流量减小,相应的IPR曲线偏左;随着应力敏感程度的加剧,气井产能降低,曲线左移,但减小趋势有所减缓。当井底流压较小时,应力敏感效应对气井无阻流量存在更大的影响。因此,在气井日常管理过程中,需要将生产压差控制在合理范围之间,减缓应力敏感的影响。

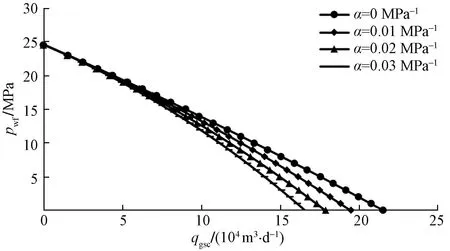
图9 不同应力敏感系数下气井IPR曲线

2.2.2 水气体积比

令除了水气比(WGR)的参数保持不变,以1 m3/104m3为梯度设置4组不同的水气比,利用本文模型预测相应的IPR曲线,并绘制成图(图10)。由图10可知,气井产水导致气井无阻流量降低,相应的IPR曲线偏左;若产气量持续走低并伴随产水加剧会导致气井产能降低,曲线左移,但减小趋势有所减缓。气藏产水后,水相替代气相进入大孔道中,使得气相被切割为不连续状态,水相逐渐占据渗流的优势地位,使得气井产能降低。因此,在在气井日常管理过程中,需优选工作制度,避免见水或延缓气井见水时间。

图10 不同水气体积比下气井IPR曲线

2.2.3 启动压力梯度

令除了气水两相启动压力梯度(λw/λg)的参数保持不变,气相启动压力梯度以0.01 MPa/m为变化梯度,水相启动压力梯度以0.02 MPa/m为变化梯度,设置4组不同的变量,利用本文模型预测相应的IPR曲线,并绘制成图(图11)。由图11可知,气水两相启动压力梯度的存在会导致气井无阻流量减小,相应的IPR曲线偏左;启动压力效应的加剧,气井产能降低,曲线左移。当井底流压较小时,气水两相启动压力梯度对气井无阻流量存在更大的影响;但几条IPR曲线间整体变化不大。因此,气水两相启动压力梯度可做简化处理。

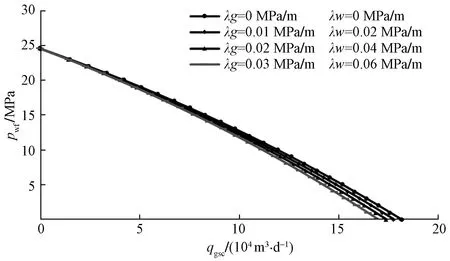
图11 不同启动压力梯度下气井IPR曲线

3 结论

1)针对致密砂岩气藏各类型压裂井渗流特征,基于稳定渗流理论,建立综合考虑应力敏感效应、气水两相启动压力梯度及气井产水的不同类型压裂井气水两相产能方程。利用本文推导的模型计算的无阻流量与实际一点法无阻流量相比误差较小,表明本文模型具有较高的准确性。

2)应力敏感效应及气井产水对致密砂岩气藏压裂水平井产能影响较大,气相及水相启动压力梯度对产能影响较小,可简化处理。在气井日常管理过程中,需要将生产压差控制在合理范围之间,减缓应力敏感的影响,同时采用合理的生产制度避免见水或延缓见水时间。

3)本文提出的不同井型压裂井产能预测对计算参数的准确性依赖较高,计算结果具备参考价值。当计算参数准确时具有较高可信度。