基于附加服务差异化的双寡头航空公司动态竞价演化分析
沈东霞, 赵礼强, 唐金环
(1.沈阳航空航天大学 民用航空学院, 沈阳 110121; 2.沈阳航空航天大学 经济与管理学院, 沈阳 110121)
随着人们物质水平的不断提高,除机票价格外,航空公司提供的服务水平成为了人们出行的新的参考依据,在这竞争日益激烈的航空客运市场中,航空公司提供的附加服务已经成为航空公司的又一主营业务收入。因而如何在实现航空公司互利共赢的前提下,研究附加服务差异化对航空公司价格博弈、市场竞争的影响尤为必要。
据调查显示,我国航空客运运输市场中商务旅客占比超六成,航空公司的服务质量越高,旅客的满意度和忠诚度也会越高。赵桂红等[1]从航空出行旅客选择行为的角度出发,构建我国旅客对附加服务的随机选择模型,研究旅客对附加服务的选择偏好;Zhou和Zhou[2]发现航空公司的服务质量水平对航空公司的收益与发展有着重要的影响;刘聪灵和李程[3]分析了航空公司服务差异下服务成本系数对收益的影响;曹香玲和孙晨赫[4]研究了国内航空公司网络营销策略,提出国内航空公司应分质分价吸引不同目标市场,提升航司品牌形象声誉传播;冯芬玲和李杰潞[5]分析了铁路与公路运输价格和服务质量间的关系及竞争影响。
在航空公司机票价格策略的研究中,一些学者试图找出航空市场竞争的本质,为航空公司的竞争优势提出合理的建议。Li等[6]研究了高铁与航空公司在价格、利润和社会福利上的竞争博弈,分析了航空公司和高铁运营商的最优定价策略;Heywood等[7]发现在具有线性运输成本的寡头竞争模型中,私营企业相较于国营企业会获得更高的收益;谭美容[8]研究了竞争环境下短视和策略乘客并存时航空公司的定价问题,比较价格展示和动态定价模型两种定价策略的收益,给出不同情况下更适合的定价策略;王嵘等[9]通过低成本航空公司主要成本指标与净利润的关联度分析,提出成本控制策略;胡荣和夏洪山[10]通过分析竞争战略与决策理性对航空公司价格竞争的影响,发现竞争战略对其市场竞争行为复杂性有显著的影响,运用延迟反馈控制法可使竞争模型从混沌状态重新回到稳定状态。
航空公司间的竞争是多方参与的博弈竞争,国内的航空客运运输市场属于被少数航空公司占据的寡头垄断市场,大量学者对这类动态竞争的复杂性进行了研究,引入非线性动力学来解释和描述复杂的动力学行为,如稳定性、分岔、混沌等。胡荣和张君[11]讨论了模型均衡点的存在性与稳定性,发现在不稳定时期政府价格调控政策均能使无序的市场竞争趋于有序;Liu等[12]建立了基于非线性可变成本的航空公司竞价博弈模型,探讨了价格调整速度和价格弹性系数对航空公司价格竞争演化规律的影响;Askar[13]研究了企业生产同质产品并采用有限理性规则更新产品的古诺博弈问题,发现整个博弈演化模型只有一个均衡点并研究了该点的稳定性。胡荣和陈圻[14]研究了具有学习能力的有限理性双寡头产量竞争模型,发现混沌控制实施者可以从混沌控制中获利。现有基于航空公司附加服务差异化对收益管理的研究很少,多以调查问卷的形式研究旅客偏好,很少关注附加服务差异化对竞争策略的影响;国内运用非线性动力学研究航空公司动态竞价博弈模型的文献也较少。因此本文从双寡头航空公司的角度出发,分析附加服务差异下航空公司价格竞争策略,通过探讨在多次博弈中航空公司机票价格均衡情况,充分研究航空客运市场的博弈行为,分析附加服务差异对市场需求、收益和竞争的影响,为航空公司实现可持续发展提供更合理的发展策略。
1 航空公司竞价博弈动态模型研究
1.1 基于附加服务考虑的航空公司竞价静态博弈模型
假设航空客运运输市场存在以A、B为代表的双寡头航空公司,两航空公司提供差异化产品并提供各自的附加服务,航空公司机票价格为pi,客流量为qi,其中i=A、B。航空客运运输市场需求函数为
qi=a-βpi+γpj+si
(1)
式中:i,j=A,B且i≠j;参数a>0,表示在不考虑价格影响的情况下,航空公司占航空客运运输市场的规模;参数β>0,表示航空公司的价格敏感系数;γi为航空公司产品差异化系数,通常与航班时刻、航空公司品牌有关,一般而言,参数γi[0,1)且0<γi<β,γi越小,表示航空公司间差异化程度越大,γi=0表示航空公司的产品完全异质;si为航空公司的附加服务水平。假设双寡头航空公司的可变成本具有线性性质,则可变成本函数为Ci(qi)=τiqi,其中τi>0是航空公司的可变成本增加系数,航空公司提供附加服务的利润函数为
πi=(pi-τi)qi-φi
(2)
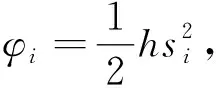
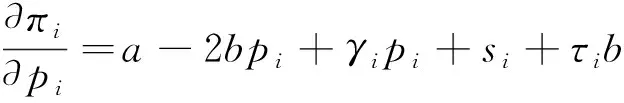
(3)
1.2 航空公司竞价动态博弈模型
由于航空客运运输市场的竞争瞬息万变,航空公司会根据市场动态(节假日、不可抗力因素等)及其他航空公司的实时定价等制定新一轮的定价策略。为了适应多变的航空市场环境,需要引入新的动态博弈模型,将票价调整的动态模型看作一个非线性动力系统,采用有限理性方法对票价进行调整。假设以A、B为代表的双寡头航空公司有限理性,通过重复竞争博弈做出长期定价决策。航空公司将通过估计在T时期的边际利润来调整T+1时期的销售价格,价格的动态博弈模型可表示为
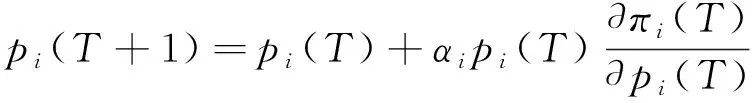
(4)
式中:αi>0,表示航空公司i从T时期到T+1时期的票价调整幅度。双寡头航空公司在每个时期的竞价动态调整过程为
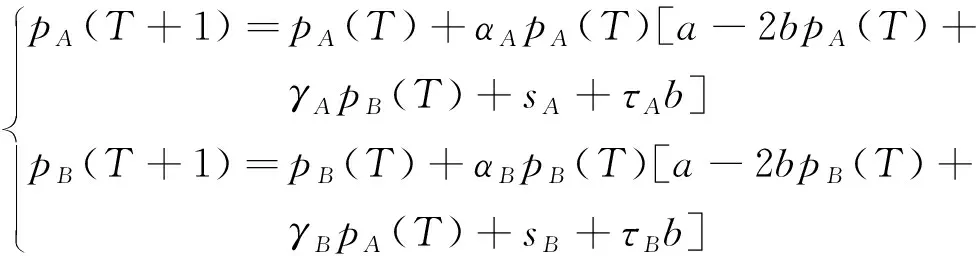
(5)
依据式(5)计算双寡头航空公司博弈均衡点,研究竞价博弈模型的稳定性及均衡点的局部稳定性。
1.3 稳定性分析
若给定pA(T+1)=pA(T),pB(T+1)=pB(T),则式(5)可调整为

(6)
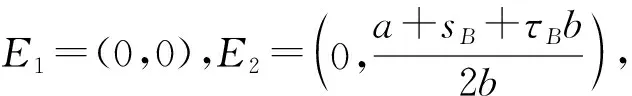
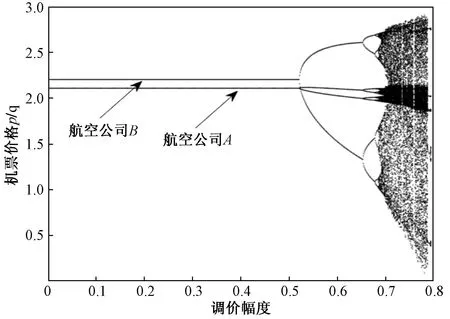
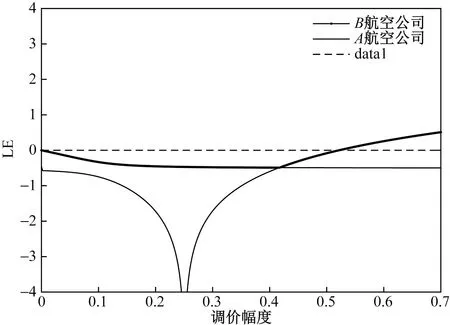
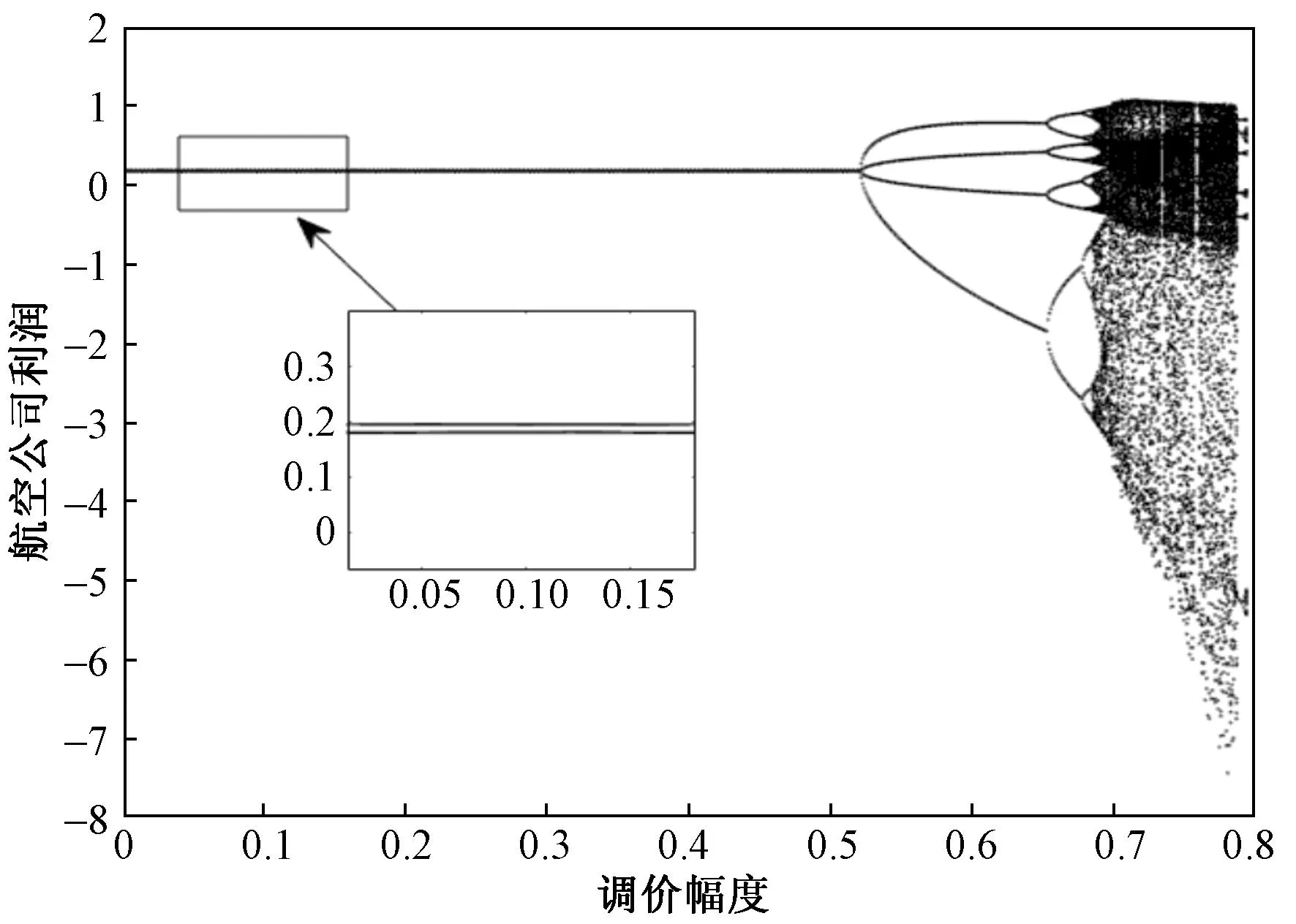
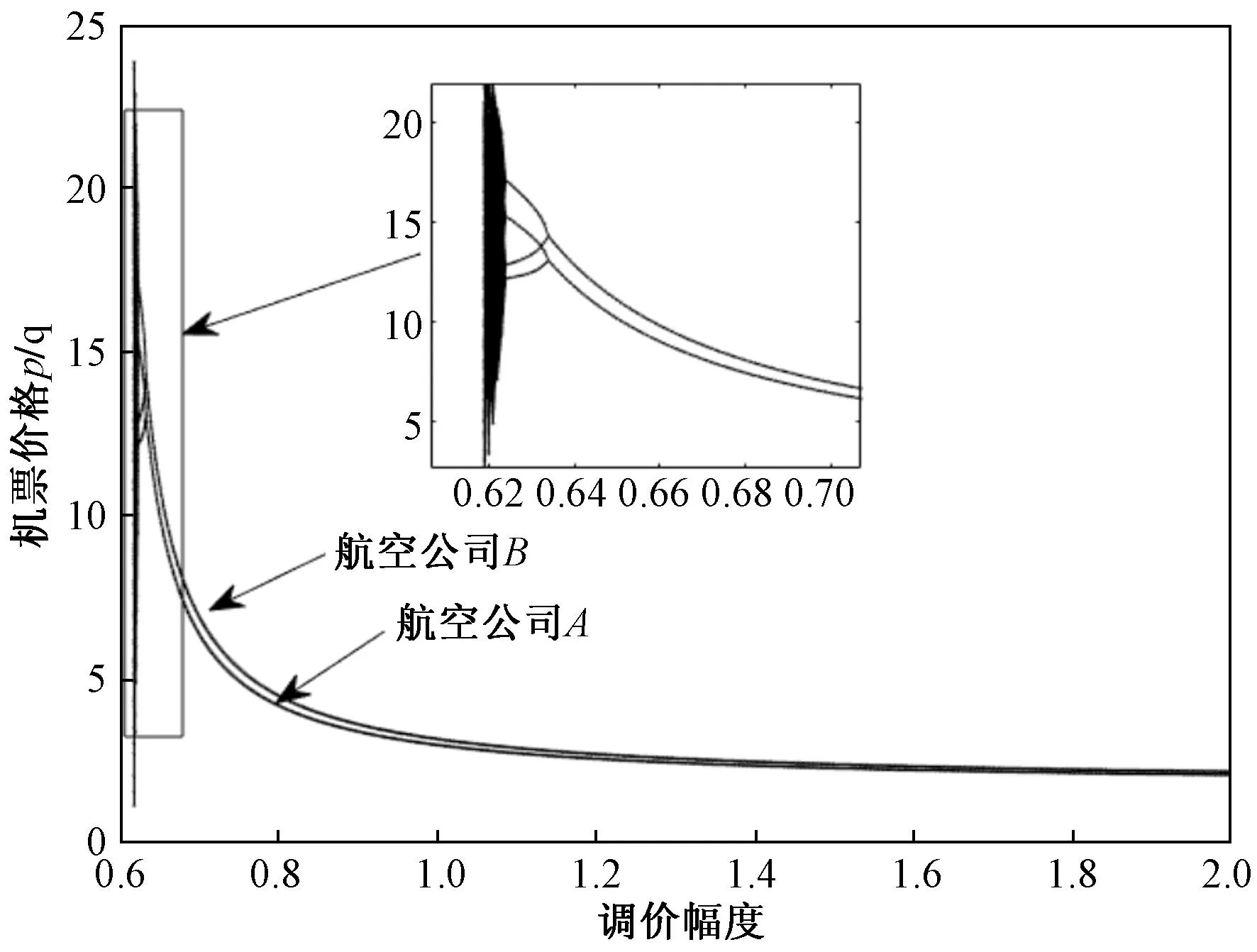
由于参数的非负性及0<γi (7) 定理1:双寡头航空公司竞价动态调整系统博弈均衡点E1为不稳定点。 此时,认为双寡头航空公司都丧失了提供机票买卖的权利,在现实生活中,认为E1为双寡头航空公司同时破产的情况。 在现实生活中,认为E2、E3分别为航空公司A、B单独垄断航空客运市场的垄断均衡解,从经济学角度来说,虽然航空公司一家独大能稳定一段时间的航空市场,但这并不利于市场良性竞争与长期稳定的发展,只有两家或多家航空公司相互制约或相互依存,才更有利于航空市场的健康发展。 证明:略 通常认为E4为两航空公司长期相互竞争的结果,是动态博弈系统的唯一纳什均衡解。 通过上述分析,研究了双寡头航空公司竞价动态调整系统的四个均衡点的稳定性并给出了相应的稳定性条件,接下来将具体讨论双寡头航空公司基于附加服务差异化带来的竞价博弈。 针对双寡头航空公司竞价动态调整系统存在唯一纳什均衡解的情况,分析具有附加服务差异化的航空公司价格竞争策略,假设si=0为航空公司提供附加服务水平低于乘客期望的情况;si>0为航空公司提供附加服务水平高于乘客期望的情况,分情况讨论基于附加服务差异的竞争博弈。 (8) (9) (10) 接下来将通过MATLAB数值仿真考察基于航空公司提供附加服务差异化的有限理性下,非线性双寡头航空公司动态竞价调整模型的稳定性,分析稳定状态下双寡头航空公司的定价与服务策略、系统不稳定的分叉混沌行为以及系统不稳定对航空客运市场的影响,为航空公司制定竞争策略,航空公司实现可持续发展提供更合理的发展建议。 以中国东方航空公司与中国南方航空公司为例,观测2023年3月连续两周的沈阳桃仙机场-新疆地窝堡机场的票价变化,通过查阅民航局行业发展公报及各个航空公司的运营数据,发现两航空公司的旅客市场占比如表1所示。 表1 中国东方航空公司与中国南方航空公司旅客市场占比 由表1可知,根据两航空公司旅客市场的总占比均值,令a=2.1;根据CAPSE(民航旅客服务测评)网站2022年四个季度航空公司服务测评报告,令h=2,b=1.1;通过Brand Finan发布的“全球航空公司品牌价值50强”榜单,基于品牌效应,令γA=0.55,γB=0.45;为剔除新冠肺炎疫情对航空客运市场的不利影响,选取国内两大航空公司2019年的部分财务报表数据,令τA=0.81,τB=0.82。通过观测2023年3月连续两周的沈阳桃仙机场-新疆地窝堡机场票价变化,令航空公司A的票价调整幅度αA=0.122,观测两航空公司的票价设初始市场票价价格为(0.88,1.54)。 随着双寡头航空公司长期复杂的博弈,当系统达到稳定状态时,随着αB的不断增大,系统的均衡票价稳定于(1.731 2,17 923)。当αB=0.499时系统开始出现分叉、混沌(图1),综上可知αB对整个博弈系统的稳定有着至关重要的调控作用,航空公司价格竞争波动过大航空市场处于混乱状态,给航空公司定价决策带来困难。如图2所示,能清晰地观测到系统的稳定性变化。当Lyapunov指数LE<0时,系统处于稳定状态,当LE>0时,系统会进入混沌状态,此时整个航空客运运输市场不稳定。 图1 两航空公司均不提供服务时博弈系统价格竞争分叉 图2 时价格竞争的最大Lyapunov指数 随着两航空公司长期复杂的博弈,如图3所示,当系统达到稳定状态时,随着αB=0.548的不断增大,系统的均衡票价始终保持稳定。当αB=0.548时,博弈系统出现分叉,最终进入完全混沌状态。由图3不难看出航空公司的均衡票价与附加服务水平有关,附加服务水平更高的航空公司的票价要高于不提供附加服务的航空公司。与之对应的Lyapunov指数分析图如图4所示。 图3 航空公司A提供服务时博弈系统价格竞争分叉 图4 时价格竞争的最大Lyapunov指数 由图5可知,随着航空公司票价调整幅度的不断增大,系统的均衡票价始终保持稳定。当αB=0.521时,博弈系统开始2-分岔,4-分叉,最终进入完全混沌状态,此时最大李雅普诺夫指数为正数,整个博弈系统的Lyapunov指数分析图如图6所示。当系统处于混沌状态时对于航空客运市场来说是一种无序的竞争状态,航空公司乱定价使价格处于混沌状态进而使航空公司利润也进入了混沌态。 图5 两航空公司均提供服务时博弈系统价格竞争分叉 图6 时价格竞争的最大Lyapunov指数 如图7所示,在不稳定状态下,过大的调整速度可能会使航空公司的净利润为负,此时航空公司亏损,市场动荡,不利于航空公司健康可持续发展。双方应以此为依据来制定票价实现最大化收益。令αB=0.135 7,将其带入双寡头航空公司均提供附加服务的系统中研究附加服务成本系数h变化时对动态博弈系统的影响,如图8所示。 图7 两航空公司均提供服务时两航空公司净利润的分叉 图8 当时两航空公司关于服务成本系数的博弈系统价格竞争分叉 由图8可知,当h<0.629时,该动态博弈系统不稳定,随着h的增加,系统逐渐稳定且稳定价格趋于均衡票价,因此,航空公司附加服务成本投入过低不利于市场的稳定。 从航空公司提供附加服务差异的角度出发,基于非线性动力学理论来分析双寡头航空公司的动态竞争策略,通过探讨在多次博弈中航空公司间的均衡情况,充分理解和研究航空客运运输市场的博弈行为,利用数值仿真,分析附加服务差异下的均衡解的稳定性范围及附加服务成本对系统稳定性的影响。为航空公司制定竞争策略、政府实行市场监管提供理论依据。研究结果表明: 1)有限理性下非线性双寡头航空公司基于票价动态竞争时,航空公司的调价幅度与附加服务成本对整个博弈系统的稳定性有着至关重要的调控作用,在系统不稳定状态下,随着调价幅度的增大,整个系统会出现分叉与混沌状态,此时航空客运市场动荡,航空公司的利润降低或亏损。附加服务成本投入过低不利于市场的稳定,随着投入附加服务成本的增大系统逐渐稳定,票价趋于均衡票价。因此航空公司竞价博弈期间,应注意附加服务成本的投入,如里程积分兑换,退改签政策,行李托运免费额度控制等,使博弈竞争尽可能地在稳定区域进行,以市场健康稳定为前提寻求最优定价。 2)双寡头航空公司均提供附加服务水平时的票价,比任一方提供或均不提供附加服务水平时的票价要高。因此航空公司应该想办法满足顾客对附加服务的心理预估,如提供机上餐食的多样选择、里程兑换优先值机、城市环线机场大巴等,增加服务的多样性与创新性,提高自家航空公司的收益。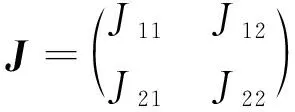
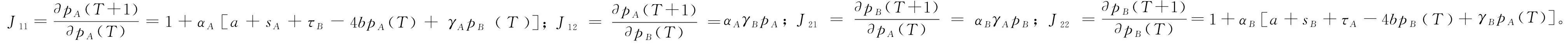

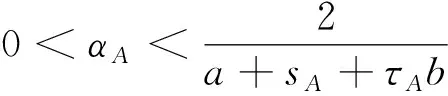
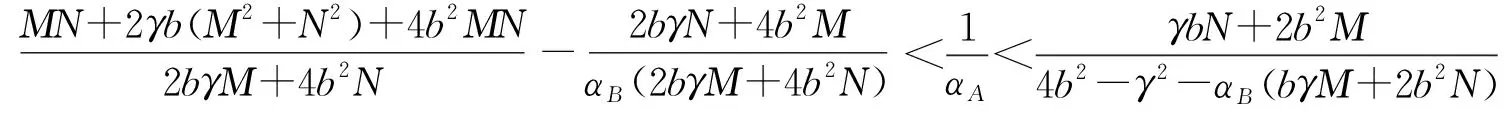
2 基于附加服务差异化的均衡解讨论
2.1 双寡头航空公司均不提供附加服务
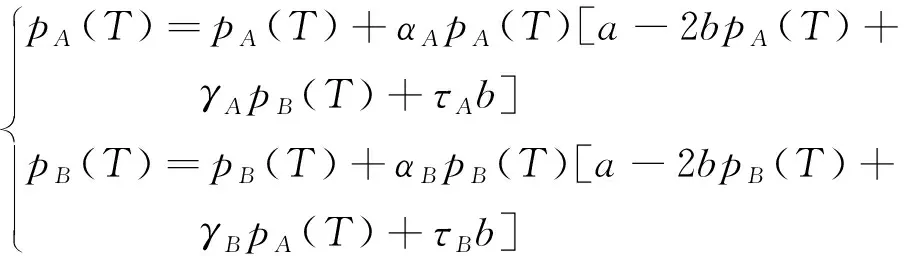

2.2 双寡头航空公司一方提供附加服务


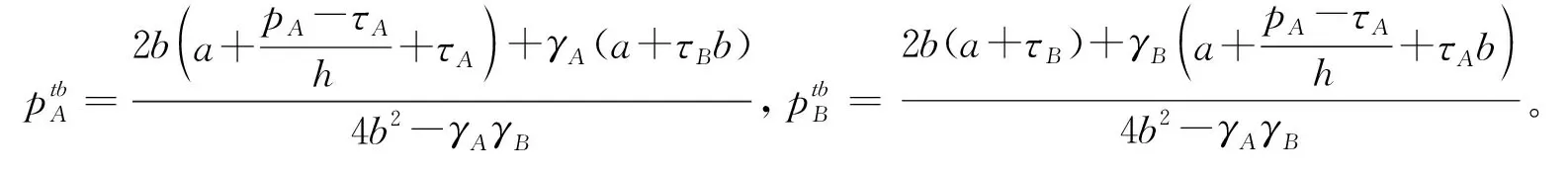
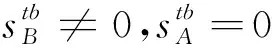
2.3 双寡头航空公司均提供附加服务
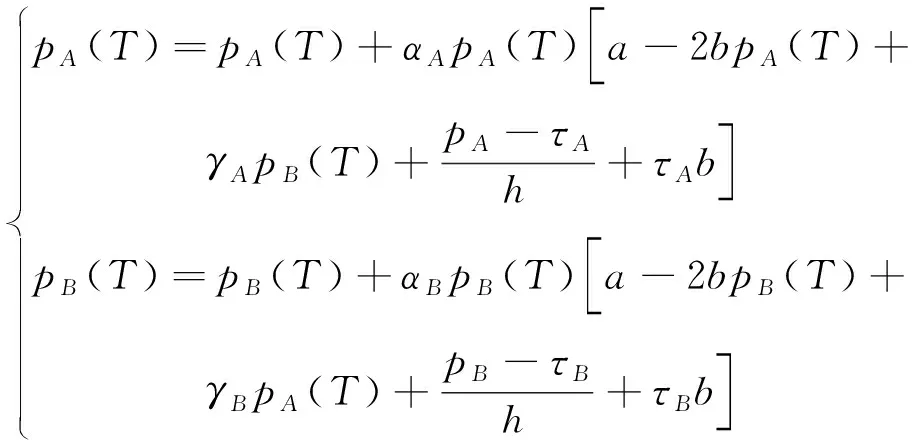
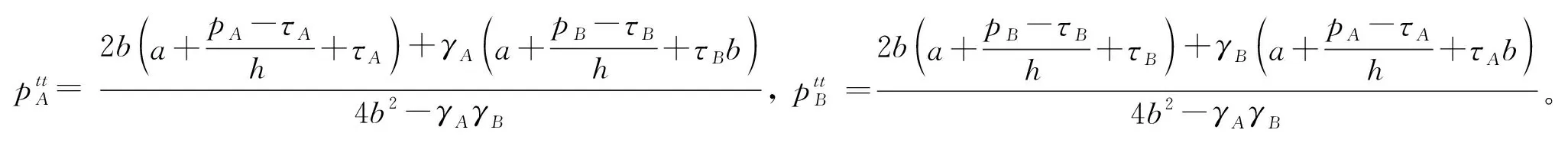
3 数值模拟
3.1 双寡头航空公司均不提供附加服务
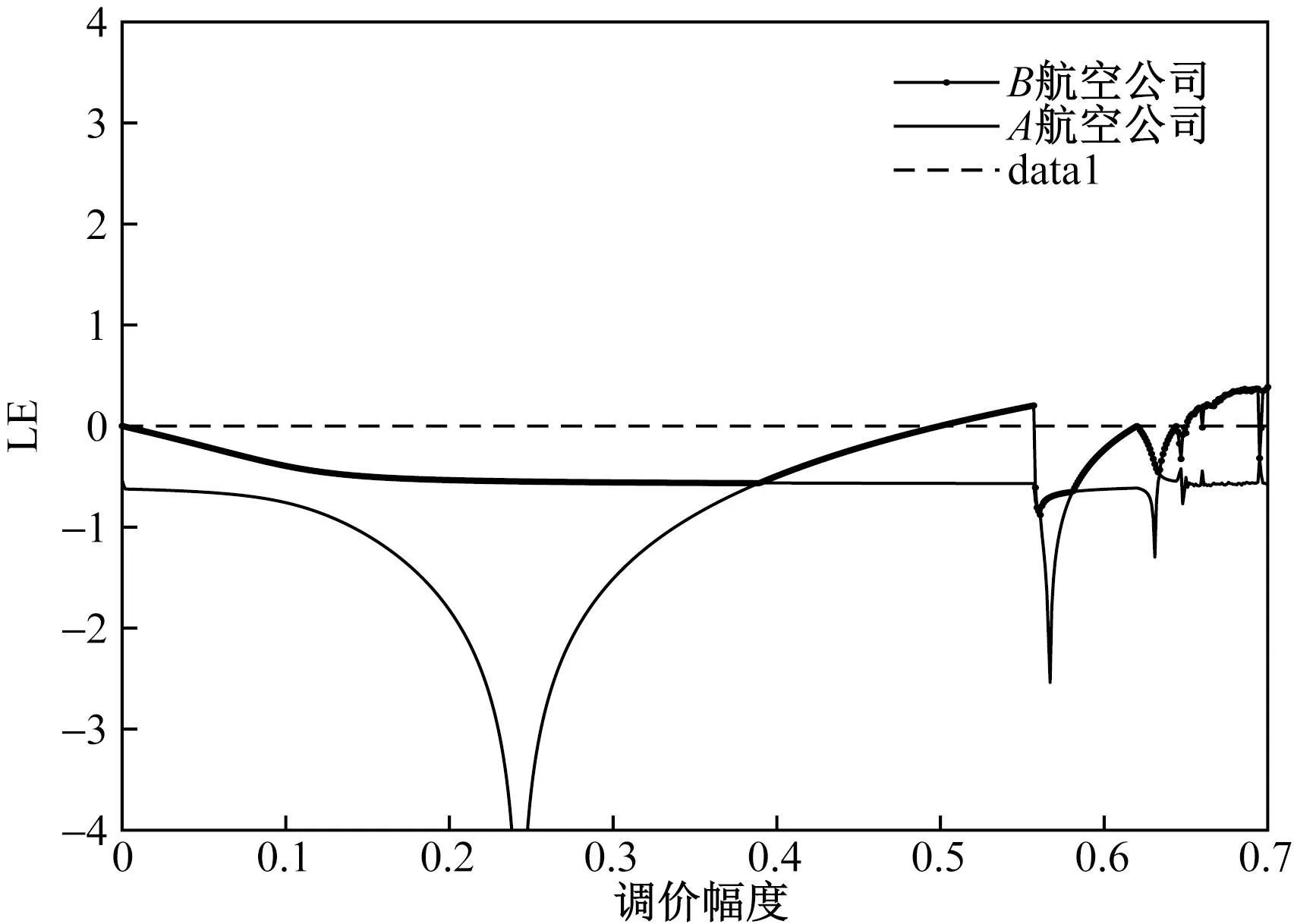
3.2 双寡头航空公司一方提供附加服务
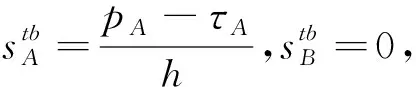
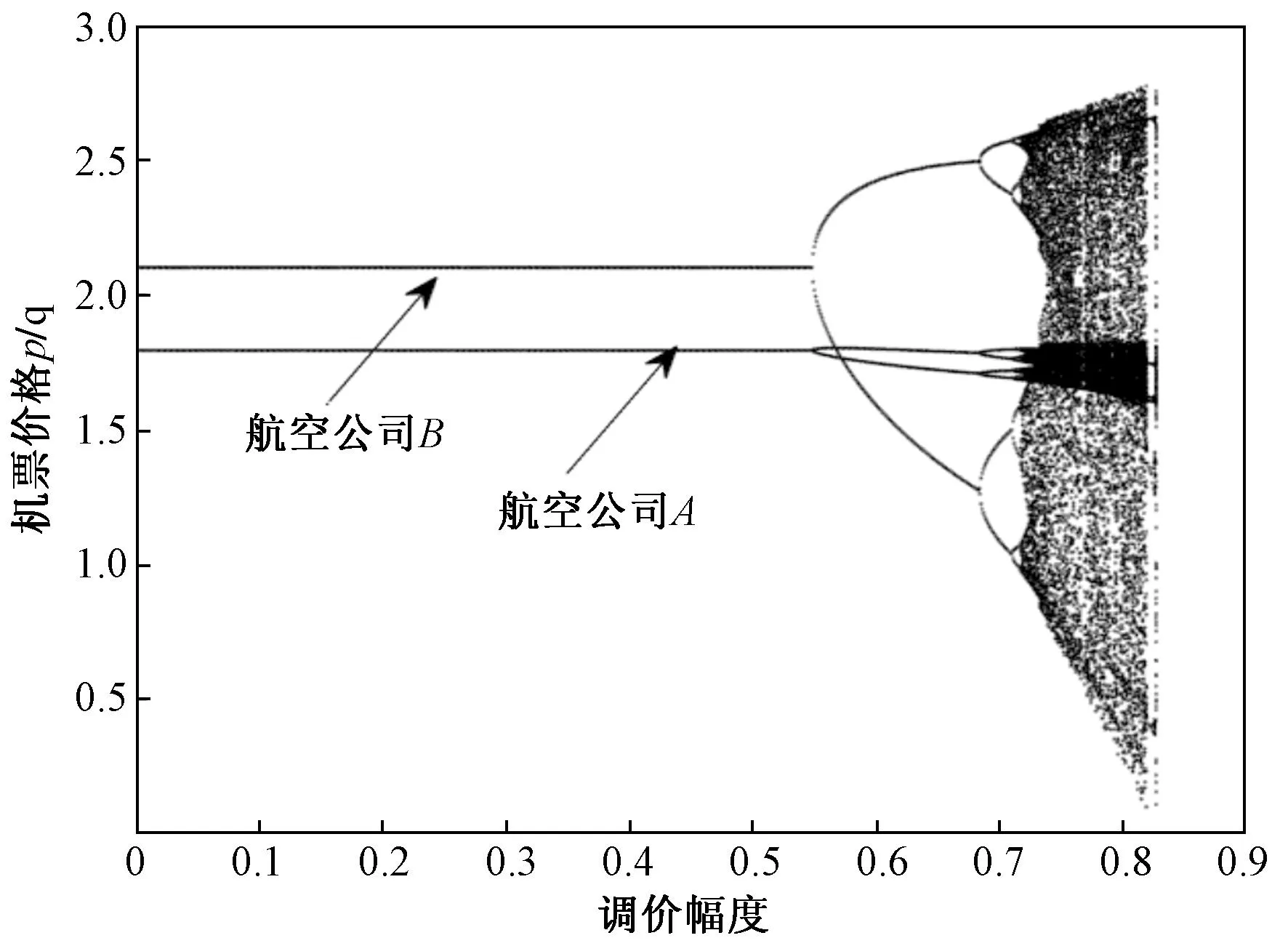
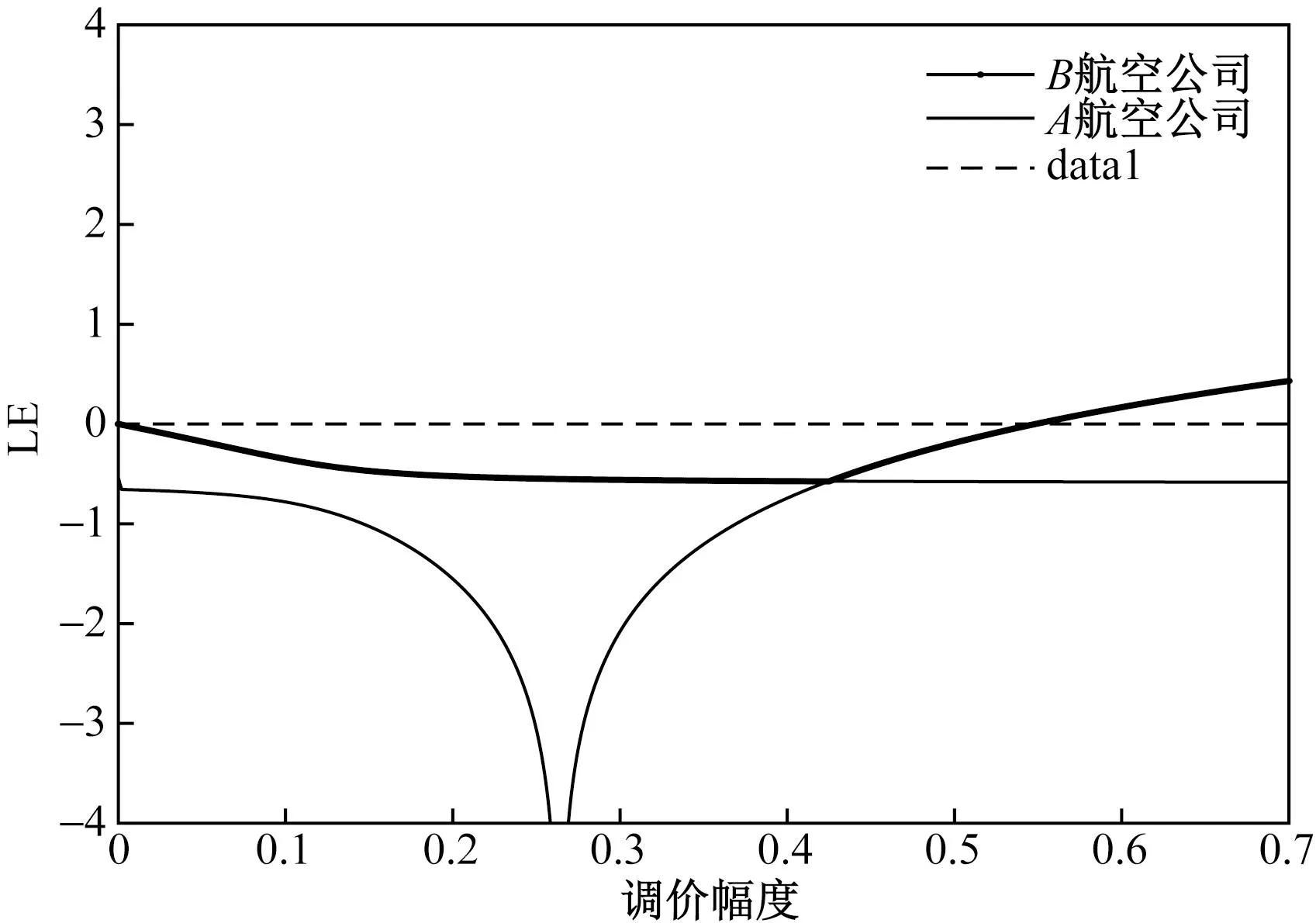
3.3 双寡头航空公司均提供附加服务
4 结论

