半球谐振子超精密修调方法研究

刘俊峰，王瑜，杜春阳，赵羽乾，戴一帆，赖涛*

半球谐振子超精密修调方法研究

刘俊峰1,2，王瑜1,2，杜春阳1,2，赵羽乾1,2，戴一帆1,2，赖涛1,2*

（1.国防科技大学 智能科学学院装备综合保障技术重点实验室，长沙 410073；2.超精密加工技术湖南省重点实验室，长沙 410073）

研究因谐振子质量缺陷而引起的频率裂解机制，进而对刚性轴位置进行质量高分辨率可控去除，提高陀螺精度。首先基于多区域配合划分法建立半球谐振子高精度有限元仿真模型，分析质量大小与位置对谐振子频差的影响规律。其次搭建谐振子振动特性检测平台，利用拍频法实现其频差值和刚性轴位置的精确辨识。最后结合仿真与辨识结果以及离子束加工方法确定谐振子超精密修调方案。优化网格划分方法后，谐振子有限元模型频差值小于0.000 1 Hz，当修调定位误差相同时，在一个范围内的质量去除比单点质量去除的修调效率更高；谐振子质量缺陷四次谐波刚性轴位置辨识精度可达0.1°，与常见的幅值法相比，其精度提高了一个数量级；通过三次点线结合方式进行质量修调后，谐振子频差值小于0.001 Hz，修调效率与精度得到了提升。提出的谐振子仿真模型、振动特性测试方法以及离子束修调工艺精度较高且可行性较强，对实现半球谐振子性能高精度检测以及高质量加工具有重要意义。

半球谐振子；频差；超精密修调；刚性轴位置；离子束加工

HRG是目前精度最高的固态振动陀螺，具有寿命长、抗冲击性强和本征抗辐射等优点[1-6]，主要由半球谐振子、施力电极和拾取电极构成。半球谐振子是其核心零件，为带有中心支撑柱的半球形薄壁壳体，直径一般为15～60 mm，壁厚一般为0.2～1.1 mm。半球壳在施力电极的作用下因挠曲变形而形成驻波，在外界旋转激励条件下驻波的哥氏效应会引起振型进动，通过拾取电极检测振型信息即可测得角速度。半球谐振子质量分布不均匀会引起频率裂解，不仅直接影响HRG角速率计算精度，还影响其镀膜以及系统的装配和激励控制，最终对陀螺稳定性、重复性、噪声、标定因素等关键指标造成影响[7]。

形位误差、材料属性不均匀等非等弹性误差是造成谐振子频率裂解的主要原因，需要通过调平工艺修正谐振子表面质量分布，补偿谐振子球壳圆周上的各向异性，使其尽可能达到理想状态[8]。Xu等[9]考虑到以小附加质量和弹簧为缺陷的圆环径向振动，引入了“等效缺陷质量”的概念，该方法适用于测量或计算模态振型接近完美的轴对称物体，可从理论上预测增减质量对频率裂解的影响。Vakhlyarsky等[10]提出了一种基于径向缺陷的简单快速的频率裂解计算方法，可将频率裂解表示为径向缺陷坐标的线性函数。在谐振子误差模型中，通常只保留密度等偏差的第4次谐波，而文献[11]指出，密度不均匀的1～3次谐波所引起的频率裂解与对应谐波成分的平方成正比，若想进一步提高调平极限，有必要辨识前3次谐波误差。哈尔滨工业大学赵洪波[12]利用解微分方程的布勃诺夫-加廖尔金法建立了包含谐振子密度不均匀1～4次谐波成分的动力学方程和密度辨识模型，并结合振动试验得到了各次谐波幅值和相位，推导了平衡谐振子密度不均匀的方法，该辨识与平衡方法有待在加工平衡过程中得到进一步验证。由于理论模型难以模拟实际的谐振子误差，目前大多研究者通过各类仿真软件分析质量缺陷对谐振子频率裂解的影响[13-15]，但当频差达到mHz级别时，网格划分带来的不对称会给频差仿真分析带来影响。

根据理论仿真与误差辨识结果，可以通过机械去重、化学腐蚀、离子束刻蚀和激光去重等手段对谐振子进行质量调平，其中机械去重方法难以满足高精度调平；化学腐蚀方法可以高效地去除熔石英材料，但可控性差，难以满足高精度要求；CO2激光加工则可能因为激光辐照的热效应而引起品质因数不均匀；超快激光对熔石英半球谐振子的点式去重修调具有独到的优势，中船集团和北京理工大学基于超快激光点式去重修调方法，将谐振子裂解频率修调至8 mHz左右，实现了0.5 mHz的修调分辨率[16]。基于离子束刻蚀的连续去重方案是国内外单位最依赖的质量调平手段，当频率裂解修调至较小量级时，对刻蚀精度要求更为苛刻，对质量可控去除分辨率的要求也越高。离子束加工可以实现原子级的材料去除，高确定性、高稳定性和非接触、无应力的加工方式使其成为谐振子修调的可靠工艺手段[17]，但有关具体离子束修调工艺的研究鲜有报道。

鉴于此，本文建立了半球谐振子高精度仿真模型，分析了质量缺陷对谐振子频率裂解的影响，搭建了谐振子振动特性检测平台，实现了谐振子频差与质量缺陷四次谐波刚性轴位置的精确辨识，并结合仿真与辨识结果以及离子束加工工艺对谐振子进行了修调试验。

1 谐振子频率裂解分析

1.1 频率裂解机制

HRG是利用科里奥利力来感知半球谐振子唇沿进动效应从而感测本体旋转的一种固体波动陀螺。理想半球谐振子在各个方向上均为轴对称结构，在模态阶数=2的振动模式下也只有一根固有刚性轴。由于实际半球谐振子存在缺陷以及材料密度不均匀、杨氏模量各向异性的情况，故谐振子中出现了2个沿和方向角度间隔为45°的固有刚性轴。在2个固有刚性轴位置，谐振子的固有频率分别达到最大值1和最小值2，2个频率之间的差值为频率裂解值（频差）Δ，如图1所示。这2个轴系的固有频率存在差值，这个值就被称为频差，这个现象就被称作谐振子的频率裂解。频率裂解值的大小直接影响了HRG的精度。因此，对频率裂解进行研究，减小频率裂解值十分重要。

由于半球谐振子的主体是薄壁半球壳，比较复杂，因此直接对半球谐振子进行频率裂解分析较为困难，需对其进行简化。可以将谐振子半球壳看作是无数个半径逐渐变化的圆环的叠加，故将对半球壳的频率裂解研究转化为对圆环的振动特性分析。同时，由于实际中谐振子缺陷很小，可将半球谐振子的缺陷替换为完美圆环上的附加点质量、无质量径向弹簧和无质量周向扭转弹簧[18]。这种方法不仅简化了谐振子的频率裂解分析过程，还可以用于指导应该向环的哪个位置增减质量，从而达到指导如何减小频差的效果。

1.2 有限元仿真

有限元仿真目前是进行半球谐振子动态性能分析最常见的方法，但在选定单元对模型进行网格划分时会存在一定的网格质量不对称的现象，导致理想模型也会产生频率裂解，进而造成质量缺陷与频差关系的仿真结果产生一定偏差，不利于指导mHz级别的频差修调。为提高仿真模型精度，采用多区法配合谐振子划分将壳体等分为16份，分别控制每部分的网格划分，最后单独处理上下2个平面的网格。划分好网格后，根据谐振子实际工况施加边界条件进行模态分析。基于多区法划分的谐振子有限元仿真模型及其第四、五阶振型如图2所示。可知，优化网格划分方法后，理想谐振子频差已达到0.09 mHz。不同网格划分方法下理想谐振子的频差如表1所示。可知，与其他网格划分方法相比，采用多区法划分的模型频差实现了数量级的提升，为后续仿真缺陷质量对谐振子频差影响奠定了基础。

质量缺陷四次谐波是影响半球谐振子频率裂解的主导因素，故通常通过对质量缺陷四次谐波分量进行修调来达到调频的目的[10,12,14]。目前超精密磨抛后的谐振子初始频差在0.1 Hz左右，对应的质量缺陷四次谐波相对幅值很小，为方便修调，基本采取等效集中质量的方法[16]。在模型上附加无体积的点质量，保证在附加质量的同时不带来刚度变化的影响。在谐振子边缘施加4个质点，每两个质点间隔90°，质点在经线上的位置分别为唇口、离唇口1 mm和2 mm处，每次仿真的点质量大小分别为0.5、1、1.5、2、2.5、3 μg。如图3所示，随着质量的增大，谐振子频率裂解值也随之增大，并且在相同质量增量的情况下，质点越靠近谐振子边缘，频率裂解值也越大。如果将点质量的变化看作是谐振子的点式修调，随着质量的下降，可以看出谐振子四波腹模态下高频频率变化很小，频率裂解降低主要是由于低频频率增大，接近高频频率。这与理论分析结果[7,9]相符，但是数值有一定差距，这主要是因为理论推导时使用了环模型来替代半球壳模型，且在理论推导结束仿真时忽略了弹簧对环的影响。

图2 半球谐振子有限元仿真模型及模态分析

表1 不同网格划分方法下半球谐振子的频率差值

Tab.1 Frequency difference values of hemispherical harmonic resonators with different grid division methods Hz

在半球谐振子的实际修调过程中，修调定位误差和去除函数波动会影响去除位置的精度和去除质量的多少，对修调结果产生一定的影响。为了防止修调实验中产生修调定位误差过大的情况，采取在刚性轴（即点质量去除位置）左右对称直线位置去除同等质量，以此来抑制因修调定位误差而导致修调效率过低的问题。在附加额外质点处左右各选取2点，连同额外质点共5点，相隔90°共20点进行质量去除，每点去除0.2 μg，使去除总质量等于额外总质量。在5点去除的情况下考虑定位误差，分别偏置5.6°和11.2°，仿真结果如表2所示，随着修调定位误差的增大，修调效率降低。当偏置角度为0°、5.6°、11.2°时，降比分别为83.4%、78%、52%。与单点去除相比，当修调定位误差相同时，在一定范围内去除质量的修调效率明显更高。考虑到实际中的半球谐振子固有刚性轴位置是由马克笔标出的，笔痕具有一定宽度，定位误差不可避免，而点式修调与直线范围修调的实际加工时间相近，故实际修调中先采用直线质量去除方法，待频差调至0.01 Hz以内时再采取点式质量去除方法。

图3 四次谐波等效集中质量对频率裂解的影响

表2 修调定位误差对频差的影响

Tab.2 Effect of positioning error of modification and levelling on frequency difference Hz

2 谐振子质量缺陷四次谐波辨识

2.1 半球谐振子振动系统测试平台

在实际修调过程中，还需辨识出半球谐振子频差以及质量缺陷四次谐波的刚性轴位置[19-20]。结合仿真结果确定修调质量与位置，因此搭建谐振子振动特性高精度测试系统来确定谐振子频差与刚性轴位置至关重要。

测量谐振子振动特性通常需要装夹、激励、测振传感器、真空环境等几个模块[21-23]。为获取较大的振幅，采用压电陶瓷片激励；采用三角爪盘或弹性夹簧装夹谐振子，将其置于转台上以方便获取不同方位角的振动信号；测振传感器采用Polytec公司的Vibroflex激光多普勒测振仪；定制真空腔以消除谐振子振动测试时空气阻尼的影响，测试环境的真空度不低于1×10−3Pa。搭建的振动测试系统如图4所示。

由于在振动测试过程中真空泵一直在运转，测振系统同时配备了主动隔震系统。图5为测振模块置于主动隔震平台和普通气浮平台上的振动信号。可知，主动隔震平台可以有效抑制振源的影响，提高振动信号精度。

2.2 频差与四次谐波刚性轴位置辨识

2.2.1 半球谐振子频差测试

当谐振子受激励自由振动时，如果激励方向不沿着刚性轴方向，谐振子的驻波就会向固有刚性轴位置移动。根据半球谐振子四波腹模态振动方程[12]，谐振子唇口位置沿、方向的振动如式（1）所示。

图4 半球谐振子振动测试平台

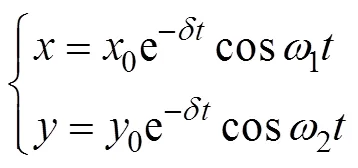
式中：0、0分别为、方向上的最大振幅；为时间；为单位冲击函数。

将2根固有刚性轴方向的振动合成，考虑到驻波与法向轴之间的夹角0，得到方位角处的振动方程如式（2）所示。

图5 主动隔振台与气浮隔振台效果对比

式中：0为2个方向上的合成幅值。

式（2）为2个简谐波的叠加，当2个振幅和频率相近的简谐波叠加时，合成波的振幅将会以为周期发生变化，产生类似于节拍的形式，这种现象被称为拍频。由于二者频率相近且不相等，波之间会产生相位差，当相位相同时，二者振幅叠加，表现为2倍振幅；当相位相反时，二者振幅抵消，表现为没有振动。根据拍频产生的原理，拍频的周期仅与2个简谐波的频率有关，则合成波的周期如式（3）所示。

某个谐振子的振动信号如图6所示，图6中有完整的14个拍频周期。利用拍频法测量频率裂解最大的误差来源于读数不准确，为尽量减小这类误差，通过读取所有周期的总时长以将一次读数误差平均到14份拍频周期中去，再多次读取总时长取平均值，这样可以将误差降到最小，最后得到谐振子的频率裂解值为0.152 1 Hz。

图6 半球谐振子拍频振动信号

谐振子传统测试方法有幅频响应法（AFR）和快速傅里叶变换法（FFT）。AFR法是通过小范围、短步长、长时间的扫频来观察不同频段幅度大小，从而获得频率裂解值。但是在实际测试中，如果谐振子长时间振动，固有频率会因为温度上升而发生漂移，小幅增大，如实测激励14.5 min，谐振子固有频率增大了0.1 Hz。对于毫赫兹级别的测试，在观测到第一个峰值后，第二个峰值会少许后移，造成测试结果不准确。FFT法是对时域图做傅里叶变换转化到频域，观测频谱图上的2个峰值来获得频率裂解值。FFT法峰值曲线会出现不光滑现象，受到数据量的限制，数据增加后也会由于频率漂移导致数据不准确。因此，拍频法适用范围广、分辨率高、误差小、方法简单，适合高品质半球谐振子频差的测量。

2.2.2 质量缺陷四次谐波刚性轴位置辨识

质量缺陷四次谐波刚性轴位置是半球谐振子质量修调位置，如何准确辨识至关重要。目前通常采用幅值观测法来识别刚性轴位置[19]，但这种方法对谐振子品质因数和测量环境要求高，且辨识精度只能达到1°左右。

当测振位置不在固有刚性轴上时，收集到的信号为由2个频率相近的振动信号叠加而成的拍频信号；当测振位置在固有刚性轴上时，收集到的信号为均匀自由衰减的振动信号。基于这个规律，以5°为单次旋转角度旋转转台，同时观察波形变化情况。当观察到拍频逐渐消失时，调整单次旋转角度为1°，继续观察波形变化情况，直到拍频几乎不见，在刚性轴位置附近时，调整单次旋转角度为0.1°来回测量，找到拍频完全消失、振动波形衰减最均匀处即为刚性轴位置。拍频法测得的刚性轴位置的振动信号结果如图7所示。在距离半球谐振子刚性轴位置0.3°时，拍频现象已经十分微弱，继续微调角度，振动将均匀衰减，此时即为固有刚性轴位置，当角度调整过度时，拍频再次出现。由此可以证明利用拍频法测量半球谐振子固有刚性轴位置可行，且辨识精度可达到0.1°，为实现半球谐振子超精密修调奠定了基础。

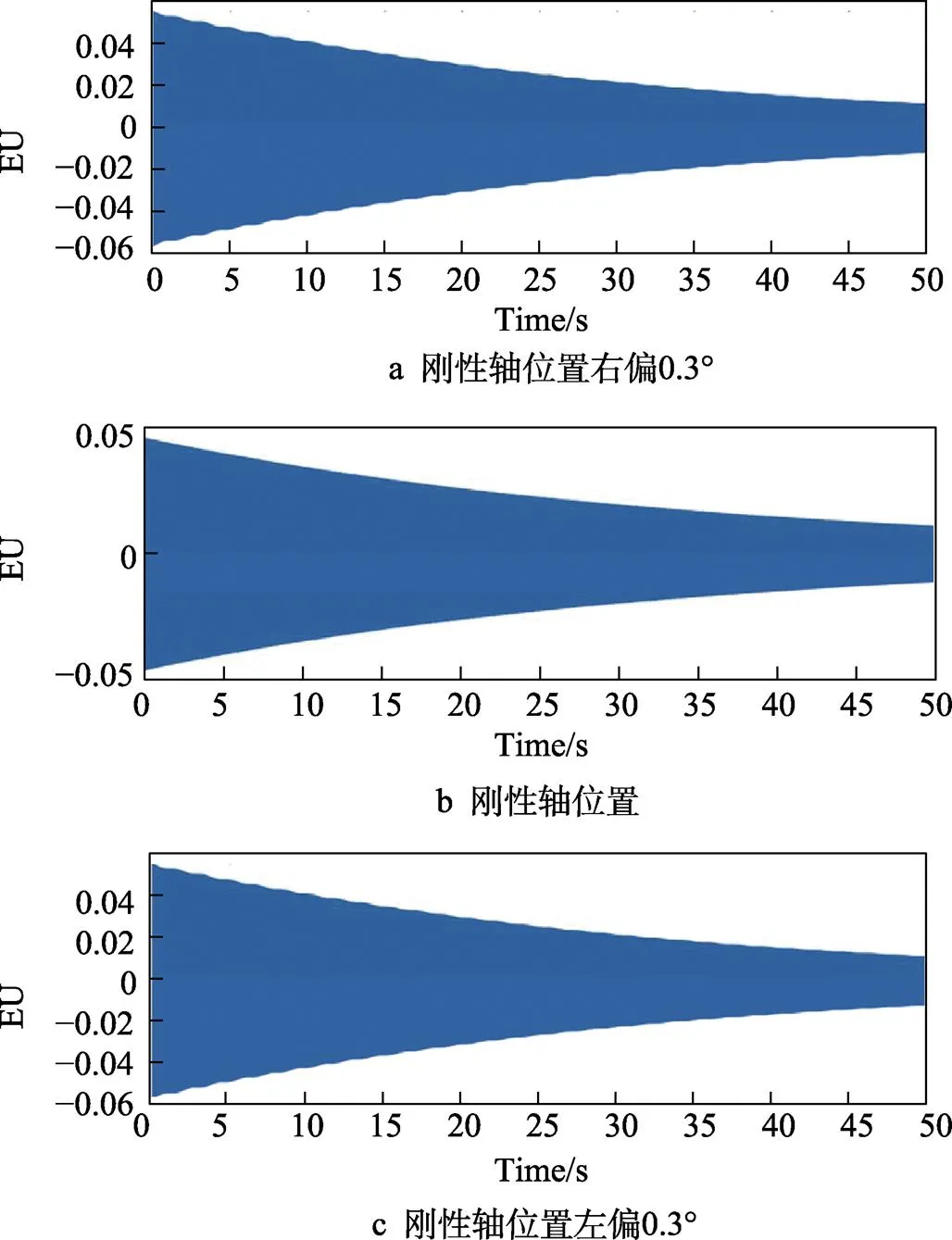
图7 拍频法测半球谐振子刚性轴位置

3 基于离子束的半球谐振子修调方法

3.1 去除函数确定

离子束加工的原理是通过离子源形成一定浓度的等离子体，再通过聚焦离子光学系统引出带有一定能量的离子束轰击工件表面，通过与工件表面原子的碰撞将动能传递给原子，当动能大于原子的束缚能时，原子将会脱离工件表面，从而完成材料去除，这是目前加工精度最高的加工方式。离子束的束流密度通常为回转对称的高斯函数，其刻蚀速率与入射离子能量、溅射离子数量、离子入射深度、入射角度和散射宽度有关[24]。为获取离子束对谐振子材料的去除函数，对熔石英材料开展去除函数实验，实验机床选用自主研发的KDIBF650离子束机床，具体参数如下：直径30 mm的栅网，直径2 mm的光阑，靶距为10 mm，离子束入射能量为800 eV，束流大小为60 mA。对直径50 mm的熔石英平板进行加工，在间隔20 mm的4个位置进行离子束轰击，每点去除2 min，最终通过面形测量获得去除效率为0.155×10−3mm3/min。

3.2 离子束修调实验

利用拍频法测量待修调的谐振子频差后，根据图3仿真结果确定需要去除的质量缺陷四次谐波分量值，再结合图7所示的拍频法确定质量去除位置，完成谐振子超精密修调。由上文仿真分析结果可知，当半球谐振子频率裂解值较大时，为了提高修调效率，降低修调定位误差，选取离子束直线去除调平的方法对半球谐振子进行修调，同时避免点式修调方法因初始频差较大、加工时间较长而带来加工出小坑的问题。在修调结果达到mHz级别的情况下，当离子束在很短的时间内扫过一条直线时，会出现能量过小、去除函数不稳定的情况，此时再采用离子束点式修调的方法进行加工。由于去除函数具有一定的宽度，为了保证去除函数的完整性，选择在谐振子边缘经线方向2 mm处进行加工，加工形状为以低频轴位置为中心的4 mm直线轨迹，加工4个位置，每个位置覆盖角度为22.92°。当每次加工完一个位置后，移开离子束，待电机旋转到下一个位置时移回离子束继续加工。离子束参数设置与获得去除函数时的一致。

由于谐振子是半球形，因此离子束并不是绝对垂直照射在表面上的，具有小角度偏差入射的特点。在接近垂直入射时，角度偏差对去除速率的影响很小[25]，故认为离子束去除效率与去除函数一致。半球谐振子离子束修调实验图如图8所示。

图8 半球谐振子离子束修调实验

选取自主磨抛的熔石英半球谐振子为修调对象，谐振子口径为20 mm，初始频差为0.081 1 Hz，品质因数为1 510万。根据谐振子修调前的状态，第1次修调采取直线去除方式，从第2次开始采取点式去除方式，修调过程与结果如表3所示。可知，经过3次修调后，谐振子频差达到0.000 79 Hz（如图9所示），验证了本文提出的半球谐振子修调方法的准确性与高效性。

表3 半球谐振子修调实验过程与结果

Tab.3 Process and result of modification and levelling test of hemispherical harmonic resonator

图9 修调后谐振子频差

4 结论

提出了半球谐振子超精密修调方法并进行了离子束修调实验，具体结论如下：

1）提出的半球谐振子高精度有限元仿真模型将因网格单元分布不对称而带来的频差减小至0.000 09 Hz，基于该模型分析了修调质量与位置对谐振子频差的影响。

2）搭建了半球谐振子振动测试系统，在采用提出的振动特性方法后，测量精度得到了提升，其中质量缺陷四次谐波刚性轴位置辨识精度可达0.1°，为下一步修调提供了精准的位置。

3）基于仿真与辨识结果，结合离子束加工工艺进行半球谐振子修调实验，经过3次修调后，谐振子频差达到0.000 79 Hz。

[1] MATTHEWS A, RYBAK F J. Comparison of Hemispherical Resonator Gyro and Optical Gyros[J]. Aerospace and Electronic Systems Magazine, 1992, 7(5): 40-46.

[2] LYNCH D, MATTHEWS A, VARTY G T. Innovative Mechanizations to Optimize Inertial Sensors for High or Low Rate Operations[C]// Symposium Gyro Technology 1997, Stuttgart, Germany, 1997.

[3] BARBOUR N M. Inertial Navlgahon Sensors[R]. Charles Stark Draper Lab Inc Cambridge Ma, 2010.

[4] KORKISHKO Y N, FEDOROV V A, PRILUTSKIY V E, et al. Highest Bias Stability Fiber-optic Gyroscope SRS-5000[C]// Dong Inertial Sensors and Systems, Karlsruhe: IEEE, 2017: 1-23.

[5] ANTHONY M. The Operation and Mechanization of the Hemispherical Resonator Gyroscope[C]// IEEE/ION Position, Location and Navigation Symposium, Monterey CA, 2018: 7-14.

[6] 帅鹏, 魏学宝, 邓亮. 半球谐振陀螺发展综述[J]. 导航定位与授时, 2018, 5(6): 17-24.

SHUAI P, WEI X B, DENG L. A Survey of Hemispherical Resonator Gyro[J]. Navigation Positioning and Timing, 2018, 5(6): 17-24.

[7] 徐志强, 刘建梅, 王振, 等. 石英半球谐振子精密加工技术探讨[J]. 导航与控制, 2019, 18(2): 69-76.

XU Z Q, LIU J M, WANG Z, et al. Discussion on Precision Machining Technology of Quartz Hemispherical Harmonic Oscillator[J]. Navigation and Control, 2019, 18(2): 69-76.

[8] FOX C H J. A Simple Theory for the Analysis and Correction of Frequency Splitting in Slightly Imperfect Rings[J]. Journal of Sound and Vibration, 1990, 142(2): 227-243.

[9] XU Z Y, YI G X. Acceleration Drift Mechanism Analysis and Compensation for Hemispherical Resonant Gyro Based on Dynamics[J]. Microsystem Technologies-micro-and Nanosystems-information Storage and Processing Systems, 2016, 25(9): 3425-3435.

[10] VAKHLYARSKY D S S, SOROKIN F S S, GOUSKOV A S S, et al. Approximation Method for Frequency Split Calculation of Coriolis Vibrating Gyroscope Resonator[J]. Journal of Sound & Vibration, 2022.

[11] 周小刚, 汪立新, 佘嫱, 等. 半球谐振陀螺加速度影响分析与实验研究[J]. 仪器仪表学报, 2008, 29(4): 237-241.

ZHOU X G, WANG L X, SHE Q, et al. Acceleration Consequence Analysis of HRG and Experiment Research[J]. Chinese Journal of Scientific Instrument, 2008, 29(4): 237-241.

[12] 赵洪波. 半球谐振子频率裂解分析与陀螺仪误差抑制方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.

ZHAO H B. On Frequency Split Analysis for Hemispherical Resonator and Error Restraint Method for the Hemispherical Resonator Gyroscope[D]. Harbin: Harbin Institute of Technology, 2013.

[13] 郑超, 张林, 肖茵静. 半球谐振陀螺谐波缺陷振动特性有限元分析[J]. 导航与控制, 2022, 21(2): 83-90.

ZHENG C, ZHANG L, XIAO Y J. Finite Element Analysis of Harmonic Defect Vibration Characteristics of Hemispherical Resonator Gyroscope[J]. Navigation and Control, 2022, 21(2): 83-90.

[14] 王鹏, 曲天良, 刘天怡, 等. 半球谐振子质量不平衡对振动特性的影响研究[J]. 仪器仪表学报, 2023, 44(3): 244-252.

WANG P, QU T L, LIU T Y, et al. Influence of Mass Unbalance of Hemispherical Resonator on Vibration Performance[J]. Chinese Journal of Scientific Instrument, 2023, 44(3): 244-252.

[15] 陈一铭. 半球谐振陀螺谐振子检测及调平技术研究[D]. 北京: 中国航天科工集团第二研究院, 2022.

CHEN Y M. Detection and Mass Balance Technology of Resonator for HRG[D]. Beijing: The Second Academy of CASIC, 2022.

[16] 赵小明, 于得川, 姜澜, 等. 基于超快激光技术的半球谐振陀螺点式修调方法[J]. 中国惯性技术学报, 2019, 27(6): 56-60.

ZHAO X M, YU D C, JIANG L, et al. Point-trimming Method of Hemispherical Resonator Gyroscope Based on Ultrafast Laser Technology[J]. Journal of Chinese Inertial Technology, 2019, 27(6): 56-60.

[17] HUO Y, WEI Z N, REN S Q, et al. High Precision Mass Balancing Method for the Fourth Harmonic Mass Defect of Fused Quartz Hemispherical Resonator Based on Ion Beam Etching Process[J]. IEEE Transaction on Industrial Electronics, 2022, 70(9): 9601-9613.

[18] HOSSEINI P M, TATAR E. Analysis of Quadrature and Frequency Split in a Mems Vibrating Ring Gyroscope with Structural Imperfections[C]// 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 2021: 112-119.

[19] 李巍, 金鑫, 任顺清. 半球谐振陀螺仪频率裂解及固有刚性轴的测试方法[J]. 传感技术学报, 2016, 29(3): 338-342.

LI W, JIN X, REN S Q. Measurement of Frequency Splitting and Inherent Rigidity Shaft of Hemispherical Resonator Gyro[J]. Chinese Journal of Sensors and Actuators, 2016, 29(3): 338-342.

[20] HE C H, WANG Y P, HUANG Q W, et al. Research on the Packaging Reliability and Degradation Models of Quality Factors for a High Vacuum Sealed Mems Gyroscope[C]// 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 2017.

[21] 李绍良, 杨浩, 夏语, 等. 基于幅频响应特性的半球谐振子频率裂解与固有刚度轴方位角测定方法[J]. 飞控与探测, 2020, 3(1): 69-74.

LI S L, YANG H, XIA Y, et al. Measurement Method of Hemispherical Resonator Frequency Splitting and Normal-mode Axis Azimuth Based on Amplitude Frequency Response Characteristics[J]. Flight Control & Detection, 2020, 3(1): 69-74.

[22] LI S L, YANG H, ZHAO W, et al. Research on the Time-Domain Measurement Method of Low-Frequency Splitting for Hemispherical Resonator[J]. Journal of Sensors, 2021, 2021(3): 1-10.

[23] SUP C. Internal Friction in Solids II. General Theory of Thermoelastic Internal Friction[J]. Physical Review, 1938(1): 90-99.

[24] 焦长君, 解旭辉, 李圣怡, 等. 光学镜面离子束加工的材料去除效率[J]. 光学精密工程, 2008, 16(8): 1343-1348.

JIAO C J, XIE X H, LI S Y, et al. Material Removal Efficiency in Ion Beam Figuring for Optical Component[J]. Optics and Precision Engineering, 2008, 16(8): 1343-1348.

Method of Ultra-precision Modification and Levelling of Hemispherical Harmonic Resonators

LIU Junfeng1,2, WANG Yu1,2, DU Chunyang1,2, ZHAO Yuqian1,2, DAI Yifan1,2, LAI Tao1,2*

(1. Laboratory of Science and Technology on Integrated Logistics Support , College of Intelligence Science and Technology, National University of Defense Technology, Changsha 410073, China; 2. Hunan Key Laboratory of Ultra-Precision Machining Technology, Changsha 410073, China)

The work aims to study the frequency splitting mechanism caused by quality defects of the resonator and conduct high-resolution controllable quality removal on rigid axis position to improve the accuracy of hemispherical resonant gyroscope (HRG). Firstly, a high-precision finite element simulation model of a hemispherical harmonic resonator was established based on the method of multi region coordination division, and the effect of mass size and position on the frequency difference of the harmonic resonator was analyzed. Secondly, a platform for measuring the vibration characteristics of the harmonic resonator was establish, and the frequency difference value and the position of rigid axis were accurately identified based on the beat frequency method. Finally, the ultra-precision modification and levelling scheme of the harmonic resonator was determined by combining simulation and identification results with ion beam processing methods. After optimizing the grid division method, the frequency difference value of the finite element model of the harmonic resonator was less than 0.000 1 Hz. Compared with single point removal, when the positioning error was the same, the modification efficiency of quality removal within a range was higher than that of single point quality removal. The identification accuracy of the fourth harmonic rigid axis position of the quality defect of the harmonic resonator was able to reach 0.1°, which was an order of magnitude higher than the common amplitude method. The frequency difference value of the harmonic resonator after three rounds of modification and levelling through the combination of dots and lines was less than 0.001 Hz, which improved the efficiency and accuracy of modification and levelling. The proposed harmonic resonator simulation model, vibration characteristic testing method, and ion beam tuning process have high accuracy and strong feasibility, which is of great significance for achieving high-precision detection and high-performance processing of hemispherical harmonic resonator.

hemispherical harmonic resonator; frequency difference; ultra-precision modification and levelling; position of rigid axis; ion beam processing

10.3969/j.issn.1674-6457.2024.01.018

TH162

A

1674-6457(2024)01-0158-09

2023-09-22

2023-09-22

国家自然科学基金（52375473，51991372）；国防科技重点实验室基金（KT0406052303）

The National Natural Science Foundation of China (52375473, 51991372); National Defense Science and Technology Key Laboratory Fund (KT0406052303)

刘俊峰, 王瑜, 杜春阳, 等. 半球谐振子超精密修调方法研究[J]. 精密成形工程, 2024, 16(1): 158-166.

LIU Junfeng, WANG Yu, DU Chunyang, et al. Method of Ultra-precision Modification and Levelling of Hemispherical Harmonic Resonators[J]. Journal of Netshape Forming Engineering, 2024, 16(1): 158-166.

（Corresponding author）