汽车用先进高强钢本构模型与韧性断裂模型研究进展

巢成新，于强,2*，李秋

汽车用先进高强钢本构模型与韧性断裂模型研究进展

巢成新1，于强1,2*，李秋1

（1.天津职业技术师范大学 机械工程学院，天津 300222；2.西安交通大学 机械工程学院 机械制造系统工程国家重点实验室，西安 710049）

轻量化是当前汽车行业全产业链共同面对的课题，提高先进高强钢使用比例是实现汽车轻量化的有效手段。对先进高强钢本构模型与韧性断裂模型的充分研究有助于提高先进高强钢开裂分析和预测的准确性，从而推动先进高强钢工程的应用进程。目前，在先进高强钢的研究过程中，学者们通常通过多种应变强化模型的线性组合，或结合微观结构与宏观力学行为进行多尺度分析来建立本构模型；通过多种应力状态下的准静态拉伸实验以及使用仿真与实验混合的方法来标定韧性断裂模型的参数。以第三代先进高强钢中的淬火配分（QP）钢为重点讨论对象，介绍了制备工艺与材料特性及其相关研究进展，并介绍了QP钢本构模型的研究现状、新近发展的非耦合韧性断裂模型以及考虑了应力三轴度和罗德角参数影响的韧性断裂模型在先进高强钢上的应用现状，最后指出了先进高强钢本构模型和韧性断裂模型未来的研究方向。

轻量化；先进高强钢；冲压成形；本构模型；韧性断裂模型

汽车轻量化不仅能降低汽车油耗、实现节能减排，还有助于提升车辆的可回收性和驾驶性能，是汽车制造业的重要发展方向[1]。采用包括铝合金、镁合金、碳纤维等在内的轻质材料替代钢材和使用先进高强钢（Advanced High Strength Steels，AHSS）替代低强度钢，是实现汽车轻量化的2种有效手段[2-3]。然而，镁铝合金、碳纤维等轻质材料在生产过程中排放的CO2是钢的5～20倍，且加工与回收成本都远高于钢材[4]。因此，从全生命周期角度出发，钢铁材料在汽车轻量化、节能减排、成本控制等方面更具发展潜力。

根据世界钢铁协会下属的汽车用钢分会——世界汽车用钢联盟给出的定义，先进高强钢包括所有的马氏体钢和多相钢，抗拉强度至少为440 MPa[5]。先进高强钢主要应用于汽车结构件、安全件及加强件中，如A/B/C柱、车门防撞梁、保险杠等，工业上通常采用冲压成形的方法进行先进高强钢零件的制造。先进高强钢具备复杂的微观结构，可通过在生产过程中调控化学成分和加工条件获得相应的显微组织，进而促进材料形成所需性能[6]。然而，这种混合的微观结构也容易使结构件成形过程中的回弹、起皱和破裂等行为难以控制[7]，且随着先进高强钢强度等级的提升，在成形过程中容易出现边角部开裂的现象，在圆角处还会出现一种无法通过成形极限曲线预测的剪切断裂，这些问题都影响着先进高强钢在汽车制造上的大规模应用。在板料成形领域多采用韧性断裂模型进行开裂预测，选择一个能够准确描述材料塑性和断裂行为的本构模型则是进行开裂预测分析的前提[8]。本文以第三代先进高强钢的典型代表——淬火配分（Quenching and Partitioning，QP）钢为重点讨论对象，介绍了制备工艺与材料特性及其相关研究进展、QP钢本构模型的研究进展以及新近发展的非耦合韧性断裂模型，并综述了断裂模型在先进高强钢上的应用现状。

1 QP钢的制备工艺与材料特性

先进高强钢（AHSS）发展到现在已至第三代。双相钢（Dual Phase，DP）是第一代AHSS的代表钢种，因具有成本低、成形性能好、易于加工等优点而在工程上广泛应用。然而，DP钢的成形性能会随着抗拉强度的提升而降低，且DP钢中的铁素体与马氏体之间的性能差异过大，在冲压过程中容易出现应力集中进而导致开裂现象[9]。孪晶诱导塑性钢（Twinning Induced Plasticity，TWIP）属于第二代AHSS，其合金化程度较高，力学性能优异，但制备工艺复杂，成本较高，因此在工业生产中不具备优势[10]。第三代先进高强钢填补了第一代和第二代先进高强钢之间的性能空缺，如图1所示。QP钢和中锰钢是第三代AHSS的代表钢种，其中中锰钢属于尚在开发中的钢种，而QP钢工业化生产工艺较为成熟，质量稳定可控，与第一代AHSS相比具备更好的强度和塑性配合，并且没有第二代AHSS制造成本高昂的缺点，同时其耐冲击性能与成形性能也相对较好，在商业应用中具有广阔的应用前景[11]。

QP钢的特点是在制备过程中采用了一种新型热处理工艺——淬火配分工艺，这种工艺由Spee于2003年提出，该工艺通过调控金相组织的方法，在只牺牲小部分强度的情况下，使钢的塑性获得极大提升。淬火配分工艺流程如图2所示[12]。先将钢加热到发生奥氏体化的转变温度（c3）之上，保持某一温度值一段时间，待材料内部晶体结构完全转化为奥氏体后，对钢材进行淬火处理，使材料温度迅速下降到马氏体转变温度（sf），获得马氏体和部分亚稳奥氏体，在淬火温度下保温可以使碳原子从马氏体向亚稳奥氏体富集，迁移到亚稳奥氏体中的碳原子会提高残余奥氏体的稳定性，抑制它向马氏体转变；在淬火保温后将配分温度适当提升，可以加速碳原子向残余奥氏体迁移，同时保持马氏体体积分数不变，配分完成后再进行二次淬火可以获得稳定的残余奥氏体。

QP钢的最大特性是具有应变诱发相变（Transformation Induced Plastics，TRIP）效应，即在冲压过程中，残余奥氏体在应力的作用下发生TRIP效应，使软相的奥氏体转变为体积更大的硬相马氏体，从而提高钢的强度与韧性[13-14]。在QP钢变形的过程中，应力状态、温度和应变率等因素会对残余奥氏体向马氏体转变的规律产生显著影响。在应力状态对QP钢的TRIP效应影响方面，冯怡爽等[15]和Wang等[16]对QP980钢在不同变形模式下的力学性能和金相含量进行了测试，发现应变路径会对QP980钢的应变诱发马氏体相变行为产生显著影响，同样在施加线性载荷的情况下，马氏体相变的速度表现出明显的差异，从快到慢的顺序为：等双拉、平面应变、单向拉伸、单向压缩和纯剪切。在温度对TRIP效应影响规律方面，不少学者已达成共识：根据马氏体相变理论[17]，相变的化学驱动力会随着温度的升高而降低，在外界机械驱动力相同的情况下，温度升高则会抑制马氏体的相变[18]。宝钢股份有限公司的Feng等[19]在−60～60 ℃温度范围内对QP钢的相变规律进行了实验研究，发现QP钢的相变行为对温度的敏感性较强。然而在该研究中，−60～60 ℃的温度区间并不能覆盖零件冲压过程中实际工况的温度范围。在应变率对QP钢TRIP效应影响研究方面，Zou等[20]通过间断性的单向拉伸实验和X射线衍射测量发现，当应变速率低于0.1 s−1（0.000 2～0.1 s−1）时，塑性变形产生的热量减缓了马氏体相变；当应变速率超过0.1 s−1（0.1～175 s−1）时，马氏体形核点位增多，应变速率的增大加速了马氏体相变。Ding等[21]在5种应变率下对QP980钢板进行了单轴拉伸实验，研究了其颈缩过程以及应变率对QP钢颈缩行为的影响。结果表明，在研究范围内，应变率对分散性失稳应变和集中性失稳应变都有影响，随着应变率的增大，2种应变都减小，从而导致材料的成形性能降低。侯玉栋等[22]通过5 000、10 000、15 000 s−1应变速率下的高速冲击实验发现，经高速冲击后，QP980钢板的微观组织更加细小且呈现板条化，先进高强钢所能承受的应力随应变速率的增大而增大。也有学者针对残余奥氏体含量对QP钢力学性能的影响开展了研究，Xia等[23]通过实验研究了合金化元素和微观组织成分对3种QP钢成形性能的影响，研究表明，QP钢单轴拉伸的伸长率与其成形性并不一定相关，具备最高残余奥氏体体积分数且拉伸延展性最强的QP钢表现出的成形性能却很低。邹丹青[24]针对QP钢的应变诱发相变行为进行了一系列研究，并建立了QP980钢应变诱发相变多因素耦合的动力学模型，研究发现，应变诱发相变现象对材料的应变硬化和塑性都产生了显著影响。

图1 先进高强度钢的伸长率与抗拉强度关系[5]

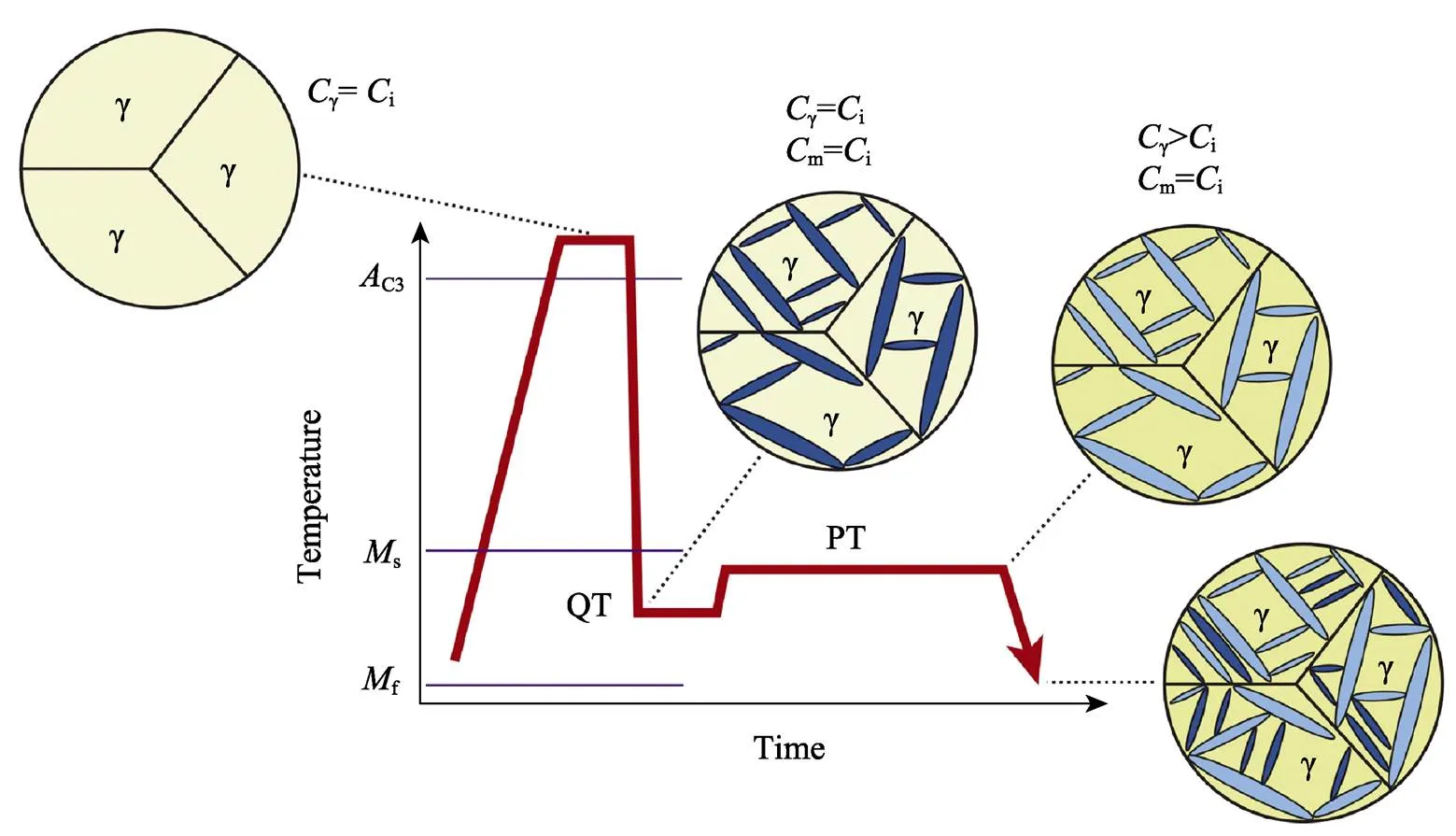
图2 QP钢二次淬火和配分热处理工艺流程[12]

通过淬火配分热处理工艺获得的QP钢金相组织保留了大量稳定的残余奥氏体，为后续钢材料变形过程中发生TRIP效应做了组织成分上的准备。在QP钢的相变过程中，残余奥氏体向马氏体的转变会引入额外的应变硬化，从而使材料呈现出独特的应力-应变响应行为，充分认识QP钢的这种特殊应力-应变响应，将有助于促进QP钢的工程应用。

2 QP钢材料本构模型研究现状

材料的本构模型是用来描述应力-应变关系以及其他材料力学性能的数学表达式，是进行有限元仿真模拟和冲压成形预测的基础。目前建立的材料本构模型主要分为2类：基于细观力学的本构模型；基于宏观经验性的唯象本构模型。

2.1 基于细观力学的本构模型

QP钢由铁素体、马氏体和奥氏体3种金相构成，QP钢碳配分前后的SEM显微照片如图3所示，其中MA、a、d分别表示马氏体、奥氏体和铁素体。可知，QP钢是一种典型的多相钢[25-26]。起初是在研究TRIP钢时开始建立基于细观力学的本构模型的。在建立多相材料的本构模型时，需要考虑材料微观组织成分和变形过程中的微观结构演变，不同金相组织体积分数的变化会引起材料应力-应变关系的变化，通常需要先使用中子衍射或X射线衍射等方法测得各个组成相独立的应力-应变关系，考虑变形过程中材料相体积分数的变化，然后再依据一定的混合法则获得材料整体的本构模型[27-28]。

丁磊等[29]采用XRD对不同应变下的QP980钢样品进行了扫描，根据铁素体/马氏体衍射峰和残余奥氏体衍射峰的面积比获得了奥氏体的体积分数，然后建立了QP980钢的相变动力学方程，采用中间混合法则建立了考虑TRIP效应的QP980钢多相本构模型。张文超[30]在等应力假设下，根据多相材料细观力学理论建立了QP980钢的细观力学模型，分析了相变与应变变化关系下各组成相的弹塑性变形，推导出了考虑了相变效应的QP980钢的动态本构方程。Arlazarov等[31]在配分温度和时间不同的淬火配分过程中获得了QP钢样品，研究了其显微组织和力学性能的演变情况，并根据获得的实验数据，提出了QP钢应力-应变曲线的预测模型，且该模型能够准确预测不同相比例的QP钢的应力-应变曲线。Connolly等[32]使用原位高能X射线衍射联合单轴拉伸实验表征了QP1180钢的应力和马氏体转变响应，并采用一种既考虑了热力学又考虑了应变速率的晶体塑性本构模型对能在大变形条件下表现出TRIP效应的QP钢的变形行为进行了表征，并将本构模型应用到热机械晶体塑性有限元方法中，以研究织构、相形态和温度对QP1180钢材料性能的影响，数值模拟结果表明，该方法仅能预测绝热条件、中等应变速率下的温度演化情况，而准静态变形和非绝热环境下的温度演化行为并不能被准确捕捉。

基于细观力学建立的本构模型考虑了材料宏观性能的微观本质以及微观应力-应变分配。相应地，这类模型的建立对各相应力-应变实验测量的精度要求非常高。然而，材料内各组成相对温度和应变率的敏感性存在差异，且各相的敏感性目前还无法通过实验准确获得。因此，当前模型难以同时考虑应变率强化和高温软化2种效应对材料性能的影响。

2.2 基于宏观经验性的唯象本构模型

宏观唯象本构模型能够有效预测金属塑性成形能力，通过有限元方法可实现材料塑性成形问题的求解，因此被广泛应用于实际工程中[33]。国内外科研人员提出了不同的唯象本构模型。

早期的本构模型形式较为简单，大多是基于经验或半经验的理论基础建立的，工程上多采用幂指数函数来描述金属材料硬化模型，Hollomo模型考虑了强化系数和硬化指数，是一种典型的应力值无上限的非饱和模型[34]。

图3 QP钢碳配分前（a）和碳配分后（b）的SEM显微照片[25]

Ludwik[35]在Hollomo模型的基础上引入了初始屈服强度，他认为流动应力是初始屈服强度、应变强化系数和硬化指数共同作用的结果。Swift模型则是在Hollomo模型的应变强化相中引入了初始屈服应变，且只对塑性变形阶段进行拟合[36]。Fields等[37]在本构关系中考虑了应变率对材料硬化产生的影响，使用应变率敏感系数来描述应变率对材料硬化的影响程度。

Voce模型是早期饱和外推模型的一种形式，该类模型的特点是流动应力随应变的增大逐渐收敛为定值，模型必定会经过屈服点，拟合所获得的饱和流动应力在最大抗拉强度附近[38]。然而实际的饱和流动应力数值应远超抗拉强度，许多学者为了使Voce达到饱和流动应力的速率减慢，提出了一系列的改进模型，如Voce+Voce模型[39]、Hockett-Sherby模型[40]等。此外，还存在一类称为非饱和模型的本构模型，即将饱和项与非饱和项叠加在一起，例如Voce++模型在Voce模型的基础上添加了二次方根项和线性项，使流动应力的增长速度显著提高[41]。

Johnson和Cook提出的J-C本构模型综合考虑了材料的应变硬化、应变速率强化以及高温热软化作用，在高应变率和高温条件下都非常适用，也是目前应用较为广泛的一种本构模型[42]。

Xia等[43]对标称屈服强度为340～1 200 MPa的DP、HSLA和MS钢进行了一系列拉伸实验，测定了材料的基本性能，包括弹性模量、屈服强度、抗拉强度和断裂伸长率，在Ramberg-Osgood模型的基础上，建立了一个新的两段式应力-应变本构模型，对于DP和HSLA钢，该模型的预测结果与实验结果具有良好的一致性。文中提到的各本构模型具体公式如表1所示。

在实际应用中，学者们通常采用优化材料参数的方法来准确描述材料的塑性，通过修正单一的本构方程来获取更高的拟合精度，通过比较多种本构方程，选择适用范围更广泛的模型[44]。Wang等[45]采用2种传统本构模型线性组合的方法，通过不断改变两者之间的权重系数，使最终获得的本构模型能够准确描述QP980钢材料的真实应力-应变关系。邹丹青[24]基于Mohr提出的与相变相关的流动应力-应变模型，在建立QP980钢本构模型时，将QP钢材料的应变硬化分解为位错强化和新生马氏体相变强化，并基于QP钢的相变动力学模型，考虑了相变强化、应变率强化、塑性温升软化和环境温度4个因素，最终建立了宏微观耦合的应力-应变模型。

除了以上关于QP钢本构关系建模的研究，学者们在其他种类先进高强钢本构模型研究上的经验也可以为QP钢本构模型建模方法的选择和模型的优化提供一定的借鉴。穆磊[46]综合利用Swift应变强化模型和Voce应变强化模型，改变了两者的权重系数，使DP780材料的实验载荷-位移曲线与仿真曲线贴合，如图4a所示，最终获得了可靠的塑性应变-真实应力曲线。Lou等[47]使用Swift模型模拟了DP980颈缩应变前的应力-应变关系，如图4b所示，在颈缩应变外，对应力-应变曲线进行了调制，使数值分析预测的载荷-行程曲线与实验结果接近。张赛军等[48]发现Swift和Voce硬化方程分别高估和低估了DP590在大应变下的应力，因此在研究中使用修正的Voce硬化准则（指数型Voce+Voce硬化准则）来表征DP590高强钢的硬化行为，如图4c所示。

表1 金属材料常用的本构模型

Tab.1 Commonly used constitutive models for metallic material

图4 不同文献中实验与模拟载荷-位移曲线的比较

3 非耦合韧性断裂模型研究的近期进展

数值模拟技术在板料成形领域得到了广泛的应用，在缩减产品开发周期、设计成形模具、选择材料与降低成本等方面发挥着重要的作用[49]。材料本构模型与韧性断裂模型的选用是影响数值模拟计算结果可信度的关键因素。材料韧性断裂模型发展到今天已有70余年的历史，传统非耦合型韧性断裂模型结构形式单一，参数识别只需进行少量的韧性断裂实验，且对较宽应力范围内金属材料韧性断裂行为的预测精度不佳[50]。为了更加精准地预测金属材料在三维应力空间内的韧性断裂性能，各国学者普遍开始建立考虑了应变历史、引入了应力三轴度和罗德角等参数的韧性断裂预测模型，这些新提出的非耦合韧性断裂模型涵盖了各种复杂应力状态下的材料损伤演化，并广泛应用于汽车与航空航天领域[51]。

Bai等[52]将应力三轴度、罗德角参数和等效塑性应变的加权函数引入到通常用来描述岩土材料力学性质的Mohr-Coulomb屈服准则中，获得了基于应变修正的摩尔库伦（MMC）断裂预测模型，该模型是广泛用于剪切型破坏预测的最大剪应力准则的延伸，可以有效预测板料成形过程中的剪切型断裂。研究表明，这一模型在TRIP钢钣金成形过程中的剪切破坏预测上取得了较好的应用效果。

Lou等[53]在2012年基于板料微孔洞的形成、生长和聚合的演化机制，提出了针对韧性破坏的Lou-Huh断裂准则模型，该模型能够准确预测剪切应变和平面应变等应力状态下的韧性断裂。为提高模型的预测性能，考虑了微观结构、变形温度和应变速率等因素对材料特性的影响，将材料的断裂应变定义成可变值。Lou等[54]在2017年对LouHuh模型进行了修正，使准则能够更准确地预测单轴拉伸、平面应变、双轴拉伸和剪切等各种应力状态下的断裂行为，提高了准则的灵活性与适用性。

Mu等[55]基于孔洞演化机制提出了一种新的韧性断裂模型，采用数学模型描述板料成形过程中的损伤累积，并将该模型转化为如图5所示的三维空间（罗德角参数、应力三轴度和等效塑性应变）中的韧性断裂曲面。通过MMC模型和LouHuh模型对DP780、DP590、5083-O铝合金3种材料的断裂预测进行误差对比分析，结果发现，新模型的累计误差均最小。上述模型的数学表达式如表2所示。

图5 DP780钢的韧性断裂曲面[55]

4 汽车用先进高强钢韧性断裂模型应用现状

复杂汽车零件的制造成形通常需要经历多道工序，包括拉延、扩孔、翻边等。在这些工序中，由于应力状态的多变和变形的非线性特性，成形过程非常复杂。在冲压成形过程中，先进高强钢面临着特殊的挑战，如边缘破裂以及凹模、凸模圆角处容易出现剪切断裂等[56]。传统成形极限曲线（FLC）的理论基础是颈缩失稳理论，在实验过程中施加的是线性载荷。但是先进高强钢在凹模、凸模圆角处开裂的极限应变远低于传统FLC的预测值且在断口处观察不到明显的减薄与颈缩。因此，在研究先进高强钢板料的断裂失效行为以及成形工艺制定方面，传统成形极限曲线的应用受限。相反，考虑了非线性应力与应变载荷历史的韧性断裂失效准则更为适用。该准则能更精确地预测板料的断裂行为，并为成形工艺的制定提供可靠依据。

Wang等[45]采用了5种非耦合韧性断裂模型（Brozzo、Oh、Rice-Tracey、Ko-Hh和LouHuh-2012），对QP980不同应力状态下的失效极限进行了研究，采用逆向工程的方法对本构模型的参数进行了优化，结果表明，LouHuh-2012模型的预测精度显著优于其他4种模型的。杨婷等[49]利用基于应变修正的MMC韧性断裂模型，预测了DP780钢板的成形极限曲线，随后通过半球形钢模的胀形实验，验证了该模型预测材料损伤和断裂性能的准确性。

金属材料的韧性断裂与微观尺度的应力状态、变形过程中的应变速率和温度变化等多因素相关。近年来，随着先进高强钢温、热成形技术的进步，研究者开始关注变形过程参数对材料塑性流动和损伤演变的综合影响，特别是应变速率和温度的耦合作用机理。魏星等[57]研究发现，随着应变速率从准静态逐渐上升到500 s−1，QP980和QP1180的屈服强度和抗拉强度均呈现出小幅增长的趋势，2种材料的均匀塑性变形区和断裂时的总延伸量随应变速率的提升而有不同程度的增大。Li等[58]研究发现，温度对DP800钢塑性的影响并非是单调的，当温度从20 ℃增大到120 ℃时，其断裂应变先减小后增大，其伸长率下降了27%，而当温度升高到300 ℃时，其伸长率又逐步增大，且比20 ℃时略有提高。

当前有关温度与应变速率等因素对先进高强钢力学性能的影响规律已有大量报道，且相关研究成果较为丰富，然而只有少数有关韧性断裂模型的研究考虑了应变速率与温度影响。郭玉琴等[59]在Freudenthal模型的基础上进行了修正，建立了适用于150～300 ℃温度范围的先进高强钢韧性断裂模型，该模型耦合了变形温度、应变速率与应变路径等因素的影响规律，他们将该模型导入有限元仿真软件中完成了算法实现，通过仿真计算预测了DP980钢的温热成形极限曲线，并通过高温杯突实验验证了该模型的准确性。王凯迪[60]基于MMC断裂失效模型，标定了DP780钢的断裂失效模型参数，通过数值模拟验证了修正后模型对DP780板料拉剪实验断裂预测的适用性，并通过数学语言描述了温度对断裂失效准则参数的影响规律。

以上研究表明，考虑了应变历史的韧性断裂准则能更准确地预测先进高强钢的断裂行为。目前已有多种韧性断裂准则模型被初步验证和应用，但这些模型仍存在一定局限性，对复杂应变载荷的考虑还不够全面和深入，与变形机理及微观本构的内在联系还需加强。在当前研究中，仅有少数模型考虑了温度和应变率对断裂的影响。为进一步提高韧性断裂准则的适用范围和预测精度，建立能够统一考虑复杂应变载荷历史、变形机理以及多场耦合的普适韧性断裂准则是未来研究的重点方向。充分利用多尺度建模理论、大数据与AI技术，有望实现从理论模型到实际工况的更好转换，使韧性断裂准则在先进高强钢设计和加工优化方面发挥更大作用。

表2 先进高强钢常用的韧性断裂模型

Tab.2 Commonly used ductile fracture models for advanced high-strength steel

5 结语

将先进高强钢应用于车身零件制造是实现汽车轻量化的重要手段，而高效、高精度的本构模型与韧性断裂模型在先进高强钢的应用发展中起到了关键作用。目前，在金属材料板料成形领域，本构模型的应用仍然以宏观唯象模型为主，无法体现其微观的变形机制。宏观力学性能是材料微观应力-应变演变的体现，随着力学性能优异的汽车新材料和成形工艺的不断发展，关联微-细-宏观的多尺度本构模型是未来的重要发展方向。当前针对板料成形过程中韧性断裂的研究，通常是在准静态以及常温条件下进行的，进一步深入研究先进高强钢冲压成形过程中温度软化、应变率强化和非均匀变形等因素对断裂机理的影响是非常必要的。通过开发普适性更强、能够考虑复杂耦合效应的韧性断裂模型，可以更准确地预测先进高强钢在冲压成形过程中的断裂行为，进而为金属冲压成形工艺的设计优化以及恶劣条件下材料断裂失效行为的研究提供更可靠的理论支持。

[1] ZHANG W, XU J. Advanced Lightweight Materials for Automobiles: A Review[J]. Materials & Design, 2022, 221: 110994.

[2] GHOSH T, KIM H C, KLEINE R, et al. Life Cycle Energy and Greenhouse Gas Emissions Implications of Using Carbon Fiber Reinforced Polymers in Automotive Components: Front Subframe Case Study[J]. Sustainable Materials and Technologies, 2021, 28: e00263.

[3] CZERWINSKI F. Current Trends in Automotive Lightweighting Strategies and Materials[J]. Materials, 2021, 14(21): 6631.

[4] 王存宇, 杨洁, 常颖, 等. 先进高强度汽车钢的发展趋势与挑战[J]. 钢铁, 2019, 54(2): 1-6.

WANG C Y, YANG J, CHANG Y, et al. Development Trend and Challenge of Advanced High Strength Automobile Steels[J]. Iron and Steel, 2019, 54(2): 1-6.

[5] HICKEY K. World Auto Steel[EB/OL]. Defining Steels. [2021-09-22]. https://ahssinsights.org/metallurgy/defining- steels/.

[6] LIMA R M C, TOLOMELLI F T S F, CLARKE A J, et al. Microstructural Characterization of A 1100 MPa Complex-phase Steel[J]. Journal of Materials Research and Technology, 2022, 17: 184-191.

[7] 沈左军, 武方方. QP980材料在A柱加强板上的仿真分析及试制[J]. 模具制造, 2020, 20(8): 32-34.

SHEN Z J, WU F f. Simulation Analysis and Application Research of QP980 Material on Automobile A-Pillar Reinforcement Plate[J]. Die & Mould Manufacture, 2020, 20(8): 32-34

[8] DAVAZE V, VALLINO N, FELD-PAYET S, et al. Plastic and Fracture Behavior of a Dual Phase Steel Sheet under Quasi-static and Dynamic Loadings[J]. Engineering Fracture Mechanics, 2020, 235: 107165.

[9] RAMÍREZ-RAMÍREZ J H, PÉREZ-GONZÁLEZ F A, ZAPATA-HERNÁNDEZ O J, et al. Failure Analysis of an Advanced High-strength Steel[J]. Engineering Failure Analysis, 2022, 131: 105893.

[10] 杜金亮, 冯运莉, 张颖隆. 新型汽车用Q&P钢的研究现状与发展趋势[J]. 材料导报, 2021, 35(15): 15189- 15196.

DU J L, FENG Y L, ZHANG Y L. Research Status and Development Trend of New Automotive Q&P Steel[J]. Materials Reports, 2021, 35(15): 15189-15196.

[11] NANDA T, SINGH V, SINGH V, et al. Third Generation of Advanced High-strength Steels: Processing Routes and Properties[J]. Proceedings of the Institution of Mechanical Engineers, Part L: Journal of Materials: Design and Applications, 2019, 233(2): 209-238.

[12] TAUB A, MOOR E, LUO A, et al. Materials for Automotive Lightweighting[J]. Annual Review of Materials Research, 2019, 49: 327-359.

[13] HE J, HAN G, FENG Y. Phase Transformation and Plastic Behavior of QP Steel Sheets: Transformation Kinetics-informed Modeling and Forming Limit Prediction[J]. Thin-Walled Structures, 2022, 173: 108977.

[14] ZENG L, SONG X, CHEN N, et al. A New Understanding of Transformation Induced Plasticity (TRIP) Effect in Austenitic Steels[J]. Materials Science and Engineering: A, 2022, 857: 143742.

[15] 冯怡爽, 韩国丰, 牛超, 等. QP980钢相变及力学行为研究[J]. 塑性工程学报, 2020, 27(11): 137-143.

FENG Y S, HAN G F, NIU C, et al. Research on Phase Transformation and Mechanical Behavior of QP980 Steel[J]. Journal of Plasticity Engineering, 2020, 27(11): 137-143.

[16] WANG Y W, MAKRYGIANNIS P, WU W, et al. Deformation Mode and Strain Path Dependence of Martensite Phase Transformation in QP980 Steel[J]. Journal of Materials Engineering and Performance, 2023, 32(14): 6175-6198.

[17] 徐祖耀. 马氏体相变的分类[J]. 金属学报, 1997, 33(1): 45-53.

XU Z Y. Classification of Martensite Transformation[J]. Acta Metallurgica Sinica, 1997, 33(1): 45-53.

[18] TALONEN J, HÄNNINEN H, NENONEN P, et al. Effect of Strain Rate on the Strain-induced γ→α′-marten­site Transformation and Mechanical Properties of Auste­n­itic Stainless Steels[J]. Metallurgical and materials transactions A, 2005, 36(2): 421-432.

[19] FENG W, WU Z, WANG L, et al. Effect of Testing Temperature on Retained Austenite Stability of Cold Rolled CMnSi Steels Treated by Quenching and Partitioning Process[J]. Steel Research International, 2013, 84(3): 246-252.

[20] ZOU D Q, LI S H, HE J. Temperature and Strain Rate Dependent Deformation Induced Martensitic Transformation and Flow Behavior of Quenching and Partitioning Steels[J]. Materials Science and Engineering: A, 2017, 680: 54-63.

[21] DING L, LIN J, MIN J, et al. Necking of Q&P Steel during Uniaxial Tensile Test with the Aid of DIC Technique[J]. Chinese Journal of Mechanical Engineering, 2013, 26(3): 448-453.

[22] 侯玉栋, 景财年, 丁啸云, 等. 应变速率对汽车用高强钢组织和性能的影响[J]. 金属热处理, 2020, 45(9): 71-76.

HOU Y D, JING C N, DING X Y, et al. Effect of Strain Rate on Microstructure and Properties of High Strength Steel for Automobile[J]. Heat Treatment of Metals, 2020, 45(9): 71-76.

[23] XIA P, VERCRUYSSE F, CELADA-CASERO C, et al. Effect of Alloying and Microstructure on Formability of Advanced High-strength Steels Processed via Quenching and Partitioning[J]. Materials Science and Engineering: A, 2022, 831: 142217.

[24] 邹丹青. QP钢应变诱发相变动力学模型及回弹特性研究[D]. 上海: 上海交通大学, 2018: 25-88.

ZOU D Q. Kinetics Model of Deformation Induced Martensitic Transformation and Springback Behavior for QP Steel Sheet Forming[D]. Shanghai: Shanghai Jiao Tong University, 2018: 25-88.

[25] CHEN P, LI X W, WANG P F, et al. Partitioning-related Microstructure Evolution and Mechanical Behavior in a δ-Quenching and Partitioning Steel[J]. Journal of Materials Research and Technology, 2022, 17: 1338-1348.

[26] GAO P, LI F, AN K, et al. Experimental and Modeling Study of Phase-specific Flow Stress Distribution in Intercritically Annealed Quenching and Partitioning Steels[J]. Crystals, 2022, 12(10): 1412.

[27] 单体坤, 张卫刚, 李淑慧. 耦合TRIP效应的TRIP型多相钢本构模型及其在冲压中的应用[J]. 上海交通大学学报, 2008(1): 73-77.

SHAN T K, ZHANG W G, LI S H. A Constitutive Model Coupling with TRIP Effect and Applying to the Sheet Metal Forming for TRIP Multi-phase Steels[J]. Journal of Shanghai Jiaotong University, 2008, 42(1): 73-77.

[28] MARTIN S, WEIDNER A, ULLRICH C, et al. Deformation Behaviour of TWIP Steels: Constitutive Modelling Informed by Local and Integral Experimental Methods Used in Concert[J]. Materials Characterization, 2022, 184: 111667.

[29] 丁磊, 林建平, 庞政, 等. 考虑TRIP效应的QP980超高强度钢多相本构模型[J]. 塑性工程学报, 2013, 20(4): 23-26.

DING L, LIN J P, PANG Z, et al. Multiphase Constitutive Model of Ultra-high Strength Steel QP980 Coupling with TRIP Effect[J]. Journal of Plasticity Engineering, 2013, 20(4): 23-26.

[30] 张文超. 计及相变的QP980钢的动态本构方程与断裂研究[D]. 宁波: 宁波大学, 2017: 33-55.

ZHANG W C. Study on Dynamic Constitutive Equation and Fracture of QP980 Steel Coupling with Phase Transformation[D]. Ningbo: Ningbo University, 2017: 33-55.

[31] ARLAZAROV A, BOUAZIZ O, MASSE J P, et al. Characterization and Modeling of Mechanical Behavior of Quenching and Partitioning Steels[J]. Materials Science and Engineering: A, 2015, 620: 293-300.

[32] CONNOLLY D S, KOHAR C P, MUHAMMAD W, et al. A Coupled Thermomechanical Crystal Plasticity Model Applied to Quenched and Partitioned Steel[J]. International Journal of Plasticity, 2020, 133: 102757.

[33] 赵辉, 彭艳, 石宝东. 金属材料各向异性本构模型研究进展[J]. 塑性工程学报, 2022, 29(10): 32-42.

ZHAO H, PENG Y, SHI B D. Research Progress on Anisotropic Constitutive Model of Metal Materials[J]. Journal of Plasticity Engineering, 2022, 29(10): 32-42.

[34] 彭剑, 周昌玉, 代巧, 等. 工业纯钛室温下的应变速率敏感性及Hollomon经验公式的改进[J]. 稀有金属材料与工程, 2013, 42(3): 483-487.

PENG J, ZHOU C Y, DAI Q, et al. Strain Rate Sensitivity of Commercially Pure Titanium TA2 at Room Temperature and Revising of Hollomon Empirical Formula[J]. Rare Metal Materials and Engineering, 2013, 42(3): 483-487.

[35] LUDWIK P. Elemente der Technologischen Mechanik[M]. Berlin: Springer-Verlag, 1909: 32.

[36] SWIFT H W. Plastic Instability under Plane Stress[J]. Journal of the Mechanics and Physics of Solids, 1952, 1(1): 1-18.

[37] FIELDS D S, BACKOFEN W A. Determination of Strain Hardening Characteristics by Torsion Testing[J]. Proc ASTM, 1957, 57: 1259-1272.

[38] 董伊康, 齐建军, 孙力, 等. 车用钢板材料硬化模型的适用性[J]. 机械工程材料, 2020, 44(10): 81-86.

DONG Y K, QI J J, SUN L, et al. Applicability of Hardening Model for Automobile Steels[J]. Materials for Mechanical Engineering, 2020, 44(10): 81-86.

[39] 李宏烨, 庄新村, 赵震. 材料常用流动应力模型研究[J]. 模具技术, 2009(5): 1-4.

LI H Y, ZHUANG X C, ZHAO Z. Research on Commonly Used Flow Stress Models for Materials[J]. Die and Mould Technology, 2009(5): 1-4.

[40] DZIALLACH S, BLECK W, BLUMBACH M, et al. Sheet Metal Testing and Flow Curve Determination under Multiaxial Conditions[J]. Advanced Engineering Materials, 2007, 9(11): 987-994.

[41] GOIJAERTS A M, GOVAERT L E, BAAIJENS F P T. Evaluation of Ductile Fracture Models for Different Metals in Blanking[J]. Journal of Materials Processing Technology, 2001, 110(3): 312-323.

[42] SAVAEDI Z, MOTALLEBI R, MIRZADEH H. A Review of Hot Deformation Behavior and Constitutive Models to Predict Flow Stress of High-entropy Alloys[J]. Journal of Alloys and Compounds, 2022, 903: 163964.

[43] XIA Y, DING C, LI Z, et al. Numerical Modeling of Stress-strain Relationships for Advanced High Strength Steels[J]. Journal of Constructional Steel Research, 2021, 182: 106687.

[44] 李奇涵, 王宝中, 高嵩, 等. 高强钢-铝合金材料的流动应力模型研究及应用[J]. 精密成形工程, 2021, 13(4): 121-126.

LI Q H, WANG B Z, GAO S, et al. Study on Flow Stress Model of High-strength Steel and Aluminum Alloy in Clinching[J]. Journal of Netshape Forming Engineering, 2021, 13(4): 121-126.

[45] WANG S, WANG Y, YU L, et al. Failure Modeling for QP980 Steel by a Shear Ductile Fracture Criterion[J]. Metals, 2022, 12(3): 452.

[46] 穆磊. 面向先进高强钢的韧性断裂预测模型研究与应用[D]. 北京: 北京科技大学, 2018: 26-69.

MU L. Study on a Ductile Fracture Prediction Model for Advanced High Strength Steel and Its Application[D]. Beijing: University of Science and Technology Beijing, 2018: 26-69.

[47] LOU Y, HUH H. Prediction of Ductile Fracture for Advanced High Strength Steel with a New Criterion: Experiments and Simulation[J]. Journal of Materials Processing Technology, 2013, 213(8): 1284-1302.

[48] 张赛军, 李康镇, 张昆, 等. 韧性断裂准则参数标定及其在DP590中的应用[J]. 哈尔滨工业大学学报, 2021, 53(1): 63-69.

ZHANG S J, LI K Z, ZHANG K, et al. Parameter Calibration of Ductile Fracture Criterion and its Application on DP590[J]. Journal of Harbin Institute of Technology, 2021, 53(1): 63-69.

[49] 杨婷, 熊自柳, 孙力, 等. 汽车用先进高强钢韧性断裂模型的研究与应用进展[J]. 锻压技术, 2021, 46(1): 10-16.

YANG T, XIONG Z L, SUN L, et al. Research and Application Progress on Ductile Fracture Model of Advanced High-strength Steel(AHSS) for Automotive[J]. Forging & Stamping Technology, 2021, 46(1): 10-16.

[50] 贾哲, 穆磊, 臧勇. 金属塑性成形中的韧性断裂微观机理及预测模型的研究进展[J]. 工程科学学报, 2018, 40(12): 1454-1467.

JIA Z, MU L, ZANG Y. Research Progress on the Micro-mechanism and Prediction Models of Ductile Fracture in Metal Forming[J]. Chinese Journal of Engineering, 2018, 40(12): 1454-1467.

[51] 马宏越, 肖纳敏, 钱鹏, 等. 非耦合韧性断裂准则及其在航空金属材料中的应用[J]. 航空材料学报, 2021, 41(2): 16-31.

MA H Y, XIAO N M, QIAN P, et al. Uncoupled Ductile Fracture Criterion and Its Application in Aeronautical Metallic Materials[J]. Journal of Aeronautical Materials, 2021, 41(2): 16-31.

[52] BAI Y, WIERZBICKI T. Application of Extended Mohr-Coulomb Criterion to Ductile Fracture[J]. International Journal of Fracture, 2010, 161(1): 1-20.

[53] LOU Y, HUH H, LIM S, et al. New Ductile Fracture Criterion for Prediction of Fracture Forming Limit Diagrams of Sheet Metals[J]. International Journal of Solids and Structures, 2012, 49(25): 3605-3615.

[54] LOU Y, YOON J W. Anisotropic Ductile Fracture Criterion Based on Linear Transformation[J]. International Journal of Plasticity, 2017, 93: 3-25.

[55] MU L, ZANG Y, WANG Y, et al. Phenomenological Uncoupled Ductile Fracture Model Considering Different Void Deformation Modes for Sheet Metal Forming[J]. International Journal of Mechanical Sciences, 2018, 141: 408-423.

[56] 李梅, 赵亦希, 胡星, 等. 先进高强度双相钢汽车板剪切断裂实验[J]. 上海交通大学学报, 2011, 45(11): 1695-1699.

LI M, ZHAO Y X, HU X, et al. Experimental Study of Shear Fracture on Advanced High Strength Dual Phase Steels[J]. Journal of Shanghai Jiaotong University, 2011, 45(11): 1695-1699.

[57] 魏星, 钟勇, 彭周, 等. QP980和QP1180的塑性变形及断裂行为[J]. 塑性工程学报, 2021, 28(12): 103-114.

WEI X, ZHONG Y, PENG Z, et al. Plastic Deformation and Fracture Behavior of QP980 and QP1180[J]. Journal of Plasticity Engineering, 2021, 28(12): 103-114.

[58] LI S H, HE J, GU B, et al. Anisotropic Fracture of Advanced High Strength Steel Sheets: Experiment and Theory[J]. International Journal of Plasticity, 2018, 103: 95-118．

[59] 郭玉琴, 王帅, 朱新峰, 等. B340/590DP钢温热成形破裂准则提出及成形极限预测[J]. 塑性工程学报, 2015, 22(3): 38-43.

GUO Y Q, WANG S, ZHU X F, et al. Proposal of Warm Forming Fracture Criterion and Forming Limit Prediction of B340/590DP Steel[J]. Journal of Plasticity Engineering, 2015, 22(3): 38-43.

[60] 王凯迪. 先进高强度双相钢车身板温成形破裂失效准则研究[D]. 淄博: 山东理工大学, 2021: 7-52.

WANG K D. The Study on Fracture Failure Criterion of Advanced High Strength Dual-phase Steel Body Panel during Warm Forming[D]. Zibo: Shandong University of Technology, 2021: 7-52.

Research Progress on Constitutive Model and Ductile Fracture Model of Advanced High Strength Steel for Automotive Applications

CHAO Chengxin1, YU Qiang1,2*, LI Qiu1

(1. College of Mechanical Engineering, Tianjin University of Technology and Education, Tianjin 300222, China; 2. State Key Laboratory for Manufacturing Systems Engineering, School of Mechanical Engineering, Xi'an Jiaotong University, Xi'an 710049, China)

Lightweight is a common topic in the whole industry chain of automobile industry. Increasing the proportion of high strength steel and reducing the amount of steel are effective means to achieve lightweight of automobiles. Sufficient research on the constitutive model and the ductile fracture model of advanced high strength steel can help improve the accuracy of crack analysis and prediction of advanced high strength steel, thereby promoting the engineering application process of advanced high strength steel. In the prevent research of advanced high strength steel, scholars usually use a linear combination of multiple strain strengthening models to construct constitutive models, or conduct multi-scale analysis combining microstructure and macroscopic mechanical behavior to establish constitutive models. The work aims to calibrate the parameters of ductile fracture models through quasi-static tensile experiments under various stress states, using a mixture of simulation and experimental methods. With quenching partitioning steel (QP) steel in the third generation of advanced high-strength steel as the main object, the preparation process, material properties, and related research progress were introduced. And the research status of constitutive models for QP steel was introduced. The newly developed non-coupled ductile fracture model was also introduced, along with the application status of the ductile fracture model considering the influence of stress triaxiality and Lode angle parameters on advanced high strength steel.Finally, the future development directions of constitutive models and ductile fracture models were pointed out.

lightweight; advanced high strength steel; stamping forming; constitutive model; ductile fracture model

10.3969/j.issn.1674-6457.2024.01.009

O346.1；TG142.1

A

1674-6457(2024)01-0077-10

2023-07-08

2023-07-08

天津市科技计划（18JCTPJC64500）

The Science and Technology Plan Project of Tianjin (18JCTPJC64500)

巢成新, 于强, 李秋. 汽车用先进高强钢本构模型与韧性断裂模型研究进展[J]. 精密成形工程, 2024, 16(1): 77-86.

CHAO Chengxin, YU Qiang, LI Qiu. Research Progress on Constitutive Model and Ductile Fracture Model of Advanced High Strength Steel for Automotive Applications[J]. Journal of Netshape Forming Engineering, 2024, 16(1): 77-86.

（Corresponding author）