强震作用下特高拱坝动力响应及损伤特征研究

高志良，黄会宝，2，沈定斌，彭 涛

(1.国能大渡河流域水电开发有限公司,四川 成都 610041;2.四川大学 水利水电学院,四川 成都 610065)

1 引 言

随着我国水电能源开发战略的实施,一座座水电站在西南地区建成,其中许多水利枢纽都采用拱坝作为挡水建筑物[1-6],且大多拱坝坝体高度在200 m以上,属于特高拱坝。另外由于西南地区地处欧亚和印度板块接壤的位置,地质构造活动十分活跃,且新生代以来一直受到青藏高原抬升构造运动的影响,地壳运动强烈,地壳持续变形、震级大、烈度高、发震频繁,区域稳定性差,这导致拱坝坝区多数位于高地震烈度区,例如：乌东德(基本地震烈度7°)、溪洛渡(基本地震烈度8°)、白鹤滩(基本地震烈度8°)及大岗山(基本地震烈度8°)等。因此,拱坝抗震安全也成为中国水利水电枢纽工程建设和运行中无法回避的关键问题[7]。

混凝土拱坝在地震作用下的动力分析一直是拱坝安全评定的前沿问题,主要涉及强震作用下的坝体局部材料损伤和整体结构的渐进破坏,以及坝体整体的非线性动力特性分析等。研究人员考虑各类人工边界来研究地基辐射阻尼对拱坝地震响应分析的影响[8-10],有效模拟了地震波动能量向无限远处的逸散情况。人工边界方法计算效率显著提高,易与有限元或有限差分等方法相结合,并能够处理非线性问题,被广泛地研究及应用[11]。Chopra[12]对拱坝地震动力响应分析中考虑的因素进行了分析讨论,认为水库和基岩域的半无界尺寸、坝-水相互作用、坝-基岩相互作用、水的可压缩性、水库边界的水动力波吸收以及坝体-基岩接触面岩土运动的空间变化都是拱坝地震动力响应分析应该考虑的主要因素,同时探究了坝体混凝土和基岩的阻尼值的选取。Wang等[13]考虑坝体-库水-地基相互作用,采用黏弹性边界对拱坝地震损伤进行研究,通过增量动力分析方法探究了拱坝遭受地震破坏的可能性。Løkke等[14]将考虑黏滞阻尼边界的直接有限元法用于三维大坝—地基岩石系统,采用标准黏滞阻尼作为人工边界,通过对Morrow Point 拱坝进行动力响应分析,验证了程序在多因素影响下的拱坝非线性地震响应分析上的有效性。Jin等[15]研究了地基模型的主要特性对拱坝地震动力响应的影响,在考虑了地基辐射阻尼效应的情况下,对模型截断尺寸、材料阻尼和地基不均性等关键因素进行了分析。Pan等[16]提出了混凝土塑性损伤本构关系与收缩缝接触边界模拟相结合的综合非线性模型,研究了拱坝在强震作用下的损伤开裂机制,比较了不同的地震输入机制对拱坝损伤开裂的影响。陈建云等[17]探究了强震作用下的拱坝损伤整体判别指标,提出了拱坝整体抗震性能3个阶段水平。Alembagheri等[18]通过增量动力分析方法对Morrow Point拱坝的地震损伤特征进行了研究,分析了不同地震强度水平下的坝体损伤情况,提出了拱坝损伤体积比评价指标。Xu等[19]研究了不同地震峰值加速度作用下的白鹤滩拱坝非线性动力响应,对拱坝的损伤分布和位移等动力响应特征进行了统计,通过分析拱坝局部损伤和整体损伤发展情况,对损伤体积比变化情况进行了研究。Chen等[20]通过整体损伤体积比和损伤面积比来确定大坝受损严重的部位,并探究了损伤指标与监测指标之间的相关性。

拱坝在强烈地震扰动下,坝体可能发生复杂的非线性变形,直到最终被破坏,但目前实际案例较少。多数研究不能很好地反映坝体在强震作用下从局部损伤萌生、损伤破坏加剧到整体宏观开裂破坏的过程,且数值模型大多采用均质材料,而拱坝混凝土属于非均质准脆性材料[21]。如果能够考虑混凝土拱坝的破坏过程和破坏模式,并同时考虑材料的非均质性,对拱坝的地震响应分析则会更真实、更全面。真实破裂过程分析程序(Realistic Failure Process Analysis 3D, RFPA3D)基于有限元基本理论,充分考虑岩石或混凝土材料破裂过程中伴随的非线性、非均匀性及各向异性等特点,能够较好地展示岩体或混凝土材料可能存在的损伤破坏形态,这为拱坝潜在失稳破坏过程的研究提供了新思路。本文以大岗山水电站特高拱坝为研究对象,采用基于RFPA3D开发的RFPA3D动力版(RFPA3D-Dynamics),开展特高拱坝动力响应特性研究,分析地震作用下坝体变形、应力变化规律,尝试圈定坝体震害损伤的位置与范围,探讨了坝体在强震作用下潜在的损伤、破坏及失稳模式。

2 工程概况

大岗山水电站位于大渡河中游上段,雅安市石棉县挖角乡境内。工程枢纽挡水建筑物为混凝土双曲拱坝,最大坝高210 m,属于特高拱坝。坝区正常蓄水位1 130 m,相应库容7.42亿m3,电站装机2 600 MW,为大渡河流域水能开发的骨干工程。大岗山拱坝坝区处于北东向的龙门山构造带、北西向鲜水河构造带、南北向的大渡河和安宁河断裂带三组不同方向的断裂构造带交汇的“Y”型构造区的“三岔口”,如图1所示。大岗山拱坝抗震设防类别为甲类,坝址工程场地地震基本烈度为8°。坝址区100年超越概率2 %设计地震的基岩水平峰值加速度为557.5 cm/s2,即0.557 5 g;大岗山水电站坝高库大,地震设防水平很高,坝体遭遇强烈地震时的抗震安全问题极为重要,因此对于大岗山拱坝这样地处高地震烈度区的大型挡水建筑物而言,对其进行地震动力响应研究十分必要。

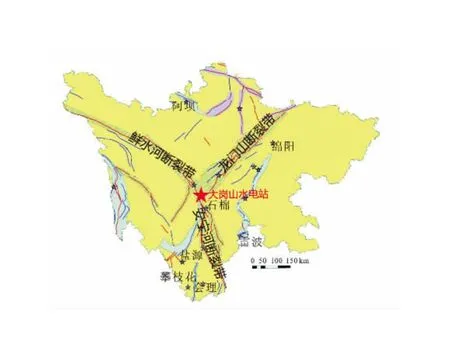
图1 大岗山坝区断裂带概况Fig.1 Overview of the fracture zone in the Dagangshan dam

3 计算方法及条件

3.1 坝体混凝土材料非均匀性的实现

RFPA3D考虑了材料的非均匀性,并利用均质度这一概念将材料力学参数赋予各个模型单元,认为宏观破坏是微观单元破坏的一种积累。在RFPA3D实际计算过程中,一般使模型内部单元的各项材料力学性质均服从Weibull分布,不同均值度下模型各单元力学性质分布规律如图2所示,Weibull分布的基本理论如下[22]：

(1)

图2 不同均质度下模型各单元力学参数分布规律示意图Fig.2 Schematic diagram of the distribution pattern of mechanical parameters in each unit of the model under different homogeneities

式中：m表示分布函数的形状参数,其物理意义反映了岩石或混凝土材料的均匀性(即均质度);α表示模型单元的力学参数,本文主要考虑了材料的密度、泊松比、弹性模量、抗压及抗拉强度受均质度的影响;α0表示单元力学参数的平均值;φ(α)为力学参数α的统计分布密度。从图2可以看出,当m值越小,单元的力学参数离散分布越明显,岩石或混凝土材料越不均匀。随着m值的不断增大,单元的力学参数集中在一小段区域内,表明材料的均匀性越高。在本文研究中,均质度m取值为8。

3.2 RFPA3D-Dynamics 动力算法

RFPA3D-Dynamics在充分考虑坝体材料非均匀性的基础之上,引入动力计算方法,根据Hamilton变分原理,利用有限元法进行空间离散处理之后,动力方程具有以下形式[23]：

(2)

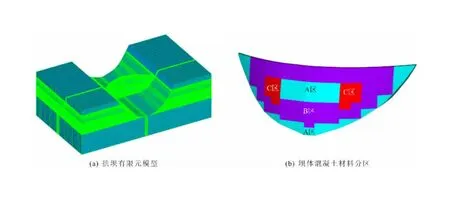
图3 大岗山拱坝有限元模型Fig.3 Finite element model of Dagangshan arch dam

在时间域内,求解式(2)的方法有很多,RFPA3D-Dynamics采用最简单也是最常用的一种隐式积分法：Newmark方法。在Newmark方法中,积分在一个时间间隔Δt上进行,而且依据递推关系,上一个时刻的位移值及其偏导数可用于确定下一时刻的值,因此Newmark方法保持方程求解的无条件稳定[23]。

3.3 材料损伤破坏表征

RFPA3D通过最大拉应变准则和摩尔库伦剪切破坏准则判断单元是否损坏[24],同时RFPA3D基于弹性损伤理论,采用带有残余强度的弹脆性损伤本构,通过定义损伤变量D值来表征岩体或者混凝土的损伤状态。当D=0时,表示单元未损伤;当D=1时,表示岩体单元完全损伤,即此时岩体或混凝土材料开裂并形成宏观裂缝。当数值模型中的单元受到拉伸破坏时,单元损伤如式(3)表示[24]：

(3)

式中,λ为单元残余强度系数;εt0、εtu分别为弹性极限所对应的拉伸应变和单元的极限拉伸应变。

当数值模型中的单元受到压剪破坏时,单元损伤由式(4)表示[24]：

(4)

式中,λ为单元残余强度系数;εc0为弹性极限所对应的单元压缩应变阈值。

3.4 计算模型

根据大岗山拱坝体型设计参数,建立大岗山拱坝有限元数值模型,模型左右岸长度1 400 m,上下游宽度850 m,竖向高度470 m,其中坝体高度210 m,坝顶高程1 135 m,边坡顶部高程1 185 m,坝底基岩深度取210 m。计算模型采用完全六面体网格划分见图3(a),模型单元总数为1 407 856个,其中坝体单元数量为724 480个,坝体单元尺寸平均为1 m×1 m×1 m。另外,依据坝体混凝土材料实际分区情况(图3b),对坝体不同区域分区,并赋予相应的力学参数(表1)。有限元模型利用ANSYS建立,然后利用ANSYS与RFPA3D-Dynamics软件的接口程序,将有限元模型节点、单元等数据信息导入到RFPA3D-Dynamics中开展计算。

表1 有限元模型材料参数

3.5 地震荷载及计算工况

依据大岗山水电站坝址地震危险性分析,得到相当于100年期限内超越概率为2 %的拱坝坝址基岩设计水平向地震峰值加速度PGA(Peak Ground Acceleration)为0.557 5g,竖向峰值地震加速度则取水平向的2/3,以此作为大岗山拱坝设计地震波。设计地震波加速度三向时程曲线见图4,计算时间步长为0.01 s,阻尼比为5 %,动力边界采用三维一致性黏弹性人工边界。以设计地震波加速度波形作为输入地震波波形,其地震峰值加速度定义为1.0 PGA。在考虑上游正常蓄水位(1 130 m)的情况下,计算并分析了1.0 PGA、1.5 PGA下的大岗山拱坝应力场、位移场、损伤场的演化规律。

图4 设计地震波加速度三向时程曲线Fig.4 Three-component acceleration curve of the design seismic wave

4 数值计算

4.1 静水荷载作用下拱坝工作性态

大岗山拱坝死水位为1 120 m,正常蓄水位为1 130 m。在考虑自重、上游蓄水压力情况下,首先针对运行期在静水荷载作用下的拱坝工作性态开展分析,规定横河向位移指向左岸为正,顺河向位移指向上游为正,受拉为正,受压为负。

4.1.1 拱坝最大主应力

图5为拱坝在1 120 m及1 130 m水位下的最大主应力分布情况,图5(a)表明在水位1 120 m情况下,拱坝整体处于受压状态,主要受拉区域位于上游坝趾,拉应力最大值为4.28 MPa,坝体最大主应力分布均匀,呈梯度变化,沿高程从下往上呈减小趋势。图5(b)为水位1 130 m时的拱坝最大主应力分布特征,坝体整体处于受压状态,最大主应力分布均匀,拉应力最大值为6.2 MPa,拉应力水平较1 120 m水位时的应力略有增加,这主要是因为拱坝在高水位下,整体向下游变形,导致坝趾区域拉应力水平上升。

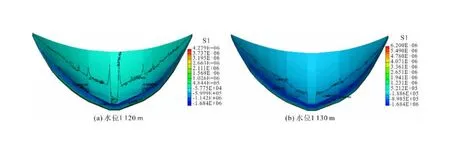
图5 静水荷载下拱坝最大主应力云图(单位：Pa)Fig.5 Maximum principal stresses in arch dams under hydrostatic loading (unit：Pa)

4.1.2 拱坝最小主应力

图6为拱坝在1 120 m及1 130 m水位下的最小主应力分布情况。在水位1 120 m时(图6a),拱坝整体处于受压状态,压应力分布较为均匀,压应力最大值为-9.77 MPa,位于下游坝踵区域。当水位上升至1 130 m时(图6b),拱坝整体压应力分布情况与水位1 120 m时的情况基本相同,但下游坝踵的压应力集中区域略有扩大,压应力最大值增大至-10.49 MPa,这也是因为上游水荷载的作用,导致拱坝向下游变形,坝踵区域受到挤压,导致坝踵区域压应力水平上升。

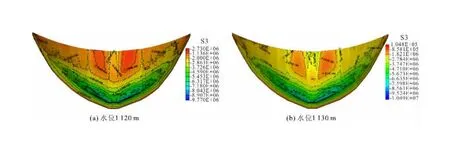
图6 静水荷载下拱坝最小主应力云图(单位：Pa)Fig.6 Minimum principal stresses in arch dams under hydrostatic loading (unit：Pa)

4.1.3 拱坝顺河向位移变化

图7给出不同水位情况下坝顶及拱冠梁顺河向位移变化情况。由图7(a)可知,拱坝在水位1 120 m及1 130 m情况下,整体变形协调且呈U型变化,顺河向位移由坝体中心向两岸逐渐减小,顺河向位移最大值均出现在拱冠梁顶部。由图7(b)可知,拱坝在各水位工况下,拱冠梁顺河向位移整体指向下游,且沿拱冠梁自上而下逐渐减小。表明了大岗山拱坝横河向和顺河向位移变化均符合拱坝一般变形规律,即在高水位情况下,拱坝横河向变形指向岸坡,顺河向位移指向下游。

图7 静水荷载下拱坝坝顶及拱冠梁顺河向位移变化规律Fig.7 Variation of stream displacement of arch dam crest and crown cantilever under hydrostatic loading

大岗山拱坝蓄水至正常蓄水位1 130 m之后,坝顶1 135 m高程多个监测点的竖向沉降位移值如图8所示,包括了现场外观变形监测点实测竖向沉降平均值以及数值模拟结果,可以看出,坝顶3处拱坝外观变形观测点TP10-1、TP14-1以及TP19-1的实测竖向沉降平均值分别为10.1 mm、15.5 mm以及10.7 mm,相应各监测点的数值模拟结果分别为9.4 mm、16.1 mm、9.8 mm,且拱坝竖向沉降量从拱坝中心向两岸逐渐减小。数值模拟结果与现场实测值基本吻合,验证了数值计算模型的合理性。在此基础之上,进一步开展地震作用下大岗山拱坝动力响应研究。

图8 正常蓄水位下拱坝竖向位移Fig.8 Vertical displacement of arch dam under normal storage level

图9 拱坝最大主应力包络云图(1.0 PGA,单位：Pa)Fig.9 Maximum principal stress diagram for arch dams (1.0 PGA,unit：Pa)

4.2 1.0 PGA工况下拱坝动力响应

4.2.1 拱坝最大主应力

图9为拱坝在设计地震波(1.0 PGA)下的最大主应力分布云图。在t=2 s时,拱坝整体处于受压状态,局部拉应力集中区域主要位于上游坝踵区域,最大拉应力4.94 MPa。在t=5 s时,拱坝拉应力集中区域分别出现在左右半拱上部区域,集中区域的拉应力水平在1.6 MPa左右。在t=8 s时,拱坝拉应力集中区域主要在左半拱上部靠近拱冠梁的区域以及左拱端区域,应力集中区域的拉应力水平在1.88 MPa～2.30 MPa之间。在t=10 s时,随着地震波的衰减,拱坝应力分布趋向均匀,局部拉应力集中区域主要位于上游坝踵区域,最大拉应力4.27 MPa。

4.2.2 拱坝最小主应力

图10为拱坝在设计地震波(1.0PGA)下的最小主应力分布云图。在t=2 s时,局部压应力集中区域主要位于下游坝趾区域,最大压应力-9.69 MPa(负值表示受压)。在t=5 s时,拱坝压应力集中区域未发生转移,仍然分布在下游坝趾区域,最大压应力值为-12.38 MPa。在t=8 s时,拱坝下游坝趾压应力集中区域扩大,最大压应力值为-11.09 MPa。在t=10 s时,拱坝整体处于受压状态,保持稳定。从最大及最小主应力分布情况分析,在1.0 PGA情况下,拱坝应整体应力调整能力良好,在经历地震后,能够保持稳定状态。

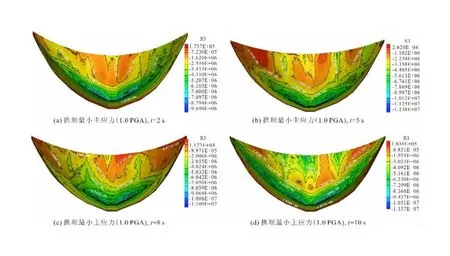
图10 拱坝最小主应力包络云图(1.0 PGA,单位Pa)Fig.10 Minimum principal stress diagram for arch dams (1.0 PGA,unit：Pa)

4.2.3 拱坝顺河向位移

图11拱坝顺河向位移分布较均匀,自上而下位移值逐渐减小,主要位移变形区域位于拱坝半拱上部的1/2处,变形指向下游,最大顺河向位移值-66.65 mm;在地震期间,拱坝坝顶各监测点在地震0～5 s期间,顺河向位移变化量较小,拱坝整体变形协调。在t=10 s时,拱坝顺河向变形向下游成W形,左右半拱中间位置的顺河向位移较大,但无明显位移突变现象,这说明坝体在1.0 PGA工况下,具有较好的变形协调能力。

图11 拱坝坝顶顺河向位移变化(1.0 PGA)Fig.11 Variation of stream displacement of arch dam crest (1.0 PGA)

4.2.4 坝体损伤演化

图12为拱坝在1.0 PGA下的坝体损伤情况,可以看出,在整个地震期间,坝体没有发生大规模的损伤区域,仅在拱坝拱冠梁顶部及左拱端发生少量离散损伤点(图12d),损伤点未发生扩展及贯通现象,损伤值在0.24～0.29之间,损伤值较小,这对于大体量混凝土结构而言,损伤几乎可以忽略不计,拱坝在1.0 PGA情况下,整体应力状态良好,变形协调,地震作用对大坝不会造成较大的安全隐患。

4.3 1.5 PGA工况下拱坝动力响应

4.3.1 拱坝最大主应力

图13为拱坝在1.5 PGA下的最大主应力分布云图。在t=2 s时,拱坝整体处于受压状态,主要受拉区位于上游坝踵,最大拉应力值为5.93 MPa;在t=5 s时,拱坝拉应力集中区域出现在右半拱上部,集中区域的拉应力最大值在5.34 MPa。在t=8 s时,拱坝拉应力集中区域转移到左右半拱上部1/2处,拉应力最大值为4.0 MPa。在t=10 s时,拱坝拉应力区域范围扩大,但整体拉应力水平较低,这是坝体因地震作用发生显著损伤破坏后,应力释放导致的。

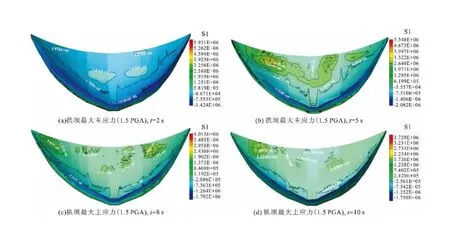
图13 拱坝最大主应力包络云图(1.5 PGA,单位：Pa)Fig.13 Maximum principal stress diagram for arch dams (1.5 PGA,unit： Pa)

4.3.2 拱坝最小主应力

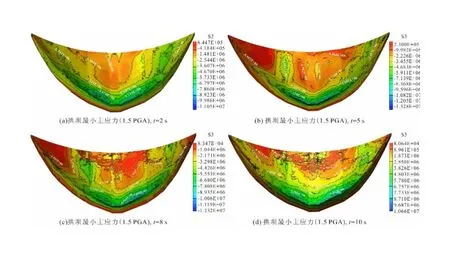
图14 拱坝最小主应力包络云图(1.5 PGA,单位：Pa)Fig.14 Minimum principal stress diagram for arch dams (1.5 PGA,unit：Pa)

图14为拱坝在1.5 PGA下的最小主应力分布云图。在t=2 s时,局部压应力集中区域主要位于下游坝趾区域,最大压应力值-11.05 MPa。在t=5 s时,拱坝压应力集中区域在下游坝趾区域扩大,最大压应力值为-13.28 MPa,但上部受压区域减小,受拉区占据左右半拱大部分中上部区域。在t=8 s时,拱坝坝体中下部仍然处于受压状态,但在坝体的拱冠梁、左右半拱上部区域以及左右拱端出现了多条竖向条带状拉应力集中区域,拉应力水平较低,这说明该区域已经发生了损伤破坏,坝体单元之间产生宏观裂缝,在地震作用下未能保持闭合状态。在t=10 s时,在拱冠梁及左半拱上部区域的条带状应力集中区域更为显著,左右拱端的条带状拉应力集中区域也进一步扩展增大,这主要是因为坝体在产生宏观裂缝之后,该区域张拉变形导致的。

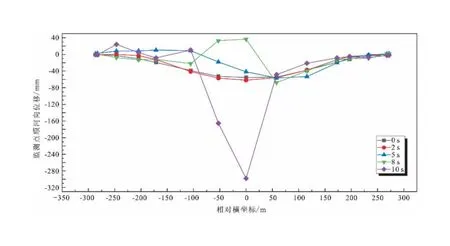
图15 拱坝坝顶顺河向位移变化(1.5 PGA)Fig.15 Variation of stream displacement of arch dam crest (1.5 PGA)

4.3.3 拱坝顺河向位移

图15为拱顶各特征点在1.5 PGA情况下的顺河向位移变形,可以看出坝体在地震历时5 s之后,开始在拱冠梁左右两侧发生显著的位移,右半拱向上游变形,左半拱向下游变形,这会导致坝体上部区域因反复拉伸而破坏;t=10 s时,拱坝在拱冠梁顶部发生位移突变,位移突变量达到240 mm以上,说明此时该区域坝体混凝土已经发生了明显的开裂错动。在1.5 PGA情况下,坝体发生显著位移突变现象,坝体已不能通过自身的变形调整维持相对稳定状态。

4.3.4 拱坝损伤演化

图16为拱坝在1.5 PGA工况下的坝体损伤演化情况,结合主应力变化情况进行分析,首先出现损伤的部位发生在左右半拱的中上部区域,左半拱损伤区域要大于右半拱,同时左拱端相比于右拱端也出现了较为明显的损伤裂缝。在t=8 s时,D=1的损伤单元在拱坝的拱冠梁顶部和左右半拱顶部区域呈带状分布,表明坝体已经发生了损伤开裂现象,且多条竖向裂缝贯通上下游坝面,而竖向裂缝之间因水平裂缝的萌生也已相互连通;此时在左右拱端下游面也因损伤区域扩大而形成明显的条带状裂缝,并扩展至坝体中部位置,但左右拱端的裂缝并未出现上下游贯通现象。t=10 s时,坝体损伤程度相较于8 s时并未有显著变化,这说明损伤区域基本成形,裂缝贯通后并未进一步扩展。可以看出,与1.0 PGA工况对比,在1.5 PGA工况下,坝体发生显著的损伤破坏,且破坏后的坝体区域位移突变明显,易受损破坏区域主要是坝体中上部区域以及左右拱端。坝体下部区域由于自身混凝土体量大的原因能够保持相对稳定,但坝体中上部区域有潜在的失稳风险。

图16 拱坝损伤演化规律下游侧视图(1.5 PGA)Fig.16 Downstream side view of arch dam damage evolution law (1.5 PGA)

4.4 坝体声发射及累计声发射能量释放

拱坝结构在动力扰动作用下发生变形,势必会伴随着能量的输入、积聚、释放和转移,因此拱坝坝体结构的破坏可以看作能量驱动下的一种状态失稳现象。因此拱坝在发生损伤破坏过程中,混凝土内部累积的应变能以弹性波的形式进行释放,即产生声发射事件(Acoustic Emission,AE),并释放能量,分析声发射事件及释放能量的累计变化规律,可以衡量损伤破坏程度。

在RFPA中,声发射事件数量由破坏单元的数量给出,破坏单元所释放的应变能作为声发射能量[25]。图17为不同工况下坝体声发射事件数及累计声发射能量变化规律,在1.0 PGA工况下,拱坝声发射事件整体较少,且并未在某一时间段内集中发生,最大声发射事件数为87个;分析图17(a)累计声发射能量可以看出,声发射能量在地震期间没有突增现象,最大累计释放能量为12.95 J,整体上累计声发射能量增长缓慢,且在地震后保持平稳,结合图12,说明拱坝在1.0 PGA工况下坝体无较大规模损伤发生,并且在地震过后能够保持安全稳定状态。在1.5 PGA工况下,拱坝在0～5 s内声发射事件数量较少;在5～8 s期间,声发射事件数量激增,声发射能量也迅速增长,结合图16分析,此时间段是坝体产生大规模损伤的阶段,此时单步最大声发射事件数量达到1 206个,远远超过1.0 PGA的情况;在8 s之后,声发射事件数量明显减小,主要是因为地震波衰减和损伤区域基本成形导致的。分析图17(b)累计声发射能量可以看出,在地震初期(0～2 s),声发射能量基本为0;在2～5 s时,随着坝体开始出现损伤,声发射能量逐渐增加;在5～8 s时,累计声发射能量随着坝体出现宏观开裂而激增;在8 s之后,坝体应力得到有效释放,累计声发射能量趋于平稳,此时最大累计释放能量为130 J,同时坝体损伤区域基本成形,不再发生进一步的破坏损伤。

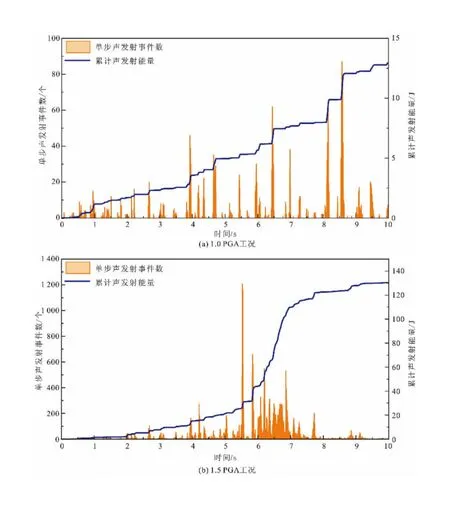
图17 不同工况下坝体声发射事件数及累计声发射能量变化Fig.17 Variation of the number of AE events and the evolution of AE energy of dam under different conditions

5 结论

1)大岗山拱坝在静水荷载作用下,整体变形协调,顺河向和横河向位移均符合拱坝一般的变形规律;在上游库水作用下,拱坝拉应力集中区域出现在上游坝踵区域,压应力集中区域出现在下游坝趾区域,但应力水平在正常范畴之内。

2)大岗山拱坝在设计地震波(1.0 PGA)下整体变形协调,符合大坝一般变形规律,在地震作用下坝体无位移突变现象。在地震作用下,最大顺河向位移发生在坝顶右半拱约1/2处,最大顺河向位移值为-66.65 mm左右。坝体无较大规模损伤区域出现,仅在坝体下游面出现零星损伤点,损伤值在0.24～0.29之间,对于拱坝正常运行状态无影响。

3)在1.5 PGA工况下探究了大岗山拱坝损伤演化规律,坝体出现较大规模损伤,损伤位置主要出现在拱冠梁顶部及坝体左右半拱中上部区域,综合判断,提出大岗山高拱坝潜在失稳区域主要是在拱坝坝体中上部区域及拱冠梁顶部区域,这为掌握大岗山拱坝在正常运行期间的重点安全监测区域提供了一定的参考价值。

4)通过声发射事件数和累计发射能量能够判断坝体损伤状态。地震期间声发射数量较少,累计释放能量增长缓慢,说明坝体整体稳定,无大规模损伤区域发生;若声发射数量激增,累计声发射能量增长迅速,说明坝体在地震作用下发生损伤破坏,坝体应力得到有效释放。