基于改进磷虾群算法的风-光-水-火联合系统优化调度
朱 戈,李华南,刘 闯
(1.雅砻江流域水电开发有限公司,四川 成都 610051;2.国网湖北省电力有限公司荆门供电公司,湖北 荆门 448000)
0 引言
在能源危机和环境污染的双重背景下,风电、光伏产业迅速发展, 传统化石能源正在被可再生能源替代,风能、太阳能等可再生能源具有明显的随机波动性,无法持续稳定地输出电能[1-2]。 我国水电资源丰富,水力发电调峰效果好,可以很好地弥补风光发电功率不稳定的缺陷,提高可再生能源的消纳[3]。 因此,对风-光-水-火联合系统的优化调度进行研究,对于提高电力系统稳定性和降低碳排放量具有重要意义[4-5]。
针对联合系统优化调度问题, 国内外专家学者进行了大量研究,也提出了许多优化调度方法。邵磊等对含抽水蓄能、风电、光伏和火电的联合系统优化调度进行了研究, 建立了联合系统多目标优化调度模型,采用Yalmip 工具箱对模型进行求解,获得了低碳经济的联合系统运行方案[6]。 罗远翔等采用长短2 种不同时间尺度综合衡量风-光-火-蓄联合系统的运行成本,以运行成本最小为目标函数,建立了风-光-火-蓄联合系统的两阶段动态调度模型,并用具体算例验证了该模型的有效性[7]。 印去刚等为了提高风-光-水联合系统运行的经济性,建立了以收益最大为目标函数的调度模型, 采用改进灰狼算法对模型进行求解, 并通过算例分析验证了模型的有效性[8]。 现有的联合系统优化调度模型只考虑了系统运行的经济性,而忽略了弃风、弃光带来的环境惩罚成本, 兼顾经济性和环保性的风-光-水-火联合系统优化调度问题有待进一步研究。 笔者以风-光-水-火联合系统综合成本最小为目标函数,综合考虑各种约束条件, 建立了风-光-水-火联合系统的优化调度模型, 采用改进磷虾群算法对模型进行求解,并通过算例分析,对该模型的实用性和优越性进行验证。
1 风-光-水-火联合系统优化调度模型
1.1 目标函数
为了提高可再生能源的利用率,减少弃风、弃光量, 本研究在风-光-水-火联合系统运行成本中引入弃风、弃光惩罚成本,并以综合成本最小为目标函数。 风-光-水-火联合系统综合成本可用式 (1)表示。
式中:F 为联合系统综合成本, 元;T 为调度周期,h;t 为调度时段, 个;NG、NW、NPV分别为火电、风电和光伏发电的装机容量,MW;ui,t表示第i 台火电机组在t 时段的启停状态,运行时其值为1,停机时其值为0;f(PG,i,t)为第i 台火电机组在t 时段的燃料成本, 元;Si,t为第i 台火电机组在t 时段的启动成本,元;CW和CPV分别为弃风惩罚成本系数和弃光惩罚成本系数, 取值均为1 000 元/MW;Pf,ω,j,t和PW,j,t分别为第j 个风电场在t 时段的预测出力和实际输出功率,MW;Pf,pv,k,t和PPV,k,t分别为第k 个光伏电站在t 时段的预测出力和实际输出功率,MW。
火电机组的燃料为煤,其成本f(PG,i,t)用式(2)计算。
式中:ai、bi、ci均为第i 台火电机组的发电成本系数。
1.2 约束条件
风-光-水-火联合系统的约束条件考虑电网功率平衡和各发电主体实际物理限制。
1.2.1 功率平衡约束
在任何时刻, 风-光-水-火联合系统的功率输入和输出都要保持平衡,可表示为式(3)。
式中:NH为水电站的数量,座;PH,n,t为第n 座水电站在t 时段的输出功率,MW;Pload,t为t 时段的系统负荷需求,MW。 其他符号同前。
1.2.2 机组出力约束
机组出力约束可表示为式(4)~式(7)。

式中:un,t表示第n 座水电站在t 时段的启停状态,运行时其值为1,停机时其值为0;kd为备用率,取值为0.02;mW为风电场备用容量系数,取值为0.15;nPV为光伏电站备用容量系数,取值为0.05。
2 改进磷虾群算法
2.1 磷虾群算法
磷虾群(krill herd,简称KH)算法是Gandomi等人根据磷虾群的觅食行为提出的一种智能优化算法[9]。 KH 算法的迭代寻优主要是通过邻近个体吸引、觅食行为和随机扩散3 个过程实现的。
在n 维空间中,KH 算法的拉格朗日数学模型可表示为式(13)。
式中:xi为第i 只磷虾的位置;τ 为迭代次数,次;Ni为邻近个体吸引的影响程度;Fi为觅食行为的影响程度;di为随机扩散的影响程度。
其中,Ni、Fi和di可根据式(14)~式(16)计算。

磷虾在区间 [τ,τ+Δτ] 的位置更新公式为式(17)和式(18)。

2.2 KH 算法改进策略
与传统寻优算法相比,KH 算法原理更简单,操作更方便,但在寻优过程中也容易陷入局部极值[10]。为了提高KH 算法的优化性能,本文采用Logistic 混沌映射、余弦控制因子、柯西变异3 种策略对KH 算法进行改进。
2.2.1 Logistic 混沌映射
在KH 算法中,磷虾初始种群是随机产生的。这样,无法保证磷虾个体遍布整个搜索区域中,从而限制了算法的全局搜索性能。 为此,采用Logistic 混沌映射产生初始种群, 使磷虾个体能够遍布整个搜索区域,Logistic 混沌方程为式(19)[11]。
式中:xi(τ)为磷虾个体i 的当前位置;xi(τ+1)为磷虾个体i 在下一次迭代的位置;γ 为分支系数,取值为3.95。
2.2.2 余弦控制因子
KH 算法中的吸引权重ωn和觅食权重ωf均为固定值,这样不利于算法平衡全局搜索和局部搜索。本文利用余弦控制因子使ωn和ωf随迭代次数不断变化,使算法在迭代前期侧重全局搜索,在迭代后期重点进行局部搜索,具体如式(20)所示。
式中:ωmax、ωmin分别为吸引权重和觅食权重的上限值和下限值;R 为随机数,R∈(0,1)。
2.2.3 柯西变异
针对KH 算法易陷入局部极值的不足, 在磷虾位置更新过程中引入柯西变异,具体如式(21)和式(22)所示[12]。

2.3 仿真测试
为了验证改进KH 算法的全局搜索性能, 采用表1 中的2 个测试函数进行仿真测试, 并利用KH算法和粒子种群优化(Particle Swarm Optimization,简称PSO)算法进行对比验证[13]。

表1 测试函数Tab.1 Test function
设置2 个测试函数的空间维度均为30, 改进KH 算法、KH 算法和PSO 算法的种群容量均为30,最大迭代次数均为500。利用3 种优化算法分别对2个测试函数进行20 次寻优,其平均收敛曲线如图1所示。
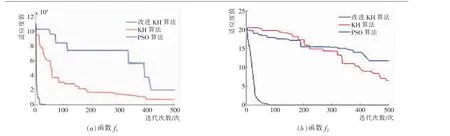
图1 三种算法的平均收敛曲线Fig.1 Average convergence curves of three algorithms
对比图1 可知, 与KH 算法和PSO 算法相比,改进KH 算法收敛时的迭代次数更少, 收敛精度更高。 这验证了Logistic 混沌映射、余弦控制因子和柯西变异3 种策略对KH 算法改进的有效性。
3 模型求解与验证
3.1 改进KH 算法求解联合系统优化调度模型
采用改进KH 算法对风-光-水-火联合系统优化调度模型进行求解,主要步骤如下:
(1) 设置联合系统调度周期及风电场、 光伏电站、水电站和火电机组的相关运行参数。
(2)设置改进KH 算法的相关参数,包括算法最大迭代次数、磷虾种群规模、吸引权重上下限、觅食权重的上下限。
(3)利用Logistic 混沌映射生成初始磷虾种群,将目标函数式(1)作为KH 算法的适应度函数,计算磷虾适应度值,记录磷虾群的最佳位置。
(4)执行迭代,磷虾群向食物中心位置靠拢,利用式(20)计算吸引权重和觅食权重。
(5)根据式(13)计算磷虾位置偏移量,更新磷虾位置并计算个体适应度值。
(6)对部分磷虾个体进行柯西变异,更新磷虾个体位置并计算适应度值。
(7) 判断算法最大迭代次数是否已经达到,若是,则输出最小综合成本;否则,返回步骤4。
3.2 模型验证
3.2.1 基本参数采用西南地区某风-光-水-火联合系统进行仿真分析。 该联合系统包括1 个风电场、1 个光伏电站、4 座梯级水电站和10 台火电机组, 其中,4 座梯级水电站运行参数如表2 所示,10 台火电机组的相关参数如表3 所示。
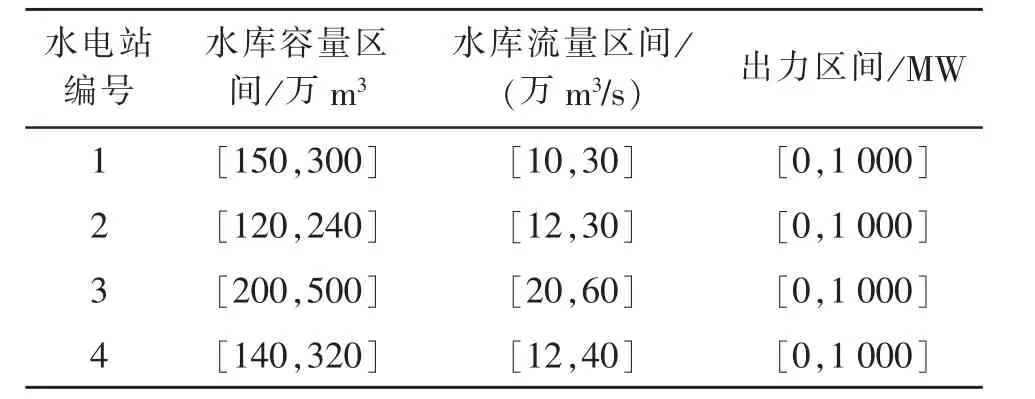
表2 4 座梯级水电站运行参数Tab.2 Operation parameters of four cascadehydropower stations

表3 10 台火电机组的相关参数Tab.3 Relevant parameters of ten thermal power units
设置调度周期为24 h。 以某夏季典型日为调度对象, 调度日当天风光出力及系统负荷需求情况如图2 所示。
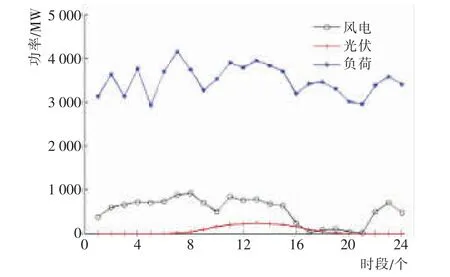
图2 调度日当天风光出力及系统负荷需求曲线Fig.2 Curves of wind-light power output and system load demand of scheduling day
3.2.2 仿真结果分析
在Matlab2019 软件中进行仿真分析。 分别采用改进KH 算法、KH 算法和PSO 算法对风-光-水-火联合系统优化调度模型进行求解,得出联合系统最小运行成本的收敛曲线,如图3 所示。 由图3 可以看出,改进KH 算法收敛至最小综合成本时迭代次数更少,所求最小综合成本低于KH 算法和PSO 算法。

图3 收敛曲线对比Fig.3 Comparison of convergence curves
改进KH 算法、KH 算法和PSO 算法的优化效果对比情况如表4 所示。 从表4 可以看出,在对风-光-水-火联合系统优化调度模型求解时, 改进KH算法经过52 次迭代后已收敛, 收敛时间为6.75 s,所求联合系统最小综合成本为109.01 万元,其在迭代次数、 收敛时间和求解精度方面均优于KH 算法和PSO 算法。 这验证了改进KH 算法在风-光-水-火联合系统优化调度模型求解方面的优越性。
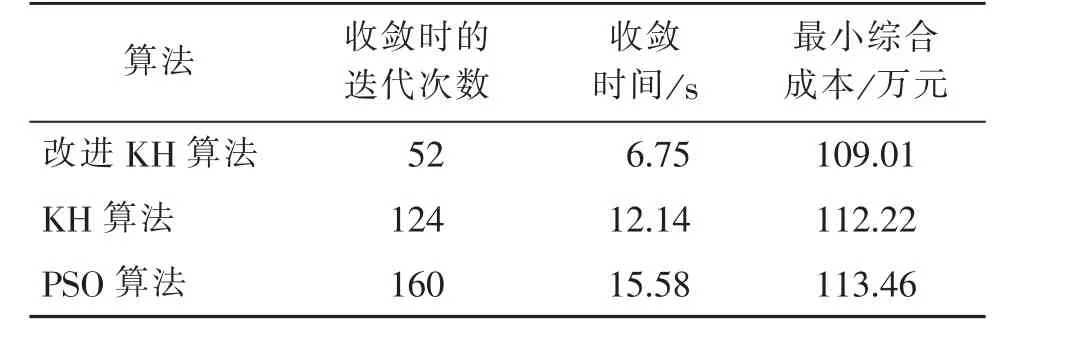
表4 三种算法优化结果对比Tab.4
图4 为改进KH 算法对风-光-水-火联合系统优化调度模型求解时各类电源的出力情况。 由图4可知,夜晚(1~6 时段、22~24 时段),风电出力相对充足,系统优先利用风电,减少火电出力;白天(7~17 时段)风光出力相对较大,系统优先利用清洁能源,其余负荷由水电和火电进行补充;傍晚(18~21时段)风电、光伏出力不足,系统负荷主要由水电和火电提供。 在此调度策略下,风-光-水-火联合系统在满足系统供需平衡的同时,优先利用风电、太阳能等清洁能源,既提高了清洁能源利用率,又减少了对环境的污染。
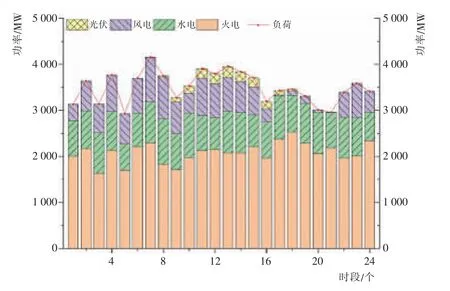
图4 各类电源出力情况Fig.4 Optimization results comparison of three algorithms
4 结语
本文以风-光-水-火联合系统综合成本最小为目标函数,综合考虑各种约束条件,建立了风-光-水-火联合系统优化调度模型。 利用Logistic 混沌映射、余弦控制因子和柯西变异等3 种策略对KH 算法进行改进,提高了改进KH 算法的全局搜索性能。 分别采用改进KH 算法、KH 算法和PSO 算法对某风-光-水-火联合系统优化调度模型求解, 得出改进KH 算法在迭代次数、收敛时间和求解精度方面均优于其他优化算法的结论, 同时也验证了所提风-光-水-火联合系统优化调度模型的实用性和优越性。

