考虑边坡渐进破坏特性的新型条分法及其应用

刘东泽，江俊杰，朱玉蕊

（ 1.中冶武勘工程技术有限公司，湖北 武汉 430080；2 湖北工业大学 土木建筑与环境学院，湖北 武汉 430068）

0 引言

自1915 年瑞典的彼得森提出圆弧滑动法开始，人们对边坡稳定性的研究从未停下脚步。 应用圆弧滑动法进行边坡稳定分析时， 没有考虑条块间的推力或只考虑条块间的水平推力， 故计算结果不能完全符合实际。瑞典费伦纽斯于1927 年又提出瑞典条分法。该方法计算忽略了土条间的作用力，所以不满足静力平衡条件。但由于其计算结果偏于安全，在工程上仍有广泛的应用。在随后的几十年中，瑞典条分法不断改进，但仍然有较大的缺陷［1-2］。基于此，英国专家A.W.Bishop 又提出一种更为精确的计算方法，即简化Bishop 法［3］，它也是我国规范中的主要计算方法，但后来人们在工程实际中发现，许多滑坡并不是沿着圆弧面滑动的。于是，又针对此类滑坡提出简布法与强度折减法等［4］。

传统的条分法大多是基于极限平衡法计算， 主要通过最小安全系数来反映边坡的稳定情况。随着研究的深入，诸多学者都认为边坡是一个渐进破坏过程［5-7］，传统条分法并不能反映出其渐进过程，对边坡的稳定性分析也过于单一，所以建立一种可以反映边坡渐进破坏的条分法尤为重要。笔者通过引入一种剪应力—应变本构模型，对条分法进行改进，以期反映出边坡的渐进破坏过程，为边坡的监测预警提供参考。

1 基于剪应力—应变本构模型的条分法

1.1 剪应力—应变本构模型

在传统的条分法计算中， 往往需要通过多种假定才能完成计算。对于岩土体的变形关系，大多是基于理想弹塑性模型进行分析。但是，理想弹塑性模型有一个明显的缺陷，就是当岩土体应力达到峰值后，应力趋于平衡，不再随着应变而变化。而在大量的工程实践中，岩土体表现出软化特性，并不满足这一条件。 基于此， 本文引入一种剪应力—应变本构模型（如图1 所示），分析岩土体应力与应变的关系。从图1 可以看出，在应力达到临界状态后，材料会出现软化现象。 这与实际土体性质更为接近。

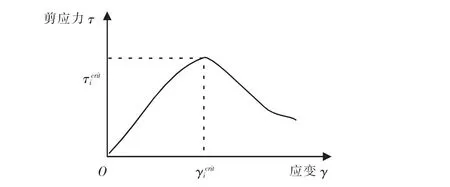
图1 剪应力—应变本构模型Fig.1 Shear stress-strain intrinsic structure model

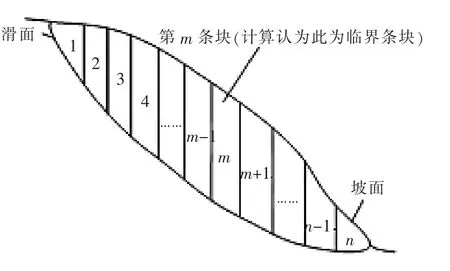
图2 边坡稳定分析条块划分图Fig.2 Block division diagram of slope stability analysis

剪应力—应变本构模型的表达式为式（1）。

式中：τ 为剪应力，kPa；γ 为剪应变；G 为岩土体的剪切模量，kPa；p、q、ξ 为常系数。

当土体应力达到峰值后，式（1）满足式（2）所示条件。

式中：γpeak为峰值应力状态下的应变。

计算时， 认为临界状态的应变仅与法向应力有关，如式（3）所示。

式中：σn为法向应力，Pa；a01、a02、a03为常系数。

对于式（1）中无量纲参数ξ，结合土壤水分特征曲线可以用式（4）计算。

通过多次法向压力试验便可计算出此方程。

1.2 新型条分法

通过引入剪应力—应变本构模型， 可以克服传统条分法的一些缺点。 新型条分法通过监测变形情况来反映边坡状态， 而不像传统计算方法仅仅靠折减系数来模拟边坡的破坏过程。以剩余推力法为例，对于整个边坡中任一条块正压力可表示为式（5），则其对应的正应力为式（6）。引入剪应力—应变本构模型后，摩阻应力表示为式（7），临界状态下的摩阻应力表示为式（8）。

式中：Ni为第i 条块正压力，kN；Wi为第i 条块重量，kN；βi为地表竖向均布荷载，kN／m；Δi为水平方向均布荷载，kN／m；li为条块底边长度，m；αi为条块底边与水平夹角，（°）。

式中：τi为第i 条块的剪应力，kPa；γi为第i 条块的剪应变；Gi为剪切模量，kPa。

式中：ci为第i 条块的黏聚力，kPa；ϕ 为内摩擦角，（°）。

摩阻力计算式为式 （9）， 下滑力计算式为式（10），驱动剪应力计算式为式（11），剩余下滑力计算式为式（12）。

在剪应力—应变本构模型中， 在应力达到峰值后，条块会出现软化行为，所以在破坏后区，条块的摩阻应力应小于临界摩阻应力。 对于临界状态之前的条块，其条块正压力与正应力计算仍按上式计算，但达到临界状态时，其对应的剪应变应采用式（13）计算。临界摩阻应力按摩尔库伦准则计算，如式（14）所示。

对于破坏后区的剪应变计算，假设第m 条块处于临界状态，对于第m＋1～n 条块剪应力状态，按剪应力—应变本构模型计算，如式（15）所示。

第m 条块峰值剪应变按式（13）确定，第1～m-1条块剪应变以峰值剪应变逆推，如式（16）所示。

通过计算， 可以得出所有条块的剪应力τiX、下滑应力τiu、法向应力σi，nX。

2 新型条分法渐进破坏多参量稳定分析

按剪应力—应变本构模型条分法计算后， 建立滑体稳定性评价指标。

2.1 综合下滑力—抗滑力法稳定系数（FCSRM）

首先用式（17）、式（18）和式（19）计算任一条块现状驱动下滑力在水平方向、 竖直方向的分量及综合矢量和。

对于综合矢量和PS与水平轴形成的最小夹角αs可采用式（20）计算。

抗滑力为沿滑面每一条块破坏状态的摩阻力和正压力在水平方向、 竖直方向的分量及综合矢量和的计算式为式（21）～式（23）。

综合矢量和与水平轴形成的最小夹角应用式（24）计算。 水平方向、竖直方向、沿着下滑力方向的稳定系数分别采用式（25）、式（26）、式（27）计算。

2.2 主推力法稳定系数（FMTM）

对于第1 条块至临界状态条块（第m 条块），沿滑面每一单元的剩余下滑力Pi在水平方向和竖直方向矢量和Pxm和Pym采用式（28）和式（29）计算，综合矢量和Pm的计算式为式（30），Pi综合矢量和与水平轴形成的最小夹角αm采用式（31）计算。

对于第m＋1 条块至第n 条块，沿滑面破坏时的摩阻应力τip，b与现状摩阻应力之τiX差在水平方向、竖直方向的分量及综合矢量和分别用式 （32）、式（33）、式（34）计算。其综合矢量和与水平轴形成的最小夹角αfm采用式（35）计算。 水平方向、竖直方向、沿主下滑力方向的主推力稳定系数分别采用式（36）、式（37）、式（38）计算。

2.3 综合位移法稳定系数（FCDM）

应用式（39）～式（41）求解每一条块现状剪应变在水平方向、竖直方向的分量及综合矢量和。

综合矢量和Ss与水平轴形成的最小夹角αss的计算式为式（42）。

破坏时，沿滑面每一条块的位移在水平方向、竖直方向的分量及其综合矢量和分别用式 （43）、式（44）和式（45）计算。

综合矢量和S 与水平轴形成的最小夹角αscrit采用式（46）计算。

位移在水平方向、 竖直方向和沿位移下滑方向的稳定系数分别用式（47）、式（48）、式（49）计算。

2.4 富余位移法稳定系数（FSDM）

富余位移法稳定系数的定义类似于力的富余稳定系数， 对于选定的滑体， 在第1～n 条块范围内， 计算破坏沿滑面每一单元的位移Si， 并用式（50）和式（51）计算其在水平方向和竖直方向矢量和Smx和Smy，再用式（52）求位移综合矢量和Sm。 综合矢量和Sm与水平轴形成的最小夹角αmss采用式（53）计算。

同理，在第m＋1～n 条块范围内，当滑体沿潜在滑面发生整体破坏时， 计算此时沿滑面可能发生破坏的每一条块的临界位移Scriti与现状位移Si之差，分别采用式（54）、式（55）计算其在水平方向、竖直方向的位移矢量和Scrit-tx、Scrit-ty，再采用式（56）计算其综合矢量和Scrit-t， 综合矢量与水平轴形成的最小夹角αs-tcrit-t采用式（57）计算。

在水平方向、 竖直方向位移稳定富余系数采用式（58）和式（59）计算。 沿位移主滑方向富余系数采用式（60）计算。

3 实例分析

3.1 计算模型

以西北地区的一个实际边坡为例，进行计算。该边坡呈多级分布，主要由沙质黄土、粉土及风化泥岩组成，容重为18.3 kN／m3，滑床为泥岩夹沙岩，滑动面位于岩土交接面附近的泥岩风化层及破碎带中。选取该边坡主断面Ⅱ-Ⅱ′断面作为计算断面， 其条块划分如图3 所示。

图3 滑坡Ⅱ-Ⅱ′剖面条块划分图Fig.3 Block division diagram of landslide II-II′ profile

根据现场勘察及实验分析， 确定模型的计算参数（如表1 所示）。

表1 滑坡计算取值表Tab.1 Values of landslide calculations

3.2 计算结果分析

利用传统的部分强度折减法， 计算出边坡的稳定系数为1.765。图4 为部分强度折减稳定系数与临界条块号（CSN）的关系曲线。在分析时，认为稳定系数等于1 时的条块为临界条块。由图4 可知，传统算法中临界状态条块为第14 号条块，随着临界条块的推移，部分强度折减稳定系数逐渐增大。图5 为富余稳定系数图。由图5 可以看出，边坡的稳定系数在逐步减小。

图4 部分强度折减稳定系数Fig.4 Stability coefficients of partial strength discounting

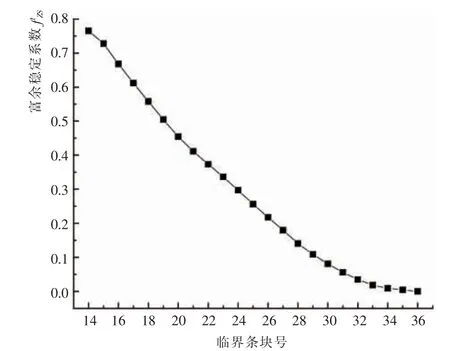
图5 部分强度折减法的富余稳定系数Fig.5 Surplus stability coefficients of partial strength discounting method

对于基于剪应力—应变本构模型（CPCM）改进的条分法，边坡的初始临界条块为第15 块，随着临界条块的推移，边坡受力也在发生变化。 图6～图8为临界位置在典型条块时边坡的下滑力、 摩阻力以及剩余下滑力的变化曲线。由它们可以看出，随着临界条块的推移，最大下滑力、摩阻力以及剩余下滑力在不断后移。 临界条块为16 块时，最大的下滑力出现在第7 条块， 而摩阻力最大值出现在第13 条块。在临界条块移动至最后一块时， 最大的下滑力出现在第13 条块，而摩阻力最大值出现在第11 条块。这也说明，边坡在临界位置推移的过程中，条块间的受力也在不断变化。

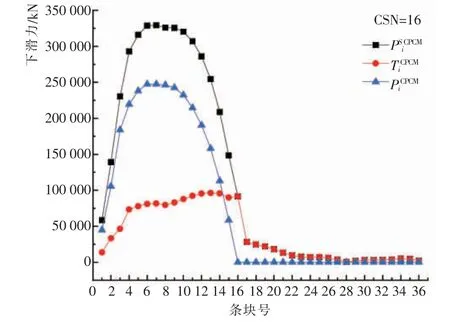
图6 临界条块为16 块时的各条块受力情况Fig.6 Force on each block of 16 critical blocks

图7 临界条块为26 块时各条块受力Fig.7 Force on each block of 26 critical blocks

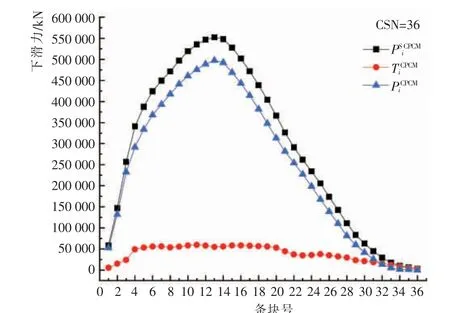
图8 临界条块为36 块时各条块受力Fig.8 Force on each block of 36 critical blocks

为进一步分析边坡稳定性的变化， 计算边坡随着临界条块变化的4 种稳定系数（FCRSM、FMTM、FCDM、FSDM），其变化曲线如图9～图12 所示。

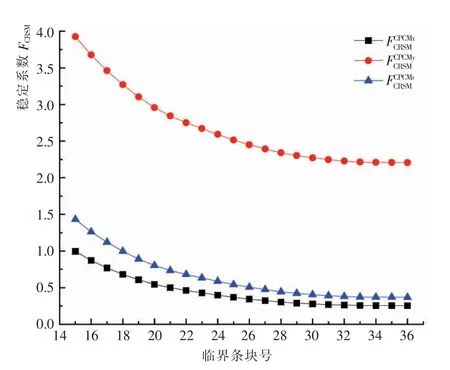
图9 FCRSM 随临界条块的变化情况Fig.9 FCRSM changes of different critical blocks

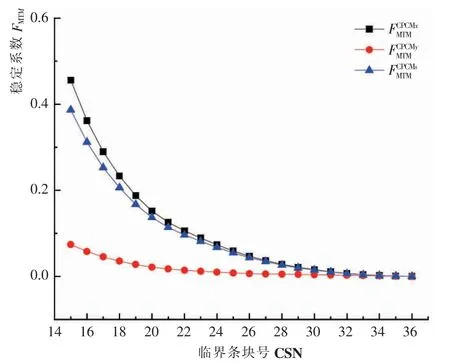
图10 FMTM 随临界条块的变化情况Fig.10 FMTM changes of different critical blocks

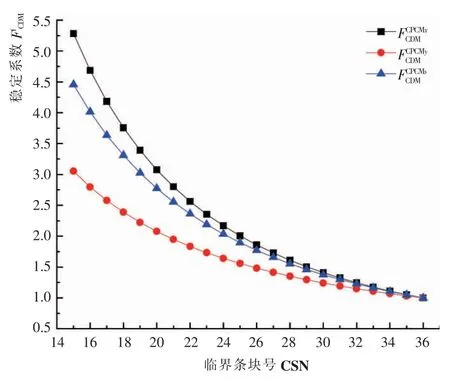
图11 FCDM 随临界条块的变化情况Fig.11 FCDM changes of different critical blocks

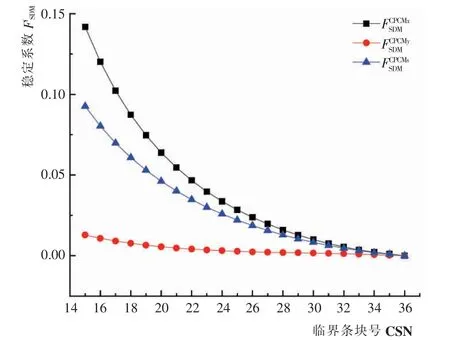
图12 FSDM 随临界条块的变化情况Fig.12 FSDM changes of different critical blocks

在滑坡临界状态条块从第15 块演变到第36 块的过程中，综合下滑力—抗滑力法稳定系数、推力法稳定系数和富余位移法稳定系数减小， 综合位移法稳定系数逐渐减小，并趋于1。 主推力法稳定系数可以反映出滑体整体力的富余程度， 富余位移法稳定系数则表示位移的富余程度， 而综合下滑力—抗滑力、 综合位移法分别表示边坡随位移变化时整体力和位移的演化规律。在变形曲线中也可以看出，在临界条块到达第36 块时， 边坡已经失去抗滑能力，进入整体破坏阶段。

从渐进破坏稳定性评价指标的变化趋势来看，尽管目前边坡前部仍未破坏， 但在上部岩土体和外部不确定因素的作用下，随时都有发生破坏的可能，即边坡随时可能发生整体破坏，情况十分危险。对于边坡的破坏机制可归结为： 先发生破坏的部分岩土体使边坡后缘发生受拉破坏且向下滑动。 随后临界位置开始移动， 边坡的下滑力和剩余下滑力开始向破坏状态逐步增大，破坏区摩阻力出现软化现象。随着临界状态达到最后一块时，边坡稳定系数趋于0，整个滑动面贯通，边坡处于整体破坏状态。

3.3 监测对比

基于剪应力—应变本构模型的条块分析法计算所得的初始临界状态条块为第15 条块，此时1 号检测仪所在位置的理论位移值为76.826 mm （这是相对于未破坏时的位移值）。1 号检测仪起始监测时间为2016 年9 月10 日，监测位移值为0 mm。因此，不同临界状态下1 号检测仪所在位置的理论位移值相对于其初始临界状态下的位移变化量， 即为计算位移值。 将1 号检测仪的监测位移值与计算位移值进行比较，结果如图13 所示。 2 号与3 号检测仪所对应临界条块处于第15 条块与第16 条块， 同理得出其对应的对比关系图如图14 和图15 所示。 对于后续安装的4 号检测仪， 在剪应力—应变本构模型计算过程中对应的临界条块为第20 条块，其监测位移值与计算位移值的对比关系如图16 所示。

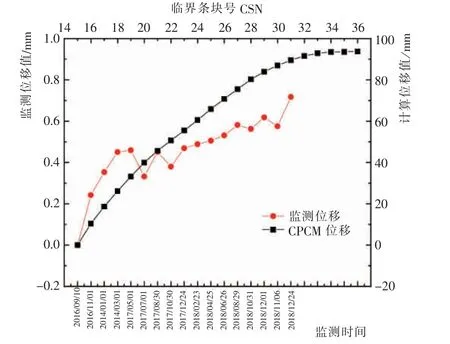
图13 1 号检测仪监测位移与计算位移对比图Fig.13 Comparison of monitored and calculated displacements of No.1 detector

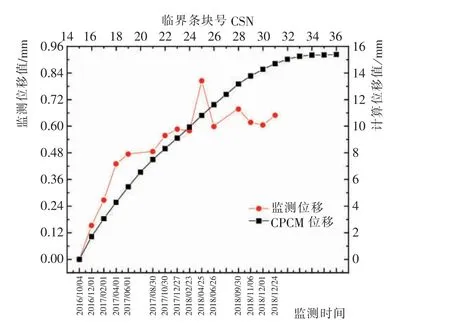
图14 2 号检测仪监测位移与计算位移对比图Fig.14 Comparison of monitored and calculated displacements of No.2 detector

图15 3 号检测仪监测位移与计算位移对比图Fig.15 Comparison of monitored and calculated displacements of No.3 detector

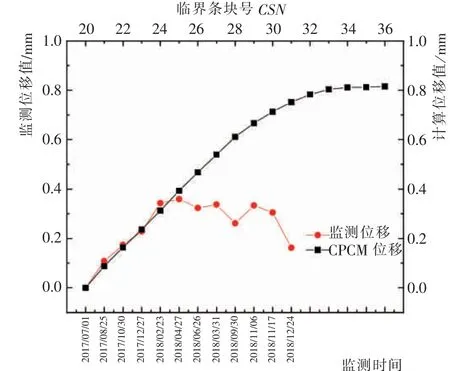
图16 4 号检测仪监测位移与计算位移对比图Fig.16 Comparison of monitored and calculated displacements of No.4 detector

通过对比监测位移值与计算位移值可以看出，改进后的条分法计算结果与现场边坡的实际变化基本一致，而且从4 号监测对比曲线可以发现，引入剪应力—应变本构模型后， 边坡早期的微小变形也可以通过计算模拟出来。 这也反映出改进后的计算方法完全可以应用于实际工程中， 为边坡变形预警提供参考。

4 结语

本研究将剪应力—应变本构模型引入至条分法中， 利用改进的条分法可以对边坡渐进破坏进行全过程描述，揭示边坡不同阶段的受力情况。本文提出的4 种边坡稳定性评价指标可以演化描述边坡渐进破坏过程中各参量的物理力学指标。 将基于全过程的剪应力—应变本构模型与条块分析法的多参量时空稳定性评价指标结合起来， 可较好地描述边坡渐进破坏过程中力和位移的变化特征， 也可较好地评价边坡的稳定性。 改进后的条分法将力和变形联系起来，比仅仅分析受力的传统条分法更为科学合理。