基于电动汽车数量预测的充电站规划研究

■李梓豪

（国网山西省电力公司电力科学研究院, 山西 太原 030001）

随着经济发展与“碳达峰、碳综合”目标的提出，电动汽车数量也随之快速增加，但电池技术的缺乏和充电基础设备建设数量不足制约了电动汽车的有效推广，如何对大量新增的充电服务设施经济合理规划也成为当前急需解决的问题。针对电动汽车保有量预测，研究学者大多采用离散模型、多代理模型及创新扩散模型这三种模型进行建模。离散选择模型和多代理模型均着眼于消费者个体，而创新扩散模型从宏观视角对电动汽车的市场化进行建模，主要包括Logistic 模型、Bass 模型和Gompertz 模型等[1]。针对充电站规划研究，张程嘉[2]采用Voronoi 图对充电站服务区域进行划分并计算充电站服务半径，以各充电站服务半径最大确定选址方案。赵书强[3]基于集覆盖理论提出了在满足一定约束条件下使充电站数量最少的选址模型。葛少云[4]利用加权Voronoi 图划分充电站的服务范围，以服务分区内用户每年在充电路程中的损耗成本和充电站线路年投资之和最小为目标来进行站址选择。

本文所提出充电站规划方法，通过对充电站位置、数量做出优化，降低充电站建设成本及用户充电成本，提高充电站服务质量，为充电站规划和建设提供一种新的思路。本文就电动汽车数量预测和充电站规划求解方法展开讨论，并以S 地区市为实际算例，在预测S 地区市某区域电动汽车保有量基础上对该区域充电站规划建设进行仿真。

一、电动汽车保有量预测

电动汽车保有量预测存在着历史市场统计数据缺乏、变化幅度大的难题，能够准确预测城市区域电动汽车保有量和电动汽车充电负荷分布是对电动汽车充电站科学合理规划的前提和基础。本文首先通过Eviews 软件根据时间序列分析理论对S 地区市汽车市场进行建模预测，然后基于预测数据采用Bass 模型建立山西省电动汽车保有量预测模型，最后根据S 地区市电动汽车数量预测结果，对不同情景下电动汽车充电设施建设规模进行分析。

（一）时间序列分析模型

时间序列分析是指将原数据分解为四部分内容，分别为趋势、周期、时期和不稳定因素，然后综合这些因素，对原有数据进行回归预测的过程，是一种非常重要的定量分析方法[5]。本文建立时间序列分析模型如图1所示。

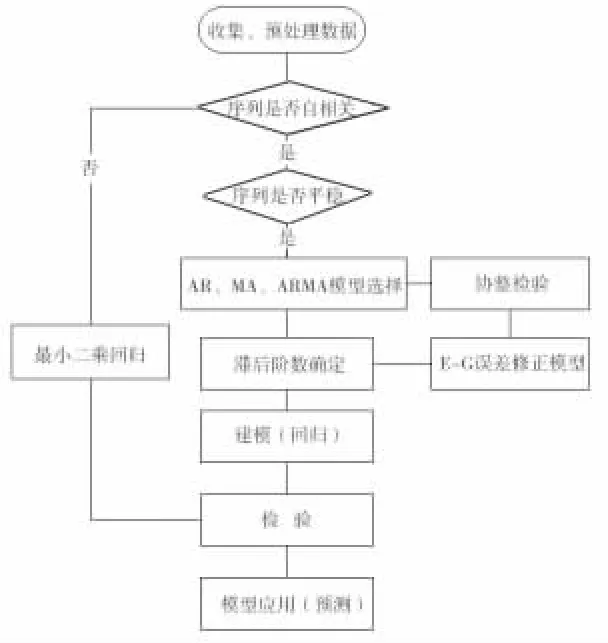
图1 时间序列分析流程

（二）BASS 模型

BASS 模型是一个基本创新扩散模型[6]，其数学公式如式（1）所示：

（三）地区市汽车保有量预测

根据时间序列分析理论、Bass 模型，通过Eviews 软件对未来五年电动汽车数量进行预测。首先通过Eviews软件对2016—2019 年末S 地区市汽车保有量序列进行自相关检验，用ADF 检验方法对2016—2019 年原始数据进行平稳性检验[7]。经过检验可以判断原始数据经过一阶差分后为含截距项平稳数据，即S 地区市年电动汽车保有量增长个数为含截距项平稳数据。

然后根据Bass 模型通过Eviews 软件预测中国电动汽车的保有量[8]，其表现形式为：

其中，f (t+1) 表示在t+1年中新增消费者数量占t+1年潜在消费者的比例，F（t）表示在t 累计时间内潜在客户中已购买电动车消费者比例，每个时间段内电动汽车购买的数量等于f（t）乘以潜在消费者数量m。通过对三个输入变量p、q、m 系数确定，可以预测电动汽车每年消费者持有比例。其中，p 为内部影响系数（创新系数），取值0.35，q 为外部影响系数（模仿系数），取值0.02，m 为最大市场潜力，取值90%。

由于S 地区市在2016 年间大规模引入电动出租车替换传统燃油出租车，这里选择2016 年作为起始年份，根据电动汽车最大市场潜力为90%，结合对S 地区市汽车保有量预测结果计算年末电动汽车潜在数量及最大市场潜力[9]，根据计算结果如表1 所示。

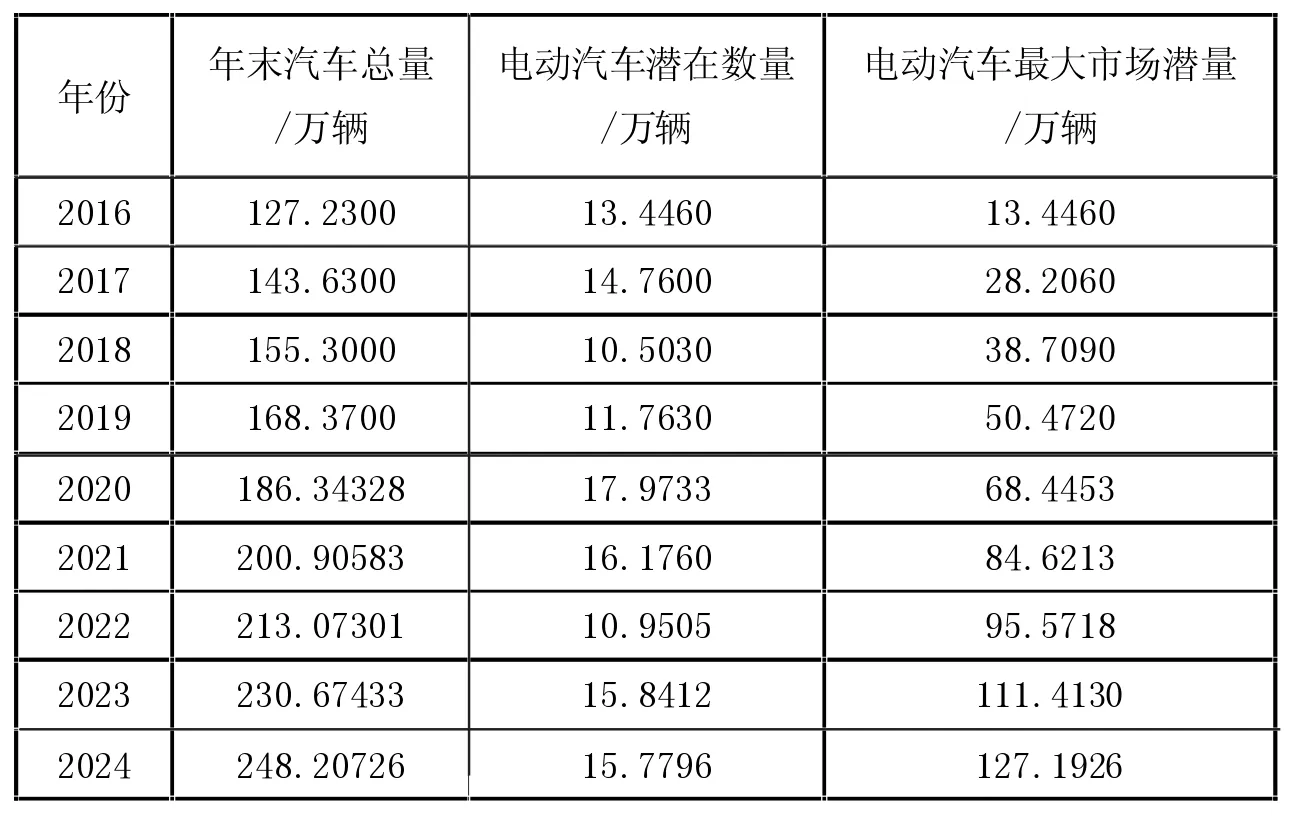
表1 S 地区年末电动汽车潜在数量及最大市场潜力

数据显示，S 地区市电动汽车2019 年底保有量为36871 辆，根据电动汽车潜在数量及市场最大潜量，通过Bass 模型公式，得到f（t）和F（t）结果如表2 所示。

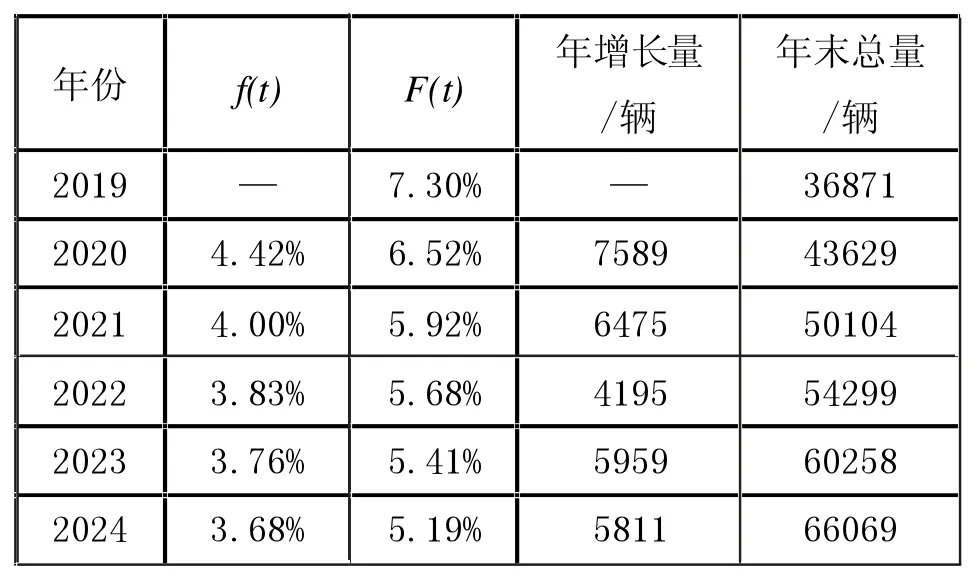
表2 S 地区电动汽车年增长量与年末总量

由表2 可知，通过Bass 模型预测电动汽车结果2020 年为43629 辆，而S 地区市公信厅数据显示2020年末电动汽车保有量为47643 辆。预测值同实际值较为接近，表明预测结果真实可信。

二、充电站规划模型

规划区新建设充电站容量同未来区域电动汽车数量相关，而充电站位置则与规划区电动汽车分布有关。本文在对S 地区市电动汽车数量预测的基础上，进一步对规划区域电动汽车及各子区域电动汽车数量做出预测。同时考虑充电站建设运行成本及用户充电途中成本，建立区域充电站规划模型，使得最终的规划区域全社会综合年总成本最小。

（一）区域电动汽车保有量预测模型

区域用电负荷水平可以同时反应当地人口数量、人民的生活水平和社会意识水平等状况。在某种程度上，某一地区电动汽车保有量和该地区电力负荷具有某种相关性关系，因而，某地区用电力负荷可以作为该地区电动汽车保有量预测的一个关键因素[10]。根据区域用电负荷和地区用电负荷数据，S 地区某区域电动汽车保有量可以表示为：

式中，nev,j为j 区域电动汽车数量；fc(·)为向上取整函数；hj为j 地区人口数量；Pj为j 地区电力负荷；Psum为S 地区地区总用电负荷；nev,sum为S 地区地区电动汽车总数量。

（二）基于成本的充电站选址模型

电动汽车充电站的成本主要包括用地成本、建站成本、运营成本以及用户充电途中年耗时成本。其中充电站的占地面积和具体位置是用地成本的重要影响因素，建站成本与充电站数量和基础设施有关，运营成本与人员工资、维护成本、充电桩个数以及运营时间等有关，用户充电途中年耗时成本同城市出行时间成本、充电需求点到充电站距离、城市交通平均行驶速度有关[11]。

1.用地成本

在建设充电站时，土地资源成本占有很大部分比重。不同的区域土地价格也不同，所以应该求解出不同建站地点的土地价格。根据《城镇土地估价规程（GB/T185058-2014）》, 单位面积用地成本Clqi公式如式（7）所示：

其中：Ci和Si分别是节点i 处单位面积成本和建立在i 点处的充电站占地面积。

2.充电站建设成本和运营成本

充电站建设成本包括充电站内充电桩成本、基建成本以及各配到设施的成本。充电站运营成本主要指人员工资、日常维护费用以及配套设施的损耗费用等，一般与建设成本成正比。

3.用户充电途中年耗时成本[12]

充电途中年耗时成本是指用户赶往距离最近的充电站途中所消耗的时间及电动汽车电量折算到经济性后的具体费用。

（三）充电站规划目标函数与约束条件

本文所建立模型决策变量为各电动汽车充电站充电桩数量，并且设定充电站充电桩数量为大于等于零的整数，当充电桩数量大于零时表示在该站点建设充电站，当充电桩数量等于零时表示不在该站点建设充电站[13]。模型以规划年平均社会总成本为目标函数，包括充电站的建设费用、充电站的年运行费用和电动汽车充电过程中产生的年时间成本[14]。具体目标函数如下：

式中，F 为折算后的社会年总成本；Cinv为充电站的年建设成本，；Crun为充电站的年运行成本；Ccost为电动汽车充电过程中产生的年时间成本。

1.充电站的年建设成本

式中，r0为贴现率；m 为折旧年限；I 为备用充电站点集合数；Nchi为充电站i 内充电机的数量；Csta为每新建一座充电站产生的固定成本；q 为单台充电机的价格；e为与充电机数量有关的等效投资系数，包括占地面积、配电变压器容量和电缆等。

2.充电站的年运行成本

式中，Chum为每一座充电站的人工成本；Cman为单台充电机年维护成本。

3.电动汽车充电过程中产生的年时间成本

式中，α 为充电过程行驶成本系数；β 为城市出行时间成本系数; Ji为充电站i 服务范围内充电需求点集合；nj为需求点j 电动汽车数量；v 为电动汽车平均行驶速度；dij为需求点j 到充电站i 的距离。

约束条件主要考虑了充电排队时间约束、充电桩数量约束、功率约束[15]。具体约束条件如下。

（1）各充电站排队时间约束

式中，Wi为充电站i 车辆排队等待时间期望，Wi大小由排队论模型确定。根据排队论的M/M/s 模型，电动汽车排队等候时间期望Wi为：

式中，ρi为充电站i 充电机服务强度，Pzi为充电站i充电机全部空闲的概率，λi为服从泊松流的单位时间内到达充电站i 的电动汽车数量，μ 为充电机的平均服务速率，nevi为充电站i 服务范围内电动汽车数量，tc为电动汽车充电时段，ts为充电机单车充电时间。

（2）充电桩数量约束

式中，Nmax为每个充电站充电桩数量上限。

（3）功率约束

式中，Pch为充电桩单机充电功率，总充电机功率满足充电负荷需求，Pmin为区域内最小充电功率。

（四）充电站规划模型

采用遗传算法和Voronoi 图联合求解的方法，建立充电站规划模型[16]，规划模型联合求解整体流程具体步骤如下。

（1）输入规划地区的基本数据：输入城市规划单位区域图形坐标及用电负荷，用式（4）计算各需求点电动汽车数量，输入备选电动汽车充电站图形坐标。

（2）置迭代次数Gen=1，产生初始群体即n 个备选充电站充电桩的数量Nchi=[Nch1，Nch2，Nch3，…，Nchi…，Nchn]。

（3）根据各充电站充电桩数量分配充电站坐标，若Nchi>0 表明在该点安装充电桩，分配对应备选站点图形坐标，若Nchi=0 表明不在该点安装充电桩，不分配对应备选站点图形坐标。

（4）根据充电站图形坐标作V 图，对各充电站服务区域进行划分并确定各充电站服务范围内电动汽车数量nevi，确定充电需求点到充电站距离dij。

（5）根据模型计算各染色体的适应度值，即充电站规划社会总成本，记录最优染色体Nchi和最优适应目标函数值F。

（6）对规划群体进行选择、交叉、变异操作，产生新个体。

（7）进行规划循环停止条件判断，若达到最大迭代次数或者最优适应度值变化率小于设定值，输出最优染色体Nchi和最优适应目标函数值F，否则置Gen=Gen+1返回步骤（3）。

三、S 地区地区实际算例分析

为了进一步验证充电站规划模型的有效性与通用性，对S 地区市某地区一个区域进行仿真分析，预测该地区五年后电动汽车数量及电动汽车负荷分布，并确定充电站建设最佳位置和充电站内配置的最优充电桩数量。

（一）区域介绍

选取S 地区市某地区一个区域如图2 所示，该地区包含了居民区、商业区、工业区和风景区，其中以居民区和商业区为主，在充电站规划建设时也更多考虑了面向私家车的充电站类型。该地区长3.8 km，宽3.3 km，面积为12.545 58 km2，分为31 个子区域，子区域充电需求点位置及序号在图2 已标明。

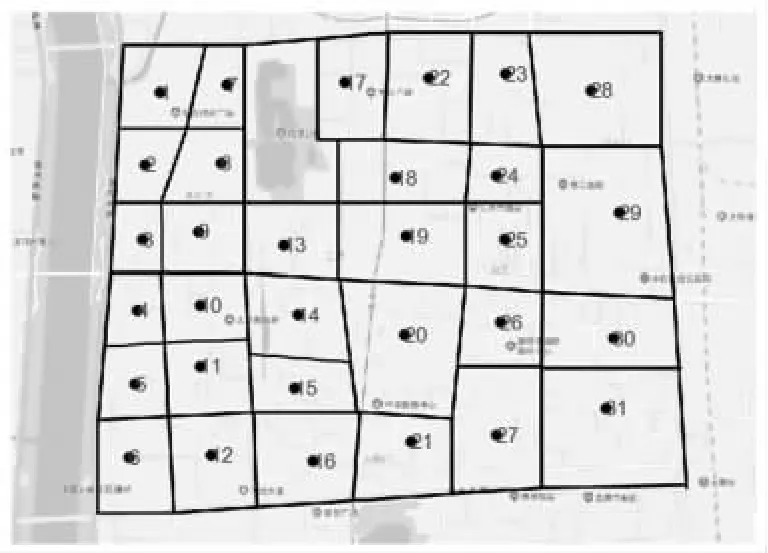
图2 规划区

（二）基于Bass 模型区域电动汽车数量预测

依照国家充电基础设施成长规划指导意见，S 地区市为新能源试点城市，综合考虑全市经济成长、产业结构、新型城镇化、交通结构等诸多因素，估计“十三五”时代，随着人民群众生活水平进步、电动汽车核心技术的快速成长和生态环境保护意识不断加强，全市电动汽车将迎来较大成长，电动汽车替换量将逐年上升，电动汽车逐步由以公务车为主过度为私家乘用车为主。根据S地区市公信厅数据显示，全市2019 年末电动汽车保有量为36871 辆，将地区市汽车保有量预测结果代入式（3）得到规划区电动汽车保有量预测结果如附表1 所示。

附表1 S 地区电动汽车数量预测结果

（三）仿真实验

假设用户在充电站充电为节省时间均选择快速充电方式进行充电，充电桩充电功率恒为60 kW，所有需要充电电动汽车电池容量均为40kW·h；电动汽车用户到达充电站服从泊松分布，暂不考虑当地土地价格差异因素。

S 地区地区民用日用电量为82990 MW·h，预测结果显示2024 年S 地区地区电动汽车总保有量为67227，各需求点图形坐标、电力负荷、各备选站点图形坐标如下表所示。贴现率r0为0.08，折旧年限m 为20 年，每新建一座充电站产生的固定成本Csta为100 万元，单台充电机的价格e 为10 万元/台，等效投资系数e 为3 万元/台，每一座充电站的人工成本Chum为4 万元/年，单台充电机年维护成本Cman为1 万元/年，充电过程行驶成本系数α 为25 元，电动汽车平均行驶速度v 为25 km/h，最大排队充电时间twait为0.25 h，电动汽车充电时段t_c 为48 h，充电机单车充电时间ts 为0.5 h，每个充电站充电桩数量上限Nmax为20 台，充电桩单机充电功率Pch为60 kW，区域内最小充电功率Pmin为1200 kW。图中各子区域充电需求点坐标、电力负荷如附表2、附表3 所示。

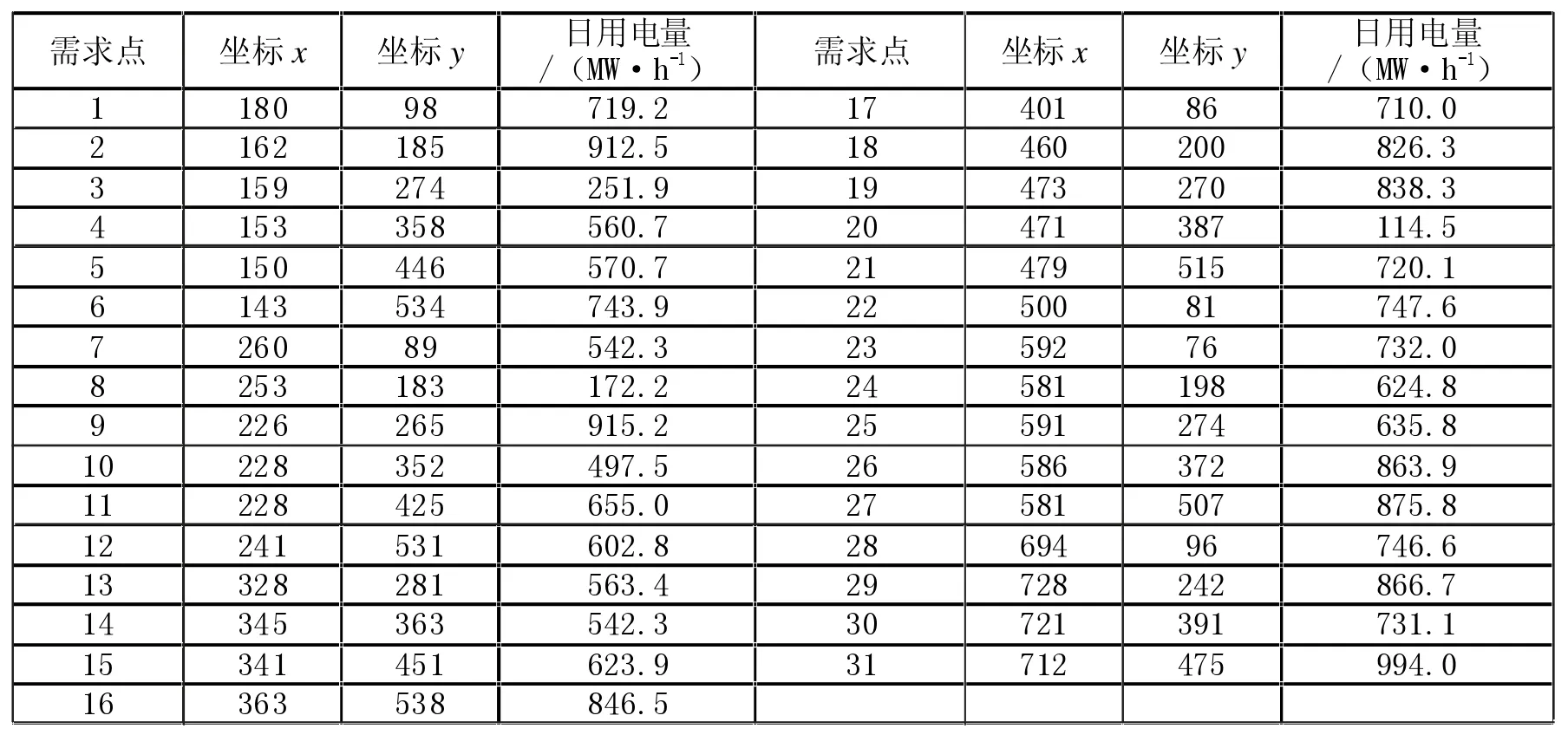
附表2 各需求点图形坐标及电力负荷表

附表3 各备选站图形坐标表

（四）仿真实验结果分析

根据上文所提出的选址模型及相应求解算法，计算出该区域规充电站最优规划建设充电站数量为6 座。每座充电站对应所需建设充电桩数量及各项成本如附表4所示：

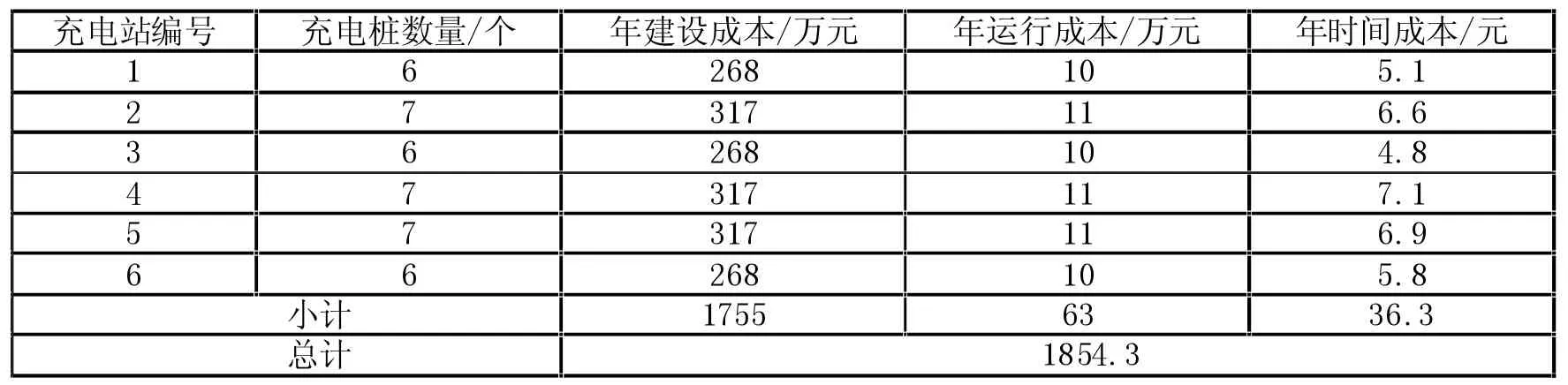
附表4 规划结果

在规划区中，V 图服务区划分及充电站建设位置规划结果如图3 所示：

图3 充电站建设规划结果

四、结论

结果表明，该模型能较好地预测未来几年电动汽车的数量和计算充电站的规模，经分析可得预测结果与实际规划建设情况有相似性，以此可以验证所提算法的准确性。同时，它还可以优化充电站的分布，使之更加平衡。因此，该模型有利于政府规划未来电动汽车的发展。