点的复合运动中任意相切型问题速度分析的一种特殊解法1)
占旺龙 * 方燕飞
*(深圳技术大学中德智能制造学院,广东深圳 518118)
†(华侨大学机电与自动化学院,福建厦门 361021)
理论力学是研究机械运动规律的科学,具有理论性强、学习难度大的特点。同时,理论力学也是工科类专业中量大面广的基础课程,是工科机械、土木和车辆等许多专业的重要技术基础课,是进一步学习后续相关专业课程的基础。以机械专业为例,理论力学的后续课程有材料力学和机械原理。在日常教学过程中发现,学生往往没有归纳总结和再复习已学习知识的习惯,造成学期结束,对本课程知识内容的认知是“课程知识点相互割裂,内容多且杂乱”。[1-2]。
在点的复合运动这一章中,欲求动点的绝对速度、牵连运动(平移时)的速度或牵连运动(转动时)的角速度,通常需要选择两个不同的参考系,即:定参考系和动参考系[3]。动点相对于定参考系的运动可以看成动点相对于动参考系运动(相对运动)和动参考系相对于定参考系运动(牵连运动)的叠加,从而可以把一个复杂运动分解成两个简单的运动来进行研究[4]。在实际例题讲解过程中,通常将问题分为3 种类型,即:相接型、相切型和相交型,如图1 所示[5]。相接型的典型特征是刚体1 的一端始终与刚体2 接触,此时选择刚体2 作为动系,刚体1 上与刚体2 接触点为动点;相切型的典型特征是刚体1 靠在刚体2 上,两运动刚体的边缘相切,此时选择刚体1为动系,刚体2 的轮心为动点;相交型的典型特征是两刚体独立运动,但有相交点,以相交点为动点,分别以刚体1 和刚体2 为动系,利用动点的绝对速度和绝对加速度相同,进行两次点的合成运动分析。
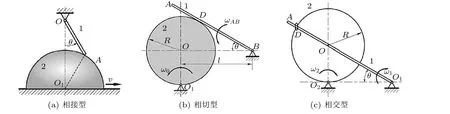
图1 点的复合运动中常见的3 类问题
相较于相切型问题,学生更容易理解相接型和相交型中动点和动系的选择过程。相切型问题的主要难点在于动点及动系的选择,教材中给出的例题都是利用圆心到圆周距离不变的特性进行分析,也就是说解决此类问题通常要求其中一个构件是圆形,而另一个构件的边缘必须足够简单。然而,在实际机构中,如图2 所示的平底从动件凸轮机构(凸轮作定轴转动),为了确保从动件的运动规律满足给定的速度和加速度要求,凸轮的轮廓可能不是圆形,而是任意可能的封闭曲线。在这种情况下,需要根据凸轮的外形及运动规律计算推杆的运动规律。根据点的速度合成定理,绝对速度va,相对速度vr和牵连速度ve之间满足

图2 平底从动件凸轮机构
在教材中通常会给出这样的说明:“若选择一个刚体上的切点为动点,另一个刚体为动系,由于相对运动轨迹为未知的平面曲线,导致相对运动速度的大小和方向亦难以确定,这样方程(1)中便含有3 个未知量,无法通过点的合成运动方法进行求解。”但若仅做瞬时速度分析,选择一个刚体上的切点为动点,另一个刚体为动系,速度分析依然可以完成。尽管相对运动轨迹未知,但是相对速度总是沿两个相切刚体轮廓线在切点的公切线方向上,从而式(1)亦仅有2 个未知量[6]。
传统分析方法既然无法求解,是否可以采用另外一种策略?问题根源在于相对运动轨迹未知,导致相对速度大小和方向都未知而无法求解,那么能否避开相对速度?即是否可以找到一个特殊的动点,在选择合适的动系后,使得相对速度vr=0 ,此时式(1)变为va=ve。如果该方法可行,则任意相切型问题的求解就转化为寻找这样一个特殊动点。
本文综合应用点的复合运动和刚体的平面运动分析方法,可以求解任意相切型模型的速度问题。课程讲授过程中让学生在学习新内容的同时复习前面章节的内容,达到培养学生注重课程知识体系的内在联系和知识互通的能力,改变日常学习“只见树木而不见森林”的现状,同时也为后续课程的学习打下基础。
1 特殊动点的存在性
在理论力学刚体的平面运动这一章节,欲求作平面运动刚体上任意一点速度,有基点法、速度投影法和速度瞬心法。如图3 所示,作平面运动的刚体,若角速度ω ̸=0 ,则在每一瞬间,运动的平面图形上均唯一存在绝对速度为零的点,此点即为速度瞬心(点P),此时平面图形上任意点B的速度大小为

图3 速度瞬心
将上述平面图形的运动问题进行扩展,如图4 所示,两个互相独立运动的平面图形,通过上述分析方法可以找到各自的速度瞬心O1和O2。平面图形上其他任意点的速度大小可以通过角速度ω与点到速度瞬心的距离的乘积得到,即
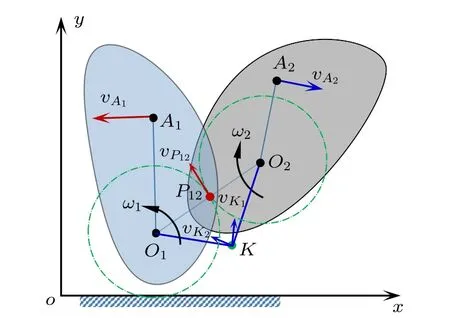
图4 两个作平面运动的图形分析
由此可得到如下推论:两个互作独立平面运动的图形,在每一瞬时必存在一速度相同的重合点P12,且该点在两速度瞬心的连线上。
首先可以证明其存在性,平面图形上任意点的速度在该瞬时可以用式(3)表示,此时只要满足
则A1和A2速度大小一定相等,所以速度大小相等的重合点一定存在。
再证明该点一定在两速度瞬心的连线上,可用反证法得到。假设该瞬时速度大小相等的重合点为K,此时则满足O1K/O2K=ω2/ω1。在平面图形1 上,K点的速度大小vK1=ω1·O1K,方向垂直于O1K连线;在平面图形2 上,K点的速度大小vK2=ω2·O2K,方向垂直于O2K连线。在图示点虽然速度大小相等,但由于速度方向不同,所以该点不可能。若要满足速度大小和方向均相同,则此重合点只能在O1O2的连线上,记为P12,该点的位置满足O1P12/O2P12=ω2/ω1。
按照点的复合运动分析方法,动点选择平面图形1 上的P12点,动系选择平面图形2,该瞬时绝对运动为以O1点为圆心、O1P12为半径的瞬时圆周运动;牵连运动为绕O2点的瞬时定轴转动。此时绝对速度和牵连速度的大小和方向都相同,由速度合成定理可知vr=0 ,即该动点的相对速度为零。再进一步分析可知,若ω1和ω2的方向相反,则特殊动点P12在两速度瞬心连线之间,反之则在两速度瞬心的延长线上。
2 特殊动点位置的确定
通过直接接触而相对运动的刚体,由于特殊动点具备相对速度为零的特性,因此可以通过以下方法来确定其位置。即:当两个刚体通过光滑圆柱铰链连接时,特殊动点就在铰接点处(图5(a));两刚体处于纯滚动状态时,特殊动点在接触点处(图5(b));两刚体处于滚动兼滑动时,特殊动点在过接触点的公法线上(图5(c))。对于其他情况,可以利用特殊动点在两平面图形速度瞬心(特殊情况为定轴点)连线上这一特性来确定。

图5 特殊动点位置的确定
特殊动点位置确定后,便可以通过点的合成运动分析方法,求解给定刚体的运动学量。
3 实例分析
下面通过相切型实例,利用找特殊动点方法,求解点的复合运动。
3.1 实例一
理论力学授课中经常用图6(a)所示的偏心轮机构(偏心轮为圆形,半径为R,以匀角速度绕定轴D转动)来说明相切型问题“一点两系”的选择,由于此问题没有持续接触点,无论是选择推杆2 还是偏心轮3 上的瞬时接触点为动点,相对运动轨迹都相当复杂,需要借助计算机模拟或者解析求解。为了使得研究问题简单,需要利用推杆BC到偏心轮圆心O距离保持不变的特性,选择偏心轮圆心O为动点,推杆为动系。此时绝对运动为绕D点的圆周运动,牵连运动为竖直方向的直线平移,相对运动为图中红色线所示的直线运动,速度矢量图如图6(a)所示,利用点的速度合成定理
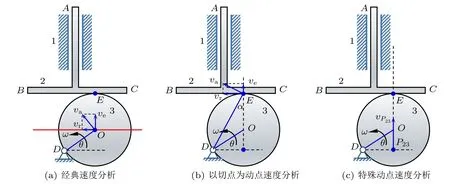
图6 相切型问题速度分析
图6(b)选择偏心轮3 上与BC相切点为动点,推杆2 为动系,相对速度方向为相切点的公切线上,速度矢量图如图6(b)所示。根据速度合成定理
图6(c)给出用本文方法求解过程,根据理论力学中速度瞬心的确定方法可知,D点为偏心轮3 的速度恒为零的点。推杆2 和偏心轮3 是直接接触,它们之间的运动为滚动兼滑动,因此可知该特殊动点在过接触点E的公法线上,过定轴D点作该公法线的垂线可确定唯一交点,此即特殊动点P23。选择偏心轮3 上P23为动点,推杆为动系,由速度合成定理可知
得到的结果与用经典分析方法一致。
从上述3 种速度分析方法可知,经典解法需要利用切点到轮心距离不变的特性,对问题的要求较高;以一刚体上的切点为动点的方法可以求解,此时需要绘制绝对速度、相对速度和牵连速度的矢量图,并严格按照速度合成定理进行分析;本文中的特殊动点方法只要找到该动点后,利用绝对速度与牵连速度相等的特性可以直接求出,求解过程简单且直观。
3.2 实例二
图7 所示为一般平底直动从动件凸轮机构(凸轮为非圆形),已知凸轮的角速度恒为ω,求该瞬时推杆的速度。
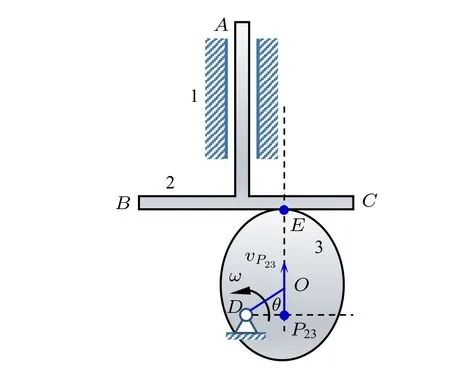
图7 直动从动件凸轮机构速度分析
该问题用理论力学中经典分析方法无法得出,因为无论是选择推杆2 还是凸轮3 上的瞬时接触点为动点,相对运动轨迹都很难得到,这样相对速度的大小和方向都是未知量。但利用本文中的分析方法很容易得到。选择推杆2 为动系,找凸轮3 上的特殊动点,在该点上相对速度为零。寻找特殊动点的方法可以参考3.1 节,得到该特殊动点的位置为P23,如图7 所示。最终推杆的速度大小为
方向如图中所示。
3.3 实例三
图8 所示为摆动从动件凸轮机构(凸轮为非圆形),已知凸轮的角速度恒为ω3,求该瞬时摆杆的角速度ω2。

图8 摆动从动件凸轮机构速度分析
该问题同样因为凸轮不是特定的几何形状,采用经典点的复合运动分析方法无法得到结果。但可以将其转化为寻找特殊动点问题。摆杆2 与凸轮3 是滚动兼滑动,该特殊动点一定在过接触点C的公法线上,此外该特殊动点还需要在AB的连线上,这两条线交点可以唯一确定该特殊动点P23,如图8 所示。摆杆的角速度为
最终求得摆杆的角速度ω2=ω3·AP23/BP23,方向如图所示。
4 结论
本文针对理论力学中任意形状相切型利用经典“一点两系”方法难以确定相对运动轨迹的难题,提出通过寻找特殊动点的方法,很好解决了任意形状相切型点的速度合成分析求解。即通过“该瞬时绝对速度与牵连速度相等”的特性可以对该平面机构进行瞬时速度分析,并给出3 个应用实例。
该方法相比于传统方法,求解过程更加清晰且直观,无需绘制速度矢量图,对只需进行速度分析的少学时工程力学教学有一定的参考价值。主要难点为如何寻找特殊动点位置。特殊动点的位置一定在两平面图形速度瞬心(特殊情况为定轴点)的连线上,也在相切点公法线上;当两个相切刚体中一个刚体作直线平移,另一个刚体作定轴转动时,这个特殊动点为定轴点作公法线的垂线,与公法线的交点。这一分析方法也为机械专业后续机械原理课程的学习打下基础,改善不同科目间知识割裂或者跳跃性较大的现状,让学生更加注重课程知识体系的内在联系,注重知识的互通。
在理论力学日常的教学中一般是先讲授点的合成运动,然后再讲授刚体的平面运动,本方法交叉应用了点的合成运动及刚体平面运动中的速度瞬心法,对提高学生对整体知识的把握有益,在教学过程中取得了良好的效果。