爆炸载荷下顺层台阶边坡渐进破坏规律数值分析1)

姚作强 * 冯 春 ** 刘天苹

*(北京市工程咨询有限公司，北京 100124)

†(中国科学院力学研究所流固耦合系统力学重点实验室，北京 100190)

**(中国科学院大学工程科学学院，北京 100049)

台阶爆破在露天矿开采，水电边坡、公路（铁路）沿线边坡开挖等方面广泛应用。在台阶爆破过程中，爆破产生的应力波将对后方的高陡边坡产生影响。近距离或大当量爆破过程中，在应力波反复作用下，边坡内部的薄弱结构面将逐渐出现失稳贯通，最终可能导致边坡出现整体性滑动。因此，台阶边坡的爆破稳定性问题一直受到工程界及学术界的持续关注[1-7]。

数值模拟因其能揭示爆破作用下边坡内部应力波的传播规律及宏观裂缝的渐进扩展规律，因此被广泛应用于边坡爆破稳定性的分析中。占绍祥等[8]和张卉等[9]重点分析了爆破开挖过程中Hoek–Brown 扰动系数与边坡稳定性的对应关系，并指出采用扰动系数渐进弱化的方式，可较好反映爆破损伤对边坡稳定的影响。王建国等[10]利用FLAC3D 软件，通过施加实测地震波的方式，探讨了布沼坝露天煤层西帮边坡的动态规律。周后友等[11]借助ANSYS 分析了别矿露天边坡在静力和动力下的稳定性，给出了该边坡在爆破载荷下的安全振速和临界振速。吴燕开等[12]采用ABAQUS分析了爆炸载荷下岩石的振动效应，给出了岩质高边坡在动力作用下的位移演化规律及振动规律。马冲等[13]借助FLAC3D 探讨了爆破载荷对边坡振速规律的影响，并建立了爆破振速安全阈值。

目前，边坡爆破稳定性的常用数值模拟方法包括有限元法、离散元法和有限差分法等。有限单元法通过在表征元上引入宏观动力学本构，实现了爆炸载荷下边坡弹塑性变形过程的精确模拟，但却无法准确刻画边坡内部结构面的渐进失稳过程及边坡整体失稳后的运动成灾过程。离散元方法适用于模拟真实颗粒体系的碰撞运动过程，但在模拟连续介质弹塑性变形方面精度较差。连续–非连续单元方法(continuum–discontinuum element method，CDEM)[14-20]通过将连续介质数值模拟方法（如有限元法）及非连续介质数值模拟方法（如离散元法）进行有机结合，实现了地质体弹性、塑性、损伤、断裂、破碎、运动、碰撞、堆积的全过程模拟。

总体而言，目前边坡爆破稳定性的数值分析大都基于场地实测获得的加速度（速度）时程曲线展开，没有实现炸药起爆、应力波传播、边坡振动破坏的全过程耦合。事实上，由于受场地条件及地层特性的影响，地表测得的振动时程曲线与通过岩体内部传递至坡体的应力波并不完全等价，因此上述将爆破过程与边坡失稳过程割裂开来的分析方法，无法准确反映爆破对边坡的损伤破坏作用。此外，目前的数值模拟大都以连续介质方法（如有限元法、有限差分法）为主，无法准确刻画爆炸载荷下结构面岩体的渐进破裂过程及失稳后的运动成灾过程。因此，本文将以CDEM的数值计算代码为基础，通过引入考虑应变率效应的岩体及结构面动力损伤破裂力学模型及爆生气体的膨胀模型，编制C++ 数值计算代码，直接模拟三维情况下爆破对顺层岩质边坡的影响，并重点探讨爆破参数及结构面参数对边坡稳定性的影响规律。

1 计算方法及本构模型

1.1 CDEM 计算方法

CDEM 是一种以广义拉格朗日方程为基本框架的显式动力学数值方法。该方法将基于连续与非连续介质的两类数值方法进行深度融合，在能量层面实现了有限元法、离散元法及无网格法的统一，可模拟地质体及人工材料在静、动力载荷下的弹性、塑性、损伤及破裂过程，以及破碎后散体的运动、碰撞、流动及堆积过程。CDEM 中每个单元均具有独立的节点及独立的面，相邻两个单元依靠粘接界面进行连接；利用单元表征材料宏观连续介质特性，利用粘接界面表征材料的断裂滑移等非连续介质特性（图1）。

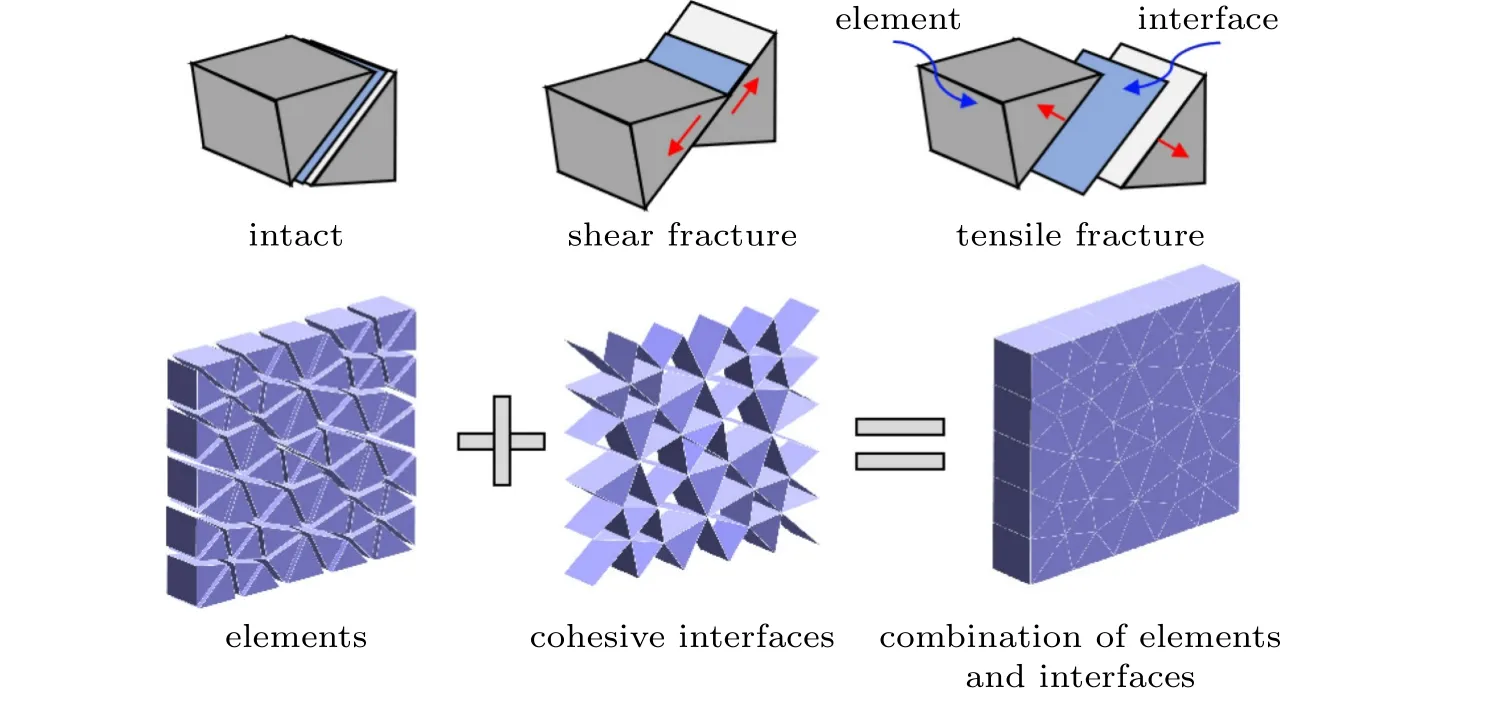
图1 CDEM 中的断裂描述Fig.1 Description of fracture in CDEM

CDEM 采用增量显式迭代法进行动力问题的求解，主要迭代过程包括节点合力的求解及节点运动过程的求解两个方面。

节点合力计算公式为

式中，F为节点合力，FE为节点外力，Fe为有限元单元变形贡献的节点力，Fc为界面接触在节点上贡献的接触力，Fr为瑞利阻尼在节点上贡献的节点阻尼力，Fl为节点局部阻尼力。

节点运动计算公式为

式中，a为节点加速度，v为节点速度， ∆u为节点位移增量，u为节点位移，m为节点质量，∆t为计算时步。

基于式（1）及式（2）的交替计算即为显式求解过程。

1.2 边坡岩体本构模型

为了精确描述爆炸载荷下岩体的动力学行为及渐进破坏过程，本文提出了考虑应变率效应及损伤破裂效应的单元–界面双重本构，采用考虑动力增强效应的Mohr–Coulomb 应变软化模型对边坡的实体单元进行描述，采用考虑应变率效应的断裂能本构对岩体结构面进行描述。

（1）实体单元本构[21]

首先判断当前应力状态是否已经达到或超过Mohr–Coulomb 准则及最大拉应力准则，为

式中，fs为Mohr–Coulomb 屈服函数；ft为最大拉应力屈服函数；h为Mohr–Coulomb 屈服函数与最大拉应力屈服函数的角平分线（用于判定失效模式）；σ1和σ3为最小主应力及最大主应力；σt(t)，c(t)，ϕ为当前步抗拉强度、黏聚力及内摩擦角；αp，σp，Nϕ为常数；η 及ξ 分别为拉伸应变率增强因子及剪切应变率增强因子。

η 及ξ 可表述为

式中，θ˙ 及γ˙ 为体应变率及等效剪应变率，e1及e2为单元应变率效应指数，本文取e1=e2=1/3。˙

θ及 ˙γ可表述为

式（3）中，如果fs≥0 且h≤0，单元发生剪切塑性变形；如果ft≥0 且h>0，则发生拉伸塑性变形。

单元发生塑性变形后，采用式（6）对黏聚力及抗拉强度进行折减，为

式中，Δt为计算步长，σt0和c0为抗拉强度及黏聚力的初始值，εp和εlim为当前时刻拉伸塑性应变及拉伸断裂应变，γp和γlim为当前时刻剪切塑性应变及剪切断裂应变，c(t+Δt)和σt(t+Δt)为下一时刻的黏聚力及抗拉强度。

本文采用非关联流动法则对实体单元的塑性流动行为进行描述，故需在流动法则中引入剪胀角Ψ。

（2）界面本构

边坡岩体中结构面的密度、产状（倾向、倾角）及力学参数等均会对边坡的爆破稳定性产生重要影响，在数值模拟时需要重点考虑。其中，岩体结构面的密度、产状等几何参数，在建立边坡模型及划分网格时直接进行考虑；对于力学参数，则需要通过结构面力学本构进行体现。

本文采用考虑应变率效应的断裂能本构，对岩体结构面及岩块虚拟界面在爆炸载荷下的损伤破裂行为进行精确描述。

首先计算法向试探接触力，进行拉伸破坏判定，并对法向接触力及抗拉强度进行修正，为

式中，Fn(t1)为下一时步法向接触力；Ac为虚拟界面接触面积；σt0，σt(t0)及σt(t1)为虚拟界面上抗拉强度的初始值、当前值及下一时刻的值；Δun为虚拟界面上法向相对位移的当前值，Gft为虚拟界面拉伸断裂能（单位：Pa⋅m）。

接着进行切向试探接触力的计算，剪切破坏的判定，并对切向接触力及黏聚力进行修正，为

式中，Fs(t1)为下一时步切向接触力；ϕ为界面上的内摩擦角；c0，c(t0)及c(t1)为界面上黏聚力的初始值、当前值及下一时刻的值；Δus为界面上切向相对位移的当前值；Gfs为界面的剪切断裂能（单位：Pa⋅m）。

当考虑应变率的影响时，初始黏聚力及初始抗拉强度与应变率之间有如下函数关系

式中，γ˙ 及ε˙ 为界面上的剪切应变率及拉伸应变率，e1及e2为界面应变率效应指数，本文取e1=e2=1/3。

1.3 爆生气体膨胀模型及与围岩的耦合

本文假定爆轰过程瞬间完成，并借助朗道–斯坦纽科维奇方程（γ 率方程）对爆生气体的膨胀过程进行刻画，该方程可表述为

式中，取γ 为3，γ1为4/3，P0和P分别表示初始时刻、当前时刻的爆生气体压力，V0和V分别表示初始时刻、当前时刻的爆生气体体积。Pk和Vk分别为爆生气体的临界压力及临界体积，Pk的表达式为

式中，Qw为炸药爆热（J/kg），ρw为炸药密度（kg/m3）。

P0的表达式为

式中，D为爆轰速度（m/s）。

爆生气体与围岩的耦合采用接触耦合方式实现，通过法向耦合弹簧，将爆生气体产生的压力渐进地传递给围岩；围岩单元间的法向弹簧及切向弹簧在爆炸压力的作用下，出现拉伸变形及剪切变形，进而出现拉伸断裂及剪切断裂。爆生气体与围岩的耦合示意图如图2 所示。

图2 爆生气体单元与岩石单元的耦合Fig.2 Coupling between blasting gas elements and rock elements

爆生气体与围岩的接触力计算公式可表示为

式中，Fc为法向接触力，Kn为接触刚度，Δun为法向接触位移（拉为正，压为负）。

由于本文重点关注爆炸应力波对周边顺层边坡渐进破坏规律的影响，故本节提出的爆生气体与围岩的耦合模型仅考虑了爆生气体对围岩岩壁的冲击作用（爆炸应力波产生的主要来源），但未考虑爆生气体楔入岩体裂缝的过程。

1.4 力学模型的数值化嵌入

采用C++ 语言，将上述边坡岩体本构模型及爆生气体膨胀模型代码化，嵌入至CDEM 的主体程序中。其中，岩体本构模型将拆分成单元本构及接触面本构，分别从CDEM 程序中的单元本构类及接触面本构类进行派生；同样，爆生气体膨胀模型也将从单元本构类中进行派生，爆生气体与围岩之间的接触模型则从接触面本构类中进行派生。

力学模型数值化嵌入CDEM 主程序后，将依附于主程序求解框架进行动态求解，单步求解流程如图3 所示。图中红色虚线框部分为本文主要涉及的力学模型及求解流程。

图3 单步求解流程Fig.3 Solution flow in each time step

2 计算方法及力学模型的案例验证

对文献[22]中的爆破漏斗实验进行数值模拟。该文中的爆破对象为人工材料，由水泥、石膏、河砂、碎石组成，质量分数为1.00∶0.45∶3.82∶3.82。将该人工材料倒入高强度PVC 模具中，在自然条件下28 d 后制成直径57 cm，高度50 cm的圆柱体试件。在模型中部放入4.5 g TNT 炸药，埋深17 cm。具体的试验步骤、方法及试验材料介绍详见文献[22]，此处不再赘述。

为了模拟爆破漏斗试验，建立了相同尺寸的圆柱体模型（图4），并用162 744 个四面体单元进行离散。在模型的底部施加全约束边界条件，在模型的侧面施加法向约束条件，模型的顶部为自由面。

图4 爆破漏斗数值模型Fig.4 Numerical model of blasting crater

人工材料数值模型由单元及虚拟界面组成，单元采用线弹性本构进行描述，虚拟界面采用断裂能本构进行描述。TNT 炸药采用朗道爆生气体膨胀模型进行描述，炸药参数取值主要来自文献[22]，其中炸药密度为1400 kg/m3，爆速为4700 m/s，爆热为3.0 MJ/kg。炸药及人工材料间采用法向接触弹簧进行耦合。人工材料的参数如表1 所示，材料参数主要根据文献[22]中的材料配合比及文献[23-24]中关于材料配合比与材料参数的关系综合确定。

表1 人工材料计算参数Table 1 Computation parameters of artificial material

起爆后，材料的渐进破坏过程及破碎块体的运动过程如图5 所示。由图可以看出，起爆后0.5 ms 时顶面出现了若干径向裂缝；起爆后3 ms时顶面中部开始隆起；6 ms 后顶部岩体出现大量破裂，内部碎片向外喷出；20 ms 后爆坑已经基本形成。

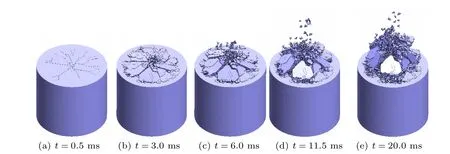
图5 人工材料的渐进破坏过程及碎块运动过程Fig.5 Progressive failure and fragments movement process of artificial material

数值模拟和物理实验的爆坑对比如图6 所示。从图中可以看出，数值模拟得到的爆坑形态、直径与物理实验得到的爆坑形状及直径基本相同，验证了CDEM 模拟岩土爆破问题的准确性和合理性。

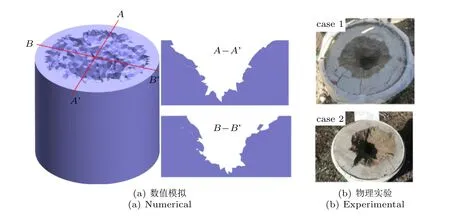
图6 数值模拟与物理实验的爆坑形态对比Fig.6 Comparison of craters between numerical simulation and physical experiment

模型顶部中点的位移时程曲线如图7 所示，其中实验部分的位移–时间曲线由高速摄影拍摄的视频解析所得。由图可得，数值计算获得的顶部位移随时间的变化曲线与现场实验的结果基本一致，平均误差在15%左右，满足工程精度要求。

图7 模型顶部中点位移时程曲线的对比Fig.7 Comparison of displacement of middle point on the top side

需要说明的是，文献[22]中的实验对象为人工均质材料，并没有设置结构面。本文对该模型实验进行模拟对比，主要是为了验证本文提出的岩体损伤破裂模型及爆生气体–固体耦合算法的正确性。从图6 和图7 的对比分析可以看出，本文提出的力学模型及耦合方法用于模拟爆破载荷下岩体的动力学行为是适宜的，计算精度可以保证。

3 爆破开采对顺层边坡稳定性的影响

3.1 计算模型及参数

以鞍千矿业哑巴岭矿区的台阶边坡爆破稳定性分析为例。矿区内出露的地层主要为前震旦纪鞍山群及辽河群变质岩系。岩层主要包括赤铁矿、片岩、灰岩、千枚岩等，地层走向140°，倾向为SW，倾角小于50°。矿区内岩体受结构面切割，形成多处顺层台阶边坡。

概化后的台阶边坡计算模型及炮孔位置如图8 所示。边坡的台阶高度12 m，台阶坡面角65°，平台宽度2.6 m，边坡帮坡角55°；炮孔直径25 cm，孔深15 m，填塞7 m，炮孔到坡脚的距离为6 m。该图中，编号1，2，3，4，5 表示5 种不同倾角的结构面，结构面倾角分别为10°，20°，30°，40°及50°。

图8 结构面边坡数值模型Fig.8 Numerical model of jointed slope

炮孔内炸药为现场混装的乳化炸药，采用爆生气体膨胀模型进行描述，爆生气体与围岩的耦合采用接触耦合方式进行模拟。乳化炸药的密度为1150 kg/m3，爆速为4250 m/s，爆热为3.4 MJ/kg。

计算过程中，为了消除爆炸应力波在人工截断边界处的虚假发射现象，本文在模型的底部及四周引入了黏性边界。

台阶边坡的力学参数来自文献[14]，具体如表2 所示。

表2 铁矿边坡实体单元计算参数Table 2 Computation parameters of solid elements of iron ore slope

顺层结构面的结构面角度为50°，黏聚力为0.1 MPa，抗拉强度为0.1 MPa，内摩擦角为30°，拉伸断裂能为10.0 Pa⋅m，剪切断裂能为50.0 Pa⋅m。

采用单因素法，分别探讨不同爆破距离、不同顺层面倾角及不同顺层面强度下，爆破对后方台阶边坡稳定性的影响。讨论某一变量的影响时，其他参数取上述基础参数。

对于结构面倾角及爆破距离，将在建立边坡几何模型时直接考虑。其中，结构面建模时，以结构面位置及倾角为界，将边坡切割为不同的体；炮孔建模时，根据设定距离建立圆柱形炮孔，并与边坡模型进行求交操作。对于顺层面强度，则在数值计算中通过考虑应变率效应的结构面断裂能本构进行体现。

3.2 爆破距离的影响

研究爆破距离对贯穿性结构面边坡的影响规律，共探讨6 种爆破距离的影响。结构面角度为50°，爆破距离分别为3 m，6 m，9 m，12 m，15 m 和18 m。典型爆破距离下结构面边坡的水平方向位移云图如图9 所示（图中黑线表示破裂面）。由图可得，随着爆破距离的增加，结构面贯穿程度逐渐减小，但变化并不明显。

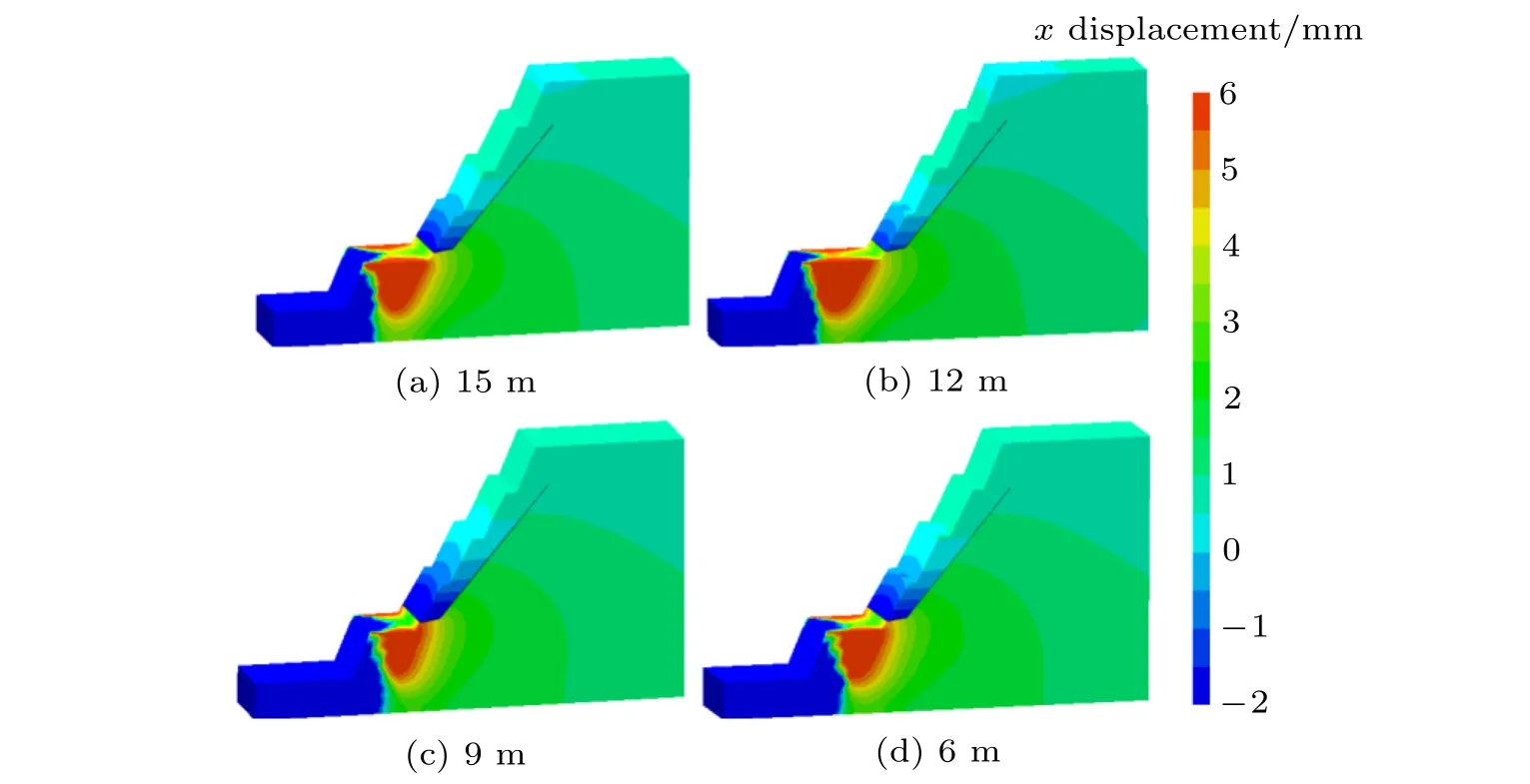
图9 不同爆破距离下结构面边坡水平方向位移云图Fig.9 Horizontal displacement contour of jointed slope under different blasting distances

结构面的破裂面积随爆破距离的变化曲线如图10 所示。从曲线可看出，当爆破距离从3 m增大至18 m，结构面的破裂面积从1060 m2减小至820 m2，减小比例23%。

3.3 结构面角度的影响

共探讨5 种结构面贯穿角度的工况，分别命名为工况1～5（如图8 所示），工况1～5 对应的贯穿结构面角度分别为10°，20°，30°，40°及50°。

数值计算结果表明，当炮孔距离坡脚为6 m时，爆破载荷对工况1～4 的结构面边坡无影响，爆破完成后边坡仍处于稳定状态，结构面也并未出现破坏。但该爆破距离下的爆破载荷对工况5的结构面边坡（结构面角度为50°）影响较大，导致该边坡的结构面出现了整体破坏，并最终造成边坡失稳。爆破作用下结构面的破坏模式主要为拉–剪复合型破坏，当结构面完全破坏后，上覆岩体将沿着结构面发生整体滑动，如图11(a)所示（图中蓝色表示未破坏，黄色表示拉伸破坏，红色表示剪切破坏）。从位移云图（图11(b)）可以看出，结构面两侧的位移出现了不连续，表明边坡已沿着结构面发生了整体滑移，边坡处于失稳状态。

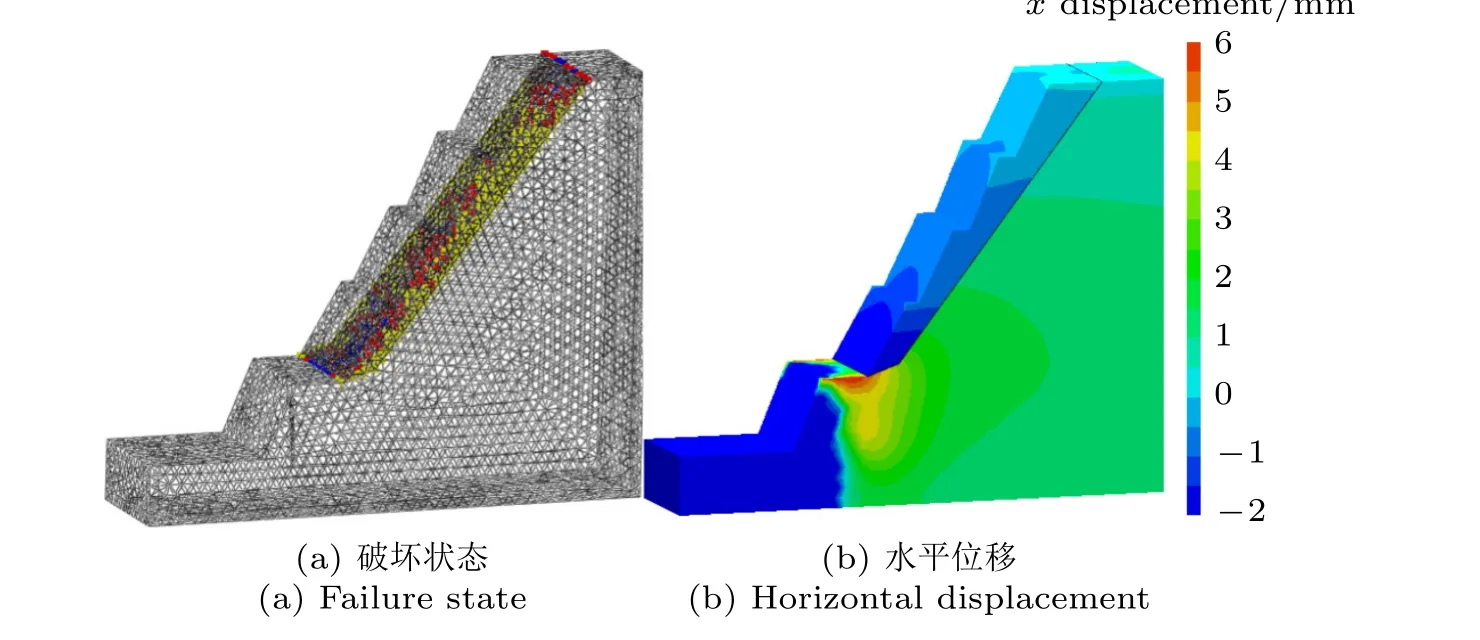
图11 结构面角度50°时的破坏状态Fig.11 Failure state of structural surface with the dip angle 50 degree

3.4 结构面强度的影响

取炮孔到坡脚的距离为15 m，结构面角度为50°，研究结构面强度对边坡稳定性的影响。文中采用Mohr–Coulomb 准则描述结构面的压剪破坏，主要涉及的强度参数包括黏聚力及内摩擦角；采用最大拉应力准则描述结构面的拉伸破坏，主要涉及的强度参数为抗拉强度。本节共选取6 组结构面强度进行探讨，每组强度参数中的内摩擦角保持一致，为30°，且每组中结构面的黏聚力和抗拉强度取相同值（即c=σt，以下统称为结构面强度）。所选取的结构面强度值分别为0.2 MPa，0.6 MPa，1.0 MPa，1.4 MPa，1.8 MPa 和2.2 MPa。

结构面强度为0.2 MPa，0.6 MPa，1.0 MPa和1.4 MPa 时的边坡水平方向位移云图如图12所示。从图中可以看出，结构面强度对结构面破坏程度的影响较大，随着结构面强度的增加，结构面贯穿程度逐渐减小。

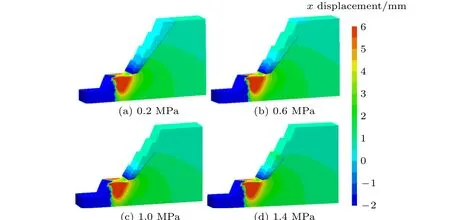
图12 不同结构面强度下结构面边坡水平方向位移云图Fig.12 Horizontal displacement contour of jointed slope under different structural surface strength

结构面破裂面积随结构面强度的变化曲线如图13 所示。从曲线可看出，结构面破裂面积随着结构面强度的增大而逐渐减小；当结构面强度从0.2 MPa 增大至1.4 MPa，破裂面积从1156 m2减小至337 m2，减小了71%。

图13 爆破载荷下结构面破裂面积随结构面强度的变化曲线Fig.13 Relationship between fracture area and strength of structural surface under blasting load

3.5 讨论

炮孔内炸药起爆后，爆炸能量一部分用于台阶自由面附近的岩体破碎，另一部分则向远处传播。当爆炸应力波沿着台阶逐渐向后方传递，并进一步传递至台阶上方边坡时，若边坡内存在软弱结构面，在直达剪切波及坡面反射拉伸波的双重作用下，或将导致结构面出现拉剪复合型破坏，并进一步诱发顺层边坡出现整体性失稳滑动。

文章借助CDEM 方法，利用单元表征岩体的变形特性，利用单元间的界面表征结构面的断裂滑移效应，详细探讨了爆破距离、结构面产状及结构面强度等因素对顺层边坡结构面破坏程度的影响。根据前述计算分析可以看出，由于坡脚处的动应力最大，且坡脚处所受的切向应力最大，因此顺层结构面的破裂失稳首先出现在坡脚附近。一旦坡脚处出现破裂，结构面上的整体平衡被打破，裂缝将在动力作用下进一步向坡体中上部的结构面发展。随着到坡脚距离的增大，动应力峰值逐渐减小，对结构面的扰动也逐渐减小，一旦扰动应力幅值小于结构面上未破裂区域的强度，弱面的破裂失稳过程随即停止。若减小炮孔到边坡坡脚的距离，或提升单孔装药量，即使爆炸应力波将随着边坡高程的增加逐渐减少，但仍然有足够的能力诱使顺层结构面出现整体破裂，届时顺层滑体将会沿着软弱结构面整体下滑，出现顺层滑坡灾害。爆破载荷下顺层边坡的失稳机理示意图如图14 所示。

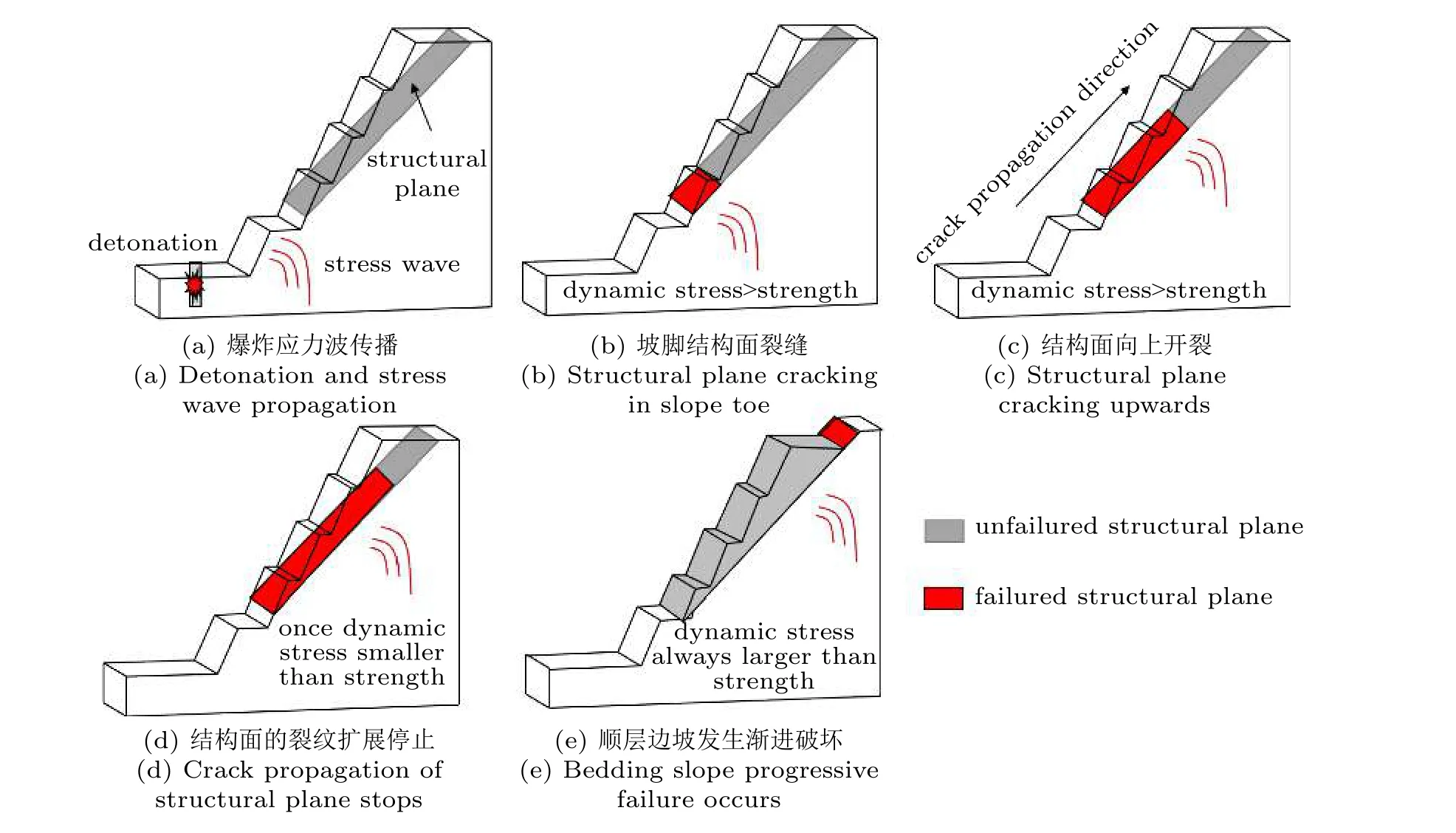
图14 爆破载荷下顺层边坡的失稳机理Fig.14 Failure mechanism of bedding rock slope under blasting load

4 结论

本文以CDEM 为基础，通过引入考虑应变率效应及应变软化效应的摩尔–库伦单元本构模型、考虑应变率效应的界面断裂能模型、以及爆生气体绝热膨胀及与围岩的耦合模型，实现了炸药起爆—爆炸应力波传播—边坡渐进破裂的全过程模拟。通过爆破漏斗的数值试验，证明了本文所提出的力学模型及所编制的计算程序在刻画爆炸载荷下岩体损伤破裂过程方面的优势。

借助本文提出的力学模型，开展了爆破作用下顺层台阶边坡渐进破坏规律的研究，揭示了爆破载荷下顺层边坡的失稳破坏机理，探讨了炮孔到边坡的距离、结构面产状、结构面强度等因素对顺层边坡稳定性的影响规律，所得结论如下。

（1）在爆炸应力波的直接压剪作用及坡面反射波的拉伸作用下，顺层结构面易发生拉剪复合型破坏；一旦结构面整体破坏，上覆顺层滑体将沿着结构面出现整体性滑动。

（2）结构面倾角越大、结构面强度越低、炮孔到边坡的距离越小，顺层边坡越容易在爆炸载荷下出现动力失稳；在文章计算参数范围内，相较于炮孔到边坡的距离，结构面强度对边坡爆破稳定性的影响更为显著。

本文揭示的顺层台阶边坡爆破失稳机理，给出的爆破距离、结构面产状、结构面强度等参数对顺层边坡爆破稳定性的影响规律，将有助于工程设计人员及现场工作人员确定合理的台阶边坡参数及爆破安全距离，并将对边坡爆破稳定性的预警分析起到一定的指导作用。

后续将重点开展反倾边坡、块状岩体边坡等岩质边坡在爆炸载荷下的渐进破坏规律分析，通过调整边坡结构面参数、炸药参数及孔网参数等，开展大量的仿真分析，形成爆破载荷下边坡稳定性及变形破坏特征的仿真数据库，借助机器学习算法构建边坡爆破分析降阶模型，以期为边坡爆破稳定性的设计评估提供快速分析的工具。