卧式螺旋卸料沉降离心机螺旋空心轴内表面磨损的研究

袁惠新，王伟鹏，付双成，戴如昊，周发戚

（常州大学 机械与轨道交通学院 江苏省绿色过程装备重点实验室，江苏常州 213164）

0 引言

卧式螺旋卸料沉降离心机（亦称卧螺离心机或简称卧螺）是一种固-液两相或固-液-液三相分离设备，能够连续自动排渣，相比于过滤机等具有单机处理能力大、操作方便、连续操作、占地面积少以及维护费用低等优点［1-2］。这使得卧螺离心机成为工业应用中物料的脱水、澄清、轻固相分离中优先考虑的设备［3-5］。如图1所示，物料从进料管进入螺旋空心轴，再从螺旋空心轴的出料口进入离心机转鼓内进行离心沉降分离［6］。螺旋空心轴内腔起到对进料的加速作用，外壁的螺旋起到输渣的作用，是卧螺离心机的一个关键部件，但工程实践中常常发现内壁被冲刷，甚至被切割出沟槽（如图2所示），使得螺旋空心轴产生局部磨损，严重可致使空心轴磨穿漏料，甚至导致质心偏移，引起设备的强烈振动，酿成事故。

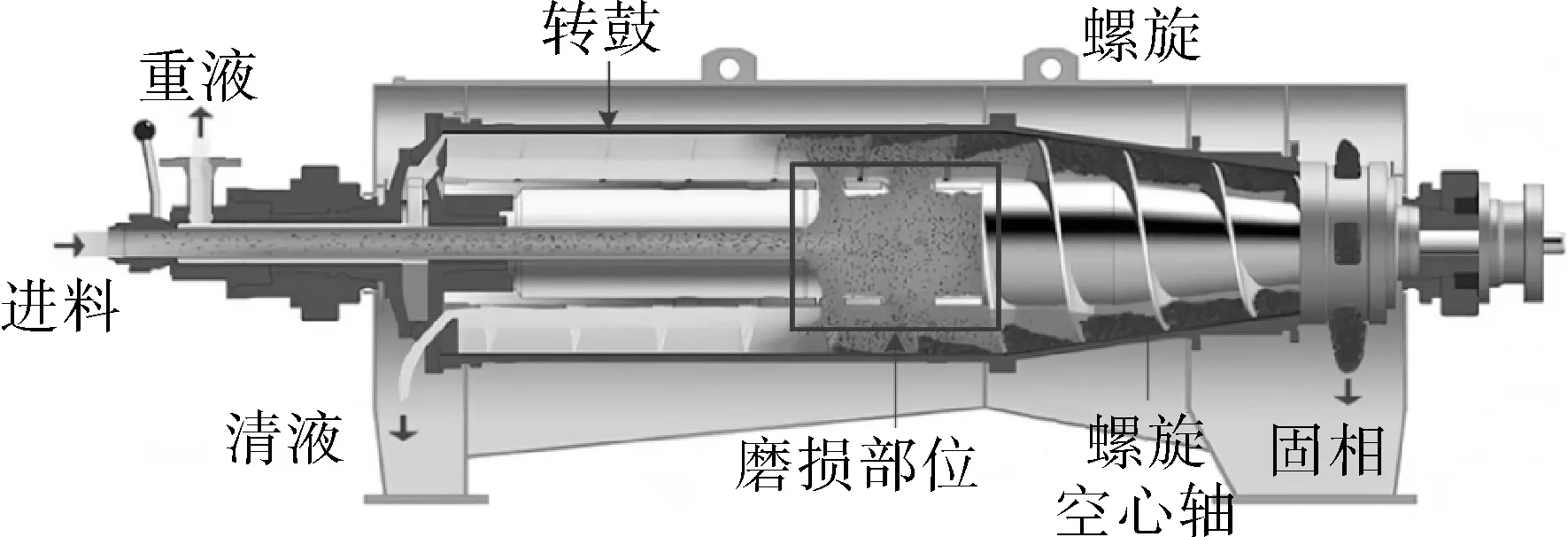
图1 卧螺离心机结构示意Fig.1 Schematic diagram of the decanter centrifuge structure

图2 螺旋空心轴内的磨损情况Fig.2 Erosion inside the spiral hollow shaft

流体力学（CFD）方法被广泛应用于流体机械的磨损分析及结构优化计算中，为流体机械在应用中的减磨防磨提供了计算方法。刘丽艳等［7］基于Euler-Euler多相流模型在多重参考系坐标下，通过剪切力间接表征了进料加速器内壁面的磨损情况；谭蔚等［8］利用Tabakoff模型分析了进料流量和转速对卧螺离心机进料分布器的磨损影响，证明了磨损模型在旋转机械研究中的可行性，并通过搭建PIV可视化试验台对其内部流场进行验证。CHEN等［9］通过简化仿真模拟和试验的方法进行了圆盘上V形、U形和环形槽的主要形状、尺寸对磨损的影响。刘栋等［10］通过数值模拟方法，计算了离心泵叶轮的磨损，并发现叶片出口安放角、进口安放角和包角显著影响了离心泵叶轮的磨损特性。HAN等［11-12］研究了低碳钢表面上沟槽的结构对抗冲蚀性能的影响，由于流动状态的改变，一部分颗粒改变了原有的冲击角度，致使磨损率发生改变。WANG等［13］基于数值模拟，在预测磨损率时考虑了基于磨损时间的弯管表面的结构演变。国内外对卧螺离心机螺旋空心轴内壁磨损的研究鲜有报道。因此，针对某企业小型卧螺离心机出现的磨损，通过试验和CFD模拟，研究主要操作参数和结构参数对螺旋空心轴内圆柱壁面磨损的影响规律。但限于篇幅，离心机的转速、沙粒大小等影响不在本文中介绍。

1 研究方法

1.1 试验方法

水中的砂子会在空心轴旋转的过程中与壁面撞击并导致壁面出现质量损失。本试验使用中位粒径为80 μm的石英砂配置体积浓度为1%的水沙悬浮液作为试验物料，在空心轴内壁设置磨损试件进行磨损试验，磨损试件由铝制成，且长和宽均为30 mm，厚度为1.8 mm，表面用砂纸抛光，并用1 mg电子天平对磨损试件进行试验前后称重来反映空心轴壁面磨损程度。

试验流程如图3所示，试验装置主要由料桶、搅拌桨、离心泵、转子流量计和磨损试验装置组成，通过离心泵将物料以一定的初速度送入磨损试验装置来达到模拟螺旋空心轴工作的过程。在试验过程中，搅拌桶的物料温度被控制在10 ℃左右，并通过搅拌桨持续搅拌，以免石英砂沉降分层而影响进料的稳定性。流量控制范围在1.37～2.74 m3/h，转速设定为1 200 r/min。由于磨损试验需要的时间周期长，本试验中，物料循环使用，以保证进料条件的稳定性。

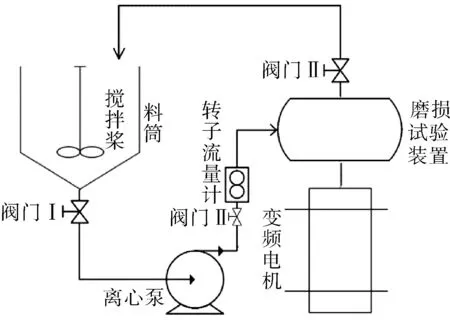
图3 试验流程Fig.3 Experimental flow chart

1.2 模拟方法

1.2.1 物理模型建立

图4示出小规格螺旋空心轴的内壁面简图，计算域共分为射流域和旋转域2个部分。为了更好地研究磨损并节省计算资源，将螺旋空心轴受螺旋影响而分布不均匀的出口在周向均匀分布。在内壁面的某一周向位置设置正方形边长为30 mm、厚度为1.8 mm的试件为微凸起，或圆形直径为2 mm、深度为0.5 mm的凹陷。具体参数见表1。

表1 空心轴主要结构参数Tab.1 Main structural parameters of the hollow shaft mm

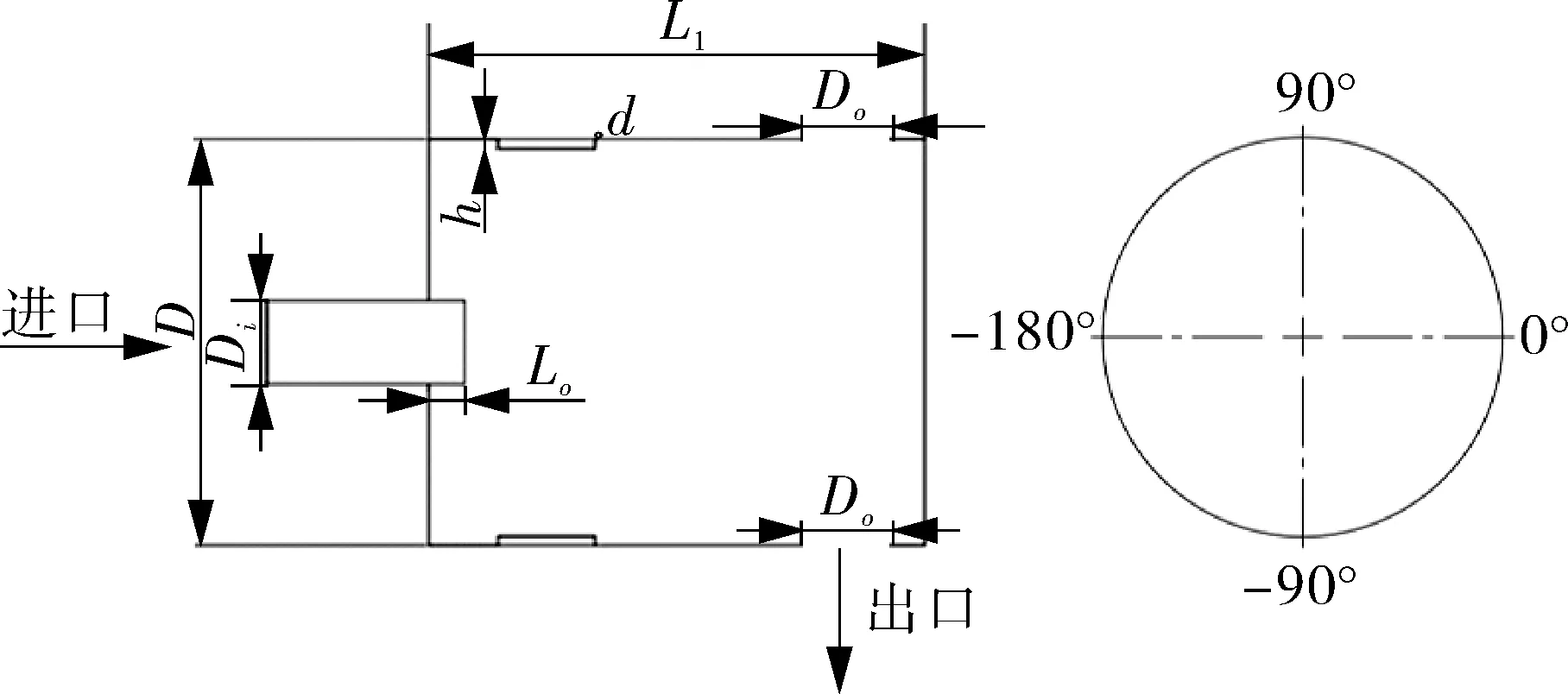
图4 空心轴结构Fig.4 Schematic diagram of hollow shaft structure

1.2.2 液相计算模型

因为卧螺离心机是高速旋转设备，所以本模拟采用RNG湍流模型。RNG湍流模型提高了高速流动模拟的准确性且该模型考虑了涡流对湍流的影响，提高了旋涡流动的精度，可以更好地模拟旋转流动的体系，并采用多重参考系模型（MRF）来模拟螺旋空心轴内的两相流动。由于忽略液相的压缩性和相变，且不考虑温度的影响，所以RNG k-ε模型的运输方程为：

1.2.3 颗粒相计算模型

采用欧拉-拉格朗日方法计算固液两相流动，在拉格朗日坐标下对颗粒的运动方程积分来获取例子轨迹。根据SIAFM［12］的研究表明，当粒子的质量载荷不大于1时，可以忽略粒子间的碰撞，本研究就是这种情况。粒子运动的控制方程可以表示为：

式中，mp为颗粒质量；为颗粒流速；为曳力；为压力梯度力；为虚拟质量力；ρp为颗粒密度；dp为颗粒直径；Cd为曳力系数，对于球形颗粒，取Cd=1；μ1为水的动力黏度；Re为颗粒雷诺数。

湍流的脉动速度对颗粒运动有很大影响，故本文采用颗粒随机轨道模型（Discrete Random Walk Model），来实现湍流与颗粒运动之间的耦合。

1.2.4 磨损计算模型

磨损模型可以监测到泥沙颗粒在壁面的磨损情况。本文选用FLUENT中的Mclaury磨损模型。磨损率与泥沙物质成分、流速、壁面材料、冲击角度和运行情况等因素有关。冲蚀速率的定义为：

式中，Rero为泥沙的冲蚀速率，kg/（m2·s）；˙mp为单位时间颗粒对壁面磨损掉的材料质量；C（dp）为颗粒的径粒函数；α为颗粒对壁面的冲击角；f（α）为冲击角函数；v为颗粒相对于壁面的速度，m/s；b（v）代表颗粒相对速度函数；Aface为颗粒向壁面的投影面积。

在仿真中的磨损试件的磨损量是通过后处理软件求得磨损试件表面的平均磨损率，然后再通过以下公式来进行定义：

式中，Em为磨损试件的磨损量；Eave为磨损试件的表面平均磨损率；S为磨损试件的表面积；T为磨损试验需要的时间。

1.2.5 边界条件设置和计算方法

边界条件设置如下。

入口边界：水流入口边界设置为速度入口，流速大小随着进料流量变化；离散相的流速与水流速度相同。

出口边界：出口边界设置为压力出口。

壁面边界：壁面采用无滑移固体边界，近壁区域的流动使用标准壁面函数来模拟，空心轴转速设置为1 200 r/min。离散相与所有的固体边界的接触方式设置为reflect。

本文计算选用GRANT等［15］提出的弹性碰撞恢复模型，其中en为法向恢复系数，et为切向恢复系数，θ为碰撞角度。

2 结果与讨论

2.1 处理量对微凸起试件磨损的影响

2.1.1 螺旋空心轴内表面有微凸起时的流场及磨损

图5示出螺旋空心轴内表面有微凸起（h=1.8 mm）时的速度云图。由图中可以看出，圆筒内部流体的速度总体上呈中心对称分布，速度的大小随着径向半径的增加逐渐增大。从微凸起处局部流体速度的等值线看出，微凸起处的流体迎流面速度大于其背流面速度，微凸起处形成回流区，微凸起下游回流区的形成过程为：流体在微凸起角点处与固体壁面分离，之后再附于台阶下游壁面，下游壁面上方局部区域内的流体形成回流运动。所以在微凸起的底部位置的磨损率会更高。从图6可知，粒子在离心力和微凸起的作用下，影响了粒子本有的运动轨迹，使得微凸起进料端附近壁面的磨损率会变高，其不同方位角下磨损率的关系如图7所示。微凸起进料侧具有一定的磨损集中现象。

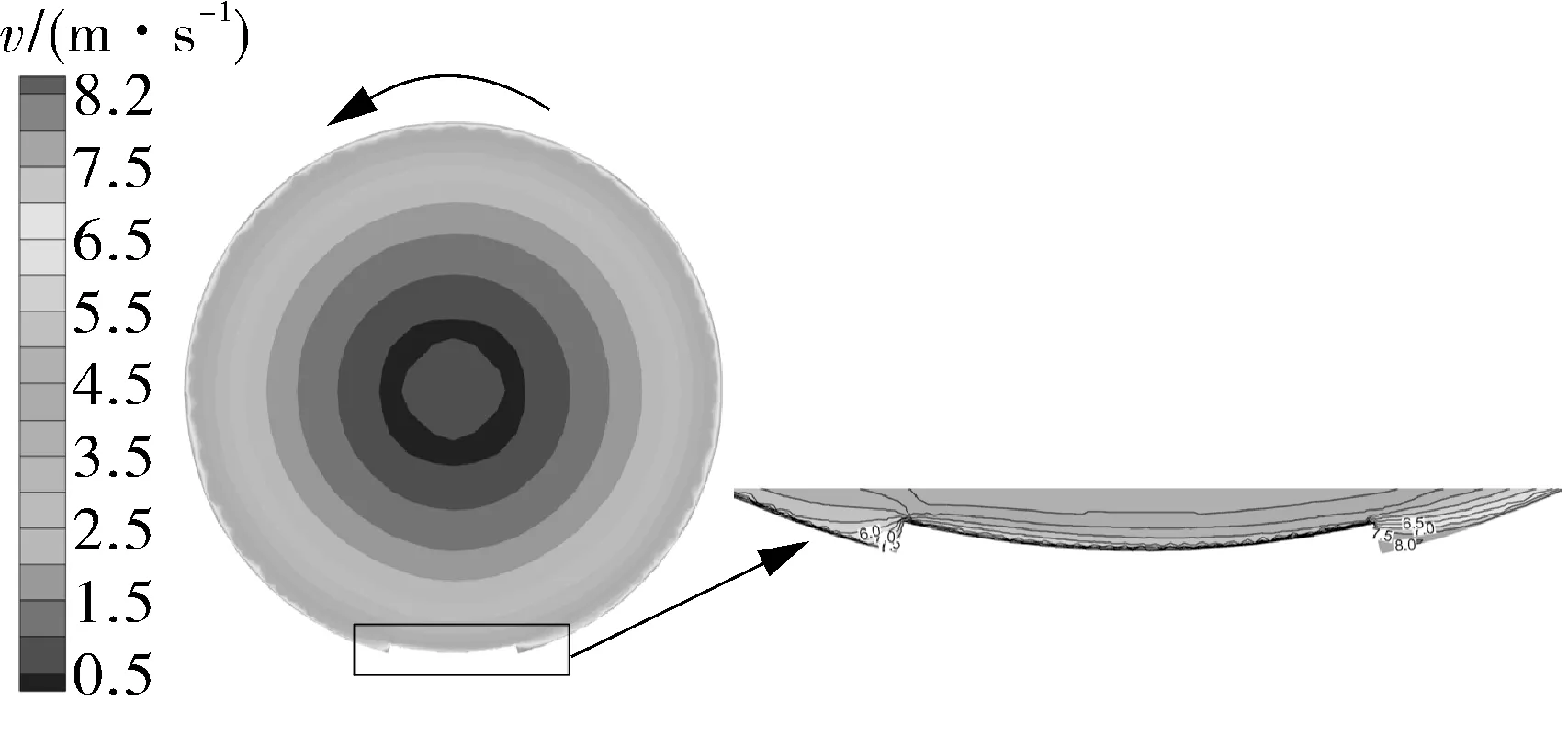
图5 微凸起圆筒的流场Fig.5 Flow field diagram of a slightly bulged cylinder

图6 整体磨损示意Fig.6 Schematic diagram of overall erosion

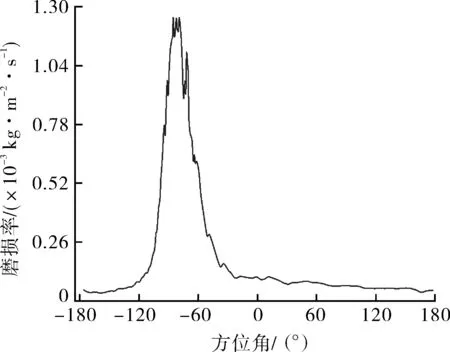
图7 空心轴内表面在微凸起进料侧不同方位角的磨损率Fig.7 Erosion rate of the inner surface of the hollow shaft at different azimuths on the feed side of the slightly bulged location

2.1.2 处理量对圆筒内壁微凸起的磨损率的影响

为了放大显示磨损试件磨损位置，通过表面涂层法在磨损试件的表面依次喷涂黑、红、绿3层油漆。试验结果显示，磨损位置主要分布在磨损试件的底部且磨损试件边缘处的磨损分布较大，左侧进料口位置的磨损范围大于右侧范围。从数值模拟得到的磨损云图（图8）可以看到，磨损件的磨损位置主要分布在其迎风面底部，且磨损试件边缘处的磨损分布较大，仿真磨损的分布与试验结果比较吻合；同时显示磨损量随着处理量增加而增大，通过图9中不同处理量下试件的磨损量与模拟的试件磨损量比较表明，模拟得到的试件磨损量和试验的试件磨损量均在转速为1 200 r/min、入口流速为1.37～2.74 m3/h时呈上升趋势且误差不超过10%，具有良好的一致性。因此，仿真方法和仿真结果的可靠性得到了证明。

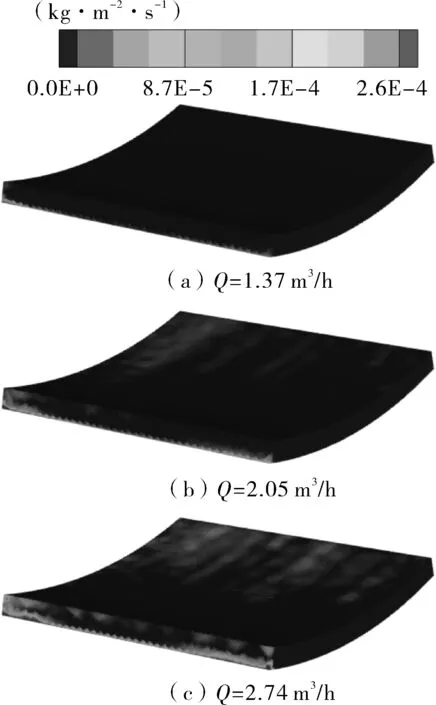
图8 不同处理量下微凸起壁面的磨损云图Fig.8 Erosion cloud diagram of the slightly bulged wall surface at different throughputs

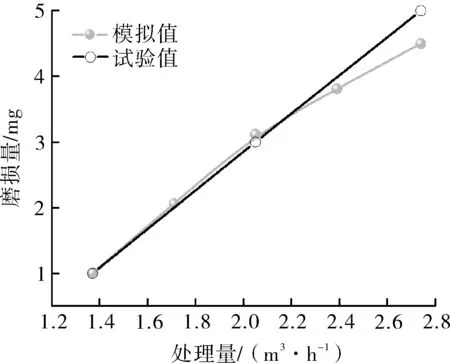
图9 不同处理量下试验试件磨损量与模拟磨损量的比较Fig.9 Comparison of erosion amount of test specimens with simulated erosion amount at different throughputs

处理量决定入口速度的大小，处理量越大，入口速度越大。分别取入口速度为1，1.5，2 m/s，及处理量分别为1.37，2.05，2.74 m3/h来研究处理量对壁面磨损的影响。从图8中可以看出，螺旋空心轴微凸起处的主要磨损部位发生在微凸起壁面的迎流面与壁面的交界处，壁面磨损的速率随着处理量的增大而增大。

图10显示微凸起处的磨损部位在轴向位置上没有发生较明显的改变，最大磨损率发生在轴向0～5 mm之间。处理量从1.37 m3/h增加到2.05 m3/h，微凸起壁面磨损率的峰值从6.2×10-4kg/（m2·s）增加到1.26×10-3kg/（m2·s）；处理量从2.05 m3/h增加到2.74 m3/h，微凸起壁面磨损率的峰值从1.26×10-3kg/（m2·s）增加到1.63×10-3kg/（m2·s）；随着处理量的增加，微凸起壁面轴向位置上壁面磨损率的增长速率也会相应加快。可见处理量对微凸起壁面磨损的影响很大，处理量越大入口速度越快，磨损率越高，微凸起壁面的磨损也将越严重。因为入口速度变大，颗粒惯性作用越强，颗粒受离心力大于液体越过壁面的升力，致使颗粒向微凸起的两端移动，移动过程受微凸起壁面与空心轴壁面形成的回流区的影响，使得颗粒不断撞击冲刷壁面，从而产生壁面磨损。处理量的增加，是导致壁面磨损加重的重要因素之一。

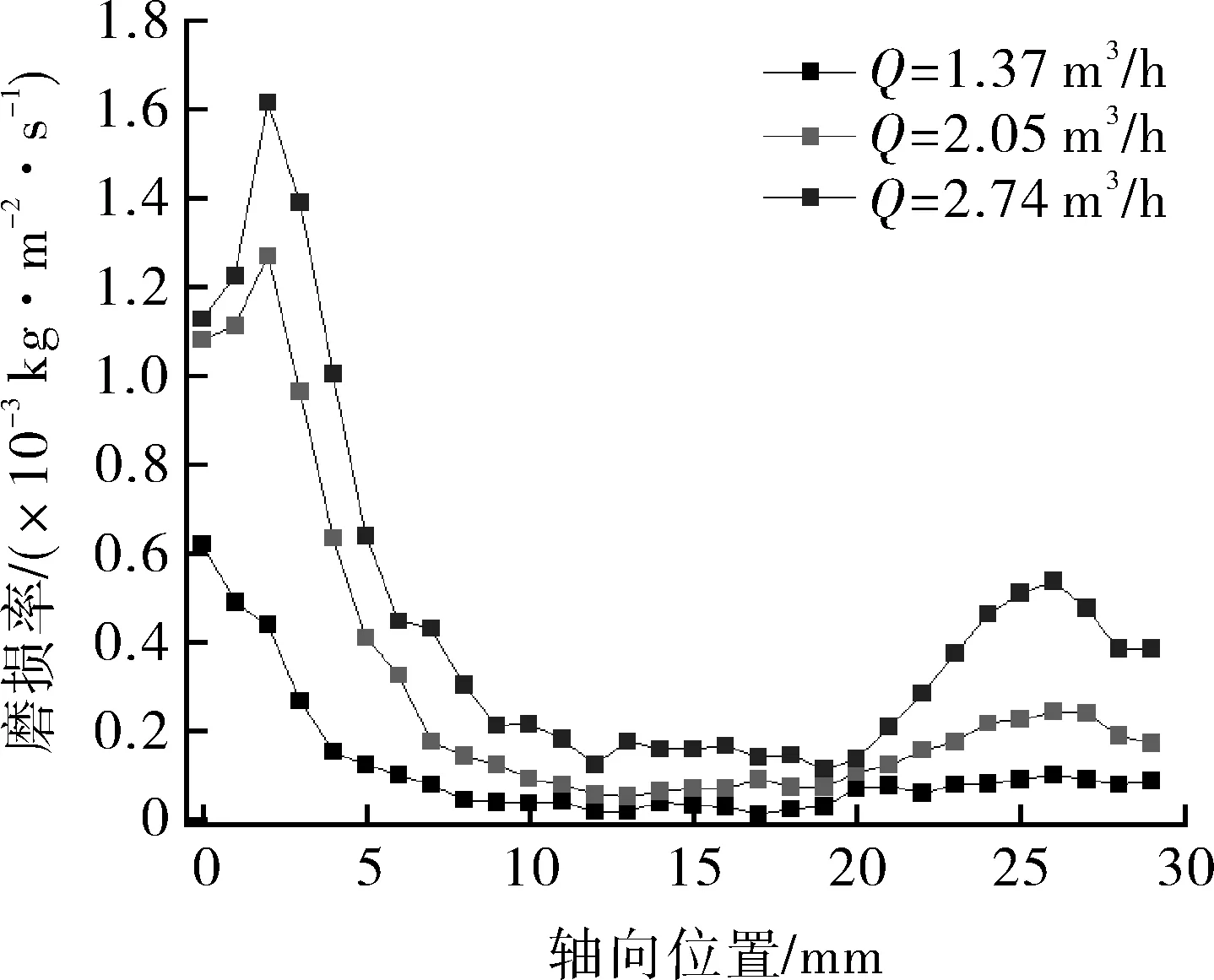
图10 不同处理量下微凸起的迎风面磨损率与轴向位置的关系Fig.10 Erosion rate of the windward side of the slightly bulged location at different throughputs as a function of axial position

2.2 螺旋空心轴内表面凹陷大小对凹陷内磨损的影响

由于材料局部低强度，或在加工、装配等过程中产生的工件表面局部凹陷，可能会导致局部磨损。

2.2.1 螺旋空心轴内表面有微凹陷时的流场及磨损

由图11可以看出，圆筒内部流体的速度总体上呈中心对称分布，反应了圆筒内部流体旋转的快慢，同时也决定了空心轴内部离心力的大小，对固体颗粒的运动产生很大的影响；速度的大小随着径向半径的增加逐渐增大。从缺陷处局部流体速度的等值线看出，缺陷处的流体速度大于空心轴内的速度，且在缺陷中心呈半圆分布，速度以缺陷中心呈对称分布，说明流体在此处形成了高速漩涡，缺陷处的大部分空间都被大于7.5 m/s的水流占据，可见缺陷处有更严重的磨损。

图11 缺陷截面处速度云图Fig11 Velocity cloud chart at defect section

在缺陷处的磨损主要集中在背流面的边角处，缺陷处的涡流可以将流动推向远离迎流面的方向，但是由于缺陷较小，所以流动主要推向了背流面且最大的磨损率达到4.31×10-4kg/（m2·s）。涡流可以以水垫的形式减轻撞击能量［16］。也可以像流体滚子轴承一样，减少壁面阻力，所以在迎流壁面处的磨损几乎为0。

从整体壁面上可见（见图12），无缺陷壁面的平均磨损率为2.5×10-5kg/（m2·s），缺陷处壁面的磨损率远大于无缺陷壁面的磨损率。所以在螺旋空心轴内壁面，如果材料的强度不均，在工作过程中材料强度低的壁面率先出现了缺陷，就会引起磨损集中现象，在该缺陷处的磨损率会剧增，直至磨穿。圆形凹陷处有比较严重的磨损集中现象。

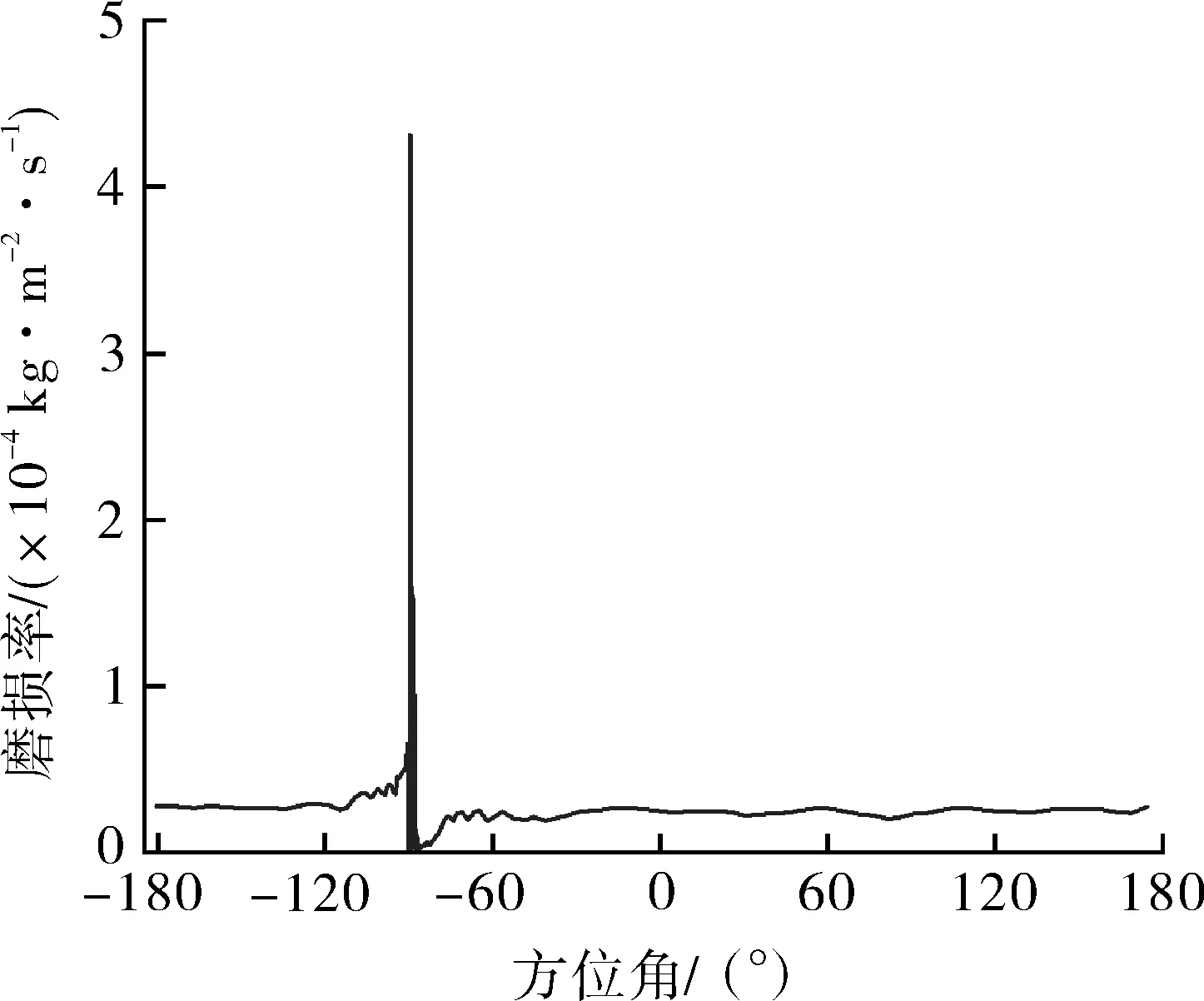
图12 圆筒内表面在凹陷的轴向位置处不同周向位置的磨损率Fig.12 Erosion rate of the inner surface of the cylinder at the axial position of the depression，at different circumferential positions

2.2.2 凹陷大小对圆筒内壁磨损率的影响

从图13中可知，在缺陷同一轴向位置处，缺陷处磨损率的峰值随着缺陷直径的增加而变大，但当方位角在-90°～-45°范围内，磨损率随着缺陷直径的增大而变小，这是由于缺陷处的涡流速度的降低导致沙粒的速度降低，使得缺陷底部的磨损率变低。在整体壁面处的磨损率降低是因为一部分沙粒在被迎流面涡流形成的水垫缓冲后，继续随着空心轴的旋转再回到主流中，且沙粒的相对速度随着直径的增大而减小，所以会出现缺陷迎流面附近磨损率几乎为0的现象。

图13 不同直径缺陷处截面不同方位角位置的磨损率Fig.13 Erosion rate curves for different azimuthal positions of the section at the positions of different diameter defects

3 结论

（1）微凸起处的磨损位置主要分布在其迎流面处的底部，且磨损率在其轴向位置上呈两端高中间低的分布，距离进料端位置的磨损率更高。

（2）随着处理量的增加，螺旋空心轴内壁面微凸起的最大磨损率也随之增加，当处理量达到2.74 m3/h时，磨损率峰值达到1.63×10-3kg/（m2·s）。微凸起壁面迎流面处产生的高速漩涡受入口速度的增加而进一步增强，带动颗粒对壁面进行高频率冲刷，使得流经区域磨损加剧。

（3）下凹缺陷的磨损区主要分布在其背流面，其分布主要受涡旋的影响；下凹缺陷磨损率峰值随着缺陷直径的增加而增加，缺陷直径从1 mm增加到3 mm时，磨损率峰值增加到4.31×10-4kg/（m2·s），迎流面的磨损率随着直径的增加而减小。

（4）壁面存在局部的凸起或下凹缺陷时，会产生局部区域的磨损率显著提高，特别对于下凹缺陷，磨损集中更加明显。